板翅式换热器锯齿型翅片参数的遗传算法优化研究

杨辉著,文键,童欣,李科,厉彦忠,王斯民

(1.西安交通大学能源与动力工程学院, 710049, 西安;2.西安交通大学化学工程与技术学院, 710049, 西安)



板翅式换热器锯齿型翅片参数的遗传算法优化研究

杨辉著1,文键1,童欣1,李科1,厉彦忠1,王斯民2

(1.西安交通大学能源与动力工程学院, 710049, 西安;2.西安交通大学化学工程与技术学院, 710049, 西安)

针对目前锯齿型板翅式换热器未能同时优化多参数,或者大多优化研究存在对经验关联式依赖的问题,提出了利用Kriging响应面来近似目标函数与设计变量之间的关系、应用遗传算法对锯齿型板翅式换热器翅片结构参数的优化方法。在维持翅片通道雷诺数为800时,把换热器的最大j因子、最小f因子和最大FTEF因子作为3个单目标函数,对翅片的翅片高度h、翅片间距s、翅片厚度t和翅片节距l进行了优化研究。研究结果表明:翅片高度h与翅片间距s对换热器综合性能FTEF因子呈正增长,而翅片厚度t和翅片节距l呈负增长;在翅片高度为9.5 mm、翅片间距为2.2 mm、翅片厚度为0.1 mm和翅片节距为3 mm时,换热器性能最佳;结合Kriging响应面的遗传算法克服了传统优化方法对经验关联式的依赖。该研究结果可以指导锯齿型板翅式换热器的优化设计。

板翅式换热器;遗传算法;Kriging响应面;优化设计

板翅式换热器的基本结构是,在相邻两隔板之间放置的二次传热面构成狭窄的矩形流体通道,其传热与流动阻力性能主要决定于具有二次传热的翅片表面特性。作为紧凑式换热器的基本传热元件,此二次传热面可以扩大传热面积,提高传热效率,增强结构紧凑性,提升换热器强度及承压能力。根据不同的工艺,翅片的型式主要有平直翅片、多孔翅片、锯齿翅片、波纹翅片和百叶窗翅片[1]。其中,锯齿型翅片以其紧凑、高的可靠性及传热效率高等优点得到了广泛的应用,不过也存在流动阻力大的缺点。因此,对锯齿型板翅式换热器进行优化研究,对于提高其传热量和降低运行费用具有重大的意义。

目前,板翅式换热器的设计主要依据经验选择、多次验算和前人所得结果,通过简单的流动与传热理论计算,在满足设定的换热性能和阻力要求时,即可作为所参考的换热器形式和翅片类型,然而这样得到的换热器形式并不能保证是最佳的方案。遗传算法[2]的基本理论依据是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局搜索算法,在板翅式换热器优化研究中得到广泛的应用。文献[3-5]以板翅式换热器重量和效率为目标函数,文献[6]以板翅式换热器火积耗散最小为目标函数,文献[7]以板翅式换热器熵产数为目标,对换热器进行了单目标遗传算法的优化研究。此外,文献[8]以能量消耗与材料花费为目标函数,文献[9]以换热量与压力损失为目标函数,文献[10]以总换热量与系统全年运行总成本为目标函数,对板翅式换热器进行了多目标遗传算法的优化研究。然而,上述的优化方法基本上都需要依靠经典关联式计算翅片的传热与阻力性能。文献[11-19]通过实验或数值研究的方法,提出了锯齿型翅片表面特性的关联式,但是这些关联式的工质都是空气,将其应用于大Pr为工质的情况,存在很大误差。目前,锯齿型板翅式换热器还严重缺乏以大Pr为工质的经验关联式。

本文以锯齿型板翅式换热器为研究对象,首先以翅片高度、翅片间距、翅片厚度和翅片节距为优化参数进行数值研究,然后结合Kriging响应面技术,基于遗传算法,在维持翅片通道Re恒定时,以j因子、f因子和FTEF因子为目标函数,对换热器的翅片高度、翅片间距、翅片厚度和翅片节距进行了优化设计。

1 计算模型与数值方法

1.1 优化设计物理模型

图1为锯齿型板翅式换热器翅片结构参数轴测图,其中翅片参数包括翅片高度h、翅片间距s、翅片厚度t和翅片节距l。图2为换热器翅片的平面图,可知单周期翅片端部参与换热的面积为Aend=2t(h-t)+t(s-2t),所以本文定义的当量直径[19]为

(1)

针对目前锯齿型板翅式换热器主要使用的翅片参数范围,此次选取的翅片优化范围是:h为4.7～9.5 mm,s为1.4～3 mm,t为0.1～0.5 mm,l为3～9 mm。

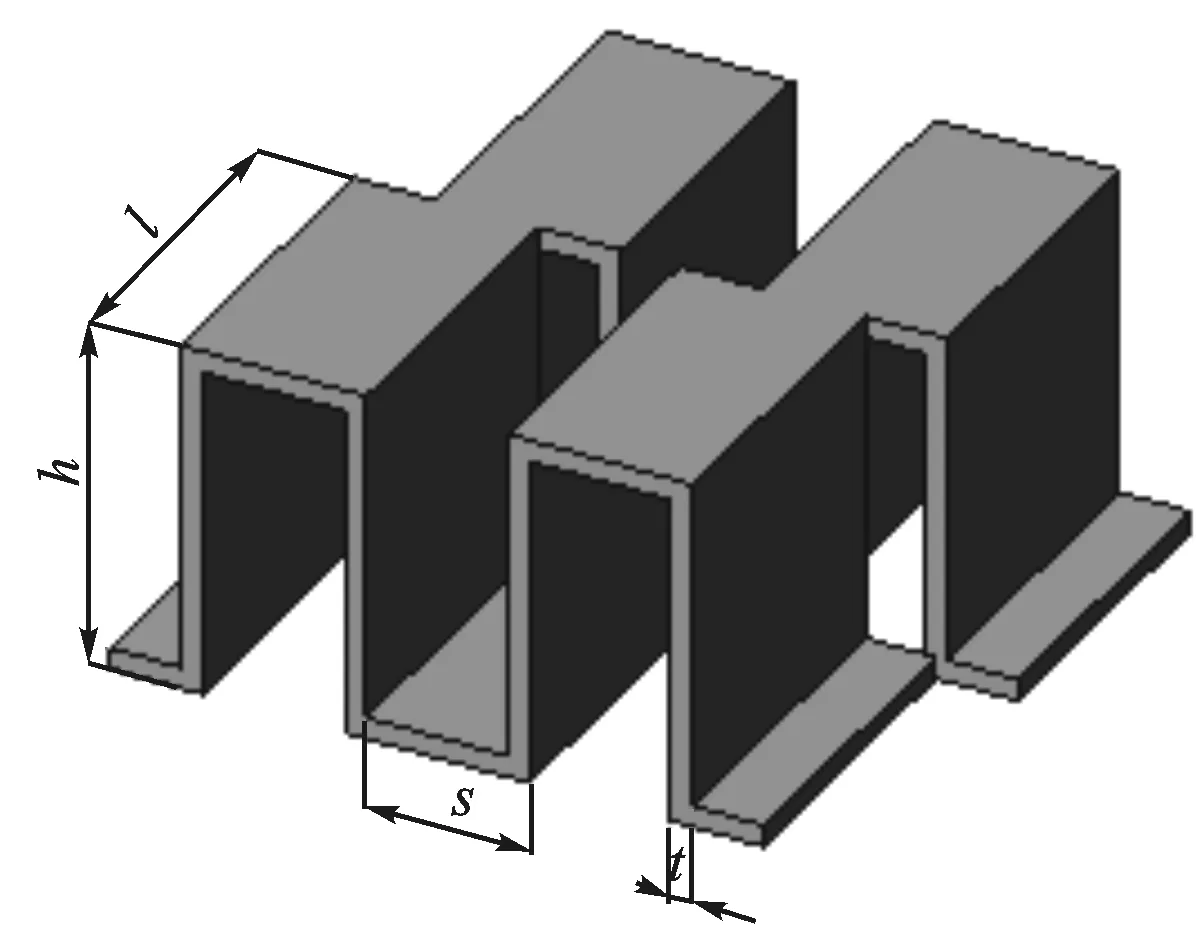
图1 锯齿型板翅式换热器翅片结构参数的轴测图

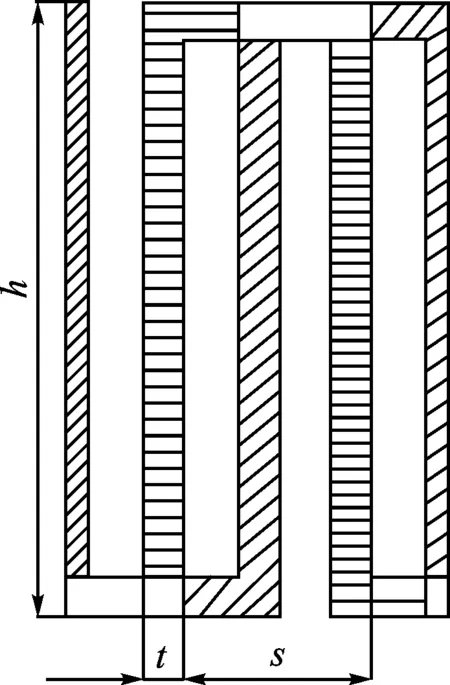
图2 锯齿型板翅式换热器翅片的平面图

1.2 基本方程及数值方法

本文的基本方程包括质量、动量以及能量方程。连续性方程为

(2)

动量方程为

(3)

能量方程为

(4)

模拟计算时,入口为质量流量边界条件,其对应的翅片通道Re维持为800,入口温度为300 K;出口为压力出口;假定上下隔板被充足的饱和蒸汽加热,即设定隔板表面为定壁温(373.15 K);侧面为周期边界条件;流固接触面为默认的耦合边界条件。板翅式换热器材料为铝,且忽略与外界的辐射与对流传热。通道流体为空气,其物性假定为常物性。压力-速度耦合采用SIMPLE算法,动量及能量方程使用二阶迎风格式。能量方程的计算残差为1×10-10,其他参数的残差为1×10-6。

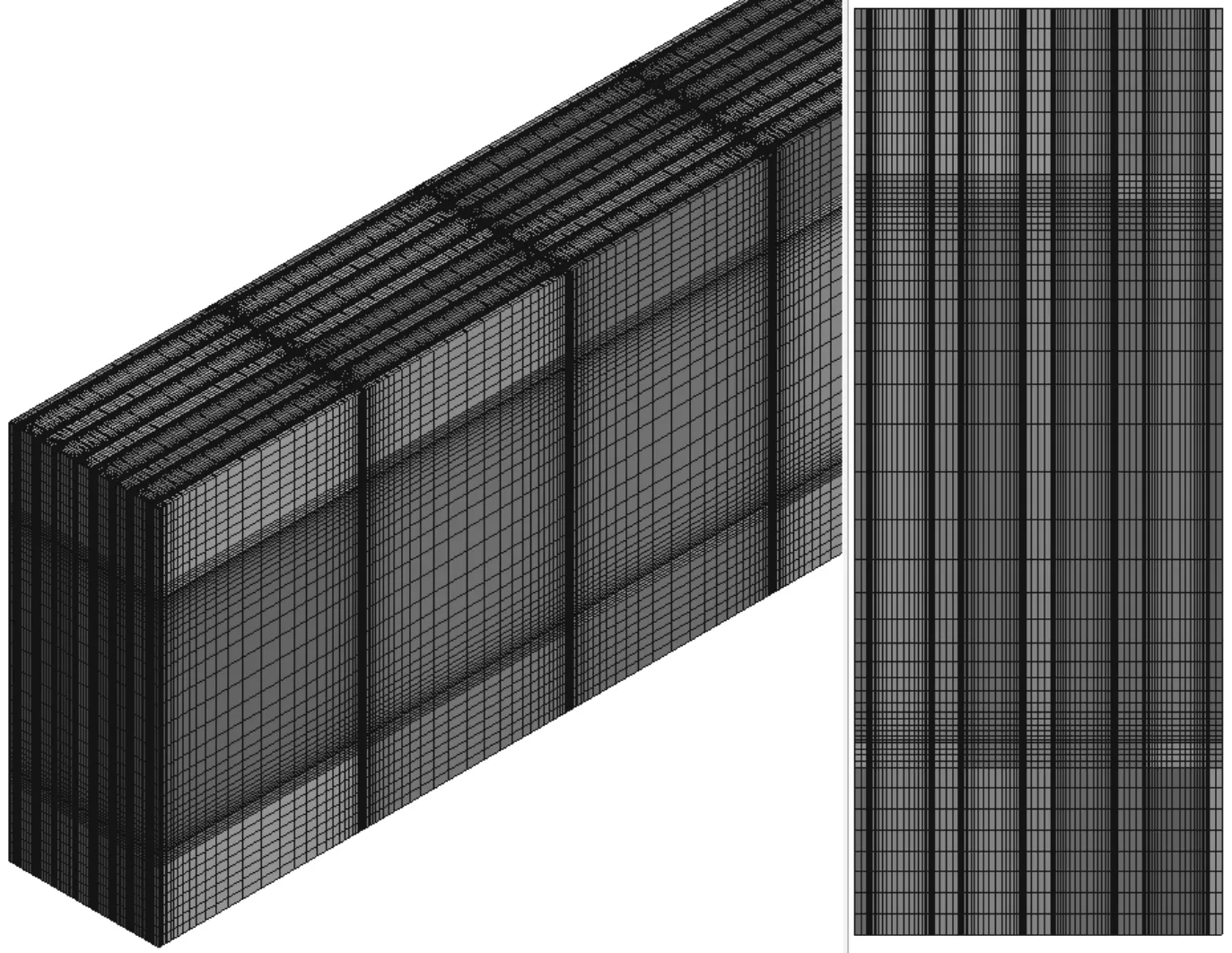
图3 锯齿型翅片网格示意图

计算模型的网格由mesh模块生产,全部采用结构化网格,同时对壁面划分了边界层网格及局部加密处理,板翅式换热器网格如图3所示。同时,为了保证计算结果的准确,对生成的网格进行了独立性验证。图4为对应无量纲y+为1、1.5、2、3、4和5的6组71JC2203翅片的网格无关性验证图。由图可知,在网格数增加到3 703 700后,换热器j因子和f因子变化都小于1%,考虑到计算的精度和缩短计算时间,选择网格为3 703 700。本文所有的锯齿型板翅式换热器的网格单元数为2 410 260～4 102 134。

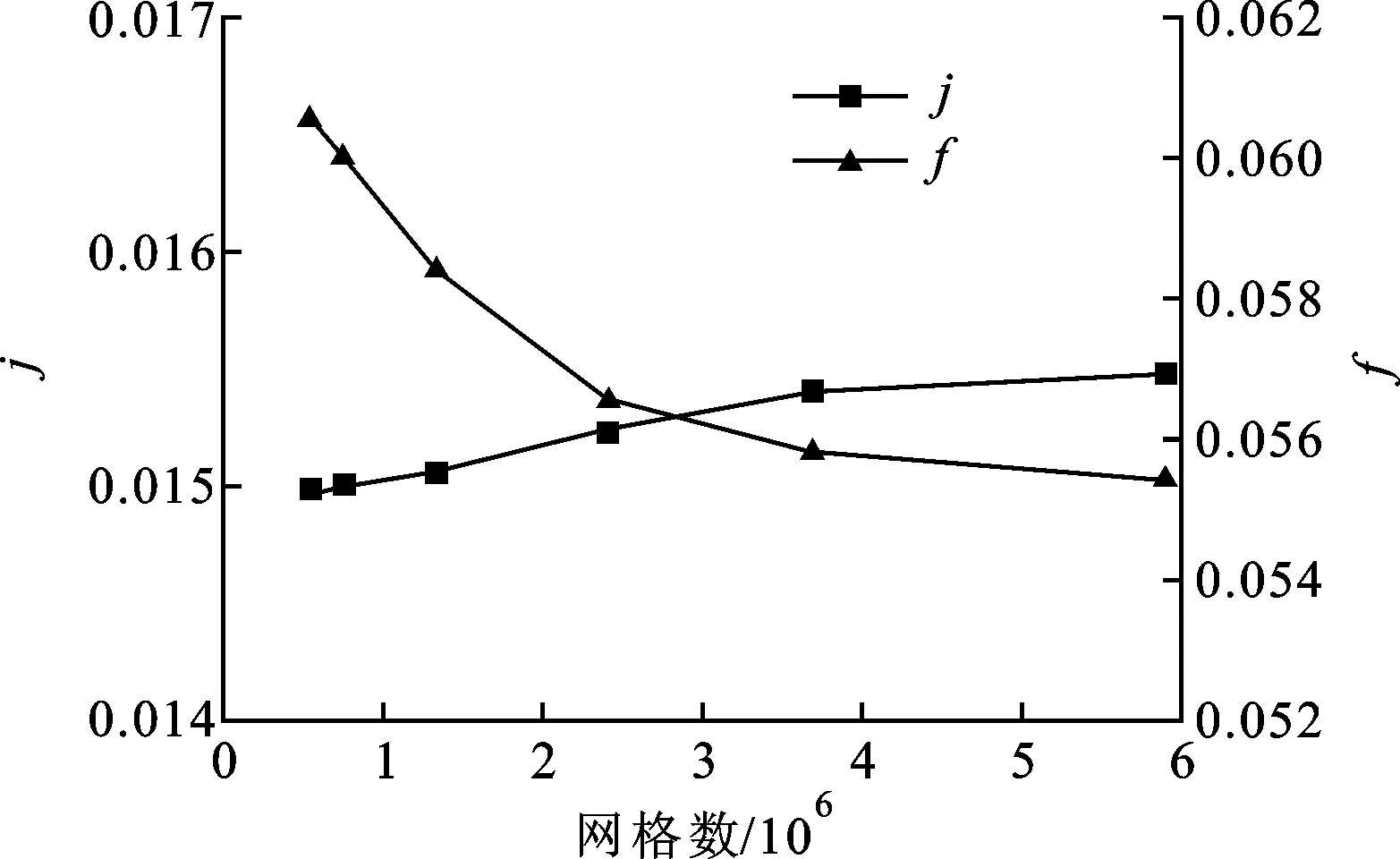
图4 71JC2203翅片的网格无关性验证

1.3 数值模拟有效性的验证

为了验证数值模拟的正确性,将模拟计算值与文献[10]锯齿型翅片的实验值进行对比,结果如图5所示,其中翅片型号为95JC1803。由图可知,j因子和f因子的数值结果与实验数据吻合较好。j因子数值结果与实验值的均方根误差为8.56%,而f因子数值结果与实验值的均方根误差为7.91%。由文献[10]得知,j因子及f因子存在5%的实验系统误差,因此可认为数值模拟结果是正确的。

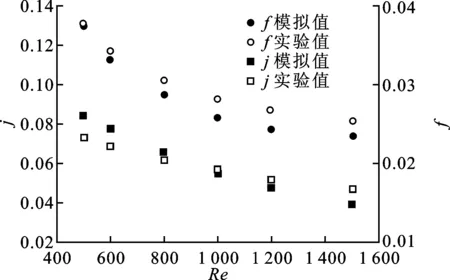
图5 数值模拟与实验结果的对比

2 优化研究

2.1 优化原理

图6为遗传算法的优化过程。优化过程包括初始试验设计、构造响应面和优化目标。在试验设计的选择中采用具有试验次数少、精度高、预测性好的中心组合设计。基于统计设计的先进优化方式,善于体现影响因素之间的交互作用程度,可以评估因素的非线性影响。响应面方法是指构造源模型的响应面,以解决源模型的设计或分析等问题的近似方法。这种利用响应面来近似目标函数与设计变量之间的关系,代替源函数进行估值,可以大大减少源函数的估值次数[20],克服了传统的全局优化方法对源函数的估值次数多、效率低的问题。Kriging方法是一种通过已知点来预测未知观察点的插值方法,其利用方差的变化来表达空间的变化,可以保证由空间分布得到的预测值的误差最小[21]。Kriging差值方法表示为Z(x)=f(x)+g(x),其中f(x)为二阶多项式方程(决定了模型了的全局行为),g(x)为扰动项(决定了模型的局部行为)。Kriging响应面可以同时提供目标点处的预测值和预测误差,保证响应面通过所有的样本点,使全局优化算法具有良好的全局性和局部性。最后,利用Kriging构造的响应面,通过遗传算法优化目标函数。这种基于响应面技术的遗传算法的优化研究,是利用响应面创建的输入、输出函数,而非传统的经验关联式,所以在处理无经验关联式,或者经验关联式不够准确的情况非常有效。不过这种方法得到的优化解是近似的,需要对优化解进行验证。

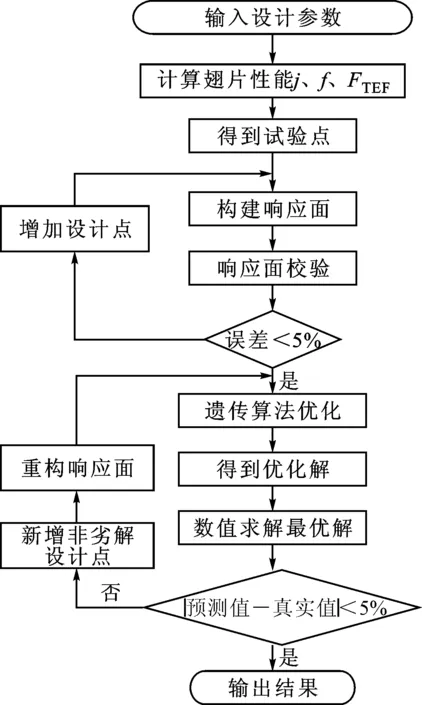
图6 遗传算法的优化过程

2.2 数据处理

计算Nu及j因子

(5)

(6)

(7)

(8)

(9)

式中:u为通道速度;D为当量直径;h为传热系数;m为流体质量流量;cp为比定压热容;T为温度;Δtm为对数平均温差;λ为导热系数;μ为动力黏度;下标in、out分别表示进、出口。

计算摩擦因子f

(10)

式中:Δp为压差;ρ为流质密度;L为翅片长度。

计算FTEF因子

(11)

3 结果分析与讨论

3.1 数值结果与经验关联式的对比

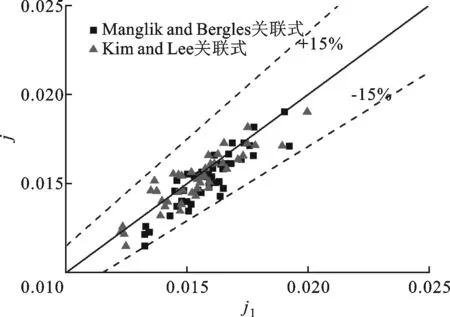
(a)j因子

采用中心组合设计的方法,均匀分配了50个设计点。为了验证数值结果的正确性,将本文结果与Mangles & Bergles关联式和Kim & Lee关联式进行了对比,结果如图7所示,其中横坐标为关联式的计算结果j1、f1,纵坐标为本文结果。由图7a可知,Mangles & Bergles和Kim & Lee关联式的j因子与数值结果吻合的较好。Mangles & Bergles关联式的误差范围在±15%,均方根误差为6.0%,而Kim & Lee关联式的误差范围在±10%,均方根误差为4.7%。由图7b可知,Mangles & Bergles和Kim & Lee关联式的f因子与本文结果的误差基本维持在±20%之间,不过也存在少量Mangles & Bergles关联式的误差达到25%。Mangles & Bergles关联式与本文结果的均方根误差为18.7%,而Kim & Lee关联式的均方根误差为15.4%。产生误差的原因可能是f因子与翅片当量直径成正比,j因子与当量直径无关。Mangles & Bergles和Kim & Lee关联式定义的当量直径比本文的大,因此本文结果的f因子必然比经验关联式的值小。此外,数值模拟忽略翅片表面的粗糙度,也导致f因子偏小。由于经验关联式本身也存在±20%误差,可认为本文数值模拟结果是准确的。

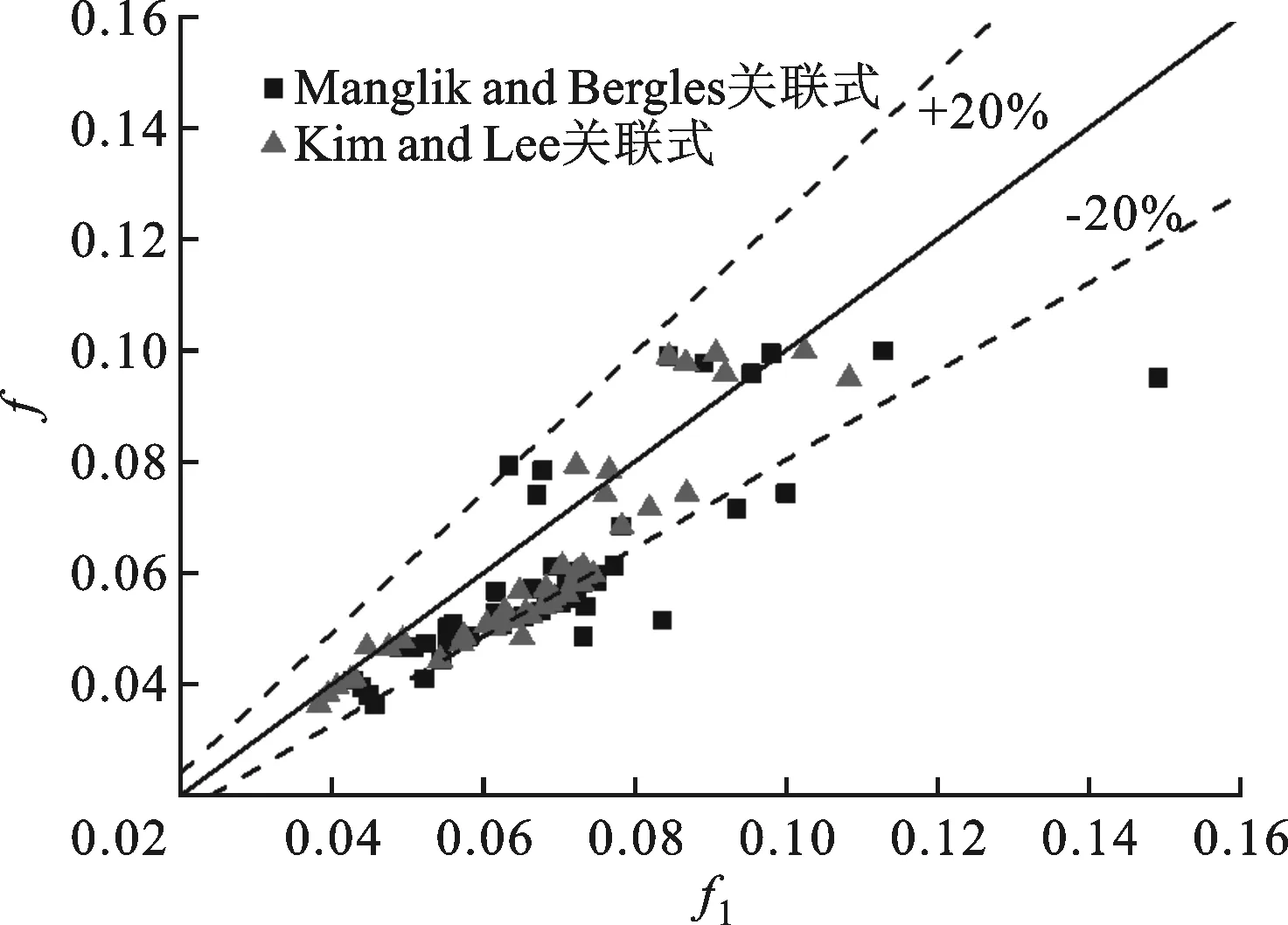
(b)f因子图7 本文结果与经验关联式结果的对比

3.2 翅片参数对换热性能的影响

3.2.1 翅片高度h的影响
图8为s=2.2 mm、t=0.3 mm、l=6 mm时,不同翅片高度h对j因子、f因子及FTEF因子的影响。由图8可知,随着h的增加,j因子、f因子及FTEF因子都逐渐增加,其中j因子增加23.8%,f因子增加14.3%,FTEF因子增加18.4%。随着h增加,翅片二次传热面积显著增加,增大了流体与翅片的换热面积,强化了传热。虽然h增加使翅片通道流速减小,但是在维持通道Re一定时,流道内的质量流量是增加的,最终导致j因子、f因子都所有增加。增加h有利于强化换热,所以在满足允许的压降下,应适当增加翅片高度。

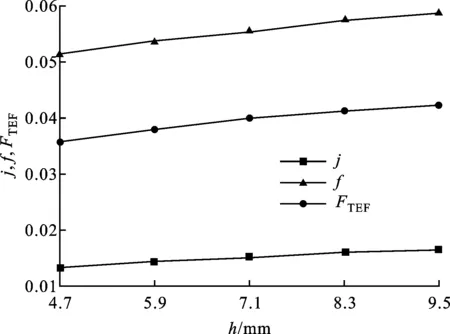
图8 翅片高度h对换热性能的影响

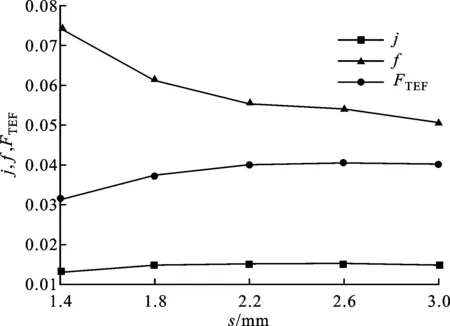
图9 翅片间距s对换热性能的影响

3.2.2 翅片间距s的影响
图9为h=7.1 mm、t=0.3 mm、l=6 mm时,不同s对j因子、f因子及FTEF因子的影响。由图9可知,随着s的增加,j因子和FTEF因子先有所增加后趋于稳定,而f因子先快速减小后变缓,其中j因子增加16%,f因子降低47%,FTEF因子增加27.9%。随着s增加,翅片一次表面和通道内的质量流量都增加,强化了传热,使j因子增加。翅片通道内流速快速下降使f因子显著下降,同时通道内流量增加又减缓了f因子的下降。低翅片间距使通道压降变大,翅片性能变差,应该适当设计大的翅片间距。

3.2.3 翅片厚度t的影响
图10为h=7.1 mm、s=2.2 mm、l=6 mm时,不同t对j因子、f因子及FTEF因子的影响。由图10可知,随着t的增加,j因子几乎不变,FTEF因子逐渐减小,而f因子迅速增加,其中,FTEF因子减小27.8%,f因子增加88.6%。翅片厚度增加导致通道流通面积减小,流速快速增加,引起f因子的显著提高。同时,虽然流速增加有利于换热,但是通道质量流量和换热面积都减小,结果j因子几乎不变。翅片厚度对换热器的压降具有特别明显的影响,在低压板翅式换热器的设计中应该选择薄翅片,而高压翅片应该要特别注意验算允许的压降。

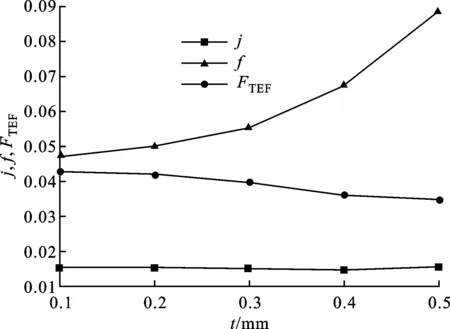
图10 翅片厚度t对换热性能的影响

3.2.4 翅片节距l的影响
图11为h=7.1 mm、s=2.2 mm、t=6 mm时,不同l对j因子、f因子及FTEF因子的影响。由图11可知,随着l的增加,j因子、f因子、FTEF因子都降低,其中j因子降低30.1%,f因子降低41.5%,FTEF因子降低15.9%。翅片节距的增加,减小了对流体的扰动,j因子和f因子都减小。FTEF因子的减小,说明应该选择短的翅片间距。

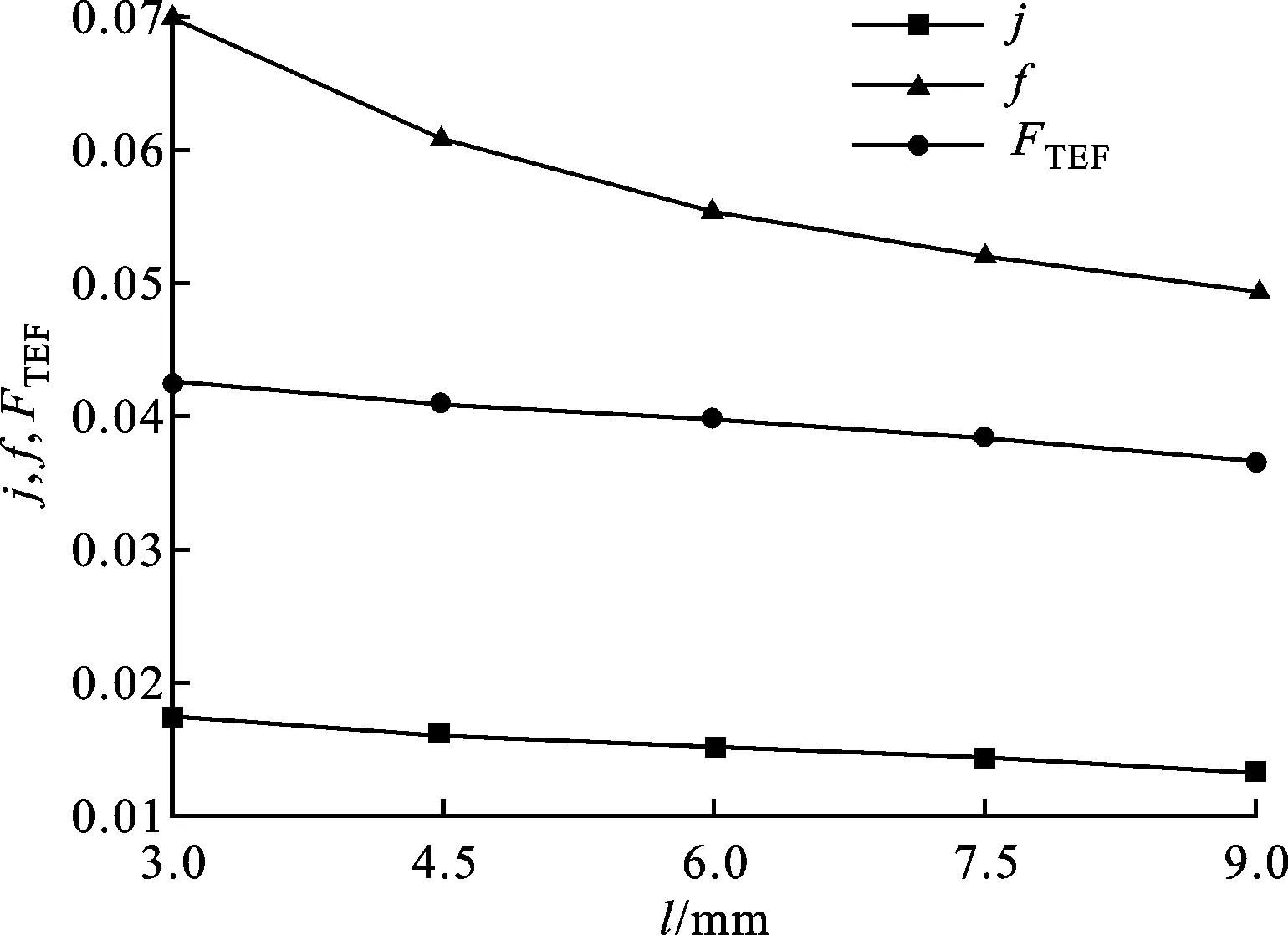
图11 翅片节距l对换热性能的影响

3.3 翅片参数的敏感性

图12为翅片参数对于换热器性能的敏感性。由图可以发现,h和s对j因子呈正增长,而t和l对j因子呈负增长,且h和l对j因子的影响较大。h和t对f因子呈正增长,而s和l对f因子呈负增长。当t较大时,将会导致通道压降快速增加,引起较高的运行费用。h和s对FTEF因子呈正增长,而t和l对FTEF因子呈负增长。这种从定性到定量分析翅片参数对换热器性能影响的方法,对于指导翅片参数的选择、提高板翅式换热器性能具有重大的意义。

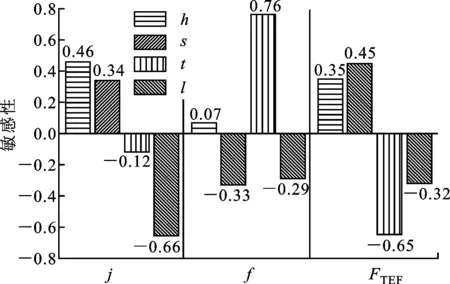
图12 翅片参数对换热器性能的敏感性

3.4 优化结果

图13为以换热器FTEF因子最大为目标函数的优化过程。从图可知,在优化初始阶段个体差异较大,较差的目标值被淘汰,目标函数值变化较明显,随后目标函数值变化幅度逐渐减弱,

最终趋于一个

稳定值。表1为维持入口Re=800时,以最大j因子、FTEF因子及最小f因子为目标的优化结果。由于基于响应面的优化方法,优化结果是由遗传算法得到的近似解,所以为了验证结果的准确性,对优化结果与通过CFD真实求解的结果进行了对比。由表1可知,优化值与CFD真实求解的值误差很小,都在±10%以内,说明了利用Kriging响应面技术并应用遗传算法可以有效地优化设计板翅式换热器。在维持Re恒定时,得到最大j因子和最大FTEF因子的翅片结构参数非常相似,即采用薄的翅片厚度、高的翅片高度、短的翅片节距和适当大的翅片间距。为了减小翅片阻力,应该采用薄的翅片厚度、低的翅片高度、大的翅片间距和适当大的翅片节距。考虑到实际生产,在翅片通道Re=800时,得到锯齿型板翅式换热器性能最好的翅片参数为h=9.5 mm、s=2.2 mm、t=0.1 mm和l=3 mm。

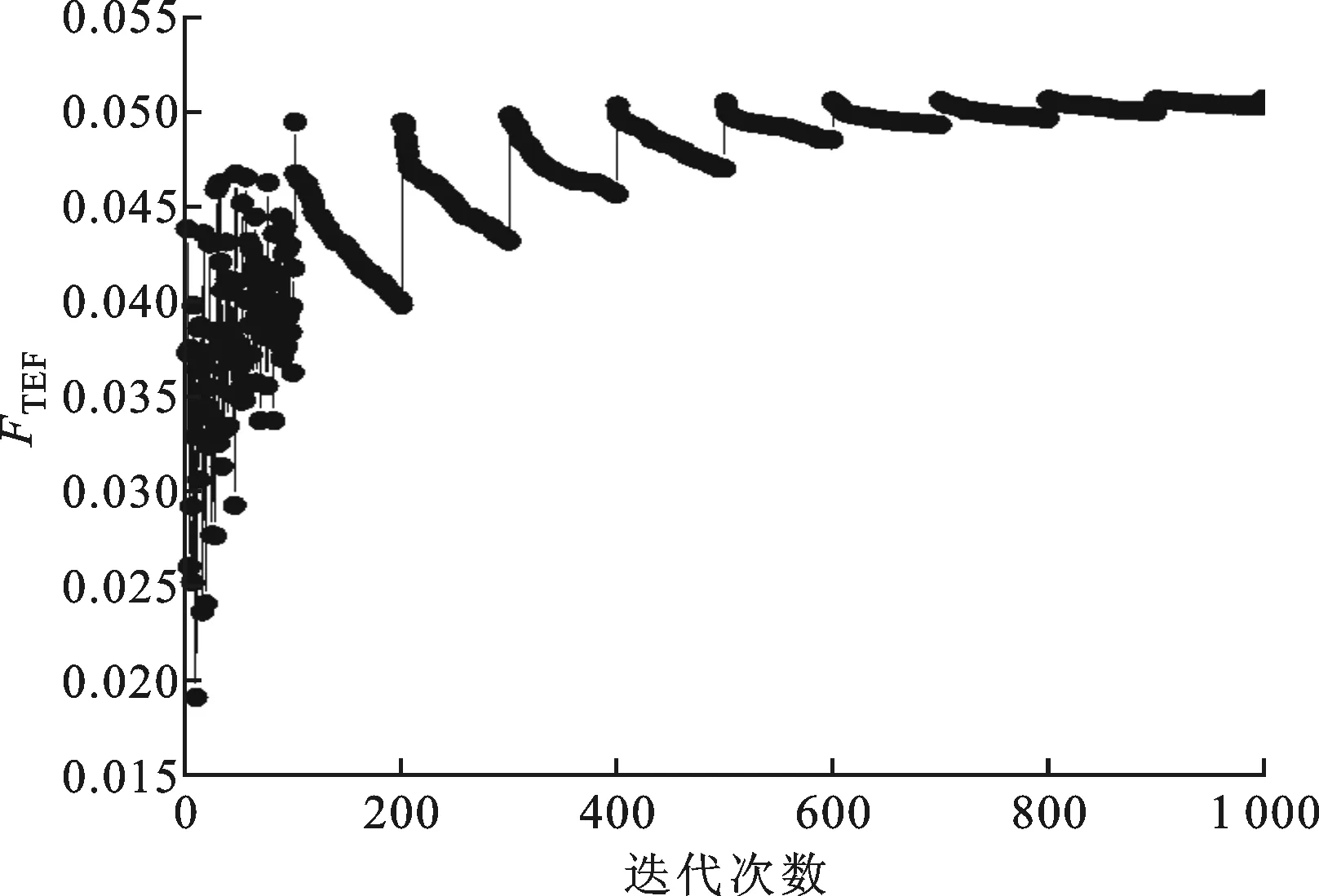
图13 以FTEF最大为目标函数的优化过程

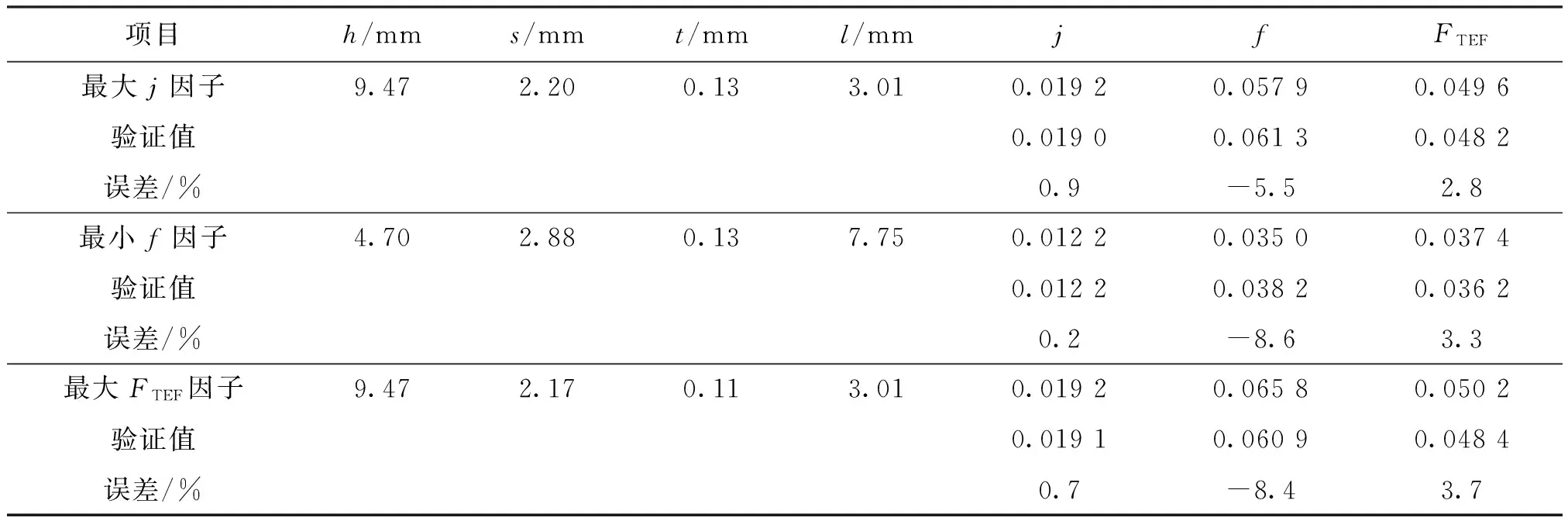
项目h/mms/mmt/mml/mmjfFTEF最大j因子9.472.200.133.010.01920.05790.0496验证值0.01900.06130.0482误差/%0.9-5.52.8最小f因子4.702.880.137.750.01220.03500.0374验证值0.01220.03820.0362误差/%0.2-8.63.3最大FTEF因子9.472.170.113.010.01920.06580.0502验证值0.01910.06090.0484误差/%0.7-8.43.7

4 结 论

利用Kriging响应面技术,以最大j因子、FTEF因子和最小f因子为目标函数,应用遗传算法优化设计了锯齿型板翅式换热器的翅片参数,可得出以下结论。

(1)锯齿型翅片高度h与翅片间距s对换热器综合性能FTEF因子呈正增长,而翅片厚度t和翅片节距l呈负增长,其中翅片高度的影响为35%,翅片间距为45%,翅片厚度为-65%和翅片节距为-32%。

(2)在翅片通道Re=800时,锯齿型板翅式换热器的翅片高度h=9.5 mm、翅片间距s=2.2 mm、翅片厚度t=0.1 mm和翅片节距l=3 mm时性能最佳。

(3)基于Kriging响应面技术,应用遗传算法可以有效地优化设计板翅式换热器,并且该方法克服了传统优化方法对于经验关联式的依赖,对于解决缺少经验关联式的复杂问题非常有效。

[1] SHAH R K, WEBB L. Compact and enhanced heat exchangers: heat exchangers theory and practice [M]. Washington, DC, USA: Hemisphere, 1983: 425-468.

[2] HOLLAND J H. Outline for a logical theory of adaptive systems [J]. Journal of the Association for Computing Machinery, 1962, 9(3): 297-314.

[3] PENG H, LING X. Optimal design approach for the plate-fin heat exchangers using neural networks cooperated with genetic algorithms [J]. Appl Therm Eng 2008, 28(5/6): 642-650.

[4] XIE G N, SUNDEN B, WANG Q W. Optimization of compact heat exchangers by a genetic algorithm [J]. Appl Therm Eng, 2008, 28(8/9): 895-906.

[5] 谢公南, 王秋旺. 遗传算法在板翅式换热器尺寸优化中的应用 [J]. 中国电机工程学报, 2006, 26(7): 53-57. XIE Gongnan, WANG Qiuwang. Geometrical optimization design of plate-fin heat exchanger using genetic algorithm [J]. Proceedings of the CSEE, 2006, 26(7): 53-57.

[6] 郭江峰, 许明田, 程林. 基于耗散数最小的板翅式换热器优化设计 [J]. 工程热物理学报, 2011, 32(5): 827-831. GUO Jiangfeng, XU Mingtian, CHENG Lin. Optimization design of plate-fin heat exchanger based on entransy dissipation number minimization [J]. Journal of Engineering Thermophysics, 2011, 32(5): 827-831.

[7] MISHRA M, DAS P K, SUNIL S. Second law based optimization of crossflow plate-fin heat exchanger design using genetic algorithm [J]. Appl Therm Eng, 2009, 29(14): 2983-2989.

[8] GHOLAP A K, KHAN J A. Design and multi-objective optimization of heat exchangers for refrigerators [J]. Applied Energy, 2007, 84(12): 1226-1239.

[9] HILBERT R, JANIGA G, BARON R, et al. Multi-objective shape optimization of a heat exchanger using parallel genetic algorithms [J]. Int J of Heat Mass

Transfer, 2006, 49(15/16): 2567-2577.

[10]NAJAFI H, NAJAFI B, HOSEINPOORI P. Energy and cost optimization of a plate and fin heat exchanger using genetic algorithm [J]. Appl Therm Eng, 2011, 31(10): 1839-1847.

[11]KAYS W M, LONDON A L. Compact heat exchanger [M]. 2nd ed. New York, USA: McGraw-Hill, 1964: 97-112.

[12]WIETING A R. Empirical correlations for heat transfer and flow friction characteristics of rectangular offset-fin plate-fin heat exchangers [J]. J Heat Transfer, 1975, 97(3): 488-490.

[13]JOSHI H M, WEBB R L. Heat transfer and friction in the offset-strip fin heat exchangers [J]. Int J of Heat Mass Transfer, 1987, 30(1): 69-84.

[14]MANSON S V. Correlations of heat transfer data and of friction data for interrupted plane fins staggered in successive rows, NACA tech note 2237 [R]. Washington, DC, USA: National Advisory Committee for Aeronautics, 1950.

[15]MOCHIZUKI S, YAGI Y, YANG W J. Transport phenomena in stacks of interrupted parallel-plate surfaces [J]. Exp Heat Transfer, 1987, 1(2): 127-140.

[16]DUBROVSKY E V, VASILIEV V Y. Enhancement of convective heat transfer in rectangular ducts of interrupted surfaces [J]. Int J of Heat Mass Transfer, 1988, 31(4): 807-818.

[17]MANGLIK R M, BERGLES A E. Heat transfer and pressure drop correlations for the rectangular offset strip fin compact heat exchanger [J]. Exp Therm Fluid Sci, 1995, 10(2): 171-180.

[18]KIM M S, LEE J, YOOK S J, et al. Correlations and optimization of a heat exchanger with offset-strip fins [J]. Int J of Heat Mass Transfer, 2011, 54(9/10): 2073-2079.

[19]YANG Y J, LI Y Z. General prediction of the thermal hydraulic performance for plate-fin heat exchanger with offset strip fins [J]. Int J of Heat Mass Transfer, 2014, 78(7): 860-870.

[20]WANG G G, SHAN S. Review of metamodeling techniques in support of engineering design optimization [J]. Journal of Mechanical Design, 2007, 129(4): 370-380.

[21]SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments [J]. Statistical Science, 1989, 4(4): 409-435.

(编辑 杜秀杰)

Optimization Design for Offset Fin in Plate Heat Exchanger with Genetic Algorithm

YANG Huizhu1,WEN Jian1,TONG Xin1,LI Ke1,LI Yanzhong1,WANG Simin2

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Chemical Engineering and Technology, Xi’an Jiaotong University, Xi’an 710049, China)

In the current optimization for plate fin heat exchanger with offset fins, simultaneous multi-parameter optimization is rarely considered, or researches usually depend on empirical relations. A strategy by genetic algorithm (GA) combined with Kriging response surface is proposed, where the Kriging response surface provides an approximate relationship between the objective function and design variables. The fin heighth, fin spaces, fin thicknesstand interrupted lengthjof offset fins are taken as four optimization parameters, while maximumjfactor, minimumffactor and maximumFTEFfactor as three single objective functions at Reynolds number of 800. The results show that the effects of the fin height and fin space on the overall performanceFTEFfactor are positive and the effects of the fin thickness and the interrupted length are negative; the heat exchanger performance reaches the optimum as fin heighth=9.5 mm, fin spaces=2.1 mm, fin thicknesst=0.1 mm and interrupted lengthl=3 mm; the genetic algorithm combined with Kriging response surface eliminates the dependence on empirical relations.

plate-fin heat exchanger; genetic algorithm; Kriging response surface; optimization design

2015-04-27。

杨辉著(1988—),男,博士生;王斯民(通信作者),男,副教授。

国家自然科学基金资助项目(51106119,81100707);中央高校基本科研业务费专项资金资助项目。

时间:2015-10-28

10.7652/xjtuxb201512015

TK124

A

0253-987X(2015)12-0090-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151028.1527.002.html