采用独立阈值的遥感影像变化检测方法
贾永红,谢志伟,张谦,杨刚
(1.武汉大学遥感信息工程学院, 430079, 武汉;2.武汉大学测绘遥感信息工程国家重点实验室, 430079, 武汉;3.华中科技大学自动化学院, 430074, 武汉;4.武汉大学资源与环境科学学院, 430079, 武汉)
采用独立阈值的遥感影像变化检测方法
贾永红1,2,谢志伟1,张谦3,杨刚4
(1.武汉大学遥感信息工程学院, 430079, 武汉;2.武汉大学测绘遥感信息工程国家重点实验室, 430079, 武汉;3.华中科技大学自动化学院, 430074, 武汉;4.武汉大学资源与环境科学学院, 430079, 武汉)
针对在多时相遥感影像变化检测中常规阈值确定方法无法获取小比例变化量区域准确变化阈值,并导致变化检测失败的问题,提出了采用独立阈值的遥感影像变化检测方法。通过多时相遥感影像多尺度分割获取像斑,采用变化向量分析法计算像斑差异度;从像斑差异度中自适应选择满足期望最大化算法和贝叶斯最小误差率理论获取准确阈值条件的训练样本;将训练样本导入独立阈值法确定变化阈值,利用变化阈值对像斑差异度进行二值分割获得影像变化的检测结果。实验结果表明,采用独立阈值的遥感影像变化检测方法能够获得更准确的变化阈值,在城郊变化检测中平均漏检率较全局阈值法和局部阈值法降低了9.6%和17.24%,在城区变化检测中平均正确率较全局阈值法和局部阈值法提高了51.27%和35.42%。
变化检测;小比例变化量区域;像斑;样本选择;期望最大化算法
遥感技术可以为地理国情监测提供重要技术支撑,多时相遥感数据变化检测是地理国情实现动态监测的关键。非监督法变化检测因其在效率和精度上的优势,在实际生产中得到更多重视[1]。
非监督法变化检测通过变化阈值对差异影像进行二值分割获取变化检测结果。常用的二值分割算法可分为全局阈值法和局部阈值法两类。文献[2]提出了基于期望最大化(expectation maximization,EM)算法和贝叶斯最小误差率理论的全局阈值法变化检测,该方法将整幅差异影像的灰度直方图作为全局信息,通过对其分析并自动计算变化阈值,在多时相遥感影像变化检测中得到了广泛应用[3-5]。然而,采用基于EM算法和贝叶斯最小误差率理论获取变化阈值需要满足如下条件:若将检测区域内变化区域与未变化区域的面积比例定义为变化量比例,当检测区域为大比例变化量区域时,可以有效地获得准确变化阈值;当检测区域为小比例变化量区域时,则不能获得准确的变化阈值[6]。因此,采用全局阈值法的变化检测无法对小比例变化量区域进行有效变化检测。局部阈值法变化检测[7-8]通过格网分块将2个时相的遥感影像均划分为重叠的影像块,再采用全局阈值法分别计算每个影像块的变化阈值,若对应的2个时相影像块为小比例变化量区域则无法获得该影像块区域的准确变化阈值。在地理国情监测中,使用的多时相遥感影像采集时间相近,且数据尺寸较大,导致检测区域内常常只有少量土地覆盖发生变化,即为小比例变化量区域,全局阈值法或局部阈值法均不能得到准确变化阈值,导致上述方法无法在地理国情监测中得到应用。
由于面向对象的变化检测在多时相高分辨率遥感影像变化检测中的效果优于像素级变化检测[9],本文亦将影像对象作为基本处理单元,并将影像对象称为像斑。
本文在上述研究的基础上,提出采用独立阈值的遥感影像变化检测方法,通过多尺度影像分割获取像斑,采用变化向量分析法(change vector analysis,CVA)[4]计算像斑差异度,然后自适应选择训练样本,结合EM算法和贝叶斯最小误差率理论的阈值计算方法,通过独立阈值法确定变化阈值,最后利用变化阈值对差异影像进行二值分割获取变化检测结果。本文选择城郊和城区两种土地覆盖类型实验数据来验证本文方法的有效性。
1 影像预处理
遥感影像几何配准是实现多时相遥感影像变化检测的关键前提,本文采用文献[10]的影像配准方法对2个时相遥感影像进行配准。通过分形网络演化算法对配准后的多时相遥感影像进行多尺度分割,获取同时具备光谱和形状同质性的像斑。分割尺度参数、紧致度、形状因子是影响分割结果的3个因素。分割尺度参数用来控制观测地物的细微程度,主要依靠使用者的经验知识利用启发式的方法确定;紧致度表征对象的规则程度,紧致度过小会使分割后的像斑不完整;形状因子为参与分割的形状异质度的权重,适当的形状因子能够减少像斑的边界破碎程度[11]。
本文采用文献[12]的多时相影像多尺度分割方法,首先将配准后的2个时相的遥感影像进行叠加;然后对叠加后的多维影像进行多尺度分割;最后将分割结果拆分成叠加前的2个时相影像多波段形式,由此分别得到2个时相影像的分割结果。本文方法综合考虑了2个时相影像的光谱和空间信息,保证了不同时相相同影像位置所对应的像斑包含的像元相同,并在各自的时相中具有光谱、空间同质性,利于进行像斑级的比较和分析。
2 独立阈值法变化检测
2.1 自适应样本选择
针对小比例变化量区域进行变化检测,通过自适应样本选择的方法选择整幅影像中具有大比例变化量的局部区域作为训练样本。自适应样本选择方法具体如下。
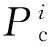
(1)
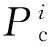
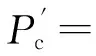
(2)
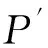
2.2 基于EM算法和贝叶斯最小误差率理论的阈值确定
采用贝叶斯最小误差率理论计算变化阈值需要以下变量:类别数、每个类别的先验概率、每个类别的条件概率密度函数。假设作为样本的像斑差异度集合为D={d1,…,dk},k≤m,m为像斑数量。采用贝叶斯最小误差率理论将集合D分为变化类wc和未变化类wn,则D的分类问题转为估计条件概率密度函数p(dk|wc)和p(dk|wn)的参数,以及先验概率p(wc)和p(wn),且p(wc)+p(wn)=1。假设p(dk|wc)和p(dk|wn)均服从高斯分布,则有
(3)
式中:l∈{c,n};μl、δl为变化类像斑和未变化类像斑的均值和标准差。D中像斑差异度近似满足2个高斯分布组成的混合高斯分布
p(dk)=p(wc)p(dk|wc)+p(wn)p(dk|wn)
(4)
由于EM算法可用于含有隐含变量的概率参数模型的最大似然估计。以wn为例,采用EM算法估计wn分布参数的公式如下
(5)
(6)
(7)
式中:r为迭代次数。使用EM算法对2个子高斯模型做参数估计的步骤如下[3]:首先采用K均值聚类算法获得p(wn)、μn、δn的初始值;然后利用式(5)~式(7)迭代更新p(wn)、μn、δn的值,直到相邻两次的p(wn)、μn、δn差值小于阈值ε(ε<10-8),则停止迭代,将最后一次迭代获得的参数作为最终结果。wc的分布参数求解方式相同。
利用EM算法估计wc和wn的统计分布参数后,根据贝叶斯最小误差率理论[13],计算满足式(8)时的最佳变化阈值T*如下
(8)
根据wc和wn的分布特性,结合式(3),将μn、δn、μc、δc代入式(8)中,则可得到T*的求解式
(9)
2.3 独立阈值法
通过自适应样本选择法得到了具有大比例变化量的训练样本,本文提出独立阈值法,利用选择得到的训练样本确定整幅影像的变化阈值。
综合上述分析,本文的变化检测方法流程图如图1所示。
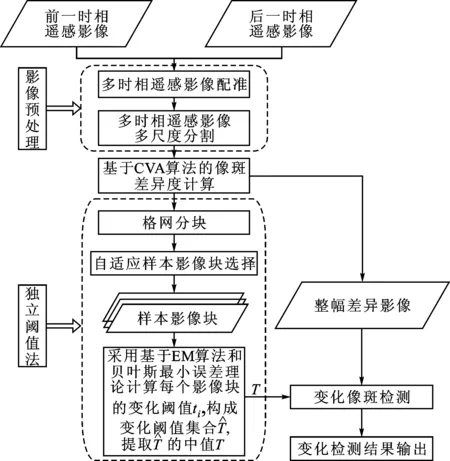
图1 本文的变化检测方法流程图
3 实验和分析
3.1 实验数据
实验数据是武汉市东湖地区2012年11月Worldview遥感影像和2013年8月的Pleiades遥感影像,影像的空间分辨率为0.5 m,由红、绿、蓝、近红外4个波段组成,影像均经过配准处理。实验数据1为城郊某区域,尺寸为7 103×7 887像素,如图2所示;实验数据2为城区某区域,尺寸为6 026×6 034像素,如图3所示。

(a)2012年影像 (b)2013年影像图2 实验数据1

(a)2012年影像 (b)2013年影像图3 实验数据2
3.2 实验分析
采用分形网络演化算法对配准后的实验数据进行多尺度分割,通过使用者的经验知识利用启发式的方法确定形状因子为0.5,紧致度为0.65,分割尺度参数为300。
分别对实验数据1和实验数据2按尺寸1 024×1 024像素进行格网分块,得到56个和36个影像块。采用样本选择法得到2个实验数据的样本影像块集合,其中2组实验数据的σi排序如图4所示,可见实验数据1和实验数据2在L=6和L=5处曲线的斜率变化明显,因此可利用前L个影像块构建样本影像块集合。
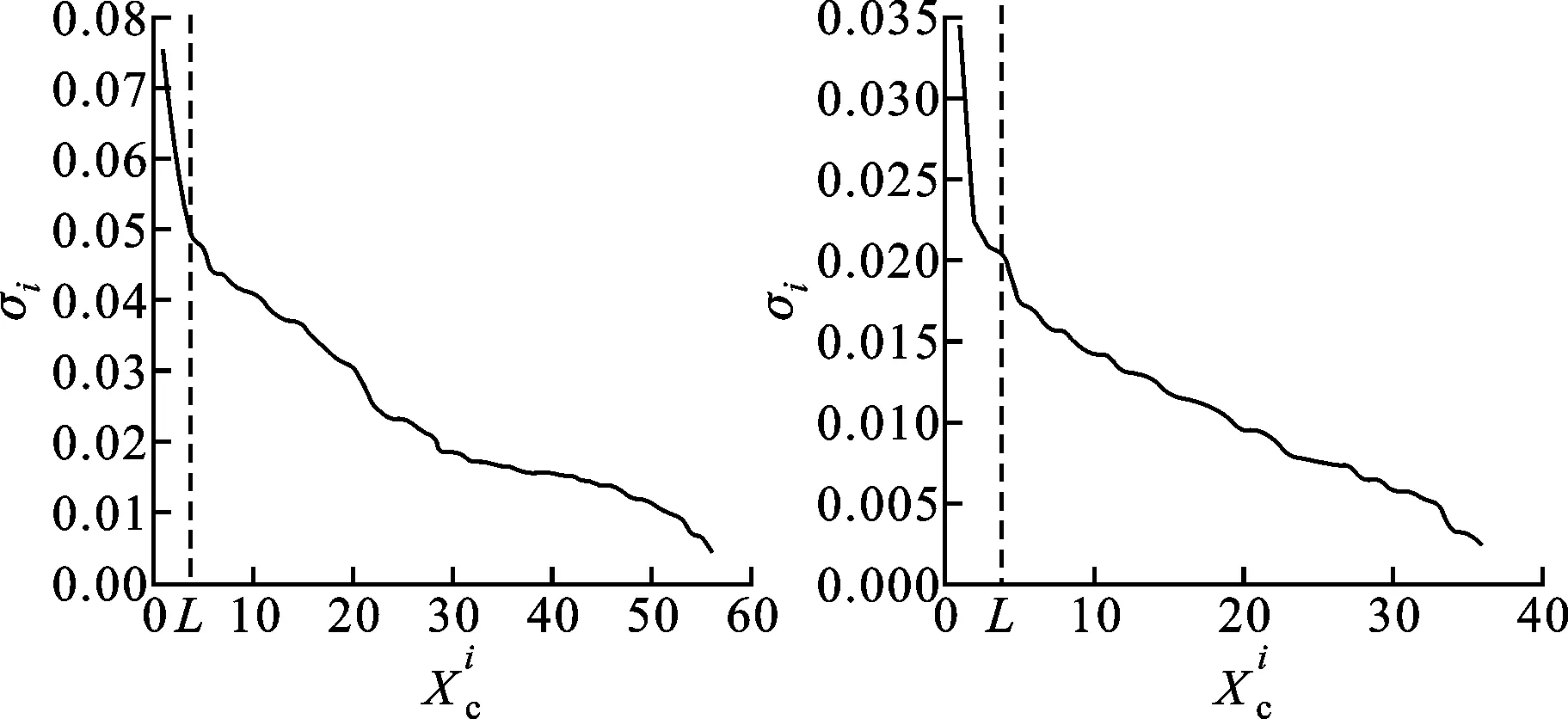
(a)实验数据1 (b)实验数据2图4 影像块标准差排序曲线
从2组实验数据的整幅实验结果中截取部分影像块的实验结果用于定量和定性分析本文方法的性能。从实验数据1中截取样本影像块A和非样本影像块B,见图2;从实验数据2中截取样本影像块C和非样本影像块D,见图3。
为了验证选择变化量比例较大的前L个差异影像块作为样本影像块的合理性,通过逐级增加L值,针对不同L值采用独立阈值法进行变化检测,利用实验数据1进行实验分析。L与变化检测精度的关系如图5所示:随着L的增大,正确率和虚检率的趋势平稳,漏检率逐步升高。可见本文选择的L值为6和5,较其他L值更为合理。
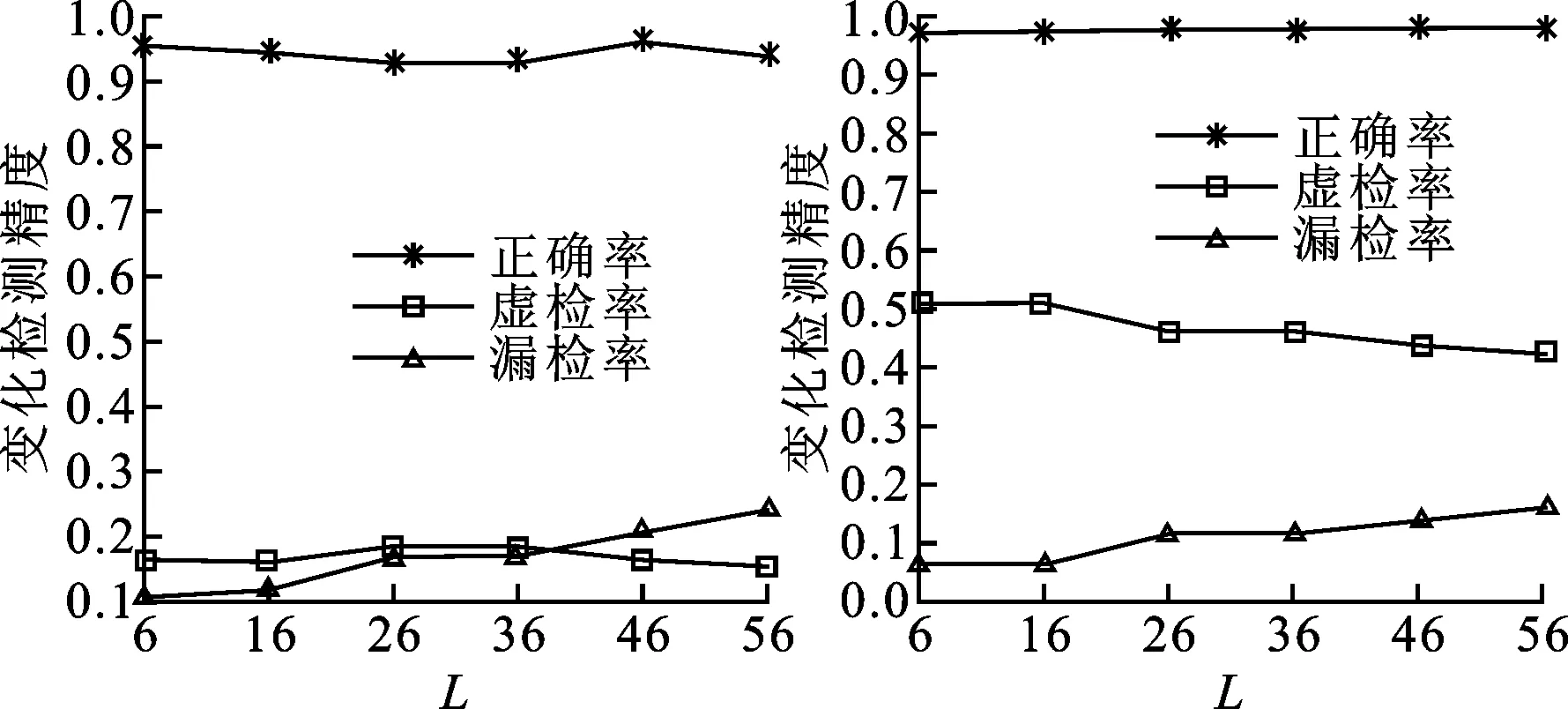
(a)影像块A (b)影像块B图5 L与变化检测精度的关系
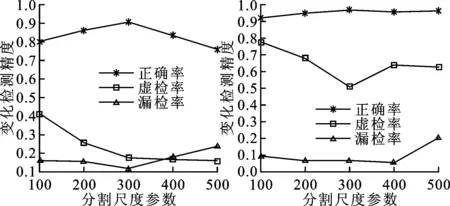
(a)影像块A (b)影像块B图6 分割尺度与变化检测精度的关系
分割尺度参数会影响采用面向对象方法的变化检测的精度。将实验数据1的分割尺度参数分别设置为100、200、300、400、500,在不同的分割尺度参数下采用独立阈值法进行变化检测,得到分割尺度参数与变化检测精度的关系如图6所示。从图6可知,分割尺度参数过小会导致较高的虚检率,分割尺度参数过大会导致漏检率升高,本文选择的分割尺度参数为300时可以得到最优的变化检测精度。
对独立阈值法中获得的样本影像块变化阈值集合取平均数,并将平均数作为整幅影像的变化阈值,记为均值阈值法。采用独立阈值法、均值阈值法、全局阈值法、局部阈值法分别对2组实验数据进行实验,利用人工方法获得的变化检测结果作为参考结果,验证本文方法的有效性。
针对实验数据1,独立阈值法得到的6个样本影像块变化阈值如表1所示。通过对表1中的变化阈值集合取中位数和平均数,获得独立阈值法和均值阈值法的变化阈值。4种方法的变化阈值如表2所示,可见独立阈值法与均值阈值法的变化阈值相同,低于全局阈值法,局部阈值法在影像块A与影像
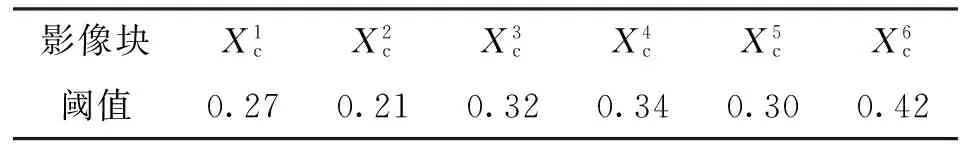
表1 实验数据1样本影像块的变化阈值

表2 实验数据1的4种方法的变化阈值
块B中得到不同的变化阈值。
影像块A和影像块B如图7a和7b、图8a和8b所示,4种方法的结果依次如图7c~7f和图8c~8f所示,变化检测精度如表3所示。通过图7和图8定性分析可知,独立阈值法和均值阈值法的变化检测效果相同,并优于其他两种方法,全局阈值法的漏检像斑多于独立阈值法,局部阈值法在影像块B中漏检较多。根据表3定量分析,独立阈值法与均值阈值法的变化检测精度相同,其正确率与其他两种方法差异不明显,虚检率略高于其他两种方法,但得到了最低的漏检率。
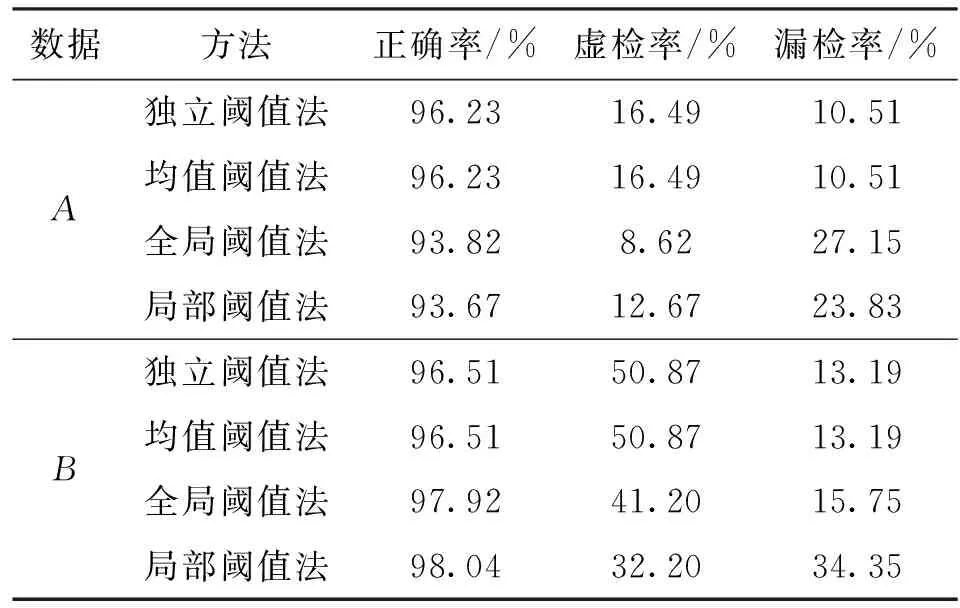
表3 实验数据1的4种方法变化检测精度

(a)2012年 (b)2013年 (c)独立阈值法(d)均值阈值法 (e)全局阈值法 (f)局部阈值法 (g)人工方法图7 影像块A的变化检测结果

(a)2012年 (b)2013年 (c)独立阈值法 (d)均值阈值法 (e)全局阈值法 (f)局部阈值法 (g)人工方法图8 影像块B的变化检测结果
针对实验数据2,独立阈值法得到的5个样本影像块变化阈值如表4所示。采用与实验数据1相同的方法获得独立阈值法和均值阈值法的变化阈值。

4种变化检测方法的变化阈值如表5所示, 独 表4 实验数据2的样本影像块变化阈值
立阈值法的变化阈值略低于均值阈值法,全局阈值法的变化阈值明显低于独立阈值法,局部阈值法中影像块C和影像块D的变化阈值差异明显。

表5 实验数据2的4种方法的变化阈值
影像块C和影像块D如图9a和9b、图10a和10b所示,4种变化检测方法的结果依次如图9c~9f和图10c~10f所示,变化检测精度如表6所示。通过图9、图10定性分析可知,独立阈值法获得最优的变化检测效果,均值阈值法的变化检测效果与独立阈值法相近,全局阈值法虚检严重,局部阈值法无法得到稳定的变化检测结果。通过表6定量分析,独立阈值法的正确率显著优于其他方法,在影像块C中虚检率分别高于均值阈值法和局部阈值法2.14%和4.42%,但漏检率分别降低了21.47%和58.65%,可见独立阈值法在牺牲少量虚检率的条件下有效降低了漏检率。
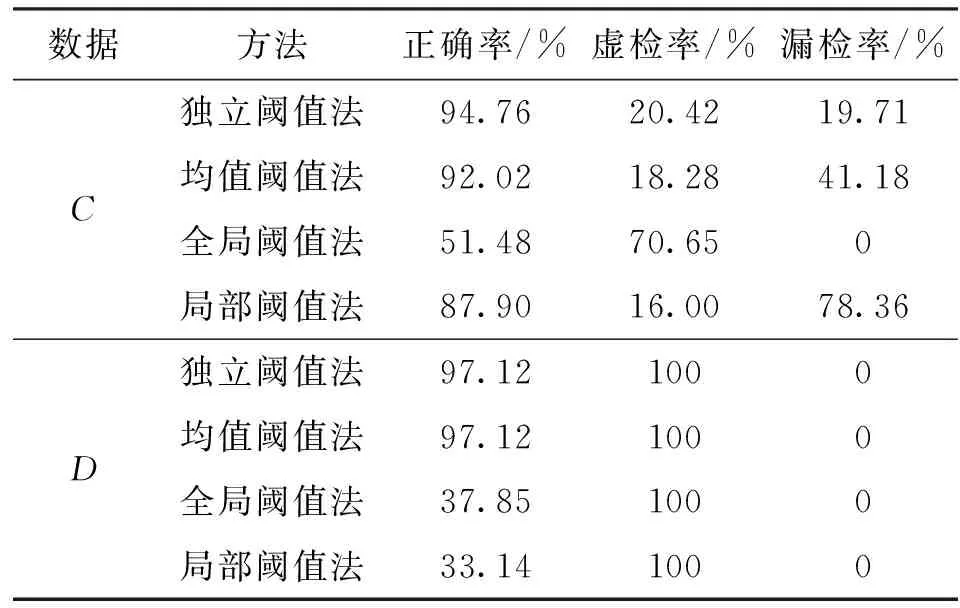
表6 实验数据2的4种方法变化检测精度

(a)2012年 (b)2013年 (c)独立阈值法 (d)均值阈值法 (e)全局阈值法 (f)局部阈值法 (g)人工方法图9 影像块C的变化检测结果

(a)2012年 (b)2013年 (c)独立阈值法 (d)均值阈值法 (e)全局阈值法 (f)局部阈值法 (g)人工方法图10 影像块D的变化检测结果
综上可知,全局阈值法和局部阈值法均无法获得准确的变化阈值,导致这两种方法的变化检测失败,该现象在城区的变化检测中尤为明显,平均正确率仅为44.67%和60.52%。均值阈值法尽管能够得到与独立阈值法相近的变检测结果,但易受极端数据的影响,如表4中样本影像块的变化阈值0.02,选择变化阈值集合的中位数作为整幅影像的变化阈值更稳定。独立阈值法能够获得准确的变化阈值,在城郊和城区的变化检测中均取得了优于均值阈值法、全局阈值法、局部阈值法的变化检测效果。
4 结束语
本文提出了采用独立阈值的遥感影像变化检测方法。该方法在样本选择的基础上采用独立阈值法确定差异影像的变化阈值并获取变化检测结果。实验结果表明,本文方法在对小比例变化量区域的多时相遥感影像变化检测中,能够取得优于常规的全局阈值法或局部阈值法的变化检测效果,适用于小比例变化量区域的多时相遥感影像变化检测。本文方法具有效率高、精度好等特点,能够满足城郊和城区等多种土地覆盖类型的变化检测,可为地理国情动态监测提供技术支持,在地理国情监测中具有一定应用价值。
[1] 李德仁, 眭海刚, 单杰. 论地理国情监测的技术支撑 [J]. 武汉大学学报: 信息科学版, 2012, 37(5): 506-512. LI Deren, SUI Haigang, SHAN Jie. Discussion on technologies of geographic national condition monitoring [J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 506-512.
[2] BRUZZONE L, PRIETO D F. Automatic analysis of the difference image for unsupervised change detection [J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(3): 1171-1182.
[3] 佃袁勇, 方圣辉, 姚崇怀. 一种面向地理对象的遥感影像变化检测方法 [J]. 武汉大学学报: 信息科学版, 2014, 39(8): 906-912. DIAN Yuanyong, FANG Shenghui, YAO Chonghuai. The geographic object-based method for change detection with remote sensing imagery [J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 906-912.
[4] 李亮, 龚龑, 李雪, 等. 像斑直方图相似性测度的高分辨率遥感影像变化检测 [J]. 遥感学报, 2014, 18(1): 139-153. LI Liang, GONG Yan, LI Xue, et al. Change detection based on similarity measurement of object histogram using high-resolution remote sensing imagery [J]. Journal of Remote Sensing, 2014, 18(1): 139-153.
[5] FARID M, GABRIELE M, SEBASTIANO B S. Unsupervised change-detection methods for remote-sensing images [J]. Optical Engineering, 2002, 41(12): 3288-3297.
[6] BAZY Y, BRUZZONE L, MELGANI F. Image thresholding based on the EM algorithm and the generalized Gaussian distribution [J]. Pattern Recognition, 2007, 40(2): 619-634.
[7] ROSIN P L. Thresholding for change detection [J]. Computer Vision and Image Understanding, 2002, 86(2): 79-95.
[8] DONNA H, LEEN K S, COSTAS T. A Dynamic thresholding technique for ice classification [C]∥Proceedings of International Geoscience and Remote Sensing Symposium. Los Alamitos, CA, USA: IEEE Computer Society, 1993: 638-640.
[9] CHEN Gang, HAY G J, CARVALHO L M T, et al. Object based change detection [J]. International Journal of Remote Sensing, 2012, 33(14): 4434-4457.
[10]ZHANG Qian, CAO Zhiguo, HU Zhongwen, et al. Joint image registration and fusion for panchromatic and multispectral images [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(3): 467-471.
[11]BENZ U C, HOFMANN P, WILLHAUCK G, et al. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS: ready information [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 58(3/4): 239-258.
[12]TANG Yuqi, ZHANG Liangpei, HUANG Xin. Object-oriented change detection based on the Kolmogorov-Smirnov test using high-resolution multispectral imagery [J]. International Journal of Remote Sensing, 2011, 32(20): 5719-5740.
[13]杨艺, 韩崇昭, 韩德强, 等. 一种多源遥感影像融合的新策略 [J]. 西安交通大学学报, 2010, 44(6): 88-92. YANG Yi, HAN Chongzhao, HAN Deqiang, et al. A novel fusion strategy for segmentation of multisensor remote sensing images [J]. Journal of Xi’an Jiaotong University, 2010, 44(6): 88-92.
[14]XUE Jinghao, TITTERINGTON D M. Median-based image thresholding [J]. Image and Vision Computing, 2011, 29(9) 631-637.
(编辑 刘杨)
A Change Detection Method of Remote Sensing Images with Independent Threshold
JIA Yonghong1,2,XIE Zhiwei1,ZHANG Qian3,YANG Gang4
(1. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;2. State Key laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University,Wuhan 430079, China; 3. School of Automation, Huazhong University of Science and Technology, Wuhan 430074,China; 4. School of Resource and Environmental Sciences, Wuhan University, Wuhan 430079, China)
A change detection method of remote sensing images based on an independent threshold is proposed to solve the problems that the accurate change threshold could not be worked out by either the general global or the local threshold methods, and the failure of change detection happens in multi-temporal remote sensing images change detection if the prior probability of the class of changed pixels in the detection region is low. The multi-scale image segmentation is used to get image objects from the multi-temporal remote sensing images, and differences of image objects are calculated from each image object based on the change vector analysis. Then, training samples that meet the expectation maximization algorithm and Bayesian rule with minimum error rate are correctly selected from the difference of image objects using the adaptive sample selection method. The change threshold is finally obtained from the training samples by the independent threshold method, and the change detection result is derived. Experimental results show that the proposed method gains more accurate change threshold. Comparisons with the global threshold method and the local threshold method show that the independent threshold method reduces the average miss rate by 9.6% and 17.24%, respectively, in the suburbs change detection, and improves the accuracy rate by 51.27% and 35.42%, respectively, in the urban change detection.
change detection; little change region; image object; sample selection; expectation maximization algorithm
2015-03-20。
贾永红(1966—),男,教授,博士生导师。
国家科技支撑计划资助项目(2011BAB01B05)。
时间:2015-10-03
10.7652/xjtuxb201512003
TP751
A
0253-987X(2015)12-0012-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151003.1919.008.html

