Adaptive Energy Detector and Its Application for Mismatched Signal Detection

Liu Wei-jianWang Li-caiDi Yuan-shuiJian TaoXie DangWang Yong-liang*

①(Air Force Early Warning Academy,Wuhan430019,China)

②(Unit93856of PLA,Lanzhou730060,China)

Adaptive Energy Detector and Its Application for Mismatched Signal Detection

Liu Wei-jian①Wang Li-cai①Di Yuan-shui②Jian Tao①Xie Dang①Wang Yong-liang*①

①(Air Force Early Warning Academy,Wuhan430019,China)

②(Unit93856of PLA,Lanzhou730060,China)

We investigate several important properties of an Adaptive Energy Detector (AED), which is originally proposed according to the Generalized Likelihood Ratio Test (GLRT), under the assumption that the signal steering vector is completely unknown. We show that the AED coincides with the Rao and Wald tests. We also give the exact statistical distribution, according to which one can easily derive the Probabilities of Detection (PD) and False Alarm (PFA), and we use the AED to design a parametrically tunable signal-mismatch detector. Compared to existing tunable detectors, the novel tunable detector is more flexible in governing the rejection of the mismatched signal; moreover, for the matched signal, the tunable detector can provide a higher PD than existing detectors. Two scalars, called the tunable parameters, control this functionality.

Adaptive Energy Detector (AED); Generalized Likelihood Ratio Test (GLRT); Rao test; Signalmismatch; Tunable detector; Wald test

1 Introduction

A common problem in signal processing is detecting a point or distributed target in a background of colored noise with unknown statistical properties[1-4]. This has been a topic of ongoing interest more than three decades. According to different design criteria, a large number of approaches are proposed under various scenarios. The most famous detectors for point-like target detection include Kelly's Generalized Likelihood Ratio Test (KGLRT)[5], Adaptive Matched Filter (AMF)[6], De Maio' Rao (DMRao) test[7], Adaptive Coherence Estimator (ACE)[8], Adaptive Beamformer Orthogonal Rejection Test (ABORT)[9], Whitened-ABORT (W-ABORT)[10], Double-Normalized AMF (DN-AMF)[11,12], and so on. For these detectors, it usually assumes that exact or rough knowledge about the signal steering vector is known a priori. However, in some practical applications, the aforementioned knowledge of the signal may not be available. Fewer papers consider the problem of adaptive detection with no information about the signal steering vector. In particular, in Ref. [13]under the assumption of completely unknown signature of the signal, the GLRT for a point target is proposed, which, for convenience, is denoted as the Adaptive Energy Detector (AED) in this paper. Moreover, the problem of detection of a distributed target with unknown signal steering vector is exploited in Ref. [14], and several GLRT-based detectors are proposed therein. The corresponding Rao and Wald tests are both developed in Ref. [15].

Another kind of problem usually encountered in practice is detection of a target in the presence of signal mismatch. That is to say, the actual signal steering vector is not aligned with the presumed one. This phenomenon occurs due to imperfect array calibration, spatial multipath, pointing errors, and so on. In order to design selective (less tolerant to signal mismatch) detectors, the ABORT and W-ABORT are proposed in Ref. [9]and Ref. [10], respectively. Therein, the hypothesis test is modified by adding a deterministic fictitious signal under the null hypothesis. This fictitious signal is assumed to be orthogonal to the nominal signal in the quasi-whitened[9]or truly whitened space[10]. Another method to devise selective detectors is adding a noise-like fictitious interference both under the null and alternative hypotheses[11,12,16]. The corresponding GLRT is found to have the same form as the ACE[16], while the Rao test and Wald test coincide with each other, referred to as the DN-AMF[11]. The ACE, ABORT, W-ABORT, and DN-AMF all have enhanced mismatched signal discrimination capabilities. However, they suffer certain performance loss for perfectly matched signals. In order to overcome this problem, the two-stage detectors[17-19]and tunable detectors[20-22]are proposed in the literature. The two-stage detectors[17-19]are formed by cascading two detectors with different abilities in terms of mismatched signals rejection. One declares the presence of a target only when data survive both detection thresholds.

However, the abilities of robustness to and rejection of a mismatched signal of the two-stage detectors are limited by these capabilities of their individual cascading detectors. In contrast, the tunable detectors[20-23]are of considerable flexibility in controlling the degree to which the mismatched signal is rejected through tuning one or more tunable parameters. However, the tunable detector in Ref. [20]has limited abilities of mismatched signal rejection, while the tunable detectors in Refs. [21-23]have limited robustness.

In this paper, we move a further step toward the design of adaptive detectors. The main contributions lie in the following two aspects. One is that we reconsider the problem of detecting a target of completely unknown signal steering vector. We derive the Rao and Wald tests, which are found to coincide with the GLRT in Ref. [13],i.e., the AED. Moreover, we give the exact statistical distribution of the AED. As a consequence, the Probabilities of Detection (PD) and False Alarm (PFA) are calculated easily. Another contribution is that by inspection of the similarity of the AED with several existing adaptive detectors, we propose a two-parameter tunable detector in anad hoc manner. The novel tunable detector possesses three distinct features. First, it is very general and covers the KGLRT, AMF, ABORT, WABORT, and AED as its five special cases. Second, the detection performance of the novel detector for matched signals is superior to that of existing detectors in some situations. Third, the novel tunable detector has more flexible ability of controlling the degree to which the mismatched signal is rejected. This function of the novel tunable detector is controlled by two tunable parameters.

The rest of the paper is organized in the following manner. Section 2 gives the problem formulation, while Section 3 shows that the Rao and Wald tests are equivalent to the AED, and gives its exact statistical distribution as well as its PD and PFA. Section 4 exploits the novel tunable detector. Numerical examples are given in Section 5. Finally, Section 6 concludes the paper.

2 Problem Formulation

For simplicity the radar antenna is assumed to be uniformly-spaced linear array antenna, consisting ofNelements. We want to discriminate between hypothesis H0that the data in the cell under test (primary data), sayx, contains only disturbance and hypothesis H1thatxcontains disturbancenand useful signalst=as.ais the unknown signal amplitude andsis the presumed signal steering vector. The disturbancen, including clutter and noise, is Gaussian distributed, with a mean zero and a covariance matrixR.Ris positive definitive Hermitian but unknown. To estimateR, it is customary to assume that a set of training data (secondary data),xl,l=1,2,...,L, is available. The secondary data are Independent and Identically Distributed (IID), contain no useful signal but for the noisenl.nlshares the same statistical properties as the noisenin the primary data. To sum up, the detection problem can be formulated as the following binary hypothesis test:

For convenience, letS=XXH, which isLtimes the sample covariance matrix (SCM), withX=[x1,x2,...,xL].

3 Rao and Wald Tests in the Case of Completely Unknown Signal Steering Vector

In this section, we first derive the Rao and Wald tests when the signal steering vectorsis unknown. These two detectors are both found to be identical to the AED, which is proposed according to the GLRT criterion and is given by[13]

Then we give the exact statistical distribution of the AED, according to which we derive the PD and PFA.

3.1 Rao test

The Fisher Information Matrix (FIM) for the parameter vector is[24]

where the superscript (.)*denotes the conjugate. Eq. (4) can be partitioned as

To derive the Rao test we need the joint Probability Density Function (PDF) ofxandXunder hypothesis H0, which is given by

where the symbols (.)H, tr(.), andstand for the conjugate transpose, trace, and determinantof a square matrix. Taking the derivative of the logarithm of Eq. (7) with respect to (w.r.t.)st, yields

Moreover, taking the derivative of Eq. (8) w.r.t.produces

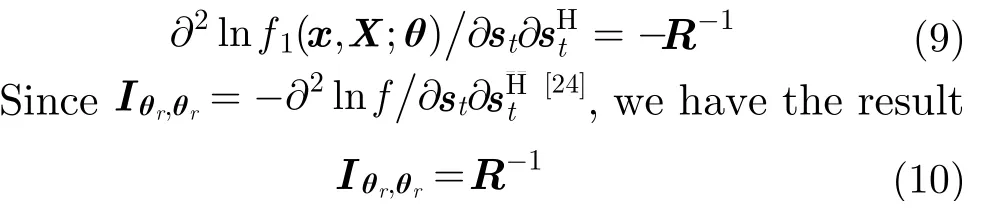
Substituting of Eq. (8) and Eq. (10) into Eq. (6), along with the fact thatstunder hypothesis H0reduces to the null vector, results in the Rao test for givenR

It is easy to show that the MLE ofRunder hypothesis H0isInserting it into Eq. (11), and dropping the constant scalar, after some algebra, yields the final Rao test

which is statistically equivalent to

which in turn is the exact the AED in Eq. (2).

3.2 Wald test

The Wald test is given by[24]

Clearly, the MLE ofRunder hypothesis H1isPlugginginto Eq. (16), and dropping the constant scalar, leads to the final Wald test

which is exactly the AED in Ref. [13].

Note that the derivations of the Rao test and Wald test above are parallel to those in Ref. [15]. Actually, the Rao and Wald tests in this paper are special cases of the corresponding Rao and Wald tests in Ref. [15]. Specifically, the Rao test in Eq. (12) is the Rao test in Eq. (11) in Ref. [15]whenM=1 therein, while the Wald test in Eq. (17) is the Wald test in Eq. (17) in Ref. [15]for the case ofM=1. However, we would like to present the detailed derivations above, since utilization of the Rao or Wald test to design a detector is not as common as the GLRT criterion. Moreover, it is also noteworthy that the two-step GLRT, two-step Rao test, and two-step Wald test are all identical to Eq. (13). For the sake of brevity, the derivations are not given here. Finally, it is also worthy to point out that the AED is Uniformly Most Powerful Invariant (UMPI)[25].

3.3 Exact statistical distribution of AED

Eq. (13) can be recast as

andNandL-N+1 DOFs, denoted as

whereris defined as the Signal-to-Clutter-plus-Noise Ratio (SCNR).

Hence, according to the Cumulative Distribution Function (CDF) of the noncentral complex F-distribution[27], we can obtain the PD of theAED, described as

where IGk+1(a) is the incomplete Gamma function, with the expression

Note that Eq. (21) is equal to the PD of the AED derived in Ref. [13]. Precisely, replacingkandbyi-1 andy0-1, respectively, in Eq. (21) does not change the result but leads to a form identical to the PD of the AED in Eq. (10) in Ref. [13].

Remarkably, the PFA in Eq. (22) is more convenient than the PFA given in Eq. (3) in Ref. [13]to numerically calculate the detection threshold, since Eq. (22) only contains finite-sum term, whereas Eq. (3) in Ref. [13]is involved in a hypergeometric function.

Eq. (21) and Eq. (22) are for the case of the deterministic target. For completeness, we also consider the case of the fluctuation target. Precisely, we consider the Swerling I target model. Since the PFA, given in Eq. (22), does not contain the target property. It is the same for the random and deterministic target. Hence, we only need to calculate the PD for the fluctuation target. In this case, the amplitude of the signal is modeled as a complex Gaussian random variable[13]. Accordingly, the SCNRrhas an exponential density function[13]given by

where IGk+1(a) is the incomplete Gamma function, as mentioned above.

Averaging Eq. (21) over Eq. (23) and using Eq. (24), we have the PD of the AED for the Swerling I target

For comparison purpose, we briefly derive the PDs of the KGLRT, AMF, DMRao, and ACE for the Swerling I target in the following. The analytical expressions for the PDs of the KGLRT, AMF, ACE, and DMRao are well-known (see,e.g., Refs. [7,17]). For simplicity, they are not repeated here. Averaging these expressions over Eq. (23), along with Eq. (24), we have the corresponding conditional PDs

Note that Eq. (25)-Eq. (29) hold both for matched and mismatched signals. The signal mismatch occurs when the nominal steering vector, such as the array steering,sis not aligned withthe actual signal steering vectors0. To quantify the amount of the signal mismatch, we resort to the cosine squared of the anglefbetweensands0in the whitened space. That is to say, we have

When the signal is deterministic, the PDF ofbunder hypothesis H1is given by (A2-23) in Ref. [27],i.e.,

which is the PDF of the quantitybin Eq. (30) under hypothesis H1for the Swerling I target. Finally, averaging Eq. (25)-Eq. (29) over Eq. (33) results in the final PDs for the Swerling I target.

4 Novel Tunable Detector for the Case of Signal Mismatch

The AED does not assume any information about the signal steering vector. Furthermore, it does not contain the actual signal steering. Hence, the AED is not affected by the signal mismatch. According to this characteristic of the AED, as well as the relationship between the AED and other detectors, we introduce a two-parameter tunable detector when signal mismatch exists in this section.

The AMF for the problem of Eq. (1) is found to be[6]

Moreover, the ABORT[9]and W-ABORT[10]are found to be

respectively.

By comparing the aforementioned detectors with the AED in Eq. (13), we introduce the following novel tunable detector

which is referred to as the MEAWK. The letters in the acronym MEAWK stand for the AMF, AED, ABORT, W-ABORT, and KGLRT, respectively.

Notice that whena=g=0, Eq. (39) degenerates into the AMF; whena=0 andg=1, it reduces to the ABORT; whena=1 andg=0, it is equal to the AED; whena=g=1, it is statistically equivalent to KGLRT; whena=1 andg=2, it becomes the W-ABORT.

A quick comment on the MEAWK is that it possesses the Constant False Alarm Rate (CFAR) property, because the AMF is CFAR, and the quantitiesbin Eq. (30) andxHS-1xare both essentially not related to the covariance matrixR[6,17]. Moreover, the MEAWK nearly has the same computational complexity with the AMF, AED, ABORT, W-ABORT, and KGLRT, since the main computational burden for them is the same, and it is the matrix inversion ofS.

In light of Eq. (35) and Eq. (30), we have the important stochastic representation of the MEAWK

The exact PD and PFA can be calculated according to the solution of the equationβ+α(1-β) (withβbeing the sole unknown) and the four cases: 1)However, since the above equation does not admit a close-form solution in general, the analytical PD and PFA are intractable except for some special cases. Hence, we resort to the Monte Carlo simulations to evaluate the detection performance of the MEAWK, both for matched and mismatched signals. For simplicity, only the deterministic signal is considered.

5 Numerical Examples

In this section, we first compare the detection performance of the AED with other relative detectors. Then we evaluate the detection performance of the MEAWK.

5.1 AED

In this subsection, we compare the detection performance of the AED with some well-known detectors, namely, the KGLRT, AMF, ACE, and DMRao. Precisely, we compare their PDs for the deterministic, random, matched, and mismatched signals. As for the random signal, only the Swerling I fluctuation model is considered.

The noise is modeled as an exponentially correlated random vector with one-lag correlation coefficient. That is to say, the (i,j)-th element of the covariance matrixRis given byσ2ε│i-j│,i,j=1,2,...,N, withσ2=1 andε=0.95. Moreover, to reduce the computational complexity, the PFA is set to PFA=10-3, and we chooseN=12 andL=2Nin all figures. For the Monte Carlo simulations, to evaluate the PD and the threshold necessary to ensure a prescribed PFA, we resort to 2×104and 200/PFA independent data realizations, respectively.

Fig. 1 shows the PD of the AED for matched signals, also in comparison with the KGLRT, AMF, ACE, and DMRao. The signal is assumed to be known up to an unknown scaling factor,i.e.,st=as0, where the actual signal steering vectors0is known a priori and the signal amplitudeais unknown. The subscripts “TH” and “MC” in the legend stand for theoretical results and Monte Carlo simulation result, respectively. It is seen that the theoretical results match the Monte Carlo simulation results pretty well. Moreover, when the signature of the signal is known a priori, the PD of the AED is lower than those of the other detectors. This seems reasonable, since the knowledge of the signature of the signal is not taken into account by the AED. Particularly, the KGLRT has the highest PD. Furthermore, compared with the case that the deterministic signal model, it needs additional SCNR to achieve the same PD for a certain detector for random signals.

Fig. 2 depicts the detection performance of the detectors for mismatched signals. In Fig. 2, the signal mismatch quantity cos2φ, defined in Eq. (31), is set to be 0.7. It is shown that under this system parameters, the AED exhibits the highest PD both for random and deterministic signal. Note that in Fig. 2(b) only the Monte Carlo results are provided.

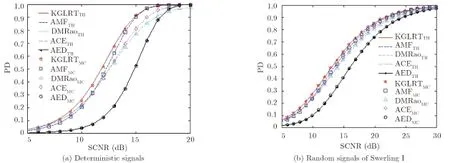
Fig. 1 PDs of the KGLRT, AMF, DMRao, ACE, and AED for matched signals

Fig. 2 PDs of the KGLRT, AMF, DMRao, ACE, and AED for mismatched signals

5.2 MEAWK

In this subsection, we compare the detection performance of the MEAWK with its natural competitors, both for matched and mismatched signals. The operational parameters are the same as those in the above subsection.

We use Eq. (40) rather than Eq. (39) to perform Monte Carlo simulations. A remarkable advantage of Eq. (40) is that it does not need any matrix multiplication or matrix inversion operation. Compared to Eq. (39), this reduces the computational complexity significantly.

Fig. 3 shows the PD of the MEAKW with different tunable parameters, also in comparison with the KGLRT (i.e., the plan shown in Fig. 3). For convenience, the values of the PD of the MEAWK less than 0.8 are set to be 0.8. It is shown that with many pairs of tunable parametersaandg, the MEAWK can provide a higher PD than the KGLRT.

Fig. 3 PDs of the MEAWK with different tunable parameters for matched signals. SCNR=16 dB

The detection performance of the MEAWK, with specificganda, under different SCNRs is displayed in Fig. 4. The results highlight that the MEAWK can provide a higher PD than the other detectors for all the values of the SCNR in the interval between 8 dB and 16 dB.

Fig. 4 PD versus SCNR for mismatched signals.a=0.6 andg=0.8

Fig. 5 demonstrates the detection performance of the detectors for mismatched signals. The amount of the signal mismatch is quantified by Eq. (31). The results in Fig. 5 indicate that the MEAWK, with appropriate tunable parameters, can be either more robust or more selective than the existing detectors, depending on the system requirement.

6 Conclusions

Fig. 5 PD versus cos2ffor mismatched signals. SCNR=20 dB

In the first part of the paper, we have considered the problem of detecting a target, with completely unknown signature. We derive the Rao and Wald tests, which coincide with the GLRT,i.e., the AED. Moreover, we derive the exact statistical distribution of the AED. According to this distribution, one can easily calculate the PD and PFA. Moreover, it is shown that the AED is more robust to the signal mismatch than other detectors. At the second part of the paper, we propose a two-parameter tunable detector,i.e., the MEAWK. This idea is inspired by the relationship between the AED and other detectors. The MEAWK is of considerable flexibility in governing the level to which the mismatched signal is rejected. With proper tunable parameters, it can exhibit improved detection performance w.r.t. its natural competitors for matched signals. In addition, it can also become more robust or more selective than the existing detectors for mismatched signals. As for how to select the tunable parameters, a rule of thumb is that if a selective detector is needed to reject mismatched signals, the values of the tunable parameters should be set relatively large[23]. An instance is that a radar workswin tracking mode. On the other hand, if a robust detector is needed, the values of the tunable parameters should be set as small as possible. An example is that a radar operates in searching mode.

[1]Liu J, Li H, and Himed B. Threshold setting for adaptive matched filter and adaptive coherence estimator[J].IEEE Signal Processing Letters, 2015, 22(1): 11-15.

[2]Shi B, Hao C, Hou C,et al.. Parametric Rao test for multichannel adaptive detection of range-spread target in partially homogeneous environments[J].Signal Processing, 2015, 108: 421-429.

[3]Cui G, Liu J, Li H,et al.. Signal detection with noisy reference for passive sensing[J].Signal Processing, DOI: 10.1016/j.sigpro.2014.09.034.

[4]Liu W, Xie W, Liu J,et al.. Adaptive double subspace signal detection in Gaussian background-part I: Homogeneous environments[J].IEEE Transactions on Signal Processing, 2014, 62(9): 2345-2357.

[5]Kelly E J. An adaptive detection algorithm[J].IEEE Transactions on Aerospace and Electronic Systems, 1986, 22(1): 115-127.

[6]Robey F C, Fuhrmann D R, Kelly E J,et al.. A CFAR adaptive matched filter detector[J].IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208-216.

[7]De Maio A. Rao test for adaptive detection in Gaussian interference with unknown covariance matrix[J].IEEE Transactions on Signal Processing, 2007, 55(7): 3577-3584.

[8]Kraut S and Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J].IEEE Transactions on Signal Processing, 1999, 47(9): 2538-2541.

[9]Pulsone N B and Rader C M. Adaptive beamformer orthogonal rejection test[J].IEEE Transactions on Signal Processing, 2001, 49(3): 521-529.

[10]Bandiera F, Besson O, and Ricci G. An ABORT-like detector with improved mismatched signals rejection capabilities[J].IEEE Transactions on Signal Processing, 2008, 56(1): 14-25.

[11]Orlando D and Ricci G. A Rao test with enhanced selectivity properties in homogeneous scenarios[J].IEEE Transactions on Signal Processing, 2010, 58(10): 5385-5390.

[12]Liu W, Xie W, and Wang Y. A Wald test with enhanced selectivity properties in homogeneous environments[J].EURASIP Journal on Advances in Signal Processing, 2013, 2013(14): 1-4.

[13]Raghavan R S, Qiu H F, and Mclaughlin D J. CFAR detection in clutter with unknown correlation properties[J].IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 647-657.

[14]Conte E, De Maio A, and Galdi C. CFAR detection of multidimensional signals: an invariant approach[J].IEEE Transactions on Signal Processing, 2003, 51(1): 142-151.

[15]Liu W, Xie W, and Wang Y. Rao and Wald tests for distributed targets detection with unknown signal steering[J].IEEE Signal Processing Letters, 2013, 20(11): 1086-1089.

[16]Besson O. Detection in the presence of surprise or undernulled interference[J].IEEE Signal Processing Letters, 2007, 14(5): 352-354.

[17]Richmond C D. Performance of the adaptive sidelobe blanker detection algorithm in homogeneous environments[J].IEEE Transactions on Signal Processing, 2000, 48(5): 1235-1247.

[18]Bandiera F, Besson O, Orlando D,et al.. An improved adaptive sidelobe blanker[J].IEEE Transactions on Signal Processing, 2008, 56(9): 4152-4161.

[19]Hao C, Liu B, and Cai L. Performance analysis of a twostage Rao detector[J].Signal Processing, 2011, 91(8):2141-2146.

[20]Kalson S Z. An adaptive array detector with mismatched signal rejection[J].IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 195-207.

[21]Hao C, Liu B, Yan S,et al.. Parametric adaptive radar detector with enhanced mismatched signals rejection capabilities[J].EURASIP Journal on Advances in Signal Processing, 2010, DOI: 1155/2010/375136.

[22]Bandiera F, Orlando D, and Ricci G. One- and two-stage tunable receivers[J].IEEE Transactions on Signal Processing, 2009, 57(8): 3264-3273.

[23]Liu W, Xie W, and Wang Y. Parametric detector in the situation of mismatched signals[J].IET Radar,Sonar&Navigation, 2014, 8(1): 48-53.

[24]Liu W, Wang Y, and Xie W. Fisher information matrix, Rao test, and Wald test for complex-valued signals and their applications[J].Signal Processing, 2014, 94: 1-5.

[25]Bose S and Steinhardt A O. Adaptive array detection of uncertain rank one waveforms[J].IEEE Transactions on Signal Processing, 1996, 44(11): 2801-2809.

[26]Muirhead R J. Aspects of Multivariate Statistical Theory[M]. 2nd ed. Hoboken: Wiley, 2005: 98.

[27]Kelly E J and Forsythe K M. Adaptive detection and parameter estimation for multidimensional signal models[R]. Lincoln Laboratory, Lexington, 1989.

Liu Wei-jian was born in Shandong Province, China, in 1982. He received the B.S. degree in information engineering and M.S. degree in signal and information processing both from Air Force Radar Academy, Wuhan, China, in 2006 and 2009, respectively, and the Ph.D. degree in information and communication engineering from National University of Defense Technology, Changsha, China, in 2014. He is a lecturer at Air Force Early Warning Academy. His current research interests include multichannel signal detection, statistical and array signal processing.

E-mail: liuvjian@163.com

Wang Li-cai was born in Shandong Province, China, in 1974. He received the B.S. degree in radar engineering from Air Force Radar Academy, Wuhan, China, in 2001. He is an engineer in radar engineering at Air Force Early Warning Academy, Wuhan, China. His current research interests include radar systems and signal processing.

E-mail: 1250319472@qq.com

Di Yuan-shui was born in Shandong Province, China, in 1965. He received the B.S. degree in radar engineering from Air Force Radar Academy, Wuhan, China, in 1989. He is a senior engineer at Unit 93856 PLA. His current research interests include radar systems and signal processing.

E-mail: 2495451301@qq.com

Jian Tao was born in Hubei Province, China, in 1982. He received the B.S. degree in computer science and technology from Wuhan Institute of Technology, Wuhan, China, in 2005 and the M.S. degree in signal and information processing from Air Force Radar Academy, Wuhan, China, in 2009. He is a lecturer at Air Force Early Warning Academy. His current research interests include data processing and adaptive filtering.

E-mail: jthffzwl@163.com

Xie Dang was born in Anhui Province, China, in 1979. He received the B.S. degree in information and computing science from Hangzhou Dianzi University, China, in 2003 and the M.S. degree in signal and information processing from Air Force Radar Academy, Wuhan, China, in 2009. He is a lecturer at Air Force Early Warning Academy. His current research interests include spatial spectrum estimation and array signal processing.

E-mail: 9smile9@163.com

Wang Yong-liang was born in Zhejiang Province, China, in 1965. He received the B.S. degree in electrical engineering from Air Force Radar Academy, Wuhan, China, in 1987 and the M.S. and Ph.D. degrees in electrical engineering from Xidian University, Xi'an, China, in 1990 and 1994, respectively. From June 1994 to December 1996, he was a Post-doctoral Fellow with the Department of Electronic Engineering, Tsinghua University, Beijing, China. Since January 1997, he has been a Full Professor and the Director of the Key Research Laboratory, Air Force Early Warning Academy. His recent research interests include radar systems, space-time adaptive processing, and array signal processing. He has authored or coauthored three books and more than 200 papers. Dr. Wang is the recipient of the China Postdoctoral Award of 2001 and the Outstanding Young Teachers Award of the Ministry of Education, China of 2001.

E-mail: ylwangkjld@163.com

刘维建, 王利才, 狄源水, 等. 自适应能量检测器及在失配信号检测中的应用[J]. 雷达学报, 2015, 4(2): 149-159. http://dx.doi.org/10.12000/JR14132.

自适应能量检测器及在失配信号检测中的应用
刘维建①王利才①狄源水②简 涛①谢 谠①王永良①

①(空军预警学院 武汉 430019)

②(93856部队 兰州 730060)

自适应能量检测器(AED)是一种信号导向矢量完全未知时有效的检测器，最早根据广义似然比(GLRT)准则得到。该文首先分析了AED一些重要特性。指出AED与根据Rao准则和Wald准则得到的检测器相同，并得到了其精确的统计分布，根据该统计分布进而较容易地推导出AED解析的检测概率(PD)和虚警概率(PFA)。其次利用AED设计了一种信号失配情形下的参数可调检测器。与现有的参数可调检测器相比，新检测器对失配信号的检测具有更好的灵活度。此外，对于匹配信号，新检测器具有更高的检测概率。该可调检测器的这些功能通过调节两个标量参数实现，两个参数被称为可调参数。

自适应能量检测器(AED)；广义似然比；Rao检测器(GLRT)；信号失配；可调检测器；Wald检测器

TN911.23

A

2095-283X(2015)02-0149-11

10.12000/JR14132

Manuscript received November 17, 2014; revised January 28, 2015. Published online April 28, 2015.

Supported in part by National Natural Science Foundation of China (61102169).

*Communication author: Wang Yong-liang.

E-mail: ylwangkjld@163.com.

CLC index:TN911.23

Reference format:Liu Wei-jian, Wang Li-cai, Di Yuan-shui,et al.. Adaptive energy detector and its application for mismatched signal detection[J].Journal of Radars, 2015, 4(2): 149-159. http://dx.doi.org/ 10.12000/JR14132.