基于异步电机的风力机模拟仿真实验研究

潘巧波

(东北电力大学 自动化工程学院，吉林 吉林 132012)

目前风力发电及其相关技术得到了迅猛的发展，变桨控制、恒频变流、直接驱动等许多关键技术从实验环境走向工业现场，并得到普遍的推广［1］。基于此，风力发电技术研究的最理想方法是将发电机与风力机直接连接，在工业现场做相关实验。但是这样的做法，研究经费昂贵，对实验的环境要求也较为苛刻。因此有必要在实验室环境下构造风力发电试验平台，从而解决在实验室里进行风力机发电技术研究的难题［2－3］。在以往国内外与风机模拟相关的文献中，绝大多数是采用直流电机来模拟风力机特性，但是由于直流电机自身固有的缺陷，不适于构建功率较大的风电发电试验平台。近几年来，随着交流异步电机控制技术的逐步成熟，基于异步电机的风机特性模拟成为新的研究方向。本文基于异步电机的矢量控制思想，通过对异步电机转矩与转速的控制，使其按照风力机的特性运行，以模拟真实风力机输出特性［4］。

1 风力机特性分析及模拟

理论计算证明，理想风轮机最大风能转化效率为59.3%，风轮所提取的能量等于气流进出口的动能差。风力机实际能获得的有用功率输出为

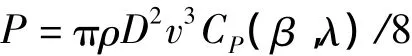
式中:ρ为空气密度;D为风力机叶片直径;v为风速;Cp为风能利用系数，即叶片桨距角和叶尖速比λ的相关函数，若保持风速不变，此时Cp值的大小由λ决定。λ为叶尖的圆周速度与风速之比，即

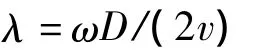
式中:ω 为风轮角速率，rad·s－1。

对于特定的风力机，Cp最大值时的叶尖速比称为最佳叶尖速比λopt，相应的Cp称之为最大风能利用系数，用Cpmax表示。当 λ偏离 λopt时，Cp都会小于唯一的Cp最大值，从而引起机组发电功率的降低。不同的桨距角β，Cp变化如图1所示。

由转矩与功率之间关系式T=P/ω得到风力机输出转矩为

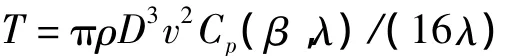
转矩与转速特征曲线如图2所示。

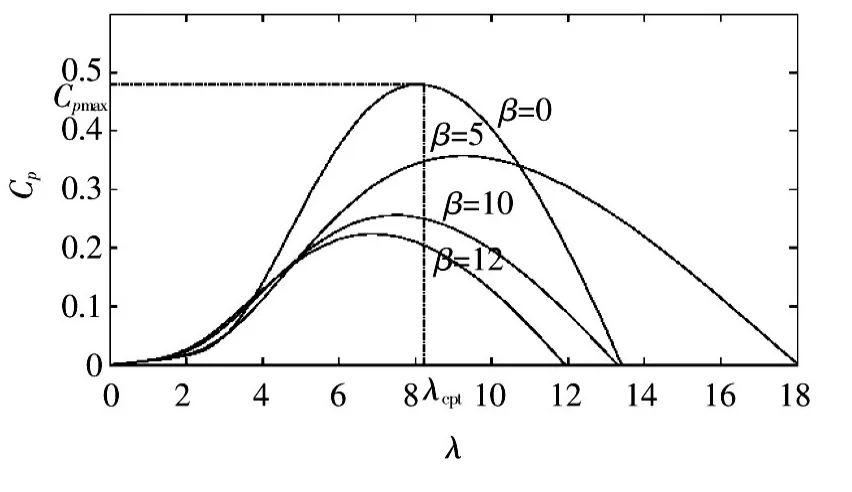
图1 β变化下风力机CP－λ曲线Fig.1 CP－λ curve of wind turbine in β change condition

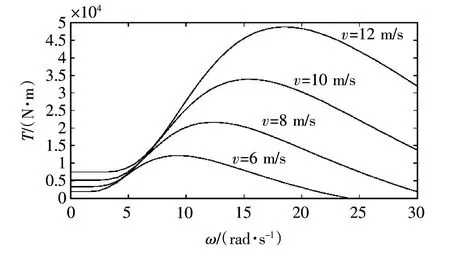
图2 风力机T－ω曲线Fig.2 T－ω change curve of wind turbine

把风力机回馈的转速值(模拟电机转速)，以及实际的风速值代入上述风力机特性公式可以得到风力机的输出转矩，并作为异步电动机模拟风力机的控制信号。计算转矩用的风力机模型如图3所示，其中风能利用系数的函数关系可从实际风机的经验公式得到。仿真结果表明，异步电机输出的转矩与实际风力机输出转矩的特性一致，达到了本次试验异步电机模拟风力机特性的预期目的。

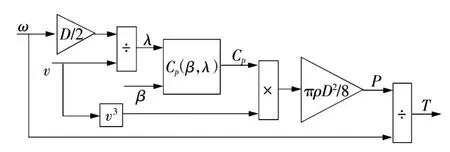
图3 风力机数学模型Fig.3 Wind turbine mathematical model

2 异步电机的工作原理及控制策略

2.1 矢量坐标变换的方法

矢量坐标变换分为三相静止坐标到两相静止坐标的变换(3s/2s)、两相静止坐标到两相旋转坐标的变换(2s/2r)和三相静止坐标到两相静止坐标的变换(3s/2r)。本文直接给出(3s/2r)变换的方法。

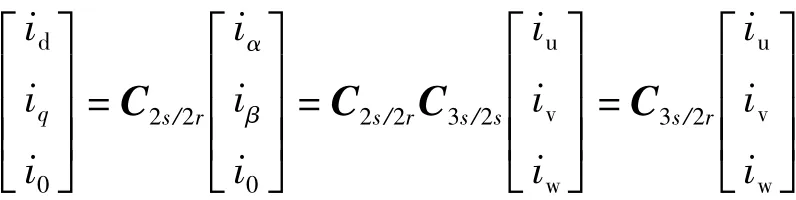
式中，三相静止坐标到两相旋转坐标的变换矩阵为

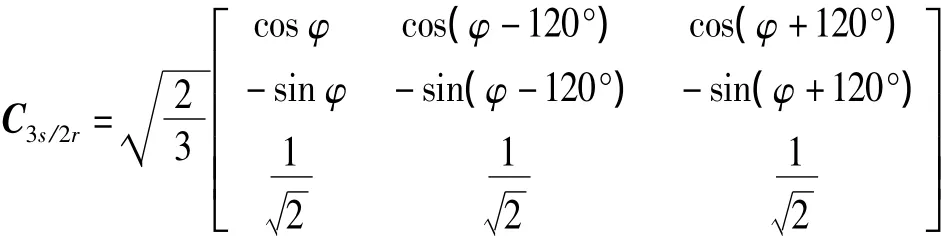
式中，φ为d－q坐标系d轴与α－β坐标系α轴之间的夹角。

如果旋转坐标系的旋转速度等于静止绕组产生的旋转磁动势的角速度，那么d－q坐标系可改为M－T坐标系，相应的变量也可由d、q改为M、T。

2.2 异步电机的矢量控制思想

交流异步电机是非线性、强耦合性的系统［5］，其输出转矩的控制相对于直流电机要更为复杂。所以根据磁动势和功率等效的原则，异步电动机需进行坐标变换将定子电流分解为同步旋转坐标下的励磁电流分量和转矩电流分量，然后对这两个分量加以单独控制。异步电机的坐标变换如图4所示。

图4 异步电机的坐标变换示意图Fig.4 of Coordinate transformation schematic diagram of asynchronous motor

在三相坐标系中，定子交流 iu、iv、iw，通过(3s/2s)变换为两相静止坐标系上的交流电流iα和iβ，再经过(3s/2s)变换为同步旋转坐标下的直流电流im和it。在坐同步旋转坐标下，可以把对异步电机的控制近视为他励直流电机。ism和ist分别相当于直流电机的励磁电流和电枢电流。异步电机等效成直流电机后，可按照控制直流电机的方法对异步电机进行控制。矢量控制原理如图5所示。

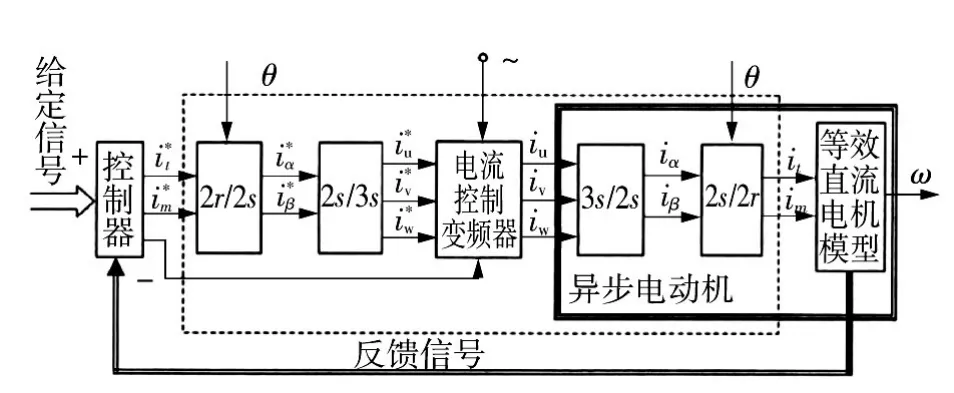
图5 电机矢量控制原理图Fig.5 Motor vector control principle diagram

2.3 异步电机矢量控制方案

在M－T坐标系下，按转子磁链定向推倒，可得异步电机的矢量控制方程为

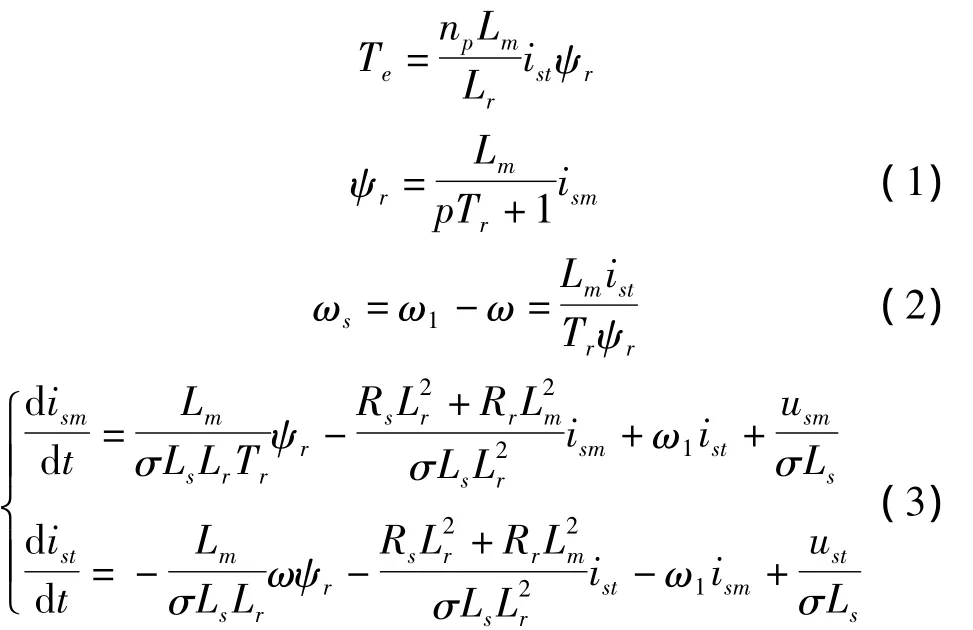
式中:σ为电机漏磁系数，σ=1－Lm/LsLr;Tr为转子电磁时间常数，Tr=Lr/Rr。

通过矢量控制方程(1)，可以计算得到电机转子磁链ψr。通过矢量控制方程(2)，可以计算得到电机转差ωs以及定子频率(ω1=ωr+ωs)。如果采取磁通不变的控制 ψrn=ψrd=ψr，ψrt=ψrq=0，由式(1)可得 ψr=LmLsm，代入式(2)可得 ωs=ist/Trism。

对异步电机的矢量控制，需要确定转子磁链的位置，而实际上对其直接测量很难实现。故本文采用基于转差频率的间接矢量控制，这种控制方式利用电机的转速和按照控制算法得到的转差频率之和来估计磁链相对于定子的位置［6］。其结构相比真实计算出转子磁链的相位与幅值来说相对简单，而且可得到较好的实验效果和动态特性，这种矢量控制的原理如图6所示。

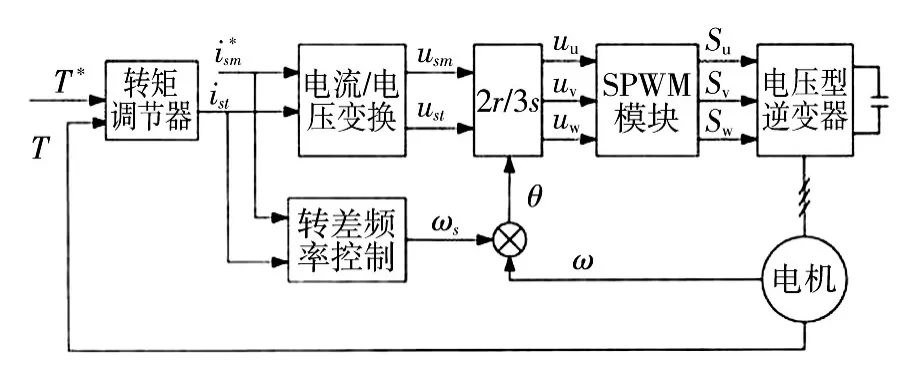
图6 转差型矢量控制原理图Fig.6 Slip type vector control principle diagram

由图6可知，按照以上算法确定定子电流的励磁分量ism为一恒值后，转矩分量ist可由风力机数学模型计算获得转矩给定信号与电机输出转矩回馈作差，再经转矩调节器ATR得到。另外由于本实验采用电压型逆变器，需要将矢量控制方程得到的定子电力转矩分量和励磁分量转换成相应的电压控制信号。对式(3)进行整理，可得定子电压和电流的转换公式为

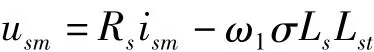
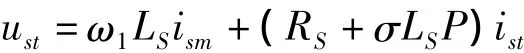
usm、ust经过两相旋转坐标到三相静止坐标变换(2r/3s)，得到SPWM逆变器的三相电压控制信号，并控制逆变器的输出电压，则逆变器便可以输出异步电机调速所需的三相变频电压及电流，从而达到控制电机转速和转矩的目的。

3 模拟仿真实验

根据对风力机特性的分析，转矩由风力机叶尖转速和实际风速决定。因此，异步电机模拟风力机特性的基本思路就是通过风力机模型根据当前环境的实际风速和回馈的风力机转速(实际为模拟电机转速)，理论计算出风力机输出转矩，然后异步电机的控制系统根据这个转矩信号控制电机的运行，使其输出特性与实际风力机一致，以此实现风力机特性的模拟。本文采用异步电动机在实验室中代替风力机拖动风力发电机，其结构如图7所示。

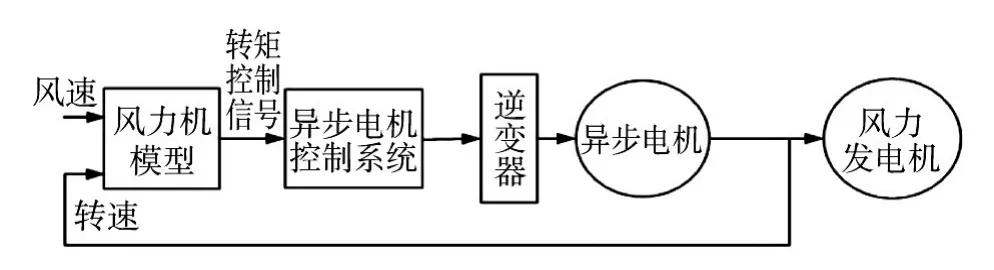
图7 风力机模拟系统原理图Fig.7 Wind turbine simulation system schematic diagram

以上模拟系统主要由3部分组成:风力机模型、异步电机的控制部分以及异步电机模型。其中，风力机模型由数学模块搭建;异步电机控制系统采用基于转差频率的间接矢量控制算法;电机采用理想的异步电机模型。

在Matlab/Simulink中搭建了风力机模拟试验平台如图8所示。其中电机控制系统模块的仿真模型如图9所示。

本文所模拟的风力机型号是恒风－HF4.0.2，具体参数:额定功率PN为2 kW，桨叶半径R为2 m，额定风速VN为8 m/s，额定转矩TN为60 N·m。

所选的电机模型参数:额定电压220 V，额定频率50 Hz，定子电阻 Rs为0.453 Ω，转子电阻 Rr为0.816 Ω，转子漏感 Llr为 0.004 mH，定子漏感 Lls为0.004 mH，定转子自感Lm为0.069 mH，极对数为2，逆变器的直流电压为510 V。转矩调节器ATR设置如表1所示。

表1 转矩调节器ATR设置Tab.1 torque controller settings ATR

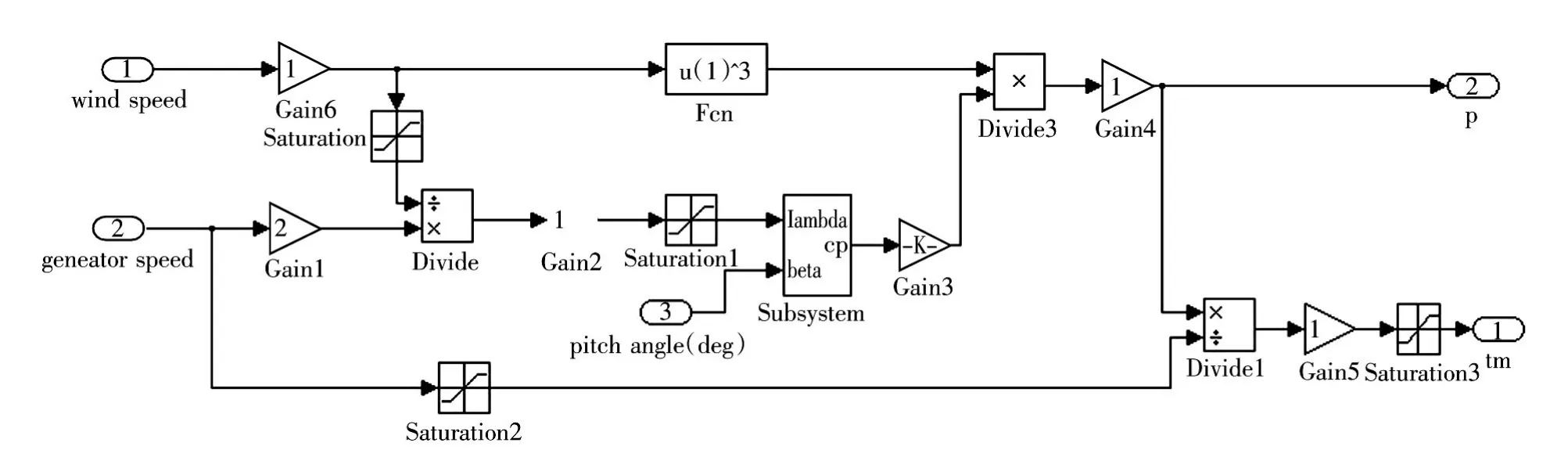
图8 风力机仿真模型Fig.8 Wind turbine simulation model

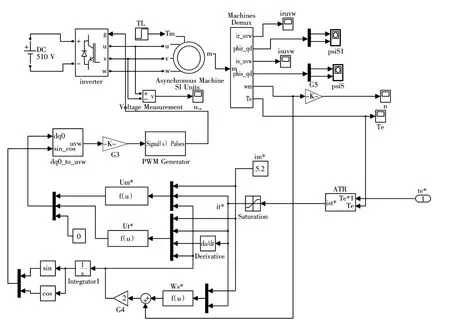
图9 电机控制系统仿真模型Fig.9 Motor control system simulation model

定风速为8 m/s下，控制电机转速逐步增加，电机输出转矩如图10所示。从图10中可以看到，在定风速下，随着转速的增加，叶尖速比相应增加。输出转矩由小到大增长，达到一个峰值，随后由大到小减小，直至为零。其中输出转矩达到峰值时，对应的叶尖速比接近风力机的最佳叶尖速比。可见对电机加以一定的控制，其输出转矩或功率特性基本达到了模拟风力机特性的效果。

在不同风速下，电机输出转矩与转速的关系曲线如图11所示。从图11中可以看到，其关系基本符合风力机的输出特性，达到了本次实验对电机控制模拟风力机特性的目的。但是由于异步电机的特性，以及本文对电机控制采取的策略，在仿真环境下仍有少部分的波动。特别是在给定风速较低情况下，控制效果较不理想，所以更为先进的控制策略有待于近一步的研究。

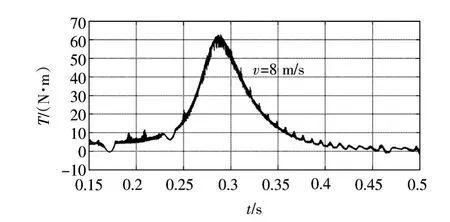
图10 定风速8 m/s输出转矩Fig.10 Constant wind velocity as 8 m/s output torque

图11 不同风速下输出转矩与转速的关系Fig.11 Relation between output torque and speed under different wind speeds

［1］ 刘其辉，贺益康，卞松江.变速恒频风力发电机空载并网控制研究［J］.中国电机工程学报，2004，24(3):6 －11.LIU Qihui，HE Yikang，BIAN Songjiang.Study on the no － load cutting－in control of the variable－speed constant－frequency(VSCF)wind power generator［J］.Proceedings of the CSEE，2004，24(3):6 －11.

［2］ 张琦玮，蔡旭.基于直流电动机的风力机特性模拟［J］.计算机仿真，2007，24(10):276 －344.ZHAGN Qiwei，CAI Xu.Simulation of the characteristic of wind turbine based on DC machine［J］.Computer Simulation，2007，24(10):276－344.

［3］ 刘其辉，贺益康，赵仁德.基于直流电动机的风力机特性模拟［J］.中国电机工程学报，2006，26(7):134 －139.LIU Qihui，HE Yikang，ZHAO Rende.Simulation of the characteristic of wind turbine based on DC machine［J］.Proceedings of the CSEE，2006，26(7):134－139.

［4］ 姚春光，潘卫明，徐殿国，等.基于鼠笼式异步电机的风机模拟实验平台研究［J］.电力电子技术，2010，44(6):24 －25.YAO Chunguang，PAN Weiming，XU Dianguo，et al.Development of experimental platform for wind power generation using induction machine［J］.Power Electronics，2010，44(6):24 －25.

［5］ 乔明.采用异步发电机的风力发电系统研究［D］.北京:北京交通大学，2008.QIAO Ming.Research on wind power system with induction generator［J］.Beijing:Beijing Jiaotong University，2008.

［6］ 焦华.基于异步电动机的风力机模拟系统研究［D］.北京:华北电力大学，2012.JIAO Hua.Research on experimental wind power system based on induction generator［D］.Beijing:NCEPU，2012.