基于磁滞回线数学模型的变压器励磁电流分析
刘 康,程汉湘,郭有翠,朱贵辽
(1.广东工业大学,广州 510006;2.中山市凯丰电力电子设备有限公司,广东 中山 528400)
变压器是电力系统中的重要设备,它的安全性和稳定性对整个电力系统的运行具有相当的重要性。因此,对变压器在合闸时产生的励磁涌流及直流偏磁影响下的励磁电流的分析,是学者们一直重点研究的方向。励磁涌流实际上就是在铁芯绕组所施加的电压突然出现大幅度变化时,在绕组铁芯中引起的电场急剧变化,导致铁芯中的众多磁偶极子发生快速偏转,以及磁场产生快速改变,磁场变化速率越高,则对应的磁势越大;而磁势越大,对应的绕组励磁电流也越大,即产生了励磁涌流。绕组中存在的直流电流会使变压器铁心中存在相应的直流磁动势和直流磁通,直流磁通与交流磁通相叠加,造成铁心的迅速饱和,从而对变压器和电网运行性能产生严重的危害[1]。因此,从铁磁材料的磁滞轨迹出发去研究相关问题,对分析解决问题具有重要意义。
近年来,众多学者对变压器B-H曲线的确定提出了许多方法。文献[2]提出了用高阶多项式拟合磁滞回线;文献[3]提出了基于样条曲线的磁滞回线的拟合方案;文献[4]和文献[5]分别提出了标准磁滞回线的测量方法和直流偏磁条件下磁滞回线的测量;文献[6]和文献[7]则分别采用Pspice和MATLAB仿真软件对磁滞回线进行建模仿真。但是这些方法大多是采用数据拟合,并没有针对磁滞回线的性质提出一种通用模型,具有一定的局限性。本文在经典Preisach模型基础之上,得到了一种的磁滞回线数学模型,通过修改模型相关参数,可以用于描述大多数铁磁材料的磁滞回线。
1 磁滞回线的编程实现
1.1 磁滞回线数学模型[8]
20世纪70年代,俄国数学家Krasnoselskii首先将磁化材料的磁化特性问题归结到数学模型的建立层面,抛开模型的物理意义,将其表达成类似谱分析算子式的纯数学形式。这样就形成了用于描述任何物理滞后现象的新的数学思想。与此同时,Krasnoselskii的数学理论也更深刻地揭示了Preisach模型的现象本质,形成了经典的 Preisach模型[9-11](CPM,Classic Preisach Model)。标准磁滞回线如图1所示。
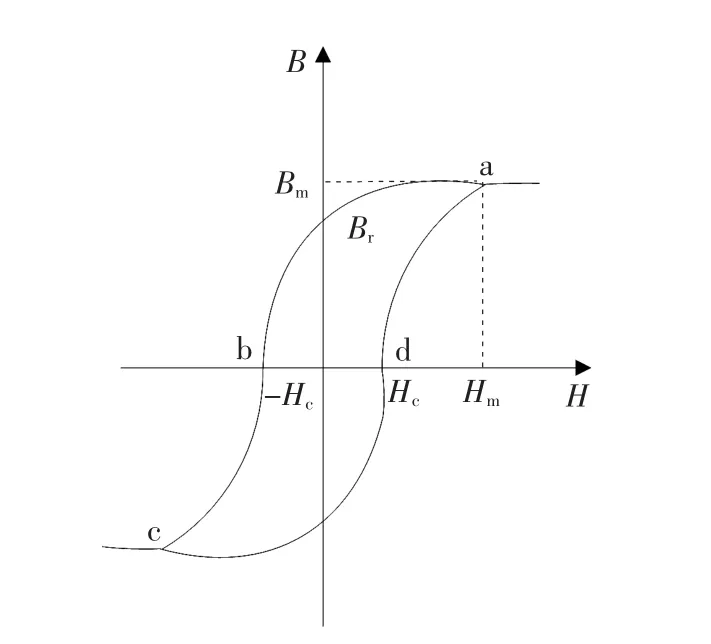
图1 标准磁滞回线Fig.1 Standard hysteresis loop
在图1中,磁滞回线可分为上升段即cda段,下降段abc段,交点分别为(-Hm,-Bm)和(Hm,Bm)。该磁滞回线的数学模型可表示为
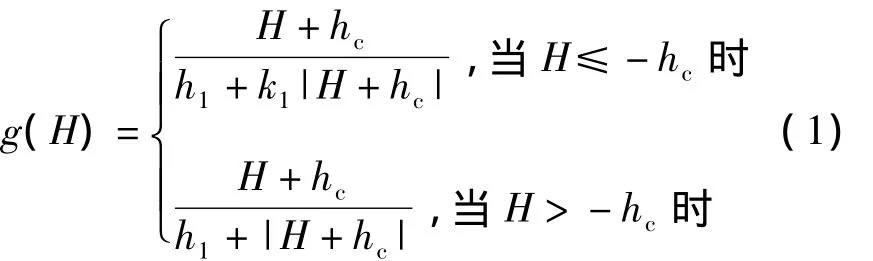
在式(1)中,k1<1,hc可由矫顽力Hc确定的相关参数,可令hc=Hc。整个回线的形状取决于铁磁材料的饱和点(Hm,Bm),在整个(-Hm,-Bm)区间上的下降段曲线可用式(2)表示为
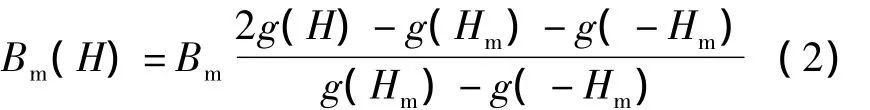
当H=0时,得到的Bm(0)即是所对应的剩磁大小。由于磁滞回线的对称性,上升段的表达式可由Bm(-H)得到。通过调整式(1)、式(2)中的hc、h1和k1三个参数,可得到任意的软磁和硬磁材料的磁滞回线。要想得到直流偏磁条件下的磁滞回线;在程序中加入一个假设的偏磁量,分别对上下段曲线进行修正,可得出直流偏磁条件下大致的磁滞回线。
1.2 磁滞回线编程实现
由VC++实现该回线编程,按文献[8]提供的参数进行设置,Bm=1.7,Hm=500,hc=70,k1=0.8,h1=30,以 H 的在[-Hm,Hm]区间上的变化作为输入变量,将程序所得数据生成.dat文件,并使用MATLAB调用数据显示得到B-H的曲线,即磁滞回线。标准磁滞回线如图2所示;在上述模型的基础之上,假定一个偏磁量ΔB=0.5,得到的具有偏磁影响的磁滞回线如图3所示。
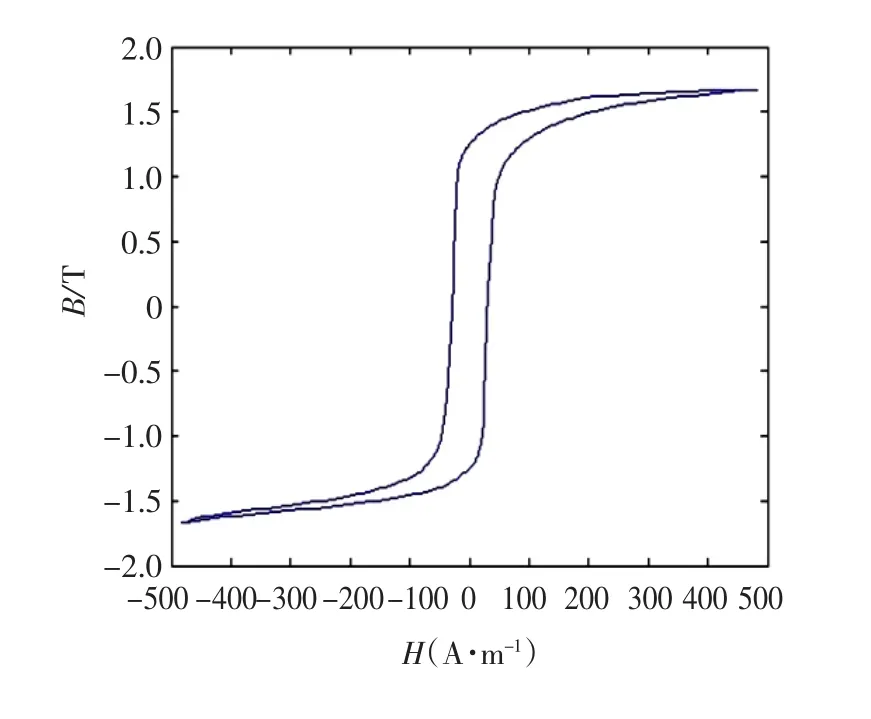
图2 无偏磁量时编程所得磁滞回线Fig.2 Hysteresis loop obtained by programming at unbiased magnetic amount
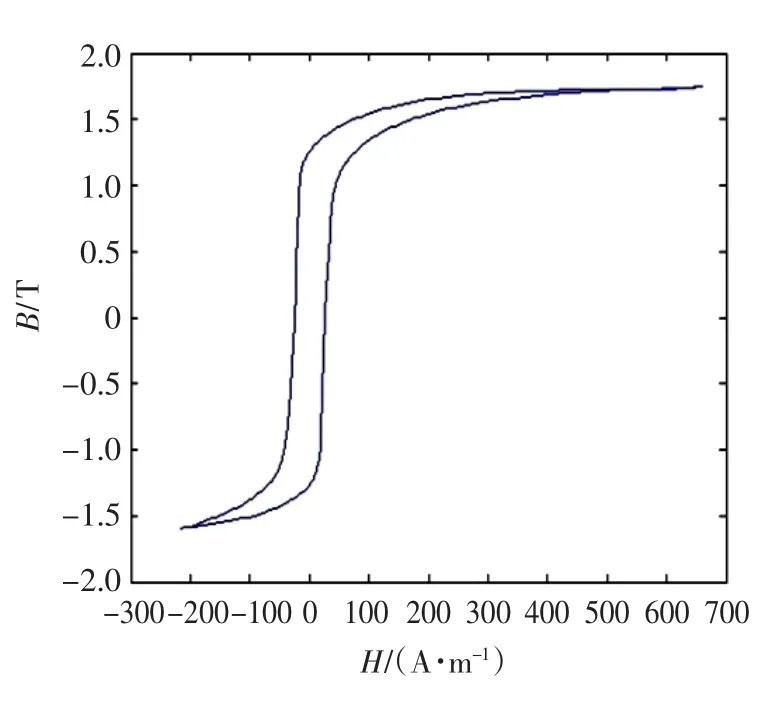
图3 有偏磁量时编程所得磁滞回线Fig.3 Hysteresis loop obtained by programming at biased magnetic amount
由图2、图3可知,由该模型得到的磁滞回线与实际测量结果非常相似,可见该数学模型具有较高的准确性。可用于对变压器励磁涌流进行分析。
2 变压器励磁电流分析
研究工作分为三步,首先,以单相变压器为例,列出所需的磁路与电路方程,然后用VC++语言对方程进行程序编写,最后将所得电流与时间的数据对生成.dat文件。用MATLAB调用数据文件,并对所得结果进行分析。
2.1 编程计算
令变压器二次侧开路,一次侧连接在电压u1=220 V的电网上,则可近似认为e=u1。
根据电磁感应定律

对e进行积分,可得磁通的表达式为

根据磁路定律,可知

式中,S为铁芯的有效截面积。
全电流定律
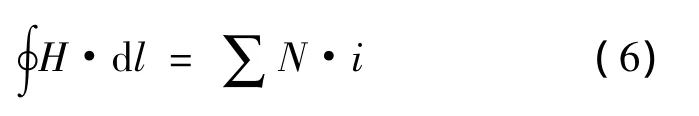
对于每求得的一个H值,其相应的励磁电流为

式中,l为主磁路长度;N为线圈匝数。
只要知道磁场强度H的表达式,便可求得励磁电流。
由式(2)可求得
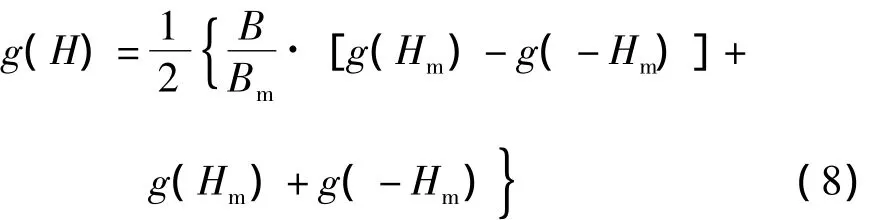
由式(1)可得
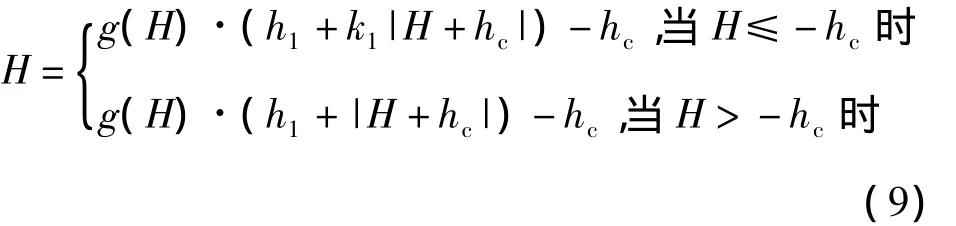
将式(8)带入式(9),则可得到磁场强度 H的表达式

将(10)代入式(7)即可求出励磁电流。由VC++6.0对以上公式编程,第一步首先设置相关参数,其中 Hm、Bm、hc、h1、k1与本文前述设置一致,一次侧电压为220 V,主磁路长度l=1.1460,线圈匝数N=2022,铁芯截面积S=0.025 78,显示周期为0.02 s,总共显示2个周期,频率为50 Hz,步长dt为0.000 05,在考虑偏磁的影响时,先假定一个偏磁量Bdc,求出来对应的励磁电流波形,与理论波形进行对比,验证模型的正确性。假设变压器在t=0时刻合闸,不考虑剩磁的影响。程序流程图如图4所示。
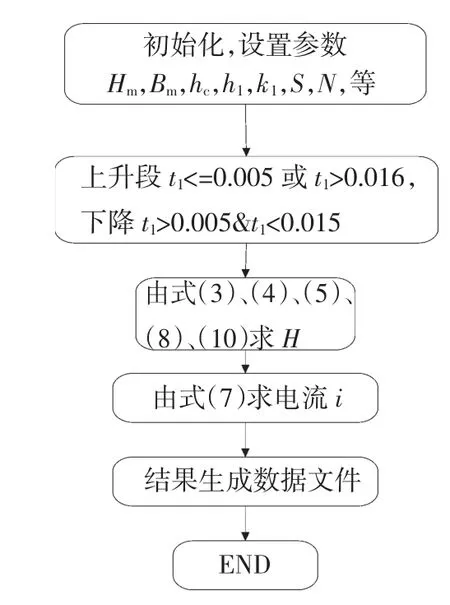
图4 程序流程图Fig.4 Flow chart of program
2.2 结果及分析
将所得的结果生成.dat文件,使用MATLAB调用显示,所得电流波形如图5、图6所示。
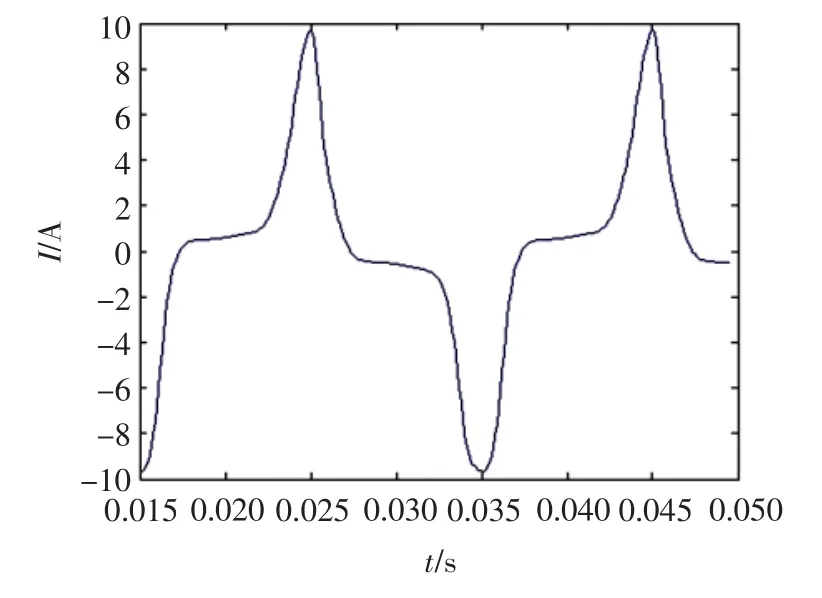
图5 不加偏磁量的励磁电流Fig.5 Excitation current magnetic without biasing magnetic amount
由图5、图6可以看出,由该回线数学模型编程所得到的励磁电流波形与直流偏磁条件下变压器励磁电流的实际波形非常接近,随着偏磁量的增加,变压器的励磁电流畸变越来越严重,并出现严重的半周饱和。
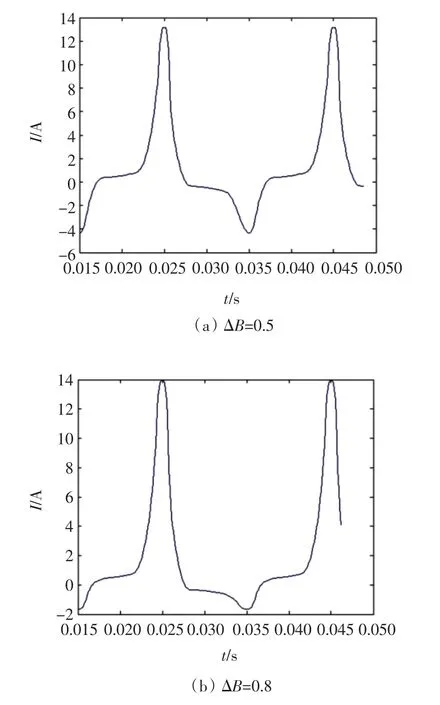
图6 加偏磁量时励磁电流波形Fig.6 Excitation current waveform added bias magnetic amount
3 结语
本文通过对经典Preisach模型进行改进,并修正模型相关参数,得到了直流偏磁影响下的磁滞回线,若将该磁滞回线方程与电路方程相结合,可得到对应的励磁电流波形。用MATLAB仿真软件对其进行验证,得出该模型能正确反映变压器励磁电流实际波形,由此,为解决变压器直流偏磁条件下的励磁电流问题提供了新方法。
[1] 赵小军,李琳,程志光,等.基于直流偏磁实验的叠片铁心磁化特性分析[J].电工技术学报,2011,49(1):7-13.ZHAO Xiaojun,LI Lin,CHENG Zhiguang,et al.Analysis of magnetizing characteristic of laminated core based on the dc-biasing experiment[J].Transactions of China Electrotechnical Society,2011,49(1):7-13.
[2] 张奕雄.高阶多项式在拟合铁磁物质磁滞回线中的应用[J].大学物理,2008,27(2):45-47.ZHANG Yixiong.The application of higher order polynomial in fitting magnetic hysteresis loop[J].College Physics,2008,27(2):45-47.
[3] 陈修芳.基于样条曲线的磁滞回线拟合[J].武汉轻工大学学报,2014,33(1):65-67.CHEN Xiufang.Spline curve fitting for hysteresis loops[J].Journal of Wuhan Polytechnic University,2014,33(1):65-67.
[4] 李都红,张小青,李敬怡,等.一种测量铁磁材料磁滞回线的方法及仿真[J].变压器,2008,45(4):38-39.LI Duhong,ZHANG Xiaoqing,LI Jingyi,et al.Method to measure magnetic hysteresis loop and its simulation[J].Transformer,2008,45(4):38-39.
[5] 王永,刘硕.具有直流偏磁交流磁滞回线的测量[J].磁性材料及器件,2001,47 -50.WANG Yong,LIU Shuo.The measurement of ac hysteresis loop with dc magnetic biasing[J].Journal of Magnetic Materials and Devices,2001,47 -50.
[6] 鲁晓东.铁磁材料磁滞回线的Pspice仿真[J].微计算机信息,2012,28(10):402-403.LU Xiaodong.Pspice simulation on hysteresis loop of ferromagnetic materials[J].Microcomputer Information,2012,28(10):402-403.
[7] 王蕴杰.铁磁材料磁滞回线的MATLAB分析方法设计[J].电脑开发与应用,2012,25(7):51-53.WANG Yunjie.The MATLAB analysis of hysteresis loop [J].Computer Development& Application,2012,25(7):51 -53.
[8] EMAD DLALA.Efficient Algorithms for the Inclusion of the Preisach Hysteresis Model in Nonlinear Finite - Element Methods[J].IEEE trans.Magn,2011,47(2):395 -408.
[9] M L HODGON.Application of a theory of ferromagnetic hystere sis[J].IEEE trans.Magn,1988,24(1):218 -221.
[10] FERENC VAJDA,Edward Della Torre.Minor loops in magnetization dependent Preisach models[J].IEEE trans.Magn,1992,28(2):1245-1248.
[11] D.C.JILES,D.L.ATHERTON.Ferromagnetic Hysteresis.IEEE.Trans.Magn.,1983,19(07):2183 -2185.
[12] W.ROSHEN.Ferrite core loss for power magnetic components design,”IEEE Trans.Magn,1991,27(6):4407 -4415.

