融合频谱变换的板材纹理缺陷分类1)
苏耀文 于慧伶 刘思佳 范德林
(东北林业大学,哈尔滨,150040)
责任编辑:戴芳天。
由于木材生长条件、加工方法的不同,木材表面会形成不同类别的纹理和缺陷。缺陷会降低木材质量,影响木材的使用;纹理直接影响到木制品的视觉美感和经济价值。因此,对板材表面纹理缺陷进行检测对提高商品质量有着重要意义。
图像特征提取方法主要包括结构分析法、统计法、模型法和频谱法。在缺陷检测方面,苏畅[1]等提出了一种基于小波变换和数学形态学的缺陷检测方法,结合阈值处理和区域生长实现缺陷的自动检测。王阿川[2]等结合改进的C-V模型、小波变换和背景填充技术,实现了木材多种缺陷及单板多节子缺陷快速分割。在纹理检测方面,王业琴[3]等提取了纹理的5阶GMRF参数形成最优GMRF参数体系,采用集成神经网络和近邻分类器进行分类识别,取得较高的分类识别率;冯莉[4]等利用遗传算法优选了灰度共生矩阵法和灰度—梯度共生矩阵法的23个纹理特征,得到一组最优纹理特征集;肖淑苹[2]等对彩色图像进行树形结构小波分解,利用支持向量机对9类彩色自然纹理图像进行分类。
尽管表面纹理缺陷分类方法较多,但仍然存在以下问题:单一特征提取方法存在不足。结构分析法只适用于规则排列的纹理基元,不能用于板材表面图像的自然纹理缺陷图像;统计法速度慢、效率低;模型法计算量大,模型系数求解有难度;传统小波变换速度快,能够较好地处理点奇异,但不能有效地处理线和曲线奇异,难以表征二维图像复杂的纹理信息[6-7]。上述方法只能实现单一目标的检测分类,没有实现纹理缺陷的快速协同分选。
Donoho[8]等提出第二代曲波变换,与传统小波相比,曲波变换具有各向异性特点,能够准确表示图像边缘信息,提高纹理分类精度。第一代曲波变换需要子带分解、平滑分块、正规化和Ridgele分析等一系列步骤,实现复杂且有较大的数据冗余量,而第二代曲波变换构建了新的紧致框架,减少了数据冗余,提高了计算速度。
Kingsbury提出双树复小波变换(DT-CWT),与小波和曲波相比,双树复小波不仅具有近似的平移不变性和更多的方向选择性,只需较少的小波系数就可以表示图像信息,而且保留了传统小波的支集,能够更好地表示缺陷特征[9]。
本研究融合小波、曲波和双树复小波变换各自的优点,针对板材表面存在的乱纹、抛物纹和直纹3类纹理以及活结、死结2类缺陷,提取图像的有效特征,采用BP神经网络分类器,实现板材表面纹理和缺陷的快速协同分选。
1 特征提取
小波变换速度快,但缺乏方向性,对复杂纹理分类精度低;曲波变换具有各向异性特点,可用于表示板材表面图像的复杂信息,但支集不适用于表示缺陷特征;双树复小波变换具有多方向选择性,保留了小波支集,能够更准确地表示缺陷信息。分别提取样本图像的小波特征、曲波特征和双树复小波特征,结合3种频谱变换方法的优点进行特征融合,提高分类的速度和精度。
1.1 小波变换
小波变换是一种多分辨率分析的方法,是时间和频率的局部化分析,联合时间—尺度函数,通过伸缩和平移等运算对信号进行多尺度细化分析,特别适用于处理非平稳信号。对一幅图像进行一级小波分解可得到4幅子图:LL、LH、HL、HH,进行下一级小波分解则是将LL子图递归分解为下一个尺度空间的4个分量:LL1、LH1、HL1、HH1,如图1所示。
文献[10]指出Symlets小波系时域和频域的局部化能力强,并且具有较好的对称性,其中sym8小波的尺度函数∅(t)和小波函数ψ(t)能够满足时频分辨率的综合要求。采用sym8小波基对图像进行二级分解后得到7个子图,按照式(1)、式(2)分别求取每个子图的均值和标准差,得到小波变换的14个特征参数。

式中:N为小波分解后的子带数量,i=1,2…,N。
1.2 曲波变换
连续曲波变换是通过环形方向窗 将频域光滑地分割成不同角度的环形,如图2所示。对图像处理时需采用曲波变换的离散形式,为了适应图像的二维笛卡尔坐标系,采用同中心的方块区域 来代替环形方向窗,如图3所示。

图2 连续曲波变换分块图

图3 离散曲波变换分块图
定义笛卡尔坐标系下的局部窗为

Φ被定义为一维低通窗口的内积,满足
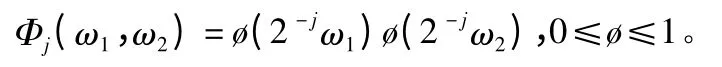
引入相同间隔的斜率
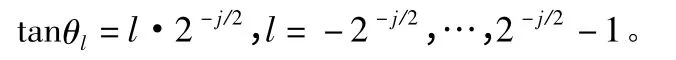
则局部窗被分割为一系列楔形窗,可重新定义~Uj为

式中:Sθ表示剪切矩阵
从而可得到离散曲波变换定义为

式中:b取(k1×2-j,k2×2-j/2)内的离散值。
由于楔形窗不是标准的矩形,不能直接采用快速傅里叶变换,将上式改写为式(4),就可以利用局部傅里叶基得到离散曲波变换系数c(j,k,l)。
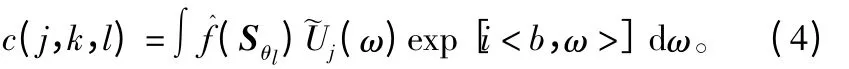
文献[11]提出了两种离散曲波变换算法,分别是usfft算法和wrap算法,本研究采用usfft算法,具体步骤如下:
④进行二维IFFT得到离散的曲波变换系数c(j,k,l)。
经过离散曲波变换后得到图像由内至外的Coarse、Detail、Fine层系数[12]。Coarse层是低频系数,反映了图像的概貌信息;Detail层主要包含边缘特征,是中高频系数;Fine层反映了图像的高频轮廓信息[13]。文献[14]指出Detail层系数对纹理方向性有更好的体现,能够更加准确地表征纹理信息。对Detail层中的第二层系数进行分析,计算第一方向和第二方向中的奇数小方向上的8个系数矩阵的均值和标准差,得到曲波变换的16个特征参数。
1.3 双树复小波变换
一维双树复小波的定义式为

式中:ψh(t)、ψg(t)分别为正交或双正交的实小波,且形成希尔伯特变换对,即满足:

双树复小波变换采用两棵并行的小波树结构,一维DT-CWT变换如图4所示。其中树A产生实部的尺度系数与小波系数,树B产生虚部的尺度系数与小波系数,h0、h1分别代表树A的低通滤波器和高通滤波器,g0、g1分别代表树B的低通滤波器和高通滤波器。并行的小波树结构效率更高,上下两个通道滤波器组之间没有数据上的交互,在硬件和软件上都容易实施。
在分解的过程中,树A、树B交替使用奇偶正交滤波器,对信号进行互补采样,减少了传统离散小波变换由于严格二抽样造成的走样,因此双树复小波具有近似的平移不变性。传统的二维离散小波只能区分水平、竖直和对角方向,如图5(a)所示;而图像经过双树复小波分解后能得到1个低频子带和6个方向的高频子带,分别为±15°、±45°和±75°,具有更多的方向选择性,如图5(b)所示。对图像进行3级双树复小波变换,每一尺度下有6个方向,得到低频子带和18个高频子带,计算各子带系数矩阵的均值和标准差构成图像的双树复小波特征。

图4 一维双树复小波变换

图5 DT-CWT和传统离散小波的比较
2 特征选择
融合图像的小波特征、曲波特征和双树复小波特征,由于这些特征均来自图像频谱变换后的高、低频信息,特征参数之间存在冗余。本研究采用粒子群算法对融合后的特征进行优选,减少特征冗余,提高分类速度和精度。
粒子群算法是一种全局搜索方法,通过群体中粒子之间的信息共享,不断更新粒子最优位置和群体最优位置来寻找最优解。
算法框架如下:
①初始化粒子群,随机对粒子的初始位置和初始速度进行0,1编码。
②计算适应度,以样本的平均分类正确率作为适应度。
③比较粒子在新位置的适应度和它经历过的最优位置pb的适应度,如果更好,则更新粒子最优位置。
④比较粒子的适应度和群体经历过的最优位置pg的适应度,如果更好,则更新群体最优位置pg。
⑤按照式(5)、式(6)分别更新粒子的速度和位置,d表示维数;

⑥当达到设定适应度或最大迭代次数时结束。将得到的群体最优位置pg转换为对应的特征子集:1表示该特征被选中,0表示该特征没被选中。
3 结果与分析
采用BP神经网络作为板材纹理缺陷分类器。BP神经网络是一种信号前向传递,误差反向传播的网络。一个典型的BP神经网络包括输入层、隐含层和输出层,输入层神经元数量n等于特征向量的维数,输出层神经元数量m等于样本类别数量,一个3层神经网络能够以任意精度逼近任何非线性连续函数。输出编码如下:乱纹00100、抛物纹00010、直纹00001、活结10000、死结01000。
实验采用板材样本材料为柞木,摄像头选用Oscar F810C IRF,光源为双排LED平行光源,计算机主频1.6 GHz,实验平台为MATLAB2010b。对300幅表面含有乱纹、抛物纹和直纹3类纹理以及活结、死结2类缺陷的柞木板材表面图像进行分类识别,各样本图像如图6所示。每类样本各60幅,其中30幅作为训练样本,其余30幅作为测试样本。

图6 样本图片
具体分类方法如下:
①对训练图像和测试图像进行灰度化处理,尺寸统一设定为128×128。
②按照式(7)、式(8)计算整幅图像的标准差σ和熵e。分别对图像进行小波变换、曲波变换和双树复小波变换,按照式(1)、式(2)计算各子带系数矩阵的均值和标准差,与σ和e分别构成图像的小波特征、曲波特征和双树复小波特征。

③按照式(9)分别对小波特征、曲波特征和双树复小波特征进行归一化处理,使数据分布在[0.1,0.9]区间内。

④构建BP神经网络,分别用小波特征、曲波特征、双树复小波特征以及3种融合特征,输入神经网络进行训练,输入层函数选用tansig函数,输出层函数选用logsig函数,训练函数选用trainlm函数,误差门限为1.0×10-5。
⑤将测试样本的特征向量送入训练好的BP神经网络进行分类,得到最后的分类结果。
3.1 小波变换分类
利用sym8小波基对原始图像进行二级分解,得到7个子图的14个特征参数。对板材表面图像进行纹理缺陷协同分选,3次实验的分类正确率见表1,平均分类时间0.018 s。

表1 小波变换分类结果 %
针对三类纹理,小波变换的直纹分类精度明显高于乱纹和抛物纹,说明由于缺乏方向性,小波变换对于复杂纹理的表示效果不理想。小波变换对直纹、活结和死结的分类平均正确率较高,对乱纹和抛物纹的分类平均正确率较低,说明小波的支集更适用于直纹和缺陷的表示。
3.2 曲波变换分类
对于尺寸为128×128像素的图像进行曲波变换,划分层次为4层,得到曲波变换的16维特征向量。利用BP神经网络进行分类,结果见表2,平均分类时间为0.503 s。

表2 曲波变换分类结果 %
曲波变换纹理分类正确率比小波变换要高,说明曲波变换能有效表示图像的边缘信息,更准确地表示纹理特征。但是由于曲波的支集是矩形,小波的支集是圆形,使曲波变换对缺陷的分类能力不如小波。
3.3 双树复小波变换分类结果
对图像进行3级双树复小波分解,分类结果见表3,平均分类时间为0.021 s。
由于双树复小波具有更多的方向选择性,使它对纹理的分类能力高于小波变换。双树复小波是由两棵并行的小波树构成,其支集与小波相同,更适合表征缺陷特征,使双树复小波变换的缺陷分类精度高于小波和曲波变换。
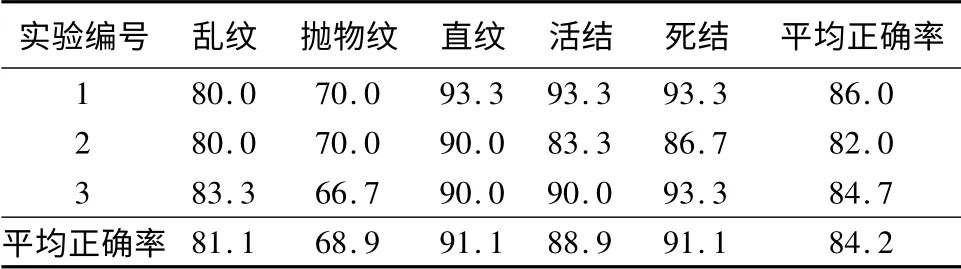
表3 双树复小波变换分类结果 %
3.4 特征融合分类
由于曲波变换具有各向异性,曲波变换的纹理分类精度较高,但是运算时间长。小波和双树复小波的支集更适合表示缺陷的形状,因此缺陷分类精度更高。对比表1、表2和表3,小波和双树复小波对于乱纹的分类能力高于抛物纹,而曲波变换对于抛物纹的分类精度更高。
本研究结合小波、曲波和双树复小波各自的优点,融合三者特征以及原始图像的标准差和熵,得到70维特征向量。为降低特征冗余性,提高分类速度和精度,采用粒子群算法对70维特征向量降维,特征优选结果见表4,对应各项分类结果见表5。

表4 特征优选结果

表5 融合特征分类结果 %
实验结果表明,特征融合后的分类正确率高于小波变换、曲波变换和双树复小波变换;特征维数降低,因而特征提取时间减少。实验2的适应度最高,特征维数最小,分类时间为0.325 s,明显优于曲波变换的分类时间,因此选择实验2的特征编码作为特征选择结果。
与文献[15]的基于空间灰度共生矩阵分类方法进行对比试验,提取均值和、方差和、角二阶矩、对比度和相关度,共5个特征参数。本方法运算时间为0.325 s,灰度共生矩阵法运算时间为1.231 s,分类的平均准确率结果见表6。实验表明,融合方法分类精度更高,且分类时间明显低于灰度共生矩阵方法。

表6 对比结果 %
4 结论
采用频谱变换方法,融合小波变换、曲波变换和双树复小波变换的优点,针对板材表面存在的乱纹、抛物纹、直纹、活结和死结,实现了纹理和缺陷的快速协同分类。研究发现,小波变换速度快,对缺陷分类精度好,但是缺乏方向性,对乱纹和抛物纹分类精度较低;曲波变换的纹理分类精度较高,但是特征计算速度慢,分类时间长;双树复小波保留了传统小波支集,能够准确表示缺陷特征。融合小波特征、曲波特征和双树复小波特征,实现了对三者特征的有效选择,提高了分类的速度和精度。
[1]苏畅,陈宇拓,喻云水,等.基于小波与数学形态学的木材缺陷检测[J].计算机工程与应用,2008,44(33):246-248.
[2]王阿川,仇逊超.木材缺陷识别新方法:改进C-V模型与小波变换[J].计算机工程与应用,2011,47(8):211-214.
[3]王业琴,王辉.GMRF随机场在纹理特征描述与识别中的应用[J].计算机工程与应用,2011,47(25):202-204.
[4]冯莉,李满春,李飞雪.基于遗传算法的遥感图像纹理特征选择[J].南京大学学报:自然科学,2008,44(3):310-319.
[5]肖淑苹,陈一栋,杨建雄.基于小波变换和支持向量机的彩色纹理识别[J].微电子学与计算机,2010,27(7):117-20.
[6]马莉,范影乐.纹理图像分析[M].北京:科学出版社,2009.
[7]孙延奎.小波变换与图像、图形处理技术[M].北京:清华大学出版社,2012.
[8]Candès E J,Donoho D L.New tight frames of curvelets and optimal representations of objects with C2singularities[J].Commun on Pure and Appl Math,2004,57(2):219-266.
[9]Kingsbury N.Complex wavelets for shift invariant analysis and filtering of signals[J].Applied and Computational Harmonic Analysis,2001,10(3):234-253.
[10]刘明贵,岳向红,杨永波,等.基于Sym小波和BP神经网络的基桩缺陷智能化识别[J].岩石力学与工程学报,2007,26(增1):3484-3488.
[11]毕杨,肖军.基于快速曲波变换和独立分量分析的有噪图像盲分离算法[J].自动化技术与应用,2010,29(1):53-56.
[12]张云强,张培林,任国全,等.曲波变换用于磨粒图像不变矩的提取[J].中国图象图形学报,2012,17(2):263-268.
[13]李晖晖,郭雷,刘坤.基于曲波变换的遥感图像融合研究[J].光电子·激光,2008,19(3):400-403.
[14]张怡卓,马琳,许雷,等.基于小波与曲波遗传融合的木材纹理分类[J].北京林业大学学报,2014,36(2):119-124.
[15]王晗,白雪冰,王辉.基于空间灰度共生矩阵木材纹理分类识别的研究[J].森林工程,2007,23(1):32-36.

