小波包多阈值法在地震信号去噪中的应用研究
刘淑聪,高尔根,陈逊,刘春侠
(防灾科技学院,河北三河065201)
小波包多阈值法在地震信号去噪中的应用研究
刘淑聪,高尔根,陈逊,刘春侠
(防灾科技学院,河北三河065201)
地震信号中通常含有各种干扰噪声,严重影响了地震资料的信噪比和分辨率,小波包变换是地震资料去噪的有效方法之一。针对传统小波包阈值去噪不明显和存在失真的问题,提出一种基于多阈值函数的小波包地震信号去噪方法。对地震波信号进行小波包分解,并对小波包分解系数按照频率大小的顺序进行排列,根据分解的系数处于不同频带选取不同的阈值准则进行去噪处理,对得到的系数进行重构,可有效地去除地震信号中的噪声。对仿真地震信号以及实际地震信号进行小波包多阈值去噪处理,实验结果表明,该方法较好地去除了干扰噪声保留了有用信号,去噪效果明显且失真小,有效地提高了地震资料的分辨率。
地震信号;小波包变换;多阈值函数;信号去噪
0 引言
在地震勘探中,由于地震信号的复杂性,不可避免地要受到各种干扰噪声的影响,使得采集到的原始地震信息剖面模糊不清,地震资料信噪比和分辨率降低,地震资料解释与处理更为困难,因此降噪是地震资料处理的关键。很多学者根据信号和噪声的各种差异,设计了多种去除噪声、提高信噪比的方法[1-2]。小波变换作为一种新方法技术,由于其具有时频分析、多分辨率和去相关性等特点,在信号处理方面得到了广泛应用[3-4]。小波包变换是小波变换的推广,不仅对信号的低频部分进行分解,而且可以对小波分析未分解的高频部分提供更精细的分解,能够对包含中、高频信息的信号进行更好地时频局部化分析。小波包变换是一种更加精细的分析和重构方法,对地震信号中的高频噪声有一定的去噪效果[5-6],但传统的小波包去噪方法没有对信号和噪声的特征进行充分的研究,去噪效果不明显,去噪精度有待进一步提高。
本文提出一种对不同频率成分选择不同阈值函数的小波包地震信号去噪方法,对小波包分解系数按照频率大小的顺序进行排列,根据信号和噪声的分解系数处于不同频带选取不同的阈值准则进行去噪处理,对得到的系数进行重构,可有效地去除信号中的噪声。通过本文小波包多阈值去噪方法对人工合成地震记录以及实际地震信号进行降噪处理,结果表明小波包多阈值地震信号去噪方法能够有效提取信号中各频段的有用信息,消除干扰信号,去噪能力相对于传统方法有所提高,可获得较理想的去噪效果。
1 小波包理论
1.1 小波包分解
在小波分析去噪中实际信号往往被认为由有用信号和噪声组成,经过小波变换后,有用信号的能量主要集中在低频的小波系数上,噪声信号的能量主要集中在高频的小波系数上,因此通常把高频部分去掉(置零),低频部分用于进一步分解和重构,这样就损失了包含在高频段的有用信号。小波包分解是一种比小波分析更加精细的时频分析方法,它可以对小波空间进行进一步分解,能同时对信号的高频部分和低频部分进行多层次划分,具有更为精确的时频局部分析能力,更加有利于信号和噪声的分离。


通常情况下,小波包降噪步骤为[7]:
(1)信号的小波包分解:选择合适的小波基函数并确定小波包分解的层次N,对地震波记录信号S进行N层小波包分解。A表示低频,D表示高频,末尾序号数表示小波包分解的层数,即尺度数。原始信号S经过3层分解后等价于:

(2)计算最佳小波基:根据一个给定的熵标准计算最佳树,常用熵标准有shannon,threshold,norm,log energy,sure和user等几种类型。
(3)小波包分解系数的阈值量化:为有效区分信号和噪声,需对分解的每一个小波包系数选择合适的阈值进行阈值处理。常用的阈值处理方法有强制消噪处理、默认阈值消噪处理、软(或硬)阈值消噪处理。软(或硬)阈值消噪最为常用,但是仍然存在问题。
(4)信号重构:利用经过阈值处理后的小波包系数进行重构即可获得去噪处理后的信号。
1.2 小波包的频率顺序
以N=3为例,信号S经过3层小波包分解后,原始信号S=AAA3+DAA3+ADA3+DDA3+AAD3+DAD3+ADD3+ DDD3。
其中A表示低频,D表示高频,末尾序号数3表示小波包分解层数(尺度数为3),分解结构如图1所示。

图1 小波包3层分解结构图
以noischir信号进行sym6小波3层分解,分解后的各小波包系数如图2所示。通过图2可以发现,小波包系数的自然顺序与其频率顺序不一致,最低频部分对应的是AAA3,其次是DAA3,最高频部分对应的是AAD3。

图2 noischir信号3层小波包分解系数
由文献[8]可知小波包分解后的结果并不是频率由低到高排列,任何小波包都会产生频率顺序错位,由于小波包分解时,高通滤波器会进行一次“翻转”操作,故小波包分解后的低频部分按频率从小到大排列,高频部分按频率从大到小排列。可以通过小波包的性质证明[8],任何小波包的分解都会产生自然顺序与频率顺序不一致的现象,并且不一致现象的情况是一样的。
2 小波包多阈值去噪方法
2.1 最佳小波包基的确定(计算最佳树)
一个长为L=2N的信号最多有2N种不同的分解方法,同时一个深度为N的完全二叉子树的个数为2N。这个数字很大,不可能对每一种情况一一列举,而通过最小熵标准可以得到一种最优的信号分解方法。传统的基于熵的标准有shannon熵、threshold熵、norm熵、log energy熵、sure熵和user熵等几种类型。shannon熵定义如下:

对信号进行逐层分解,分解的每个节点计算熵值,通过比较某一节点与其子节点的熵值,获取熵值最小的基即为最优小波包基。
2.2 多阈值选取
在小波阈值去噪中通常认为噪声表现为高频信号,对小波分解的高频系数进行门限阈值处理,小于阈值认为是由噪声产生的并置零,大于阈值相应于有用信号将其保留,从而实现信号和噪声分离。小波包分解可以对小波分解产生的高频信号进一步分解从而获得高频部分更详细的信息,有助于将高频噪声和高频信号区分开来,从而获得更为理想的去噪效果。经过小波包分解后的小波包系数包含着不同的信息,有用信号和噪声信号,如果对所有的小波包系数采取同一种阈值方法处理,便容易出现去噪效果不明显或是去噪过度等现象影响去噪精度,若对小波包系数分情况进行多阈值函数处理就很好地克服了上述缺点。
多阈值处理就是对每个小波包分解系数灵活地选用不同的阈值准则,从而最大程度地保留有用信号去除噪声信号。在了解了小波包分解系数的频率顺序之后,就可以将小波包分解系数按照频率顺序从小到大排列,从而进行频带分割。根据噪声与信号在各频带上的小波包分解系数的不同表现,采用多个阈值进行去噪。在不同的频带采取不同的阈值处理方法,最后进行信号重构,实现不同频带多阈值去噪处理。
小波包分析中常用的四种阈值准则有固定形式阈值准则(sqtwolog准则)、自适应阈值准则(rigrsure准则)、启发式阈值准则(heursure准则)以及极小化极大阈值准则(minimaxi准则),各自的选取规则不同,适用范围不同,去噪效果也不相同[9]。
(1)固定形式阈值准则(sqtwolog),采用的是固定形式的阈值,产生的阈值大小为sqrt(2⋅log(length(X)))。
(2)自适应阈值准则(rigrsure),基于Stein的无偏似然估计原理的自适应阈值选择。
(3)启发式阈值准则(heursure),是无偏似然估计和固定阈值估计原则的折中。如果按无偏似然估计原则处理的信号噪声很大,在这种情况下就采用这种固定的阈值。
(4)极小化极大阈值准则(minimaxi),采用极大极小原理选择阈值,它产生一个最小均方差的极值,而不是没有误差。
minimaxi阈值准则和rigrsure准则更加保守,不容易丢失信号中的有用成份,但只除去较少的噪声。sqtwolog阈值准则以及heursure阈值准则两种方法类似,都是将全部系数进行处理,因此可以较强地去除噪声,但是也容易引起过度去噪使信号失真。因此,本文采用小波包多阈值处理,将分解后的系数分为不同的频带,中低频部分采用minimaxi阈值准则和rigrsure阈值准则,而在高频部分采用sqtwolog阈值准则以及heursure阈值准则。阈值准则选取之后可对每层的系数进行噪声层的估计来调整阈值。
2.3 算法步骤
(1)根据所给信号选定一个合适的小波基函数,先对信号进行N层小波包分解,获得与树T节点N对应的系数cfi(i=0,1,2,…),并按频带进行排序。
(2)优化小波包树,确定熵标准从而选定最优小波基,得到最优树。
(3)依据信号获取sqtwolog准则对应的阈值th1,rigrsure准则对应的阈值th2,heursure准则对应的阈值th3,minimaxi阈值准则对应的阈值th4。
(4)利用不同的阈值对小波包分解的系数cfi(i=0,1,2,…)进行阈值处理,低频段采用阈值th2,中频段采用阈值th4或th1,高频段采用阈值th3。可设定各频段比例系数。
(5)对处理后的小波包系数进行重构。
3 仿真实验
3.1 模拟地震记录去噪
为了验证新阈值函数小波包消噪的有效性,对一段加入随机噪声的模拟地震信号进行试验,信号的长度为1 000,图3是对含噪声的模拟地震记录处理对比图。其中图3(a)为模拟地震信号,信噪比为7 dB,图3(b)为小波包硬阈值去噪后的信号,图3(c)为小波包软阈值去噪后的信号,采用小波包分解时,选取“dB2”小波基,最大分解尺度为3。图3(d)为小波包多阈值方法去噪后的信号。
为了比较不同阈值降噪方法的降噪效果,选用均方根误差(RMSE)、信噪比(SNR)为评价指标用来定量比较去噪效果,如表1所示。将原始信号记为f(n),含噪信号为s(n),信号长度为L,信噪比(SNR)公式定义为:
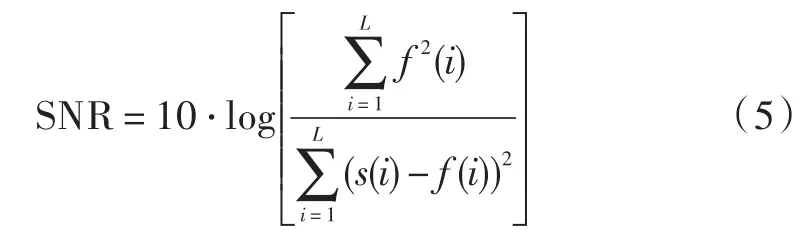
原始信号与估计信号之间的均方根误差(RMSE)定义为:
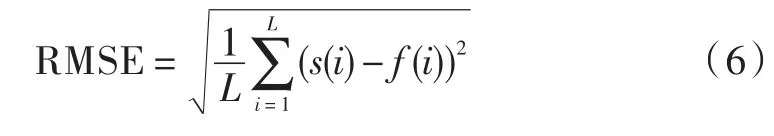
其中均方根误差越小、信噪比越大则去噪效果越好。

图3 模拟地震信号去噪

表1 模拟记录各种方法去噪效果比较
从图3和表1中可以看出,以上的几种方法去噪后信噪比都有所提高,大部分噪声都得到了抑制,但是使用小波包多阈值法去噪后,失真最小,信噪比(SNR)和均方根误差(RMSE)最大,去噪效果最好。
3.2 合成地震剖面去噪
在Matlab下可仿真合成地震剖面,通常采用一个低频ricker子波和一个高频ticker子波叠加合成共炮点道集[10],设置参数深度为100 m,最小偏移距为10 m,道数为50。图4为合成的共炮点道集,图5为加入20 dB随机噪声后的共炮点道集。采用sym4小波进行小波包去噪,图6是小波包硬阈值去噪后的共炮点道集,图7是小波包软阈值去噪后的共炮点道集,图8是小波包多阈值法去噪后的共炮点道集。从图6~图8可以看出,采用小波包多阈值方法去噪后噪声有效地减小,相比常规小波包阈值去噪方法,失真小,去噪后的地震信号最接近于原始信号。从表2中可以看出,经过小波包硬阈值去噪、小波包软阈值去噪和小波包多阈值去噪后的信噪比分别为36.700 6 dB,35.430 9 dB和39.974 6 dB,采用小波包多阈值方法去噪的信噪比最高,效果最好。
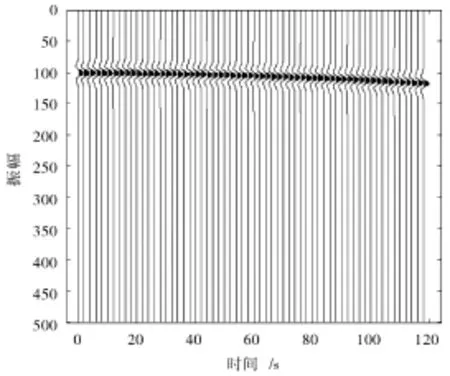
图4 合成的共炮点道集

图5 加入噪声后的共炮点道集

图6 小波包硬阈值去噪后的共炮点道集
4 地震资料去噪
实际采集的原始地震数据有大量的噪声,如随机干扰,线性干扰等噪声,这些噪声相互混合影响原始地震数据,使整个地震剖面分辨率较低,必须对采集的数据进行消噪处理。实验在某地区观测点采用分布式地震仪进行观测,26通道,道间距为1 m,偏移距为10 m,炮点距(两炮点间距离)为2 m,检波器阵列与震源阵列共线,地震仪采样率为8 kHz,记录时间为6 s。对采集到的实际地震信号选用sym4小波进行3次分解。

图7 小波包软阈值去噪后的共炮点道集

图8 小波包多阈值去噪后的共炮点道集

表2 地震剖面各种方法去噪效果比较
4.1 单通道地震信号去噪
图9(a)为其中的一个通道实际信号中的一部分数据,图9(b)为小波包软阈值去噪后的信号,图9(c)为小波包硬阈值去噪后的信号,图9(d)为小波包多阈值去噪后的信号。
从图9(b)和图9(c)可以看出硬阈值函数去噪和软阈值函数去噪后的地震信号都去除了一定的噪声,但去噪效果不明显。经过本文小波包多阈值函数去噪后的地震信号如图9(d)所示,滤除了大部分噪声,有用信号分量却很好地保留下来,失真较小,去噪效果最好,经过小波包多阈值函数去噪后的地震信号也最接近于原始信号。
图10分别为实际信号及三种方法去噪后的信号频谱图,从图中可以看出信号的主要频率在20 Hz和60 Hz左右,经过去噪后噪声都有所压制,但小波包多阈值法去噪后的有用信号得到增强,噪声得到了更好地压制,可以看出其去噪效果最好。

图9 单通道地震信号去噪处理

图10 单通道地震信号去噪频谱图
4.2 多通道地震信号去噪
图11(a)为26通道部分实际地震信号,经过小波包多阈值函数去噪后如图11(b)所示,从图中可以看出信号中的噪声大部分已被消除,有用信号很好地保留,同相轴更加清晰。图11(c)和图11(d)分别为从图11(a)和图11(b)中取0~300 ms区间内的部分波形,可发现26通道实际地震信号主要集中在该区间,从图11(d)中也可以发现噪声被较好地去除,有用信号增强,同相轴更加清晰。
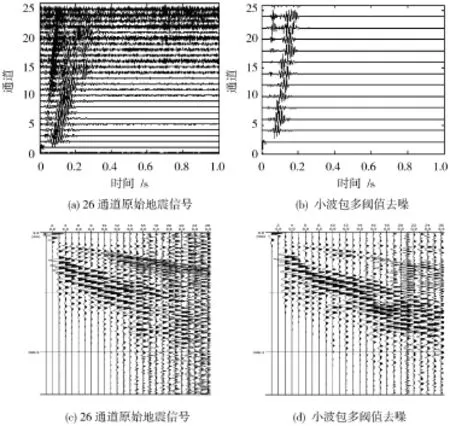
图11 多通道地震信号去噪
5 结语
本文提出一种基于小波包多阈值函数的地震信号去噪方法,将信号经过小波包分解后的系数按照频率大小的顺序排列,在不同频段范围内选取合适的阈值方法进行自适应阈值处理。理论分析和实际地震信号应用表明该方法能够对信号按不同频段进行去噪处理,既能有效地去除低频中的噪声,又很好地保留了高频中的有用信号,有效地解决了其他方法去噪效果不明显或过度去噪的问题,可提高地震资料的信噪比和分辨率,可应用于实际地震资料的处理中。
[1]张军华,吕宁,田连玉,等.地震资料去噪方法技术综合评述[J].地球物理学进展,2006,21(2):546-553.
[2]刘霞,潘洪屏,高晓春,等.基于小波阈值的地震信号去噪处理[J].科学技术与工程,2010,10(29):7251-7254.
[3]裴正林.小波理论及其在地震数据处理中的应用[J].地球物理学进展,2002,17(3):486-490.
[4]吴招才,刘天佑.地震数据去噪中的小波方法[J].地球物理学进展,2008,23(2):493-498.
[5]张瑞红,林大超,乔兰.最优小波包变换在地震信号去噪中的应用[J].地震研究,2011,34(3):358-363.
[6]周怀来,李录明,李枚,等.基于小波包分析的地震资料联合去噪方法研究[J].物探化探计算技术,2007,29(5):391-395.
[7]胡昌华,李国华,周涛.基于Matlab 7.x的系统分析与设计:小波分析[M].3版.西安:西安电子科技大学出版社,2008.
[8]纪跃波.小波包的频率顺序[J].振动与冲击,2005,24(3):96-98.
[9]章浙涛,朱建军,匡翠林,等.小波包多阈值去噪法及其在形变分析中的应用[J].测绘学报,2014,43(1):14-20.
[10]刘霞,潘洪屏,高晓春,等.基于小波阈值的地震信号去噪处理[J].科学技术与工程,2010,10(29):7251-7254.
[11]赵志刚,万娇娜,管聪慧.基于小波包变换与自适应阈值的图像去噪[J].中国图象图形学报,2007,12(6):977-980.
[12]DUHAMEL P.Algorithms meeting the lower bounds on the multiplicative complexity of length-2nDFTs and their connection with practical algorithms[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1990,38(9):1504-1511.
Application of wavelet packet multi-threshold method in seismic signal denoising
LIU Shucong,GAO Ergen,CHEN Xun,LIU Chunxia
(Institute of Disaster Prevention,Sanhe 065201,China)
Since the seismic signal generally contains a variety of interference noises,which affects the signal-to-noise ratio and resolution of seismic data seriously,and because the wavelet packet transform is an effective way of the seismic signal denoising,a seismic signal denoising method based on wavelet packet of multi-threshold function is proposed for the traditional wavelet packet threshold denoising method has unobvious denoising effect and distortion.The wavelet packet decomposition is conducted for seismic wave signal,and the wavelet packet decomposition coefficients are arranged according to the frequency real values.Different threshold criterions are selected to conduct denoising processing according to the decomposed coefficients in different bands to reconstruct the obtained coefficients,which can eliminate the noise in seismic signal effectively.The denoising processing of wavelet packet multi-threshold for the simulation seismic signal and practical seismic signal were conducted.The experimental results show this method can eliminate the interference noise availably while reserving the useful signal,has good denoising effect and low distortion,and can improve the resolution of seismic data efficiently.
seismic signal;wavelet packet transform;multi-threshold function;signal denoising
TN911.7-34;TH763
A
1004-373X(2015)23-0054-06
10.16652/j.issn.1004-373x.2015.23.016
刘淑聪(1983—),女,河北燕郊人,讲师,研究生。主要研究方向为信号处理。
2015-07-20
中国地震局教师科研基金项目(20140105);国家自然科学基金2011年度面上项目(41174043);中央高校基本科研业务经费项目(ZY20110101)

