各向异性砂土剪切带角度的理论分析
李学丰,袁 琪,马文国
(宁夏大学 固体力学研究所,银川 750021)
各向异性砂土剪切带角度的理论分析
李学丰,袁 琪,马文国
(宁夏大学 固体力学研究所,银川 750021)
针对平面应变条件下各向异性砂土剪切带角度的试验规律,采用传统的3种理论和分叉理论进行对比分析。将平面应变条件下剪切带角度的试验结果按照传统3种理论整理发现,尽管传统3种理论可以估算同种砂剪切带角度的极小、中间和极大值,但无法解释其各向异性规律。砂土在平面应变条件下破坏时会产生明显的剪切带,当剪切带方向和砂土沉积面方向接近时,会较早诱发剪切带的产生,使材料强度降低,造成了平面应变条件下各向异性强度规律明显不同于常规三轴条件下的试验规律,采用分叉理论结合各向异性模型则可以有效解释这个规律。随砂土沉积面角度的变化,模型可以从细观角度解释常规三轴条件下剪切带角度的单调变化的试验规律,结合分叉理论可以描述平面应变条件下其先减小然后增大的规律。通过几种理论对比分析表明,模型结合分叉理论不但能够描述多种应力状态下的平面应变和常规三轴应力条件下剪切带角度表现的不同规律,而且能够从细观角度解释其各向异性成因。
剪切带;分叉理论;各向异性;平面应变;细观特性
剪切带是土体变形破坏的常见现象,它直接导致岩土材料强度降低、承载力下降。剪切带与土体的薄弱点或应力集中点有关,在荷载作用下,土颗粒沿该点定向排列,逐步扩展成贯通的破坏带。数学上解释为:可将土体物理特性视为一个复杂的非线性系统,当满足某些临界条件时,土体均匀变形模式发生分叉,取而代之的是不均匀变形模式。
剪切带形成机理一直困扰着岩土工作者。最初Roscoe等[1]的单剪试验把剪切带归因于某种边界条件下的特有现象,与土性无关。后来研究发现:即使改进试验仪器和优化试验方法,也无法避免剪切带的产生,它是特定应力条件下(如平面应变条件下)土体必然出现的破坏形式。而且剪切带形成前后土体的变形机理明显不同,形成前趋于均匀变形,形成后则为剪切带的局部化变形为主。其变形的深层机理与土体细观特性密切相关。
砂土细观特性影响了剪切带形式、厚度和倾角。Nemat-Nasser等[2]对剪切带内外变形的定量研究发现:剪切带中心的剪应变高于带外数十倍,并导致了带内很高的孔隙比;Alshibli等[3]研究表明:剪切带厚度大约为9.6~10.63倍粒径,且随密度增加而增加;Francesco等[4]用三维X射线技术对Ottawa砂分析认为:剪切带厚度约为12~13倍的颗粒直径;剪切带倾角方面,Finno等[5]采用立体摄影技术检测到平面应变条件下饱和松砂剪切带角度约为55°~65°。Vardoulakis等[6]的试验表明:剪切带角度在细砂中为62.5°,中砂中为60.1°;Abelev等[7]用改进的真三轴试验表明:在中主应力系数为0时,没有观测到剪切带,剪切带的形成主要在中主应力系数为0.2~0.8的区间;更难解释的是剪切带各向异性规律,如 Tatsuoka等[8]、Oda等[9]和 Yoshida等[10]诸多学者的大量平面应变试验表明:激光斑纹法观测的剪切带角度表现了明显的各向异性规律,即随砂土沉积面角度在0°~90°范围内的变化,倾角先减小,然后增大。当砂土沉积面方向和大主应力方向夹角为56°~67°,剪切带角度最小,此时沉积面和剪切带的方向接近。这与三轴试验条件下观测到强度单调变化规律完全不同。如果用传统预测理论描述,当沉积面方向和大主应力方向一致时,剪切带角度与 M-C(Mohr-Coulomb)理论值接近;当沉积面方向和大主应力方向夹角为56°~67°,剪切带角度与Roscoe理论接近。平面应变和三轴试验条件下出现了不同规律,相同的试验条件下不同沉积角度试样的剪切带角度需要不同理论解释,这是传统理论描述各向异性剪切破坏规律的难点。
针对以上问题,陈立平等[11]结合砂土细观机理做了研究,宋飞等[12]也做了实验研究。笔者针对砂土剪切带试验规律,基于笔者在砂土宏细观各向异性力学特性[13-14]和应变局部化[15]方面工作,在本文中提出了理论预测砂土剪切带角度的方法,采用传统的M-C理论、Rosco理论和Arthur等理论对各向异性砂土剪切带角度规律进行归纳总结,分析几个理论的特点;然后用基于细观组构张量建立的各向异性模型[15]结合分叉理论预测各向异性砂土剪切带角度,从细观角度解释当砂土沉积面和剪切面接近时,剪切带角度最小的规律。
1 剪切带角度的分叉理论预测
剪切带的各向异性规律需要用各向异性模型描述。有关模型和分叉理论的详细描述见文献[15],本文中只对分叉理论预测平面应变条件下剪切带角度做简要介绍。
岩土材料应力-应变关系普遍的特征如图1所示:加载初期材料处于弹性变形阶段,随着变形的增大材料进入塑性状态,应力随着变形的增大而增大,此时材料处于应变硬化阶段;当塑性变形达到一定程度后,应力达到材料强度值,随着变形的继续增大,应力开始逐渐降低,即材料进入应变软化阶段。从硬化阶段到软化阶段的转变,一般认为是材料变形模式的分叉所造成,转变的临界点即为分叉点。分叉前材料状态相对稳定,分叉后则处于失稳状态,此时应力-应变关系不唯一。
分叉的物理机制材料中的薄弱点与应力集中点有关,在荷载作用下,土颗粒从这些点开始定向排列,逐步扩展形成一个贯穿的剪切带。剪切带产生意味着材料原先均匀变形模式的分叉,使得变形模式不再均匀。在数学上,描述应变局部化的发生条件一般为:在均匀变形场上假设一个附加变形场的存在,当材料受到进一步加载作用时,寻求满足这种附加变形存在和发展的条件,即分叉条件。
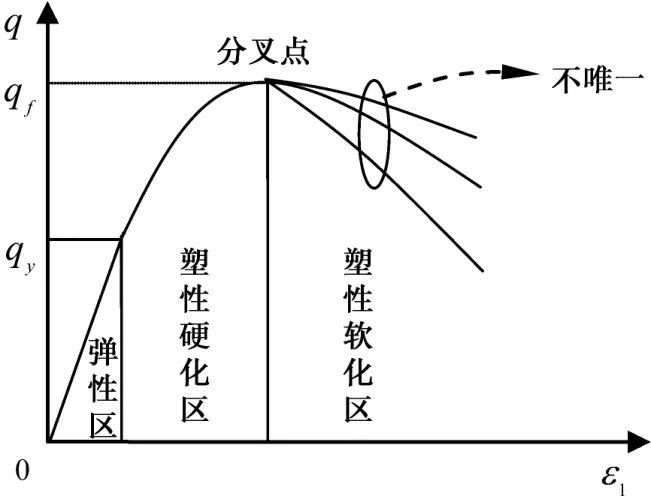
图1 应力-应变关系Fig.1 Stress-strain relations
Valanis[16]认为分叉点对应于材料失稳的极限点,也是判断材料失稳的充分必要条件。极限点对应的应力率为零,切线模量具有零特征值,即

2 剪切带角度的传统理论预测
土力学中,传统剪切带角度判别准则常用的是M-C理论,还有Roscoe理论和Arthur理论。
2.1 M-C理论

式中:φf为土体破坏时的内摩擦角;各向同时,φf是一个常量。如图2,剪切带方向与小主应力σ3方向的夹角为

M-C理论没有考虑中主应力的影响,它是在试验的基础上的一种简单线性假设,应力水平较高时,理论预测与试验结果有偏差。
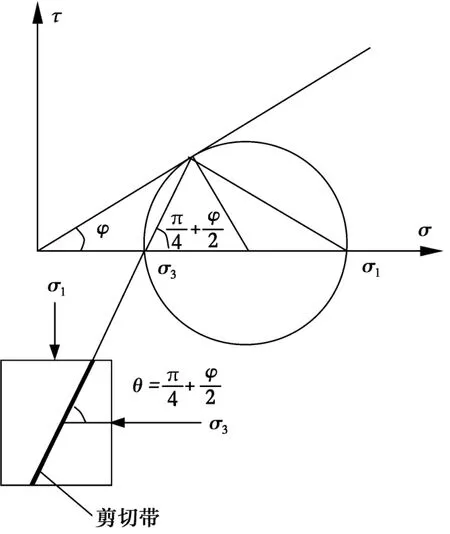
图2 M-C理论破坏面Fig.2 Failure surface of M-C theory
2.2 Roscoe理论
Roscoe等[1]认为土体应变大小与土体破坏密切相关,假设剪切带方向与零伸长方向相同,用Mohr圆表示应变增量,剪切带与主应变轴dε3的夹角为

如图3所示,Roscoe理论确定的剪切带方向实质上是滑移面的方向。相对M-C理论,Roscoe理论强调了应变增量对土体破坏的影响,理论采用剪切带方向平行于零伸长线的假设,没有形成具体的剪切带判别准则。
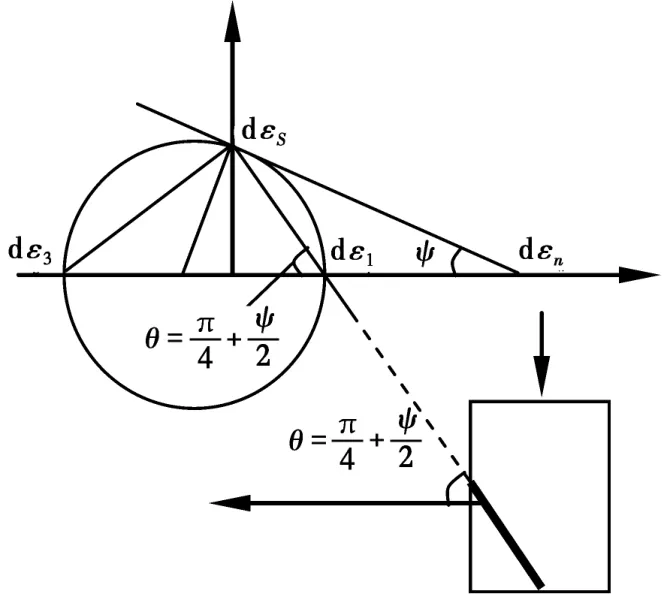
图3 Roscoe理论破坏面Fig.3 Failure surface of Roscoe theory
2.3 Authur理论
在工程实践中,M-C理论预测剪切带角度偏大、偏保守,可作为剪切带的上限值。相反,Roscoe理论的预测值则偏小、不安全,该值可作为剪切带角度的下限值。鉴于上述两种经典理论对剪切带方向预测特点,Authur等[18]建议用两个理论的算术平均值预测剪切带倾角
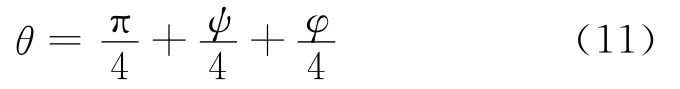
3 剪切带角度的试验结果
图4(a)、(b)分别是 Tatsuoka等[8]和 Yoshida等[10]的平面应变试验结果,试验都清晰地观测到剪切带。

图4 平面应变试验的剪切带Fig.4 Shear bands of Plane strain test
图4中Tatsuoka等[8]用Toyoura重塑砂和天然砂平面应变试验观测到剪切带倾角的规律为:
1)剪切带方向和峰值状态内摩擦角和剪胀角相关且内摩擦角度远远大于剪胀角。
2)竖向沉积的砂土有明显的各向异性,因此剪切带受其沉积方向影响显著,然而理论研究时往往忽略了各向异性的影响。
3)当应力增量轴和应变增量轴发生旋转时,它们的增量方向不相同,表现为非共轴。
4)剪切带方向会受边界条件的限制。如应力的均匀性和位移以及砂粒粒径与试样尺寸等。
5)不同沉积角度砂样的剪切带角度变化很大,各向异性规律明显。当沉积面方向和大主应力方向一致时,剪切带角度与M-C理论值接近;当沉积面方向和大主应力方向夹角为56°~67°,剪切带倾角最小,此时沉积面和剪切带的方向接近,剪切带角度和Roscoe理论接近。
砂土剪切带的细观研究[2-4]表明其粒径、形状等对剪切带的厚度有很大影响,因此,结合细观特性研究剪切带形成机理更符合材料的物理性质。
4 分叉理论与传统理论的对比
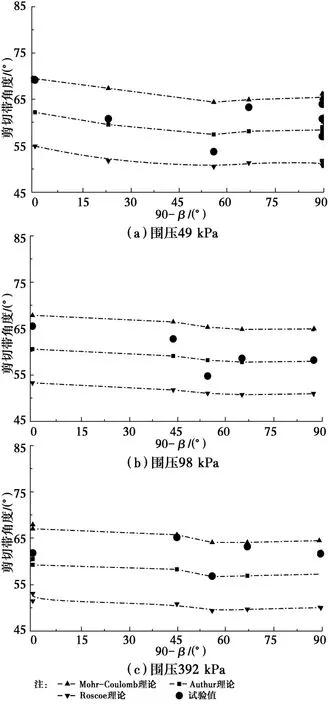
图5 破坏面与砂土沉积面试验值Fig.5 Test results between failure surface and sand deposition surface
图5为Tatsuoka等[8]通过试验观测到的剪切带角度的平面应变结果。试验做了49、98和392 k Pa三种围压、不同沉积角度试验。为了能够较好观测剪切带,饱和试样的表面都做了润滑处理,在中主应力加载面上采用激光斑纹法观测剪切带的形成过程。
试验结果给出了剪切带角度、内摩擦角和剪胀角的试验检测值,将该试验结果按照前面介绍的3种传统理论整理,即 M-C理论、Roscoe理论和Arthur理论。图5为剪切带观测的试验数据按传统3种理论整理的结果。图中可以看出,同种砂在相同的实验条件下,剪切带倾角试验值不唯一,不同沉积角度的砂样剪切带角度变化很大,表现出很强的各向异性。当沉积面方向和大主应力方向一致时,剪切带方向和最大应力等倾面方向(M-C理论)接近;当沉积面方向和小主应力方向夹角为56°~67°,剪切带倾角最小,接近于Roscoe理论值;3组围压下剪切带倾角变化趋势都相似,整体上随剪切带角度围压升高而略有降低,试验得到的3种理论的计算值都无法描述其表现的各向异性;图5从试验角度证实了传统的3种理论都无法较好解释剪切带倾角的各向异性规律。
Toyoura砂的剪切带倾角试验值和传统的3种理论的对比仍然得到了:M-C理论是试验上限值,Roscoe理论是试验的下限值,取上、下限的简单平均值的Arthur理论,尽管较前两种理论有所改善,然而,对其表现很强的各向异性还是很难解释。因此,本文用分叉理论进行预测。
图6为分叉理论预测与剪切带倾角的试验值的对比。分叉理论采用的模型详见文献[15]。从图6可以看出:同一孔隙比和同一围压条件下,分叉理论能够较好描述剪切带角度随沉积面角度的变化规律;3种围压下比较,整体上剪切带角度随围压的增大而减小;综合可以看出分叉理论对其表现的各向异性的变化趋势有较好的描述效果,但是预测值略低于试验结果,尤其在图6(c)中,392 kPa围压下比较明显,文献[15]对本构模型做了修正后有效解决了这个问题。
5 平面应变强度与三轴强度对比分析
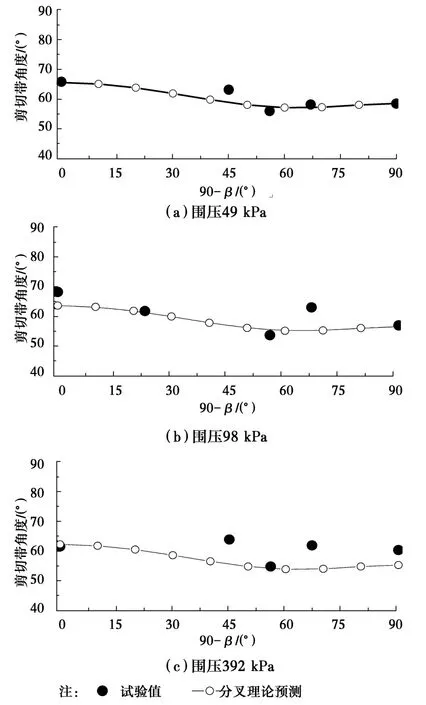
图6 分叉理论预测切带角度Fig.6 The angle simulations of shear band with bifurcation theory
图7为同一围压、同一孔隙比、不同沉积面角度的平面应变试验和三轴试验值与模拟值。平面应变试验为Tatsuoka等[8]的研究成果,三轴试验为Oda等[9]和Lam 等[19]不同试样尺寸的试验结果,试验的围压均为98 k Pa,孔隙比控制接近。为了能够直观反映平面应变试验强度和三轴试验强度值的关系,图7做了归一化,归一化强度为φf/φ(β=90°)。从图7可以看出平面应变试验和三轴压缩试验的规律差别很大,三轴压缩强度随沉积面角度是单调变化的,然而平面应变试验则是在大主应力轴与沉积平面夹角为56°~64°时强度达到最小值,然后随沉积面角度的增大强度又有一定增加;另外,图7中的试验可以看出,平面应变和三轴压缩强度的关系并不是像一般土力学中关于土的抗剪强度形成的概念,即:在相同条件下平面应变强度总是比三轴压缩强度高20%左右,而是在大主应力轴与沉积平面夹角为56°~64°时,平面应变强度可能接近三轴压缩强度。因此,就会产生这样的疑问:相同的砂、相同的制样方法和相同应力条件,两者的强度规律差异为什么如此明显?
强度差异的根本原因在于砂土的各向异性和是否有剪切带的产生。砂土为各向同性时,两者关系简单,都不随旋转角的变化而变化,三轴强度高于平面应变强度;砂土为各向异性时,两者都随旋转角的变化而变化。三轴试验强度单调增加,平面应变强度则是先减小然后增大。两者相比,三轴压缩试验很难观察到剪切带的形成,然而平面应变试验都观测到了明显的剪切带,因此,平面应变状态下必须考虑剪切带对强度的影响。剪切带形成的内在机理还需要结合砂土的细观分析才能够较好解释。
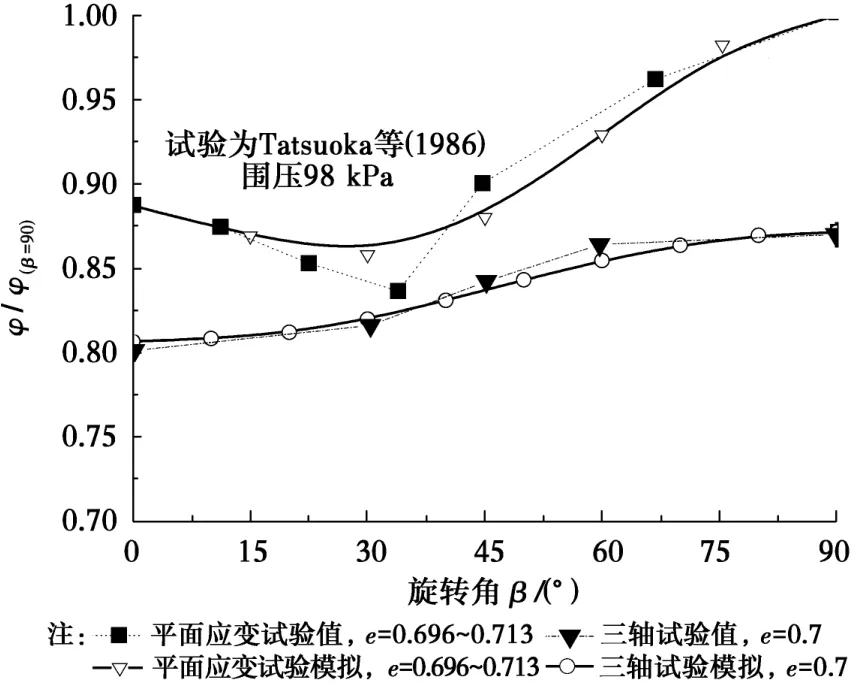
图7 Toyoura砂的各向异性强度规律(文献[9])Fig.7 Anisotropy strength of Toyoura sand
6 平面应变各向异性强度的细观解释
砂土的各向异性强度受砂土细观特性和组构方向的影响。图8是剪切带方向相对沉积面方向的两种关系。Tatsuoka等[8]试验发现:当大主应力相对沉积面为56°和67°时,只得到了图8(b)型剪切带,当旋转角为23°和79°时,多数试验都表现出图8(a)型的剪切带,当沉积面角度为45°时,两种形式的剪切带都会出现。可见剪切带不一定沿沉积面方向,但是沉积面角和剪切带角接近时会诱发剪切带过早产生。
结合平面应变剪切带试验分析结果和沉积面与剪切带产生的关系可以解释平面应变强度的特性。当大主应力轴与沉积平面夹角为56°~65°时,此时剪切带和沉积面方向很接近,而且只得到了b型剪切带,因此,当沉积面角度和剪切带角度接近时,较早触发应变局部化产生,从而,土体表现了比较低的强度;当大主应力轴与沉积平面方向夹角为0°时,即沉积面和中主应力方向一致,沉积面方向受刚性约束,抑制了应变局部化的发生,因此,这种条件下强度达到最大值。
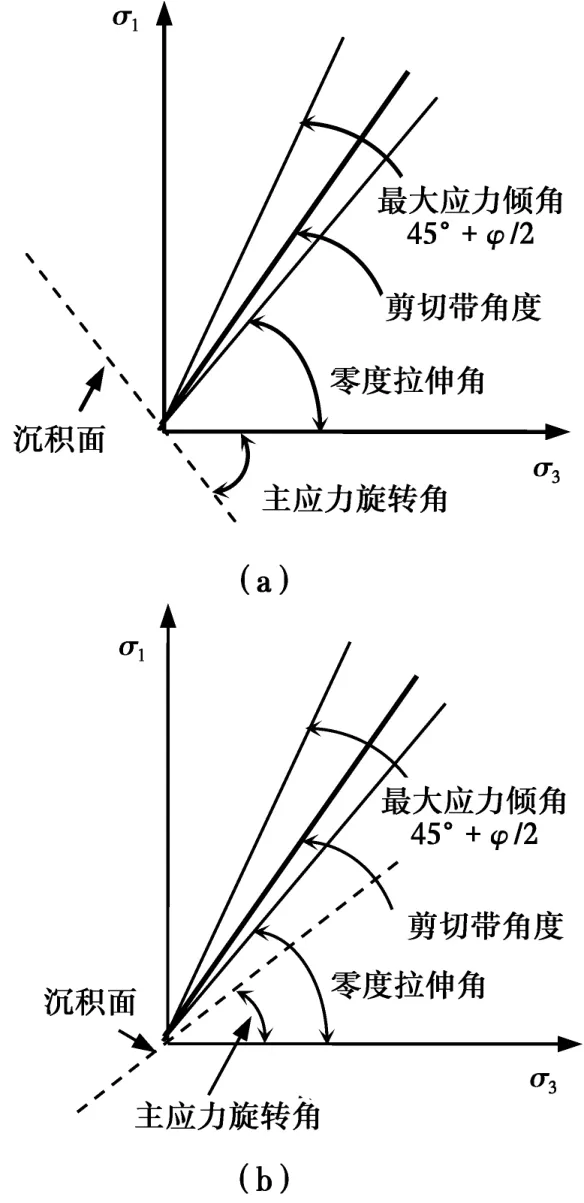
图8 砂土沉积面和破坏面的关系Fig.8.The relationship between sand bedding plane and failure surface
同时,细观研究发现平面应变状态和轴对称状态各向异性程度存在差异的主要原因是:砂土在平面应变状态下会表现更多的局部化变形,颗粒排列不易改变;然而,在轴对称条件下砂土会表现更多的均匀变形,这种条件下颗粒排列容易变化。因此,同种砂的平面应变强度各向异性比常规三轴试验强度表现的更明显。
综上所述,考虑砂土的细观组构影响时,模型能够较好反映三轴条件下主应力相对砂土沉积面不同角度的强度规律,结合分叉理论模型可以自然描述平面条件下剪切倾角受砂土细观沉积角度的影响,再次验证了宏细观结合本构模型描述砂土各向异性的合理性。
7 结 语
根据各向异性Toyoura砂的剪切带角度的试验结果,用传统三种理论预测的剪破度与分叉理论预测的结果进行了对比分析。
按照三种传统理论对试验数据整理后发现,各向异性砂土的三轴试验剪切带角度和平面应变条件下的剪切带角度表现出明显不同的各向异性,必须建立各向异性本构关系对其特性进行描述。然而,建立在三轴试验基础上的本构关系对该试验条件下的剪切带角度规律可以较好描述,但无法对平面应变条件下的剪切带角度规律进行描述。各向异性模型结合分叉理论则可以较好解决了这个问题。
对比分析结果表明,模型结合分叉理论能够描述多种应力状态下平面应变剪切带角度的变化规律。能够从细观角度解释平面应变条件下砂土沉积面对各向异性剪切带角度规律的影响。
[1]Roscoe K H.The influence of strains in soil mechanics[J].Geotechnique,1970,20(2):129-170.
[2]Nemat-Nasser S,Okada N.Strain localization in particulate media [C]// Proceedings of the 12th Engineering Mechanics Conference,1998,LA Jolla,CA.
[3]Alshibli K A,Sture L S.Sand shear band thickness measurements by digital imaging techniques [J].Journal Computing in Civil Engineering,ASCE,1999,13(2):103-109.
[4]Francesco T,Jack W,Edward A.Observing strain localisation processes in bio-cemented sand using x-ray imaging[J].Granular Matter,2011,13(3):247-250.
[5]Finno R J,Harris W W,Viggiani G.Shear bands in plane strain compression of loose sand [J].Geotechnique,1997,47(1):149-l65.
[6]Vardoulakis I,Goldscheider M,Gudehus G.Formation of shear bands in sand bodies as a bifurcation problem[J].International Journal for Numerical and Analytical Methods in Geomechanics,1978,2(2):99-128.
[7]Abelev A V,Lade P V.Effects of cross-anisotropy on three-dimensional behavior of sand I:Stress-strain behavior and shear banding[J].Journal of Engineering Mechanics,ASCE,2003,129(2):160-166.
[8]Tatsuoka F,Sakamoto M,Kawamura T,et al.Strength and deformation characteristics of sand in plane strain compression at extremely low pressures[J].Soils and Foundations,1986,26(1):65-84.
[9]Oda M.Experimental study of anisotropic shear strength of sand by plane strain tests [J].Soils and Foundations,1978,18(1):25-38.
[10]Yoshida T,Tatsuoka F.Deformation property of shear band in sand subjected to plane strain compression and its relation to particle characteristics [C]//Proc.14th ICSMFE,Hamburg,1997,l(1):237-240.
[11]陈立平,张顶立,房倩,等.基于细观统计的各向异性砂土摩擦特性与破坏机制研究[J].岩石力学与工程学报,2015,33(Supl):3291-3298.
Chen L P,Zhang D L,Fang Q,et al.Research on friction characteristics and failure mechanism of anisotropic sand based on micro-statistics[J].Chinese Journal of Rock Mechanics and Engineering,2015,33(Supl):3291-3298.(in Chinese)
[12]宋飞,张建民.考虑侧向变形的各向异性砂土土压力试验研 究 [J].岩 石 力 学 与 工 程 学 报,2009,28(9):1884-1895.
Song F,Zhang J M.Experimental study of earth pressure for anisotropic sand considering lateral displacement[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(9):1884-1895.(in Chinese)
[13]李学丰,黄茂松,钱建固.宏细观结合的砂土各向异性破坏准则[J].岩石力学与工程学报,2010,29(9):1885-1892.
Li X F,Huang M S,Qian J G.Failure criterion of anisotropic sand with the method of macro-micro incorporation[J].Chinese Journal of Rock Mechanics and Engineering,2010,29 (9):1885-1892. (in Chinese).
[14]李学丰,黄茂松,钱建固.宏细观结合砂土单剪试验的非共轴模拟[J].岩土力学,2013,34(12):3417-3424.
Li X F,Huang M S,Qian J G.Analysis of non-coaxial characters of sand for simple shear test with the method of macro-meso-incorporation [J].Rock and Soil Mechanics,2013,34(12):3417-3424.(in Chinese)
[15]李学丰,黄茂松,钱建固.基于非共轴理论各向异性砂的应 变 局 部 化 分 析 [J].工 程 力 学,2014,31(3):205-211.
Li X F,Huang M S,Qian J G.Strain localization analysis of anisotropic sands based on non-coaxial theory[J].Engineering Mechanics,2014,31(3):205-211.(in Chinese)
[16]Valanis K C.Banding and stability in plastic materials[J].Acta Mechanica,1989,79:113-141.
[17]钱建固,黄茂松.土体应变局部化的理论解析[J].岩土力学,2005,26(3):432-437.
Qian J G,Huang M S.An analytical solution for criterion of onset of strain localization of soils[J].Rock and soil Mechanics,26(3):432-437.(in Chinese)
[18]Arthur J F R,Dunstan T,Al-Ani Q A J,et al.Plastic deformation and failure in granular media [J].Geotechnique,1977,27(1):53-57.
[19]Lam W K,Tatsuoka M,Chen L P,et al.Initial anisotropic fabric andσ2on strength and deformation characteristics of sand [J].Soils and Foundations,1988,28(1):89-106.
(编辑 王秀玲)
2015-02-28
National Natural Sciencal Foundation of China(No.5168050,61463043);Ningxia Natural Sciencal Foundation of Key Projects(No.NZ13001);Science and Technology Support Project in Ningxia(In2013).
Author brief:Li Xuefeng(1976-),Ph D,associate professor,main interests:geotechnical engineering and the constitutive model,(E-mail)lixuefeng1928@163.com.
Theoretical analysis of shear band angle for anisotropy sand
Li Xuefeng,Yuan Qi,Ma Wenguo
(Solid Mechanics Institute,Ningxia University,Yinchuan 750021,P.R.China)
Aiming at the test results of shear band angle under plane strain conditions for anisotropy sand,a comparative analysis was carried out based on the three traditional theories and bifurcation theory.The results of shear band under plane strain condition described by the three traditional theories showed the traditional theories could estimate the minimum,middle and maximum values of the shear band angle of sand,whilst it could not t explain the anisotropy behaviors of shear band.The shear band under the plane strain conditions was easily observed,and it induced shear bands that reduced material strength when the directions of shear band and sand deposition were the same.It resulted in the different anisotropy characteristics in the conventional triaxial conditions and plane strain conditions.Such different characteristics could be explained using bifurcation theory together with anisotropy model.With the direction variation of sand deposition,the model ccould explain the monotonic behaviors of shear angled under conventional triaxial condition from microscopic viewpoint,the bifurcation theory combined with the model could describe the behavior of shear angled under plane strain condition which decreased first and then increased.The comparative analysis of four theories showed that bifurcation theory together with anisotropic model well explained the different shear properties between plane strain and conventional triaxial under various stress conditions,and one could well explain it from the microscopic viewpoint.
shear band;bifurcation theory;anisotropy;plane strain;meso feature
TU443
A
1674-4764(2015)04-0090-07
10.11835/j.issn.1674-4764.2015.04.012
2015-02-28
国家自然科学基金(5168050、61463043);宁夏自然科学基金重点项目(NZ13001);宁夏科技支撑计划(2013年)
李学丰(1976-),男,博士,副教授,主要从事岩土工程及本构模型的研究,(E-mail)lixuefeng1928@163.com。

