一类变时滞的不同复杂网络的线性广义同步

巩长忠，李飞燕

（中国民航大学理学院，天津 300300）

一类变时滞的不同复杂网络的线性广义同步

巩长忠，李飞燕

（中国民航大学理学院，天津 300300）

讨论了一类变时滞的不同复杂网络间的线性广义同步问题。基于Lyapunov稳定性理论和自适应控制方法，得到了网络线性广义同步的充分条件。此外，每个网络中的节点和耦合项均含有时滞函数，且网络的维数不同、拓扑结构不恒等，每个网络节点的动力学也可以不同。最后数值模拟结果证实了该方法的合理性，并验证了同步速度受自适应律强度的影响。

不同复杂网络；线性广义同步；变时滞；自适应控制器

在过去的10年中，对复杂网络的研究已渗入到很多科学领域，如在物理学、生物医学、工程学和社会学都有着十分广泛的应用[1-3]。复杂网络是节点间相互作用的大集合，在这个集合中，每个节点是含有具体信息的基本单元。复杂网络的例子在自然界中普遍存在，包括因特网、万维网（WWW）、神经网络、生态网络、新陈代谢网和人际关系网等。复杂网络的本质就是其复杂性，包括网络的拓扑结构、动力学演化、节点多样性等，这引起了许多学者对复杂网络的关注，特别是网络的同步。网络同步是一个重要且有趣的现象，已成为复杂网络研究的一个焦点。到目前为止，许多同步的定义先后被学者提出，如完全同步[4]、滞后同步[5]、广义同步[6]、投影同步[7]等。与此同时，也提出了许多复杂网络同步的控制方法，如牵制控制[8]、反馈控制[9]、自适应控制[10]、脉冲控制[11]等。然而许多研究仅仅关注在单个网络内节点间的同步，即内部同步[12]。与之不同的是外部同步，指的是两个或多个复杂网络间的同步，这在现实世界中随处可见，如艾滋病，禽流感和H1N1流感起初都是通过两个网络进行传播的。

众所周知，目前已有很多关于两个复杂网络同步的研究，但很少考虑时滞[13]或仅仅考虑了耦合时滞[10]，研究节点带变时滞的就更少了。实际上，许多网络的同步现象不仅受耦合时延影响而且也受节点时延的影响，如流行病毒的扩散以及网络的拥塞现象，还有物理网络、生物环境网络和经常接触的医学网络，都受到了时延的影响。大多数时滞都是时变的，即系统的演变除了与系统当前的状态相关，还跟过去某个时刻的状态相关。先前的很多文献仅仅对节点和耦合项均含时滞的单个网络的内部同步进行了研究[14]，而对于外部同步，研究节点和耦合项都含时滞函数的不同复杂网络同步是少之又少。因此，研究节点和耦合项都含变时滞的不同复杂网络间的线性广义同步是很有现实意义的。

本文首先介绍了两个完全不同的复杂网络模型，在模型中节点和耦合项都含有不同的时滞函数，然后基于Lyapunoy稳定性理论，通过设计合适的自适应控制器，获得了网络同步的充分条件，在广义同步意义下响应网络在控制器作用下渐近同步于驱动网络。这种方法适用于几乎所有时滞复杂网络。最后数值结果证实了方法的有效性。

1 模型描述

考虑一类含有N个非恒等节点，且节点和耦合项均含不同时滞函数的复杂网络，其形式如下

其中：xi（t）=（xi1，xi2，…，xin）T∈Rn代表第i个节点的状态；fi（·）：Rn→Rn是可微的非线性连续函数；τ1（t）与τ2（t）为时滞函数；A∈Rn×n是内部耦合矩阵；C=（cij）N×N∈RN×N是配置矩阵。矩阵C定义如下：若第i个节点与第j个节点之间有关联（i≠j），则cij≠0，反之cij=0，并且即C中每一行元素和为0，记方程（1）为驱动网络。

把含有非线性控制器的时滞网络记为响应网络，其形式如下

其中：yi（t）=（yi1，yi2，…，yim）T∈Rm代表第i个节点的状态；gi（·）：Rm→Rm是可微的非线性连续函数；ui（t）∈Rm是控制器；B∈Rm×m是内部耦合矩阵；D=（dij）N×N∈RN×N是配置矩阵，与矩阵C定义相同（C≠D）。即方程（2）与方程（1）具有不同的网络拓扑结构，但有相同的节点数目。

定义1 对于线性函数φ：Rn→Rm，如果驱动网络（1）中的xi（t）和响应网络（2）中的yi（t）满足

则网络（1）、网络（2）达到 LGS（linear generalized synchronization），即线性广义同步。其中φ（xi（t））= Pxi（t）+Q，P、Q都为常数矩阵且P∈Rm×n，Q∈Rm。

引理1 任给x，y∈Rn以及正定矩阵S，有[15]

引理2 对于非线性连续函数 fi（xi（t），xi（tτ1（t））），假设存在常数α1≥0、α2≥0使得fi满足semi-Lipschitz条件，则有[15]

其中：xi（t），yi（t）∈Rn，xi≠yi并且t≥0（i=1，2，…，N），即式（5）为向量不等式。

假设1 假设时滞函数τ1（t）、τ2（t）（＞0）是可微的（η1、η2为常数），并满足以下条件[15]

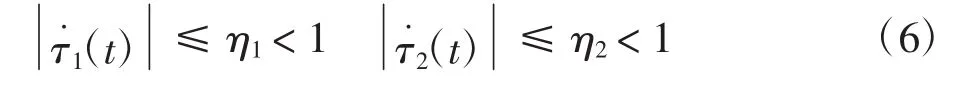
2 同步理论分析

定理1 若假设1与下列3个条件同时成立：①响应系统（2）是全状态可测的；适应同步控制器ui（t）满足如下形式，则驱动系统（1）与响应系统（2）将达到线性广义同步LGS，即

其中：λ、β是大于0的常数，用来调节同步误差的振幅和同步误差的收敛速度。

证明定义网络（1）和网络（2）的同步误差为

设

构造李雅普诺夫函数为

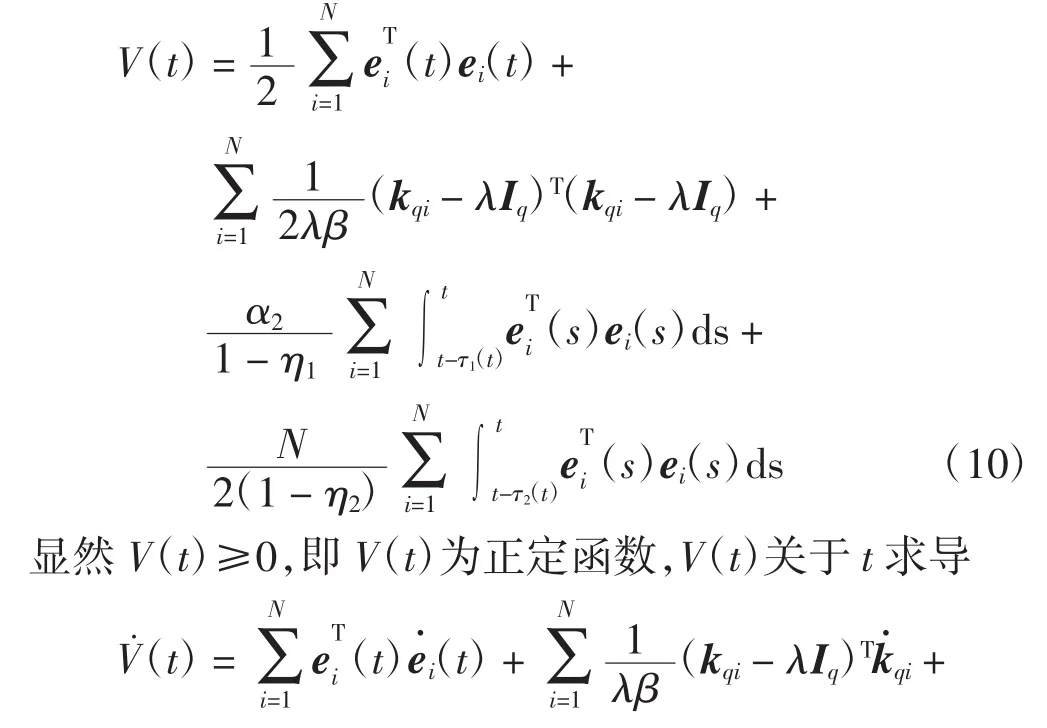
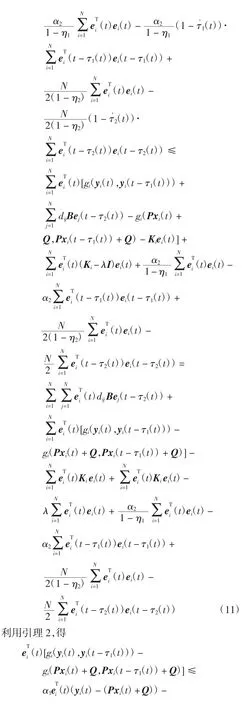
从而S是一个负定矩阵，即V˙（t）＜0。由Lyapunoy稳定性定理可得

由此可知误差ei（t）的0解是渐近稳定的，故节点和耦合项均含时滞函数的两个完全不同的复杂网络（1）和网络（2）在控制器（7）的作用下实现了LGS。

注1 本文中耦合配置矩阵C和D不必是对称或可约矩阵，对于内部耦合矩阵A和B也没任何约束条件，网络的每个节点可以代表不同的动力学。最后，节点时滞函数τ1（t）和耦合时滞函数τ2（t）可以不同，因此以上介绍的方法适用于几乎所有的时滞复杂动力学网络。

注2 自适应律强度λ可以提前选择来调整同步速率，理论上λ值越大，同步速度就越快，然而对同步而言不等式λ＞λ*仅仅是一个充分条件而非必要条件，即当λ＜λ*时，网络（1）和网络（2）也可以达到线性广义同步。

3 数值仿真

为了证实上述方法的可行性，将在Matlab环境下进行数值仿真。为了便于仿真，研究由10个节点组成的复杂网络，分别选取三维和四维的系统，描述如下

其中：xi1、xi2、xi3为第i个系统的状态变量（i=1，2，…，10）；τ1（t）为节点的时滞函数。

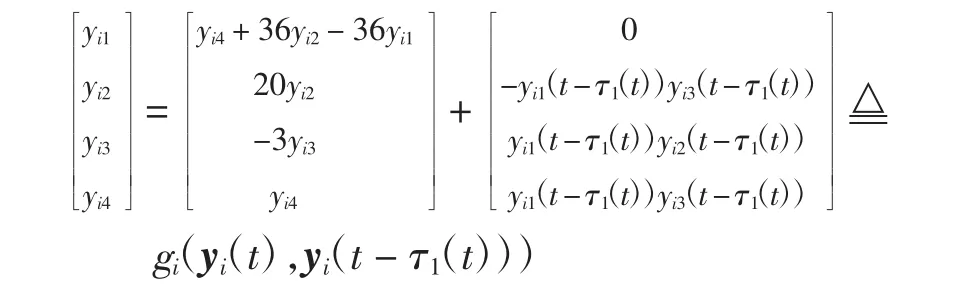
其中：yi1、yi2、yi3、yi4为第i个系统的状态变量；τ1（t）为节点的时滞函数。

由于网络的配置矩阵是任意的，所以不妨取网络的配置矩阵C和D为

取内部耦合矩阵为恒等矩阵，即A∈I3×3，B∈I4×4，为简单起见，取时滞函数τ1（t）=τ2（t）=0.1-0.02cos 2t，由于故取η=0.05，则整个复杂网络为

在数值模拟实验中，取式（16）作为驱动网络，式（17）作为响应网络。取α1=α2=1，则

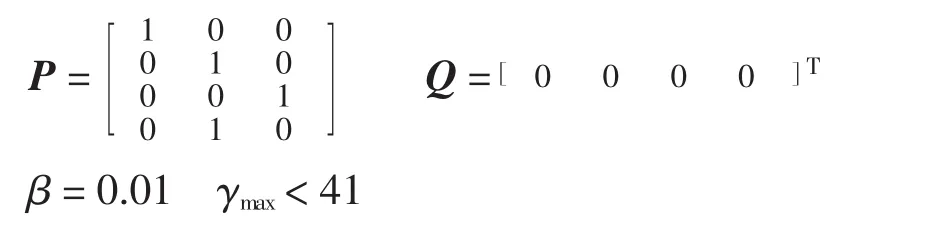
由式（15）可知

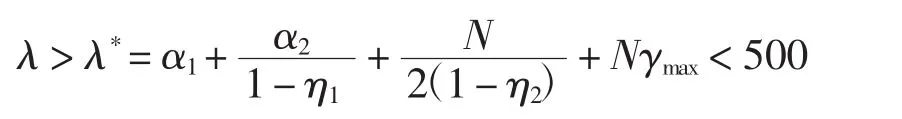
故取λ=500。驱动响应网络的初值在（0，1）之间任意取。在Matlab环境下进行模拟试验，利用定理1中的控制器如图1所示，可以看到同步误差曲线ei1、ei2、ei3与ei4随着时间的推移都趋于0。

图1 λ=500时系统的同步误差曲线Fig.1 Synchronization error curves with λ=500

若令λ=600，其它值不变，在Matlab环境下进行模拟试验，利用定理1中的控制器如图2所示，可以看到同步误差曲线ei1、ei2、ei3与ei4随着时间的推移都趋于0。比较图1与图2的误差曲线，可以看出图2比图1同步的速度要快，从而可得λ值越大，同步速度就越快。

图2 λ=600时系统的同步误差曲线Fig.2 Synchronization error curves with λ=600

令λ=100，其它值不变，利用定理1中的控制器在Matlab环境下进行仿真，结果如图3所示，可以看出同步误差曲线ei1、ei2、ei3与ei4也可以趋于0，即驱动响应网络在λ＜λ*时也可以趋于同步，同步速度较图1、图2慢，从而可验证λ＞λ*仅仅是网络同步的一个充分而非必要条件。

图3 λ=100时系统的同步误差曲线Fig.3 Synchronization error curves with λ=100

4 结语

在实际应用中，节点和耦合项均含时滞的不同复杂网络是不可避免的，而这在以往的研究中常常被忽略。本文采用自适应控制的方法考虑了节点和耦合项均带时滞函数的两个不同的复杂网络间的线性广义同步。每个网络的节点不恒等且网络维数及拓扑结构也不同，最后数值仿真证实了方法的有效性，并对同步的快慢进行了验证，发现同步速度受自适应强度λ影响，λ越大同步越快。

现有与此类似的研究主要有如下两个方面的工作：①节点和耦合项均含时滞函数的复杂网络模型，此模型仅针对内部同步而言；②两个不同复杂网络的耦合项含变时滞，而节点不含时滞的自适应外部同步模型。本文模型对耦合项含时滞而节点不含时滞的外部同步情况进行推广，具有更广的适用范围。

[1]DAI Y，CAI Y Z，XU X M.Synchronization criteria for complex dynamical networks with neutral-type coupling delay[J].Physica A，2008，387：4673-4682.

[2]吕金虎.复杂网络的同步理论、方法、应用与展望[J].力学进展，2008，38（6）：713-722.

[3]LIU Y Z，JIANG C S，LIN C S，et al.Chaotic synchronization secure communications based on the lorenz systems switch[J].Journal of Electronics＆Information Technology，2009，29（11）：2641-2644.

[4]AGIZA H N.Chaos synchronization of Lü dynamical system[J].Nonlinear Analysis，2004，58（1/2）：11-20.

[5]LI C D，LIAO X F，WONG K W.Chaotic lag synchronization of coupled time-delayed systems and its applications in secure communication[J].PhysicaD：NonlinearPhenomen，2004，194（3/4）：187-202.

[6]RULKOV N F，SUSHCHIK M M，TSIMRING L S，et al.Gneralized synchronization of chaos in directionally coupled chaotic systems[J]. Phys Rev E，1995，51：980-994.

[7]LI G H.Modified projective synchronization of chaotic system[J].Chaos Solitons and Fractals，2007，32（5）：1786-1790.

[8]WANG S G，Yao H X.Pinning synchronization of time-varying delay coupledcomplexnetworkswithtime-varyingdelayeddynamicalnodes[J]. Chin Phys B，2012，21（5）：119-125.

[9]WU X J，LU H.Generalized function projective（lag，anticipated and complete）synchronization between two different complex networks with nonidentical nodes[J]//Commun Nonlinear Sci Numer Simulat，2012，17（7）：3005-3021.

[10]ZHENG S，WANG S G，DONG G G，et al.Adaptive synchronization of two nonlinearly coupled complex dynamical networks with delayed coupling[J].Commun Nonlinear Sci Numer Simulat，2012，17：284-291.

[11]LI K，LAI C H.Adaptive-impulsive synchronization of uncertain complex dynamical networks[J].Phys Lett A，2008，372：1601-1606.

[12]罗 群，吴 薇，李丽香，等.节点含时滞的不确定复杂网络的自适应同步研究[J].物理学报，2008，57（3）：1529-1533.

[13]DAI H，JIA L X，ZHANG Y B.Adaptive generalized matrix projective lag synchronization between two different complex networks with nonidentical nodes and different dimensions[J].Chin Phys B，2012，21（12）：141-152.

[14]李红敏，褚衍东，张建刚，等.带有时变时滞和线性耦合的复杂网络同步[J].昆明理工大学学报，2011，36（2）：50-55.

[15]WANG S G，YAO H X.Pinning synchronization of time-varying delay coupledcomplexnetworkswithtime-varyingdelayeddynamicalnodes[J]. Chin Phys B，2012，21（5）：1-7.

（责任编辑：杨媛媛）

Generalized linear synchronization of different complex networks with time-varying delays

GONG Chang-zhong，LI Fei-yan
（College of Science，CAUC，Tianjin 300300，China）

Generalized linear synchronization of different complex networks with time-varying delays is introduced.Based on Lyapunov stability theory，some generalized linear synchronization sufficient conditions are derived by adaptive control method.Furthermore，each network with time-varying coupling delays and time-varying delays in dynamical nodes may have different dimensions and its topological structure is also nonidentical.Nodes in either network may have identical or different dynamics.A numerical simulation example is also provided to testify the rationality of the current method，demonstrating that the synchronization rate is affected by adaptive law strength.

different complex networks；generalized linear synchronization；time-varying delays；adaptive controller

TP273

：A

：1674－5590（2015）06－0055－06

2014-07-04；

：2014-09-19

：中央高校基本科研业务费专项（ZXH2012K002，3122014K008）；天津市自然科学基金青年项目（13JCQNJC04400）；中国民航大学科研启动基金项目（2012QD10X）

巩长忠（1959—），男，山东蓬莱人，教授，博士，研究方向为非线性控制.