液化场地桥梁足尺桩抗震简化分析方法①

张效禹， 唐　亮,3， 凌贤长， 李　惠

(1. 哈尔滨工业大学土木工程学院，黑龙江 哈尔滨 150090；

2. 结构工程灾变与控制教育部重点实验室 哈尔滨工业大学，黑龙江 哈尔滨 150090；

3.地质灾害防治与地质环境保护国家重点实验室 成都理工大学，四川 成都 610059)



液化场地桥梁足尺桩抗震简化分析方法①

张效禹1,2， 唐亮1,2,3， 凌贤长1,2， 李惠1，2

(1. 哈尔滨工业大学土木工程学院，黑龙江 哈尔滨 150090；

2. 结构工程灾变与控制教育部重点实验室 哈尔滨工业大学，黑龙江 哈尔滨 150090；

3.地质灾害防治与地质环境保护国家重点实验室 成都理工大学，四川 成都 610059)

摘要：采用国际VELACS项目中离心机试验标定的内华达砂的动力计算参数，建立液化场地足尺桩-土动力相互作用分析的三维有限元模型；获得不同幅值的正弦波作用下桩-土动力相互作用的p-y曲线，修正并发展一种可用于液化场地桩-土动力相互作用分析的宏单元模型，并基于非线性文克尔地基梁模型建立桥梁足尺桩抗震分析的数值模型与简化方法，通过有限元分析结果验证该简化方法的正确性。

关键词：宏单元模型； 简化方法； 足尺桩-土动力相互作用； 非线性有限元分析； 液化场地

0引言

强震作用下场地桩-土相互作用的分析是进行液化场地桥梁桩基结构抗震分析的基本依据。虽然模型试验(离心机试验和振动台试验)能够有效地进行桩-土动力相互作用分析，但存在耗时长、费钱且考虑的影响因素有限等不足。目前数值方法已成为桥梁桩基抗震设计的重要手段之一，它可以避免试验方法的诸多缺点，并且较好地模拟地震下桩的动力特性。然而数值方法也具有建模途径较复杂、计算参数不易选取且计算机时较长等缺点，在实际工程应用中受到很大限制[1-2]。因此发展一种高效且可靠的液化场地桥梁桩基抗震分析方法，即动力特性的分析方法，具有重要意义。

非线性文克尔地基梁法作为一种简化方法，可以很好地模拟地震下土体的强非线性、辐射阻尼及桩-土界面处分离和滑动等特性，已在工程实践中得到广泛应用。然而将非线性文克尔地基梁法应用到液化场地桩基抗震分析中的研究尚不成熟，现有研究工作更多是通过一维自由场地分析获得砂层孔压比衰减修正，得到弹簧刚度，如Kagawa等[3]、Liyanapathirana等[4]及Sarkar等[5]基于文克尔地基梁模型建立的液化场地桥梁桩基抗震分析的简化方法。

地震作用下桩-土动力相互作用是一个极其复杂的过程，对桩-土动力相互作用实施精细化模拟的关键在于如何准确刻画其动力特性。通常将土体按距离桩的远近分为近场土体、远场土体和自由场土体。地震作用下近场土体表现出明显的非线性特性，且在强地震作用下桩和土体之间还可能出现裂缝及桩土相对滑动的现象。远场土体距离桩较远，受到桩的作用较小，土体表现出近似弹性的行为，对远场土体模拟的关键在于描述其辐射阻尼效应。自由场土体几乎不受桩的影响，但其滤波作用会使桩受到不同的激励作用。目前国内外学者提出了多种宏单元模型：如Matlock模型[6]、Naggar模型[7]及Boulanger模型[8]等，试图准确表述模拟地震作用下桩-土相互作用的动力特性。其中Boulanger提出的宏单元模型由弹性单元、塑性单元和裂缝单元串联组成，能够更全面且合理地模拟桩-土相互作用的物理过程。目前液化场地桩基的抗震研究工作多集中于小比例模型试验及相应的理论分析。本文拟通过修正并发展Boulanger模型，提出一种可进行液化场地桥梁足尺桩-土动力相互作用分析的简化方法。

1液化场地桥梁足尺桩-土动力相互作用数值模拟与分析

采用唐亮等[9-12]提出的液化场地桩-土动力相互作用分析的基本数值建模途径与计算方法，采用国际VELACS(Verification of liquefaction analysis using centrifuge studies)项目标定的相对密度40%的Nevada(内华达)砂计算参数，建立液化场地桥梁足尺桩基地震反应分析三维有限元模型(图1)。内华达砂的计算参数见表1[11-12]。

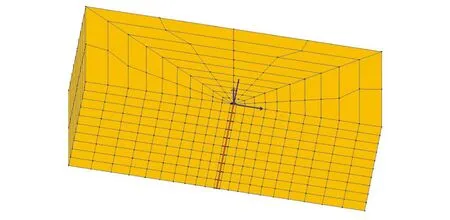
图1　有限元模型Fig.1　Finite element model

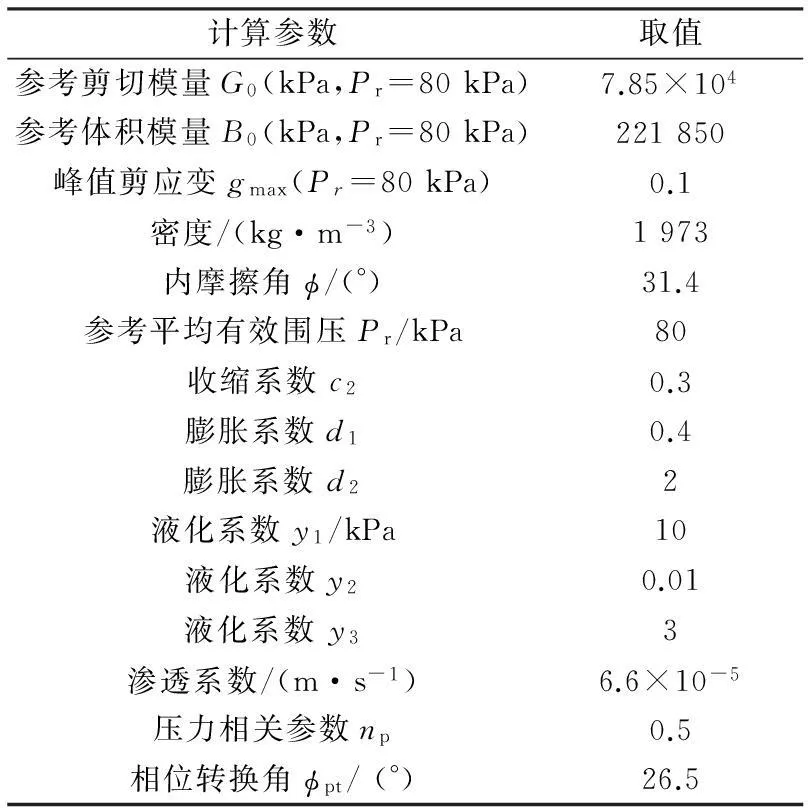
计算参数取值参考剪切模量G0(kPa,Pr=80kPa)7.85×104参考体积模量B0(kPa,Pr=80kPa)221850峰值剪应变gmax(Pr=80kPa)0.1密度/(kg·m-3)1973内摩擦角ϕ/(°)31.4参考平均有效围压Pr/kPa80收缩系数c20.3膨胀系数d10.4膨胀系数d22液化系数y1/kPa10液化系数y20.01液化系数y33渗透系数/(m·s-1)6.6×10-5压力相关参数np0.5相位转换角ϕpt/(°)26.5

模型中，桩径0.6 m，桩长12 m，弹性模量E=3.0×107kPa，桩顶施加240 kg重的质量点以模拟上部结构在地震中的惯性效应。桩采用线弹性梁-柱单元模拟，土层为10 m厚的饱和内华达砂，水位线位于地表处。模型长30.6 m×宽15 m×高10 m。桩与土采用刚性连接杆模拟。砂土选用的本构模型、边界条件和计算收敛准则等其他建模的技术细节详见文献[9-10]。

2动力p-y曲线

2.1不同加载幅值下的动力p-y曲线

采用上述有限元模型，模型基底输入不同幅值的1 Hz正弦波，获得液化场地桩-土动力相互作用的p-y曲线，其中p为桩和土之间的相互作用力(简称“土反力”)，y为桩和土之间的相对位移。图2为不同幅值(0.05g、0.10g、0.15g和0.25g)的1 Hz正弦波输入下埋深4 m处桩与土相互作用的动力p-y曲线。图3为不同幅值的正弦波下埋深6 m处砂层超孔压时程。

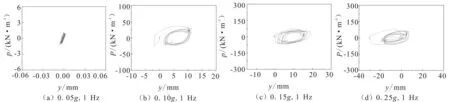
图2　加载幅值对埋深4 m处土体动力p-y曲线的影响Fig.2　Effect of loading amplitudes on dynamic p-y curves at the depth of 4 m

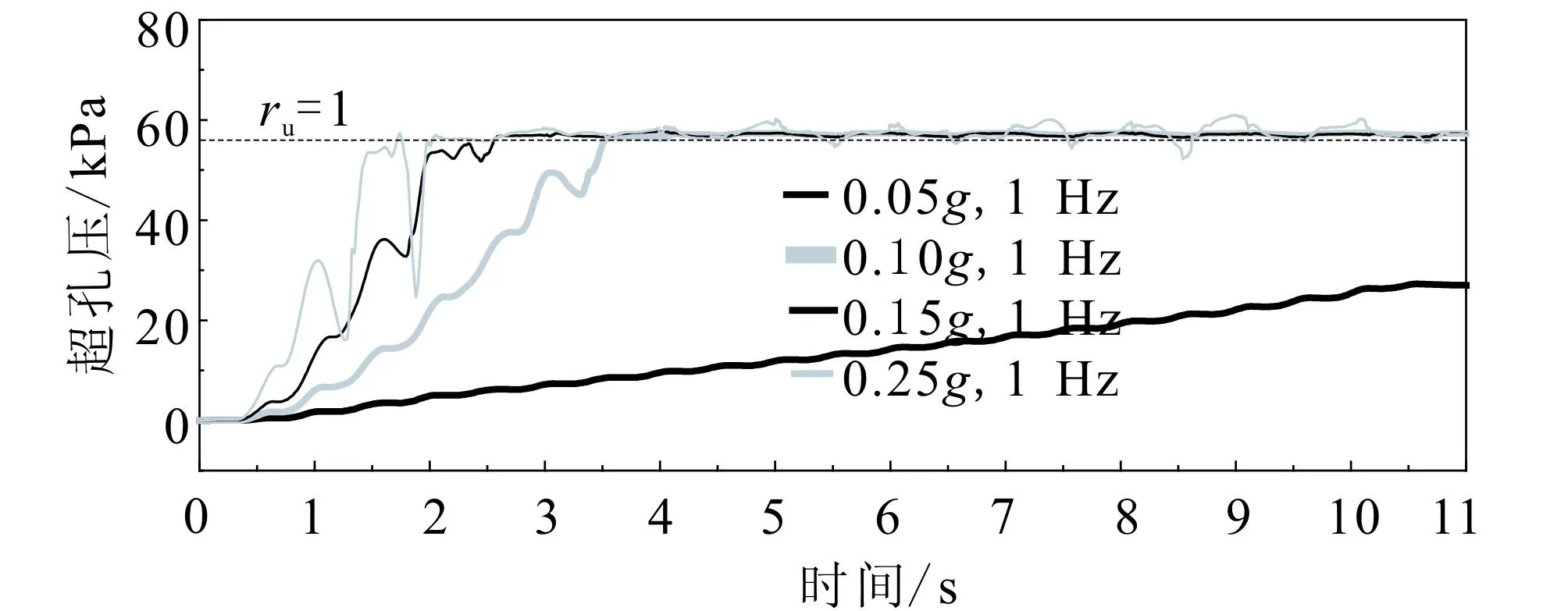
图3　加载幅值对埋深6 m处砂层超孔压时程影响Fig.3　Effect of loading amplitudes on excess pore pressure　　　 time-histories of sand at the depth of 6 m

由图2、图3可知，加载幅值较小时(0.05g)，土体的超孔压较小，p-y曲线滞回圈几乎呈线性；随着加载幅值的增加，土体发生液化(孔压比ru=1)，滞回圈面积逐渐越大；当幅值由0.15g增至0.25g时滞回圈面积并未发生明显增大，这应该主要是由于土反力p接近极限土反力pult所致。此外，随着加载幅值的增加，土体超孔压增长率逐渐变大。

2.2动力p-y曲线的骨干曲线

借鉴唐亮[1]提出的方法，引入构造土的动应力-动应变关系曲线骨干线的基本思想，将不同加载幅值下的动力p-y曲线顶点拟合得到其骨干曲线，据此发展液化场地桩-土动力相互作用分析的简化方法。由上述可知，土体孔压比对动力p-y曲线影响显著，土体单位桩长的极限承载力pult在土体受到震动过程中随孔压比的变化而改变。因此需要构建不同孔压比下动力p-y曲线的骨干曲线。将孔压比按每0.2一级划分六段：0～0.2、0.2～0.4、0.4～0.6、0.6～0.8、0.8～1.0和1.0。

动力p-y曲线的骨干曲线构建过程为：

(1) 孔压比ru=1.0

根据上述研究可知，孔压比ru=1.0时动力p-y曲线滞回圈表现出明显的滞后性和变形累积等特性，滞回圈顶点的位置很难确定。因此选取p-y曲线滞回圈每个加载周期的最大土反力pmax和最大桩土相对位移ymax点作为其顶点，以0.10g 1Hz正弦波输入下埋深4m处土体p-y曲线为例(图4)，选取点(p1，y1)、点(p2，y2)作为动力p-y曲线滞回圈顶点。将美国石油工程协会(AmericanPetraleumInstitute，API)规范[13]中推荐的标准砂土p-y曲线进行折减，拟合埋深4m处的骨干曲线[图5(a)]。折减系数Cz=0.16时，得到的曲线与滞回圈顶点的排列形式吻合较好，即埋深4m处土体的动力p-y曲线的骨干曲线为：

(1)

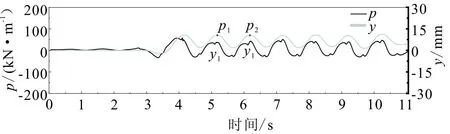
图4　0.10g 1 Hz正弦波输入下埋深4 m处　　　土体动力p-y曲线时程Fig.4　Dynamic p-y time history at the depth of 4 m under　　　 the input of sine wave with amplitude of 0.1g and　　　 frequency of 1 Hz

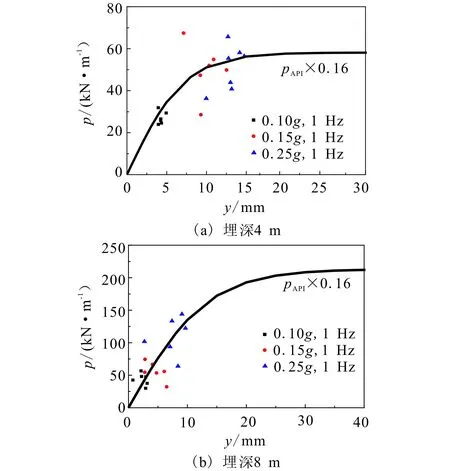
图5　埋深4 m和8 m处土体动力p-y曲线的　　　骨干曲线(ru=1.0)Fig.5　Backbone curve of the dynamic p-y curve at　　　 the depth of 4 m and 8 m (ru=1.0)

随后选取埋深8 m处土体的p-y曲线，验证折减系数Cz=1.6是否适用于其他埋深处的骨干曲线[图5(b)]。由图5(b)可以看出，虽然土反力p没有达到极限土反力pult，但是折减得到的骨干曲线初始部分与滞回圈顶点的排列形式吻合较好，因此可假定折减系数Cz=0.16同样适用于埋深8 m处土体。限于篇幅，不再对其他埋深处逐个进行检验(详见参考文献[2])。因此孔压比ru=1.0时的动力p-y曲线骨干曲线可以通过API规范中推荐的砂土p-y曲线乘以折减系数0.16得到，即

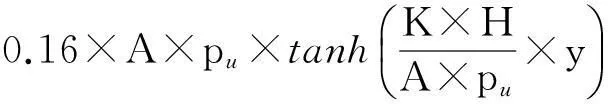
(2)

式中：pu为砂土的极限承载力(kN/m)，取式(3)和式(4)中较小者；A为荷载类型系数，可根据API规范确定[13]；H为计算点深度(m)。按楔体失效理论计算砂土极限承载力pu为：

(3)

按流动失效理论计算砂土极限抗力pu为：

(4)

式中:γ为土体有效容重(N/m3)；D为桩径(m)；C1、C2、C3为计算参数，根据API规范确定[13]。

(2) 孔压比ru<1.0

上述分析可知，当孔压比ru<1.0时，土体动力p-y曲线滞回圈面积很小，加载幅值增至0.25g时，土反力p与极限土反力pult仍然相距甚远，无法拟合获得骨干曲线。然而根据Liu等[14]提出的Cu因子法可知，强度衰减乘因子Cu随孔压比改变呈线性变化(Cu=1-ru)。为构建出统一的动力p-y曲线的骨干曲线，以Cu因子法为基础，假定孔压比ru<1.0时，折减系数随孔压比改变呈线性变化，即折减系数Cz=1-0.84ru，孔压比ru<1.0时的动力p-y曲线的骨干曲线式为：

(5)

以埋深4 m处孔压比ru=0.2和ru=0.6时的动力p-y曲线滞回圈顶点，验证式(5)的有效性(图6)。可见，虽然土反力p和桩土相对位移y均很小，但基本上可以描述出动力p-y曲线的骨干曲线初始刚度。因此式(5)可适用于孔压比ru<1.0时的动力p-y曲线的骨干曲线。

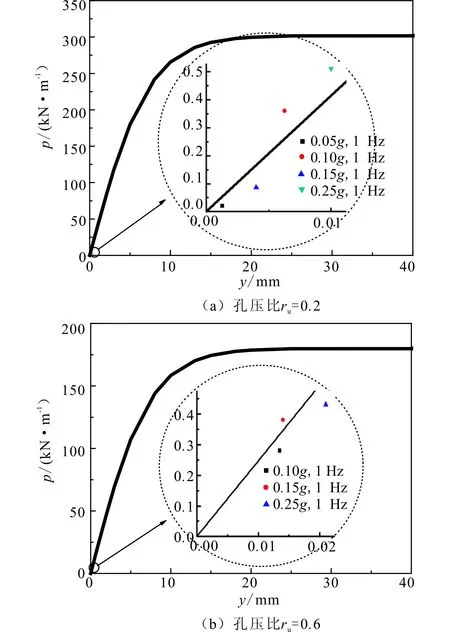
图6　埋深4 m处土体动力p-y曲线的　　　骨干曲线验证Fig.6　Verification of backbone curve of the dynamic　　　 p-y curve at the depth of 4 m

综上，土体动力p-y曲线的骨干曲线表达式为：

(6)

3修正的宏单元模型

Boulanger等[8，15]提出的宏单元模型用于刻画桩-土动力相互作用的物理过程时，需要确定四个计算参数：模型的极限承载力pult、荷载p=0.5pult时的位移y50、最大摩擦力与pult之比Cd和阻尼系数c。通过对这些参数进行修正，将宏单元模型应用于液化场地的桩-土动力相互作用分析中。

3.1基本元件

Boulanger的宏单元模型由弹性单元(p-ye)、塑性单元(p-yp)和裂缝单元(p-yg)串联组成(图7)。

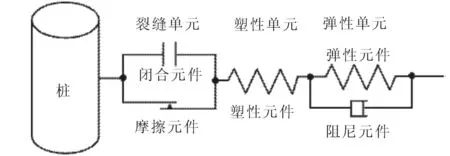
图7　宏单元模型Fig.7　Macro-element model

弹性单元由弹性元件和阻尼元件并联而成。弹性元件的力p与位移关系为

(7)

式中：Ke为弹性元件的切线模量；ye为弹性元件的位移。

塑性单元表示土体的塑性变形。塑性单元和弹性单元串联，二者具有相等的力p。塑性元件中p-yp曲线见图8 (a)，力p按式(8)确定：

(8)

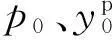
塑性单元的切线模量Kp定义为：

(9)

Matlock(1970)建议，软质黏土取C=10、n=5和Cr=0.35。API规范建议砂土取C=0.5、n=2和Cr=0.2。本文选取API规范给出的建议值。

裂缝单元由一个非线性的闭合元件(pc-yg)和一个非线性的摩擦元件(pd-yg)并联组成。裂缝单元的力p=pc+pd。闭合元件控制着桩-土界面处裂缝的张开和闭合，作用机理与Matlock等[6]提出的黏土p-y属性的裂缝一致。采用摩擦元件描述桩土相对滑动过程中桩受到的侧向摩擦力。闭合元件pc-yg曲线见图8 (b)，摩擦元件pd-yg曲线见图8 (c)。闭合元件的力pc为：

(10)

摩擦元件的力pd为：

(11)

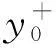
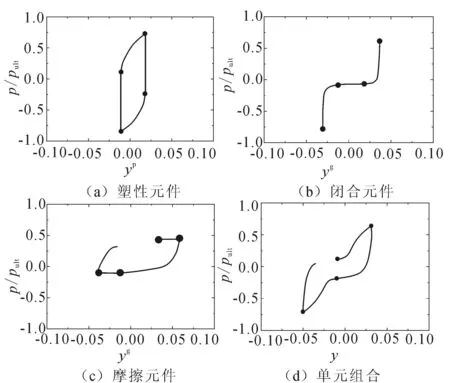
图8　宏单元模型荷载-位移曲线Fig.8　Load-displacement curves of macro-element model

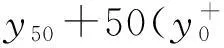
(12)

(13)

裂缝单元的切线模量按式(14)确定:

(14)

3.2组合模式

将上述三种单元串联得到刻画桩-土动力相互作用的宏单元模型[图8 (d)]。模型的位移见式(15)，模型切线模量见式(16)。

(15)

(16)

模型中各元件相互协调发挥作用：当土体在弹性范围内变形，只有弹性元件起作用。随荷载增加，土体进入塑性，弹性元件和塑性元件共同作用。荷载卸载时，桩-土界面处出现裂缝，裂缝单元、弹性单元和塑性单元共同工作。当桩向裂隙移动时，只有摩擦元件发挥作用。

3.3模型参数

通过前述建立的液化场地桩-土相互作用的动力p-y曲线骨干曲线表达式[见式(6)]确定pult和y50，骨干曲线中土反力p的极值即为模型的极限承载力pult，当p=0.5pult时对应的位移即为y50。参照Liyanapathirana[16]的方法，取阻尼系数c=ρvS(vS为剪切波速) 。

最大摩擦力与pult的比值Cd参照Brandenberg等[15]给出的建议值取Cd=1.0。

4简化分析方法与数值模型

4.1数值模型

与三维有限元模型保持一致，基于文克尔地基梁模型，建立桩的简化分析数值模型(图9)。桩采用线弹性梁-柱单元模拟，分24个单元。桩顶节点模拟为集中质量点以模拟上部结构。桩与土的相互作用采用上述动力宏单元模型代替。将动力p-y模型采用2节点(从属弹簧节点和固定弹簧节点)构成的零长度单元表示，将其从属弹簧节点与桩节点的水平方向自由度捆绑在一起。在固定的弹簧节点处输入土体自由场的位移时程作为边界激励条件，完成桩-土动力相互作用的模拟与分析。

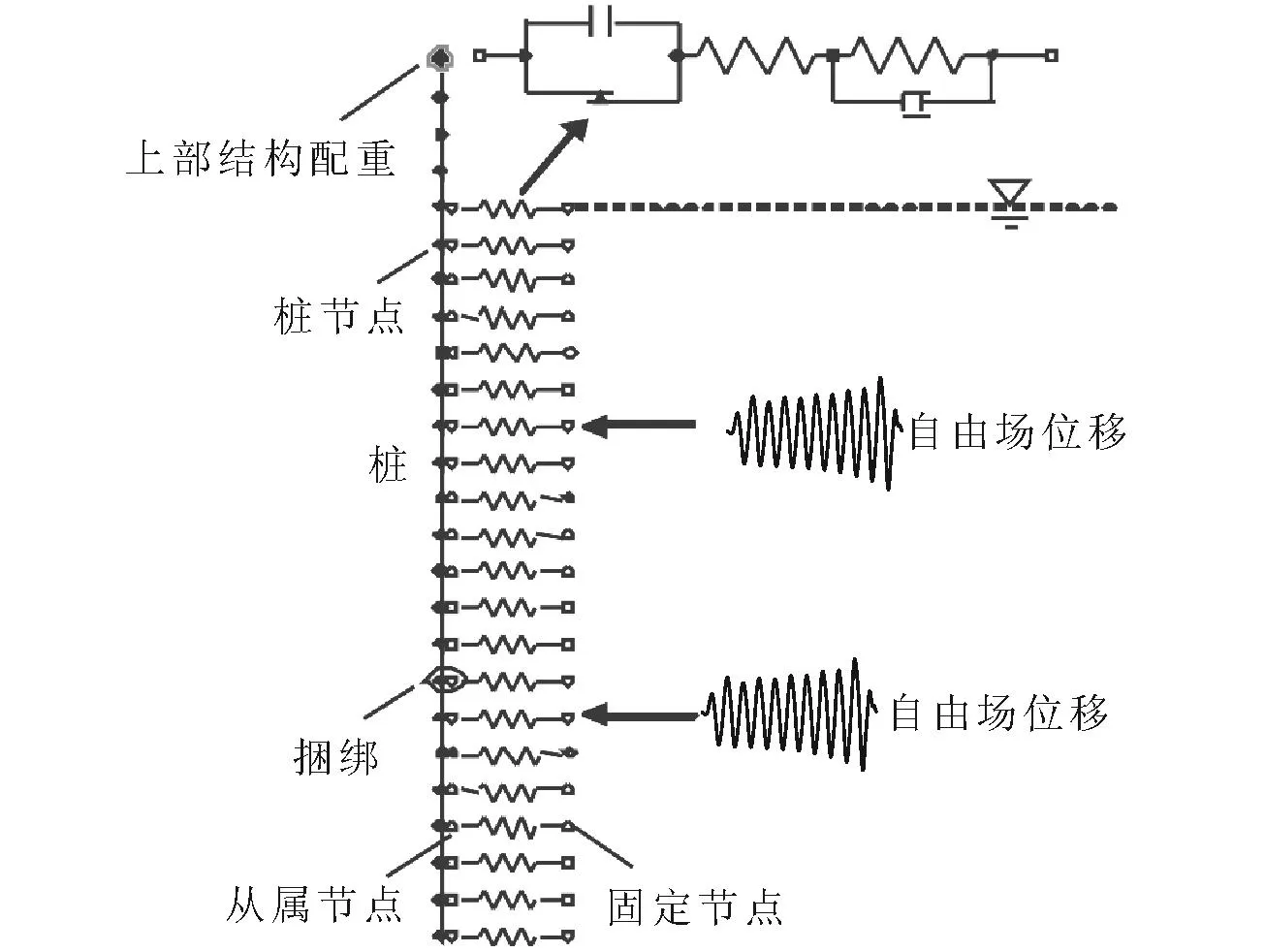
图9　简化分析的数值模型示意图Fig.9　Numerical model for simplified method

4.2外部输入激励

简化分析方法为两部分：(1)进行自由场地的地震反应分析，获得土体的位移和孔压时程，作为简化模型的外部激励；(2)输入外部激励，进行液化场地桩-土动力相互作用的分析。选取El Centro波(图10)进行自由场土体的动力反应分析，得到其位移时程和孔压比时程(图11)。采用简化数值模型，输入自由场土体的位移时程作为外部激励，并通过考虑孔压比改变pult和y50，进行桩-土动力相互作用分析。

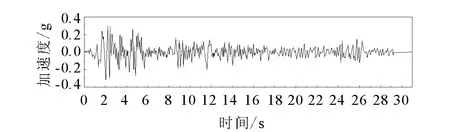
图10　模型基底输入运动Fig.10　Input at model base

4.3简化方法的正确性检验

针对简化数值模型，按照上述参数取值的方法确定各个参数的值，在每一个动力p-y模型的固定弹簧节点输入与其相同埋深处自由场地土体的位移时程，以El Centro波输入下桩的动力特性进行简化分析方法的正确性检验。

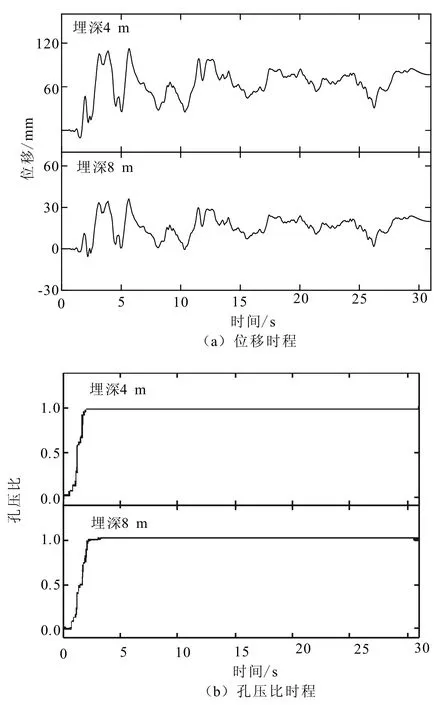
图11　自由场土体位移时程与孔压比时程曲线Fig.11　Displacement time histories and pore pressure　　　 ratio time histories of free field soil

桩的位移是体现桩动力特性的重要指标，它可以通过微分得到桩的加速度。因此桩的位移基本上能体现出桩的动力反应规律。图12为简化方法和有限元法计算得到的不同位置桩的位移时程对比情况。由图可见，两种方法得到的位移时程曲线整体波动趋势基本相同，振动前3 s结果吻合较好，3 s以后简化方法计算得到的结果稍大于有限元法的结果。总之，简化方法基本上能够较好地模拟出更为精细化的有限元法，且其计算时间远小于有限元法的计算机时，所需确定的计算参数也较少，相比而言更适合工程实践的应用。

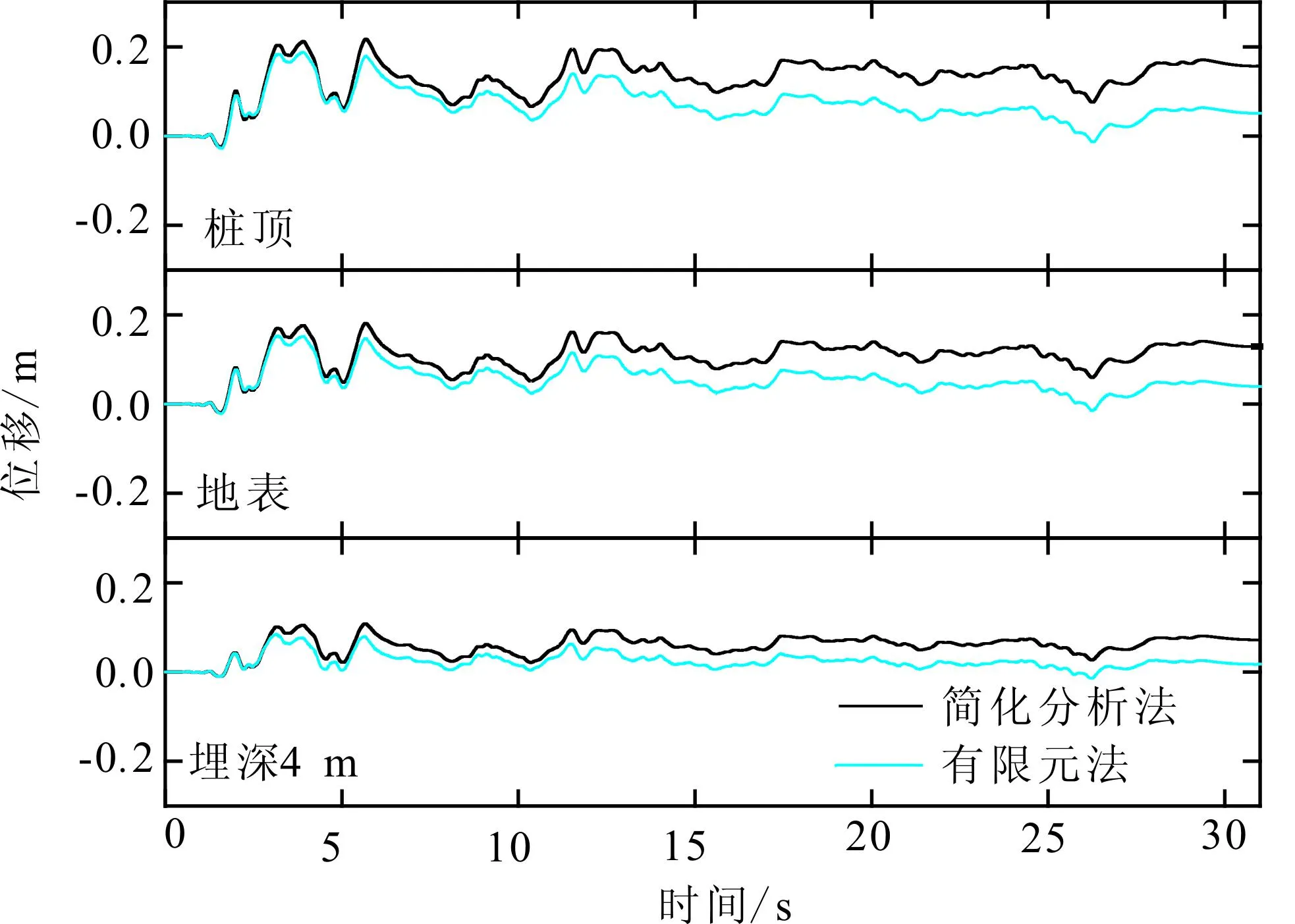
图12　简化方法和有限元法计算结果Fig.12　Results of simplified method and finite element method

5结论

基于液化场地桩-土动力相互作用分析的数值建模途径与计算方法，采用离心机试验标定的内华达砂的动力计算参数，建立液化场地桥梁足尺桩-土动力相互作用三维有限元模型，得到：

(1) 分析不同加载幅值对土体动力p-y曲线影响。结果表明，加载幅值较小时，土体不发生液化，p-y曲线滞回圈面积很小；加载幅值越大，其滞回圈面积越大；当幅值大到一定程度，滞回圈面积不再随幅值的增加发生明显变化，显示土体达到了极限状态。

(2) 通过对API规范中推荐的砂土p-y曲线的计算公式进行修正，得到不同孔压比下液化砂土动力p-y曲线的骨干曲线表达式。

(3) 通过新的液化砂土动力p-y曲线的骨干曲线表达式，改进Boulanger提出的宏单元模型，并将其应用于液化场地的桩-土动力相互作用分析中。

(4) 基于改进的Boulanger模型，提出液化场地桩-土动力相互作用简化分析方法，并验证简化方法的正确性。

参考文献(References)

[1]唐亮.液化场地桩-土动力相互作用p-y曲线模型研究[D].哈尔滨: 哈尔滨工业大学, 2010.

TANG Liang.p-yModel of Dynamic Pile-soil Interaction in Liquefying Ground[D].Harbin:Harbin Institute of Technology,2010.(in Chinese)

[2]张效禹.液化场地桥梁足尺桩-土动力相互作用简化分析方法[D].哈尔滨:哈尔滨工业大学,2011.

ZHANG Xiao-yu.Simplified Method of Dynamic Full-scale Pile-soil Interaction in Liquefying Ground[D].Harbin:Harbin Lnstitute of Technology,2011. (in Chinese)

[3]Kagawa T,Kraft L M.Seismicp-yResponses of Flexible Piles[J].Journal of the Geotechnical Engineering Division,1980,106(GT84):899-918.

[4]Liyanapathirana D S,Poulos H G.Pseudostatic Approach for Seismic Analysis of Piles in Liquefying Soil[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(12):1480-1487.

[5]Sarkar R,Maheshwari B K.Influence of Soil Nonlinearity and Liquefaction on Dynamic Response of Pile Groups[C]//The 14thWorld Conference on Earthquake Engineering.Beijing,China:[s.n.],2008.

[6]Matlock H,Foo S H C.Simulation of Lateral Pile Behavior Under Earthquake Motion[C]//Speciality Conference on Earthquake Engineering and Soil Dynamics.1978,2: 600-619.

[7]Naggar M H,Novak M.Nonlinear Analysis for Dynamic Lateral Pile Response[J].Soil Dynamics and Earthquake Engineering,1996,15(4):233-244.

[8]Boulanger R W,Curras J,Kutter B L,et al.Seismic Soil-pile-structure Interaction Experiments and Analyses[J].Journal of Geotechnical and Geoenvironmental Engineering,1999,125(9):750-759.

[9]唐亮,凌贤长,徐鹏举,等.液化场地桩-土地震相互作用振动台试验数值模拟[J].土木工程学报,2012,45(增刊1):302-306, 311.

TANG Liang,LING Xian-zhang,XU Peng-Ju,et al.Numerical Simulation of Shaking Table Test for Seismic Soil-pile Interaction in Liquefying Ground[J].China Civil Engineering Journal,2012,45(Supp1):302-306,311.(in Chinese)

[10]唐亮,凌贤长,艾哈迈德·艾格玛.液化侧向流动场地桩基动力反应振动台试验三维有限元数值模拟方法[J].土木工程学报,2013,46(增刊1):180-184.

TANG Liang,LING Xian-zhang,Elgamal A.Three-dimensional Finite Element Analysis of Shake-table Test for Dynamic Pile Behavior in Liquefaction-induced Lateral Spreading Ground[J].China Civil Engineering Journal,2013,46(Supp1):180-184.(in Chinese)

[11]Mazzoni S,Mckenna F,Scott M H,et al.Opensees Command Language Manual[R].Berkley:Berkley University of California,2007.

[12]Elgamal A,Lu J,Forcellini D.Mitigation of Liquefaction-induced Lateral Deformation in a Sloping Stratum:three-dimensional Numerical Simulation[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(11):1672-1682.

[13]American Petraleum Institute.Recommended Practice for Planning,Designing and Constructing Fixed Offshore Platforms[M].API Recommended Practice 2A-WSD (RP2A-WSD),2000.

[14]Liu L,Dobry R.Effect of Liquefaction on Lateral Response of Piles by Centrifuge Model Tests[J].National Center for Earthquake Engineering Research Nceer,1995, 9(1):7-11.

[15]Brandenberg S J,Zhao M,Boulanger R W,et al.p-yPlasticity Model for Nonlinear Dynamic Analysis of Piles in Liquefiable Soil[J].Journal of Geotechnical and Geoenvironmental Engineering,2012,139(8):1262-1274.

[16]Liyanapathirana D S,Poulos H G.Sesmic Lateral Response of Piles in Liqufying Soil[J].Journal of Geotechnical and Geo-Environmental Engineering,2005,1(131):1466-1479.

Simplified Seismic Analysis Method for Bridge

Full-scale Piles in Liquefied Ground

ZHANG Xiao-yu1, 2, TANG Liang1, 2, 3, LING Xian-zhang1,2， LI Hui1,2

(1.SchoolofCivilEngineering,HarbinInstituteofTechnology,Harbin150090,Heilongjiang，China;

2.KeyLaboratoryofStructuresDynamicBehaviorandControl,MinistryofEducation,HarbinInstituteofTechnology,

Harbin150090,Heilongjiang，China3.StateKeyLaboratoryofGeohazardPreventionand

GeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,Sichuan，China)

Abstract：Most research in the seismic analysis of pile foundations in liquefied ground is based on small-scale model testing and theoretical analysis. This paper presents the development of a three-dimensional finite element model for dynamic pile-soil interaction using the dynamic calculation parameters of Nevada sand calibrated by conducting the centrifuge test outlined in the Verification of Liquefaction Analysis by Centrifuge Studies (VELACS) project.On the basis of this numerical model, the dynamicp-ycurves under various shaking amplitudes are studied, and a macro-element model for analysis of dynamic pile-soil interaction in liquefied ground is developed. In addition, a simplified method for seismic analysis of the piles on the basis of the Winkler model is presented and verified by the results of numerical simulation.

Key words：macro-element model; simplified method; dynamic full-scale pile-soil interaction; nonlinear finite element analysis; liquefied ground

DOI:10.3969/j.issn.1000-0844.2015.04.0944

中图分类号:TU43

文献标志码：A

文章编号:1000-0844(2015)04-0944-08

作者简介：张效禹(1991-)，男(汉族)，博士研究士，研究方向：岩土工程防灾减灾。E-mail:zxy_hit@163.com。

基金项目：国家自然基金项目(51578195，51378161)；黑龙江省应用技术研究与开发项目(GZ13A009)；国家重点基础研究发展973计划项目(2012CB026104)；地质灾害防治与地质环境保护国家重点实验室项目(SKLGP2013K011)

收稿日期：①2014-08-20