永磁同步电动机的优化设计
蔡黎明,黄开胜,陈文敏,赖文海
(1.广东工业大学,广东广州 510006;2.广东东莞电机有限公司,广东东莞511700)
0 引言
近年来,随着永磁材料以及控制科学的不断发展,加上永磁同步电动机在效率指标和调速性能等方面表现出很大的优势和潜力,调速永磁同步电动机的研究也越来越热门。
本文针对48 槽8 极、1 000r/min 的调速永磁同步电动机齿槽转矩大、振动和噪声大等问题进行优化设计。利用Ansoft 软件基于磁路法的RMxprt 模块建立电动机模型,然后再导入到Maxwell 2D 模块中进行动态仿真,求解出磁极合适的极弧系数和偏心距,在此基础之上求解出每个磁极的最佳偏移角度。仿真结果得出电动机齿槽转矩明显减小。样机测试结果表明电动机的振动和噪声明显削弱,通过削弱齿槽转矩可以使电动机得以优化。
1 齿槽转矩的产生机理及解析分析
永磁电动机的齿槽转矩是电枢铁心的齿槽与转子永磁体相互作用而产生的磁阻转矩[1]。由于电动机定子的齿槽与转子所贴的永磁体相互作用产生的转矩,这个转矩随空间位置作周期性变化,它表现为总是试图将转子定位在某些位置,这个转矩与定子电流无关[2]。
齿槽转矩定义:电动机不通电时,由磁共能产生的转矩。由磁共能产生的转矩可以理解为:在电流为i(i=a,a 为常数)的情况下,磁场能量对转子相对位置角的负导数

式中,W—储存在磁场中的磁共能;θ—定转子之间的相对位置角。
对于永磁电动机来说,储存在磁场中的磁共能W 为

式中,L—转子绕组自感;i—定子绕组相电流;N—定子绕组匝数;Rm—闭合磁路定子铁心的磁阻;R—气隙磁阻;φm—永磁磁通。
把式(2)代入式(1),得

由上式及齿槽转矩的定义可知,气隙磁阻变化引起的磁阻转矩即为齿槽转矩Tcog,其值为


式中,z—槽数;2p—极数;La—铁心长度;对于本次设计的电动机,R1、R2—转子外半径和定子内半径;n—使nz/2p 为整数的转数。
分析式(6)可知,只有Br(θ)的nz/p 次傅里叶系数才对产生齿槽转矩起作用。可通过减小nz/p 次傅里叶系数来减小齿槽转矩。因此,合理选择电动机的极弧系数、磁钢偏心距以及磁极偏移角度等可以降低电动机的齿槽转矩。
2 电动机设计参数及其建模
2.1 主要技术参数
根据公司客户要求的尺寸,本文设计的调速永磁同步电动机的主要技术参数如表1 所示。

表1 电动机的主要技术参数
2.2 建模与剖分
本文采用Ansoft 中的RMxprt 对电动机通过等效磁路法建立样机模型。把生成的模型导入Maxwell 2D 模块进行有限元分析。利用电动机的拓扑结构来减小所仿真电动机的尺寸。为了减小仿真时间,根据本文所设计的电动机的槽极关系,可知仿真电动机模型的1/2 即可。电动机1/2 模型剖分后如图1 所示。

图1 电动机剖分后的1/2 模型
3 电动机齿槽转矩的优化
根据永磁电动机齿槽转矩的产生机理,设置电动机的激励为i=0A。此时,电动机产生的磁共能转矩(亦即齿槽转矩)随时间变化的波形如图2 所示。
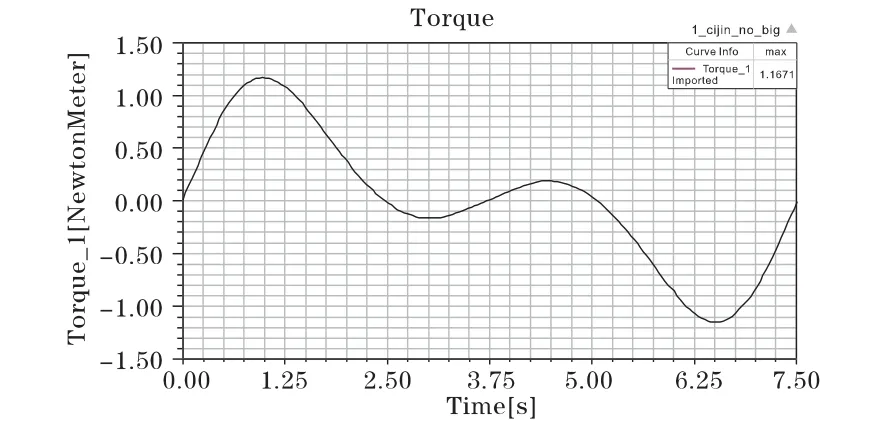
图2 电动机优化前齿槽转矩曲线
由图2 分析可以看出,在没有对电动机进行优化前,该电动机的齿槽转矩的峰值为15.3284N·m。
为了减小齿槽转矩,把转子磁极极弧系数设为变量em,设置Ansoft 为多通道运行方式(根据计算机计算能力选择适当的通道数),采用扫描法得出最佳的极弧系数及其磁钢偏心距,扫描结果如图3所示。从扫描结果可以看出,当em=0.8 时,齿槽转矩最小。

图3 极弧系数扫描
由于极弧系数和磁钢偏心距的参数互不干扰,故在em=0.89 的条件下继续扫描磁钢偏心距。设磁钢偏心距为变量off。扫描结果如图4所示。从扫描结果来看,显然当off=45mm 时,齿槽转矩最小。

图4 磁钢偏心距扫描
由上述二维仿真结果可以看出:当极弧系数为0.89、磁钢偏心距为35mm 时,齿槽转矩较优化前有较大改善。
在得到最佳极弧系数和磁钢偏心距后,为进一步对电动机进行优化,在上述基础之上对电动机磁钢进行偏移,得到各个最佳偏移角。磁钢偏移后如图5 所示。

图5 磁钢偏移后图形
假设磁钢2 和3 向彼此靠拢的角度大小为θ0,且令磁钢2 和3 之间的夹角为θ,设磁钢4的偏移角度大小为θ1。可以建立如下方程式

采用同步扫描法,得到如图6 所示。通过扫描可知,θ0的大小为1。逆时针为正,顺时针为负。

图6 磁极偏移度数扫描
综合以上仿真分析结果,使得极弧系数等于0.89,磁钢偏心距等于35mm,磁钢1 和磁钢2分别偏移-3°、-1°;磁钢3 和磁钢4 分别偏移1°、3°;磁钢5 和磁钢6 分别偏移-3°、-1°;磁钢7 和磁钢8 分别偏移1°、3°。在此条件下,得到电动机的齿槽转矩仿真图,如图7 所示。

图7 优化前后电动机的齿槽转矩
通过以上分析,可以看出电动机在优化前后,齿槽转矩有大幅削弱。根据计算可以得出:齿槽转矩削减了87.7%。
4 电动机的有限元分析
4.1 空载磁密分布
优化后,利用ANSYS 软件的Maxwell 2D 模块对电动机进行分析,得到电动机的磁通密度分布如图8 所示。

图8 电动机的磁通密度分布云图
4.2 空载反电动势及谐波畸变率
利用ANSYS 软件的Maxwell 2D 模块对电动机在不添加激励的情况下进行分析,得到电动机的空载气隙磁密波形,如图9 所示。

图9 电动机空载气隙磁密波形
采用ANSYS 软件自带的FFT 分解器,对电动机的空载气隙磁密波形进行傅里叶分解,得到电动机机空载反电势的谐波分布图,如图10 所示。表2 是对应图10 空载反电势谐波次数及其幅值。

图10 电动机空载气隙磁密FFT 分解

表2 空载子磁场谐波次数及其幅值
把表2 的数据代入式(8)中可以计算空载气隙磁密的谐波畸变率。

式中,n—谐波次数;H—最高次谐波次数;Gn—n 次谐波幅值;G1—基波幅值。
气隙磁密波形质量越高,则永磁电动机的性能越好。本文设计电动机的空载气隙磁密的谐波畸变率为THD=16.53%,说明空载气隙磁密的波形质量较好,电动机的设计及其优化比较合理。
5 样机制作与试验
根据以上分析与仿真,得到48 槽8 极永磁同步电动机理想极弧系数,理想偏心距,以及理想磁极偏移角度,并制作了样机,样机如图11 所示。伺服驱动控制柜如图12 所示。对样机进行试验,试验结果表明,在选择了合理的磁钢偏心距和极弧系数的前提下,按照以上磁极偏移方案试制的样机,其振动和噪声确实有了明显改善。

图11 测试样机图

图12 伺服驱动控制柜
6 结语
本文优化设计了一款48 槽8 极的高功率、大转矩的永磁同步电动机。为削弱电动机的齿槽转矩,利用Ansoft 软件对电动机进行等效磁路法建模和有限元仿真,对样机的极弧系数、磁钢的偏心距以及磁钢的偏移角度进行了优化设计,求解出模型的磁密分布云图和空载气隙磁密波形,并且对空载气隙磁密波形进行了傅里叶分解分析,计算出了样机的空载气隙磁密波形的畸变率。仿真结果和样机测试结果表明电动机的齿槽转矩有明显削弱,噪声也有所降低。
[1] 谭建成.永磁无刷直流电机技术[M].机械工业出版社,2011.193.
[2] 王秀和.永磁电机[M].北京:中国电力出版社,2007.80.
[3] 陈文敏,黄开胜,何良远,等.基于Maxwell 的单相无刷直流电动机分析与设计[J].微电机,2013,46(3):23-26.
[4] 徐英雷,李群湛,王涛.永磁同步电机空载气隙磁密波形优化[J].西南交通大学学报,2009,44(4):513-516.
[5] 车良松,潘柏松,戈道川,等. 轮毂式永磁无刷直流电机空载气隙磁密波形的模拟分析[J]. 机电工程,2011,374-377.

