TLS-ESPRIT 在局部放电窄带干扰抑制中的应用

张宇辉，刘梦婕，段伟润，李天云

（1.东北电力大学电气工程学院，吉林132012；2.国网天津市电力公司，天津300010）

局部放电是造成高压电力设备长期运行中绝缘劣化的重要原因，现场存在的各种干扰信号如连续性周期窄带干扰、脉冲干扰、白噪声干扰等，增大了局部放电信号检测难度，如何削弱这三类干扰的影响，特别是连续性周期窄带干扰，是提高电力设备绝缘状态检测性能的一个关键问题。文献[1-3]采用快速傅里叶变换FFT（fast Fourier transform）处理局部放电信号中的窄带干扰，但FFT 方法受其自身缺陷的影响（如频谱泄露等）导致消噪效果不够理想；文献[4-7]采用小波、多小波变换在抑制窄带干扰方面显示出一定的优势，但其分析结果易受小波类型选取的影响，且经验模态分解完全根据信号自身进行自适应分解，不需要固定的基函数；文献[8，9]将其应用于局部放电信号窄带干扰抑制，取得了较好效果，但模态混叠现象[10]使该算法的稳定性和准确性欠佳。

近年来，一些学者利用混沌系统对与周期策动力频率一致的周期信号敏感的特点，通过判断混沌系统是否发生相变及相变的程度来实现周期窄带干扰信号参数（如幅值等）的估计[11-14]。该方法对局放信号畸变较小，但实际应用中存在灵活性不足的问题：（1）需通过谱分析等手段预先获取窄带干扰的频率；（2）需分别对每个窄带干扰频率预置和调整周期策动力幅值，寻找临界周期状态确定窄带干扰幅值。当检测信号中含有较多窄带干扰时，将会影响混沌振子检测局放信号的效率与准确性。局部放电信号含有多种频率分量，频率范围比较宽[15]，能量比较分散，而周期性窄带干扰信号则与之相反，能量比较集中。

本文在介绍TLS-ESPRIT 理论的基础上，将该方法用于抑制局部放电信号检测中的窄带干扰。通过蒙特卡洛分析研究TLS-ESPRIT 检测多形态局放信号的可行性。

1 TLS-ESPRIT 算法原理与子空间划分

1.1 TLS-ESPRIT 算法

TLS-ESPRIT 是一种处理阵列信号的方法。假设信号可以表示为p 个指数函数的线性组合形式，则定义含有窄带干扰的局部放电信号在采样时刻n 的表达式为

式中：x（n）由窄带干扰信号组成；w（n）由理想局部放电信号组成；ck=akejθk；zk=e（-σk+j2πfk）Ts，Ts为采样周期；ak、θk、σk和fk分别为第k 个窄带干扰分量的幅值、相位、衰减系数和频率；由于采样信号为实信号，p 通常为实际窄带干扰数量的2 倍。

定义Q 个快拍数据为

则

其中：

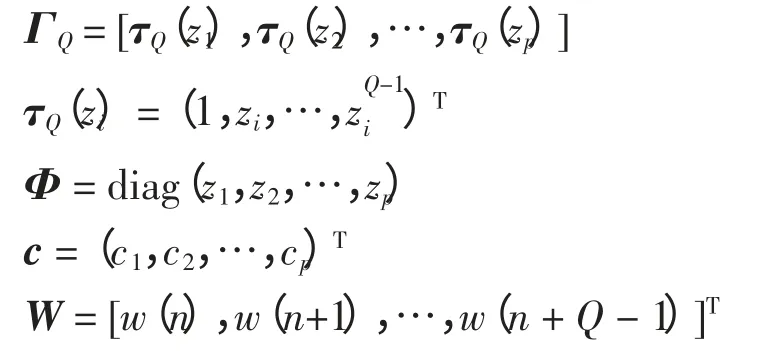
式中，Φ 为旋转算子。

将矩阵B 去除第1 行和最后1 行得到的新矩阵分别定义为B1和B2，则

TLS-ESPRIT 算法步骤[16]如下：

（1）对采样得到的数据序列Y = [y（0），y（1），…，y（Q-1）]T构造HANKEL 矩阵Y(Q-L)×(L+1)，通常L=Q/4～Q/3。

（2）对矩阵H 进行奇异值分解，即

式中，S=diag（ε1，ε2，…，εp，εp+1，…，εmin(Q-1，L+1)）。

利用周期性窄带干扰信号x（n）与局部放电信号w（n）之间的不相关性，以及窄带干扰信号能量比较集中而局部放电信号能量比较分散的特点，按奇异值大小可将V 划分为窄带干扰子空间V1和局部放电信号子空间V2。

（3）令矩阵V1删除第1 行和最后1 行所得到的矩阵分别为V3和V4，则

式中：e1、e2为扰动矩阵（检测信号中存在的放电脉冲和噪声）。使扰动矩阵D=（-e1e2）的Frobenius 范数取得最小值的Φ 即为式（8）的解。对（V4V3）进行奇异值分解，即

对于Q 个采样信号，有

其中：

由最小二乘法得，c=（λTλ）-1λTY，则各窄带干扰分量的幅值和相位为

1.2 窄带干扰子空间V1和局部放电子空间V2的划分

对窄带干扰子空间和局部放电信号子空间的划分即是求HANKEL 矩阵的有效秩p。根据奇异值的大小判断p 值，即

式中：δi为第i 个奇异值；l 可根据奇异值变化曲线设置。满足此条件的i 的最大值记为有效秩。

2 TLS-ESPRIT 算法抑制窄带干扰步骤

基于TLS-ESPRIT 的局部放电信号周期性窄带干扰抑制步骤如图1 所示。将含有窄带干扰的局部放电信号u（t）进行离散采样形成HANKEL 矩阵，对HANKEL 矩阵进行奇异值分解。通过TLSESPRIT 进行窄带干扰参数的提取，得到干扰信号F（t），即

计算u（t）与F（t）之间的差值y（t），则y（t）为抑制窄带干扰后的放电脉冲，即

图1 TLS-ESPRIT 算法抑制窄带干扰步骤Fig.1 Steps for eliminating narrow band noise based on TLS-ESPRIT

3 仿真分析和实测处理

3.1 窄带干扰仿真分析

电力设备中产生的局部放电信号往往具有多种形态，通常选用4 种模型来模拟。

模型1：

模型2：

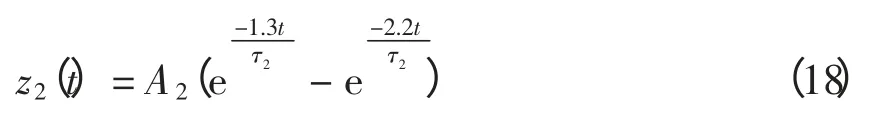
模型3：

模型4：

式中：τ 为衰减系数；fc为振荡频率；A 为信号幅值。模拟4 组放电脉冲，参数均为随机选取。其中，τ1=τ2=1 μs，τ3=τ4=2 μs，fc1和fc2分别为1 MHz 和2 MHz，局部放电信号峰值均为1 mV，采样频率为10 MHz，时域波形如图2 所示。

图2 仿真信号Fig.2 Simulation signals

假设窄带干扰信号f（t）由10 个正弦波叠加而成，频率分别为：80、100、200、300、450、500、620、700、800、980 kHz，各频率成分幅值随机。对叠加80 kHz 窄带干扰的局放信号形成的HANKEL 矩阵进行奇异值分解，结果如图3 所示。

图3 单一频率成分窄带干扰分析Fig.3 Analysis about narrowband noise of the single frequency component

由图3 可知，从第3 个奇异值开始可视为局部放电信号分量引起的奇异值，成功地划分出窄带干扰信号子空间和局部放电信号子空间，存在窄带干扰且窄带干扰个数为1，验证了理论分析的正确性。在图2 原始放电信号基础上叠加窄带干扰f（t），如图4 所示，此时局放信号已被完全淹没。

图4 叠加多种频率成分窄带干扰的信号Fig.4 Signal with multi-frequency narrowband noises

采集局部放电信号形成HANKEL 矩阵，奇异值变化曲线如图5 所示。由图5 可以看出，从第21个奇异值开始，曲线变化趋于平缓。

图5 奇异值变化曲线1Fig.5 Curve 1 of singular value

此时，可将HANKEL 矩阵有效秩取为20，窄带干扰个数为10。采用TLS-ESPRIT 提取窄带干扰参数，计算结果如表1 所示。

表1 窄带干扰参数1Tab.1 Parameters 1 of narrowband noise

抑制周期性窄带干扰后的局放波形如图6 所示，均方误差为2.9×10-3，在窄带数目多达10 的情况下，较好地保留了局放波形特征，有效抑制了窄带干扰。

图6 抑制周期性窄带干扰后的局部放电信号1Fig.6 Partial discharge 1 with eliminated periodic narrowband noise

通过蒙特卡洛分析研究采用本文方法抑制周期性窄带干扰的稳定性，令局部放电信号的衰减系数在100 ns～2.5 μs（步长为50 ns）范围内变化，局放信号、窄带干扰的频率及幅值不变，均独立进行100 次窄带干扰抑制，最终获得的均方误差值如图7 所示。从图7 中可以看出，均方误差在整个衰减系数变化范围内较小，很好地保留了局放波形的振荡特征，也从侧面验证了TLS-ESPRIT 能够实现窄带干扰参数的较高精度估计。

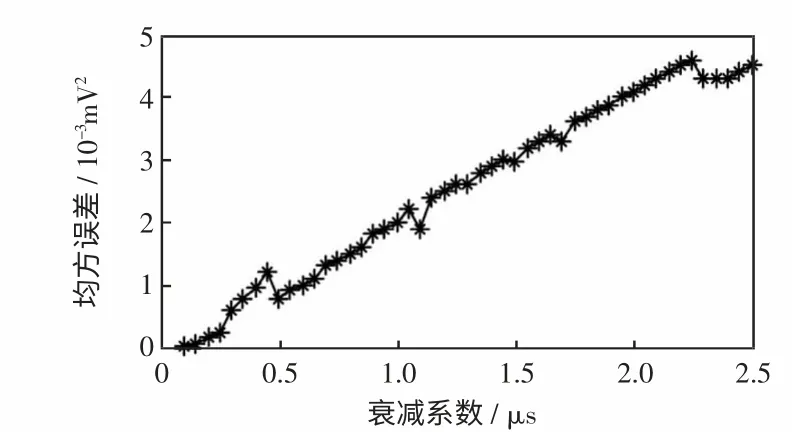
图7 均方误差变化曲线1Fig.7 Curve 1 of mean square error

3.2 随机干扰对抗干扰效果的影响

在图4 的数据上叠加随机白噪声（将随机干扰与理想局放信号视为一个整体），令噪声方差在0.01～0.50（步长为0.01）范围内变化。与第3.1 节相同，独立进行100 次窄带干扰抑制，均方误差的最终结果如图8 所示。从图8 中可以看出，随机干扰程度的逐渐加重导致窄带干扰抑制的效果逐渐变差，但在整个噪声方差变化范围内，本文方法均方误差曲线优于FFT 频域阈值方法曲线，这表明本文方法在很大程度上削弱了随机干扰的影响。

图8 均方误差变化曲线2Fig.8 Curve 2 of mean square error

3.3 考虑采样频率对窄带干扰参数识别的影响

当采样频率fs为100 MHz 时，窄带干扰频率随机设置为500、505、800、805 kHz，1、2、10、20 MHz，信号长度为0.15 ms，数据长度增加到15 000 点，采用FFT 算法的频率估计结果如图9 所示。

图9 FFT 分析结果Fig.9 Results of FFT analysis

为了准确辨识505、805 kHz 窄带干扰，若采用FFT 算法，至少需要0.2 ms 的采样数据。从图9 中可以看出，FFT 算法由于数据窗的宽度较短不能准确辨识出505、805 kHz 窄带干扰。采用TLS-ESPRIT获取的周期性窄带干扰频率值如表2 所示。

表2 窄带干扰频率估计（N=1 500 采样点）Tab.2 Parameters of narrowband noise（N=1 500 Samples）kHz

由表2 可知，TLS-ESPRIT 能够使用较少的数据估计出窄带干扰频率。相比FFT 算法，在减少运算量的同时具有更高的频率识别正确率。

3.4 实测数据分析

图10 为某变电站现场所采集到的一段局部放电信号数据，对其形成的HANKEL 矩阵进行奇异值分解，结果如图11 所示。

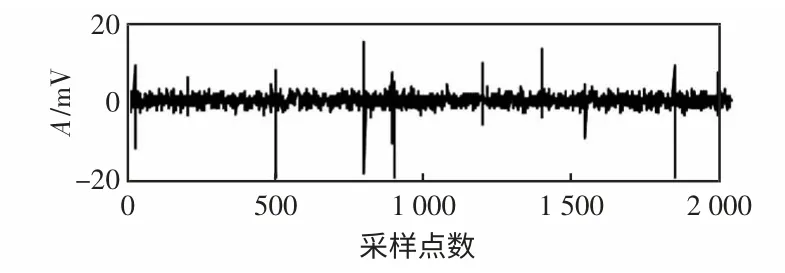
图10 实测信号Fig.10 Measured signal

图11 奇异值变化曲线2Fig.11 Curve 2 of singular value

图11中奇异值变化较为平缓，这表明实测信号受干扰程度较低，无需对其进行窄带干扰抑制。

实测局放信号一般具有非平稳随机过程的特性，针对窄带干扰在频域一个小区间内连续分布的情况，通过人工染噪随机加入6 个频率在310～360 kHz 之间连续分布的窄带干扰信号，叠加干扰后的信号频域波形和时域波形分别如图12 和图13 所示。

图12 实测信号频谱特性Fig.12 Spectral characteristics of measured signal

图13 加入窄带干扰后的实测信号Fig.13 Measured signal with narrowband noise

图14为奇异值变化曲线，从第13 个奇异值开始，奇异曲线变化趋于平缓（P=12）。

采用TLS-ESPRIT 获取的周期性窄带干扰参数如表3 所示。

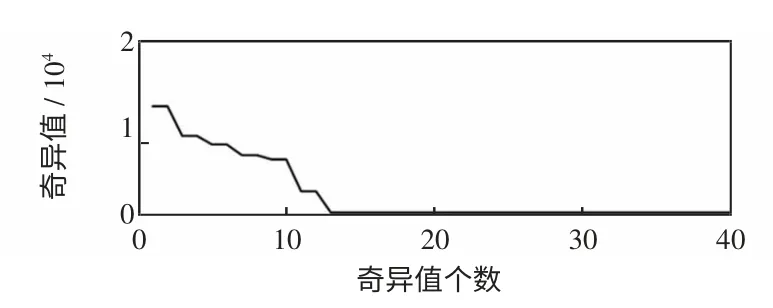
图14 奇异值变化曲线3Fig.14 Curve 3 of singular value

表3 窄带干扰参数2Tab.3 Parameters 2 of narrowband noise

采用本文方法抑制窄带干扰后的结果如图15所示。比较图13 和图15 可以看出，本文方法能很好地保留局放信息和抑制窄带干扰。

图15 抑制周期性窄带干扰后的局部放电信号2Fig.15 Partial discharge signal 2 with eliminated periodic narrowband noise

4 结论

（1）TLS-ESPRIT 算法能够在较短的数据窗内有效辨识出局部放电信号中主要窄带干扰参数，减小了运算量；对局放信号本身具有一定的免疫力，且抗随机干扰能力较强，为处理多种形态的局部放电信号提供了一种新思路。

（2）对窄带干扰子空间数据进行矩阵运算，直接求取各窄带干扰参数，相比混沌振子方法易实现、灵活性强。

（3）用奇异值变化曲线估计局放信号的受干扰程度，能为是否需要进一步去除窄带干扰给出定量的估计判断，避免因盲目去噪导致局放信号波形特征的丢失。

[1]谢良聘，朱 德恒（Xie Liangpin，Zhu Deheng）. FFT 频域分析算法抑制窄带干扰的研究（Research of spectrum analysis based on FFT for suppressing narrow-band interference in PD signal）[J]. 高电压技 术（High Voltage Engineering），2000，26（4）：6-8.

[2]卢毅，韩志锟，陈瑜（Lu Yi，Han Zhikun，Chen Yu）. 基于能量比预处理的FFT 窄带滤波方法 （FFT narrow band filtering method based on energy-ratio pretreatment）[J]. 东南大学学报（Journal of Southeast University），2010，40（5）：948-951.

[3]徐剑，黄成军（Xu Jian，Huang Chengjun）. 局部放电窄带干扰抑制中改进快速傅里叶变换频域阈值算法的研究（Research on improved fast Fourier transform algorithm applied in suppression of discrete spectral interference in partial discharge signals）[J]. 电网技术（Power System Technology），2004，28（13）：80-83.

[4]Satish L，Nazneen B. Wavelet-based denoising of partial discharge signals buried in excessive noise and interference[J]. IEEE Trans on Dielectrics and Electrical Insulation，2003，10（2）：354-367.

[5]Zheng W，Zhou X，Xu H，et al.Partial discharge signal obtain based on adaptive wavelet with mathematical morphology[J].Physics Procedia，2012，24（Part B）：912-917.

[6]王立欣，诸定秋，蔡维铮（Wang Lixin，Zhu Dingqiu，Cai Weizheng）. 局部放电在线监测中基于小波变换的阈值消噪算法研究 （Wavelet transform based de-noise algorithm by thresholding in on-line partial discharge detection）[J]. 电网技术（Power System Technology），2003，27（4）：46-48，78.

[7]钱勇，黄成军，陈陈，等（Qian Yong，Huang Chengjun，Chen Chen，et al）. 多小波消噪算法在局部放电检测中的应用（Application of multi-wavelet based on denoising algorithm in partial discharge detection）[J]. 中国电机工程学报（Proceedings of the CSEE），2007，27（6）：89-95.

[8]沈宏，张蒲，徐其惠，等（Shen Hong，Zhang Pu，Xu Qihui，et al）. 基于经验模态分解和自适应噪声对消算法的窄带干扰抑制（Narrow-band interference suppression based on adaptive noise canceller and empirical mode decomposition）[J]. 高压电器（High Voltage Apparatus），2009，45（1）：8-14.

[9]姚林朋，黄成军，钱勇（Yao Linpeng，Huang Chengjun，Qian Yong）. 基于EMD 的局部放电窄带干扰抑制算法（Empirical mode decomposition based DSI suppression algorithm in partial discharge detection）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（5）：33-38.

[10]王宏，Narayanan R M，周正欧，等（Wang Hong，Narayanan R M，Zhou Zhengou，et al）.基于改进EEMD 的穿墙雷达动目标微多普勒特性分析 （Micro-doppler character analysis of moving objects using through-wall radar based on improved EEMD）[J]. 电子与信息学报 （Journal of Electronics & Information Technology)，2010， 32 （6）：1355-1360.

[11]李楠，廖瑞金，孙才新，等（Li Nan，Liao Ruijin，Sun Caixin，et al）. 一种用混沌振子去除局部放电信号中窄带干扰的新方法 （A new suppression method for narrow-band interference in partial discharge signals with chaotic oscillator)[J]. 电工技术学报（Transactions of China Electrotechnical Society)，2006，21（2)：88-92.

[12]舒娜，张晓星，孙才新，等（Shu Na，Zhang Xiaoxing，Sun Caixin，et al）. 采 用Van-der 混沌振子抑制局部放电信号中周期性窄带干扰（Van-der chaotic oscillator to suppressing the periodic narrow-band interference from partial discharge pulse signal)[J]. 高电压技术（High Voltage Engineering)，2012，38（1）：89-94.

[13]臧怀刚，郭小星，李小俚（Zang Huaigang，Guo Xiaoxing，Li Xiaoli）. 基于混沌控制和多重滤波的局部放电去噪研究（De-noising of partial discharge based on chaotic control and multiple-filter）[J]. 电力系统保护与控制（Power System Protection and Control），2011，39（5）：86-90.

[14]周力行，李卫国，邓本再（Zhou Lixing，Li Weiguo，Deng Benzai）. 基于混沌控制的周期窄带干扰抑制方法研究（Study of suppressing the periodic narrow bandwidth noise in partial discharge detection based on chaotic control）[J].高电压技术（High Voltage Engineering），2004，30（10）：39-41.

[15]刘卫东，刘尚合，王雷（Liu Weidong，Liu Shanghe，Wang Lei）. 采用Gabor 变换的局部放电信号时频分析（Timefrequency analysis of partial discharge signal by Gabor transform）[J]. 高电压技术（High Voltage Engineering），2007，33（8）：40-43.

[16]周云钟，陈天麒（Zhou Yunzhong，Chen Tianqi）. 一种自适应ESPRIT 算法（An adaptive ESPRIT algorithm）[J].系统工程与电子技术（Systems Engineering and Electronics），2001，23（9）：5-8，11.