基于灵敏度法的SMES 安装位置实用化方法

苗友忠，罗 玮，游昌清

（1.国网冀北电力有限公司，北京 100053；2.天津天大求实电力新技术股份有限公司，天津 300384）

在电力系统电压稳定性研究领域，有一类特殊的电压波动现象，是系统因雷击、短路等故障而进入暂态过程，在故障元件切除后的暂态过程中，系统虽然是稳定的，但系统中某些母线的电压在暂态过程中短时间地（数十毫秒到数秒）处于较低的数值[1]，这种现象称为晃电。显然，故障后一段时间的低电压水平会导致在这些母线上的电压敏感类负荷不能正常工作。如恒转矩负载感应电动机发生堵转[2]、放电等现象，从而破坏企业配电网的安全运行。超导储能SMES（superconducting magnetic energy storage）是对于瞬时电压跌落问题的一种解决方案[3]。由于SMES 自身四象限功率运行、能量密度大、转换效率高、发出的有功无功可以独立控制的特点，其安装位置的实用化方法不同于传统的柔性交流输电系统FACTS（flexible alternative current transmission systems）安装地点的选择。同时，SMES 的价格比较昂贵，在应用SMES 进行配电网晃电治理中必须严格限制其容量并优化安装地点以达到最优的控制效果。

超导储能装置由于具有快速响应特性[3，10]，因而不仅能用于调节峰值，而且可以储存应急的备用电力，提高容许输电容量和系统的稳定性，改善供电质量。在对SMES 外特性进行分析中，已有文献往往是将其看作能与电网交换有功功率的灵活交流输电系统（FACTS）装置。国内外有很多学者研究FACTS 在系统中的布局问题，并得出了很多结果，其中SMES 在电力系统中最优布局问题上，Ohsawa 等[4]利用系统的特征向量来决定SMES 的布局，Ueda等[5]采用Tabu 算法求SMES 模块的最优布局，Wada 等[6]采用遗传算法求解SMES 的最优布局，Sang-Joong[7]以系统损耗最小化为目标求解SMES 最优布局，另外还有利用求解FACTS 装置对发电机输出功率的影响来选择安装点的方法。即使在线性条件下，要将这些方法应用到大规模电力系统也是相当困难。传统的模态分析法基于全系统状态方程矩阵特征根的求取，当系统阶超过20 时，QR 算法可能不收敛。同时，以上涉及的方法不能反映由特定扰动激发的具体模式以及非线性对大扰动稳定性的影响，从而忽略了扰动对安装地点的影响作用。文献[8-11]从改善系统暂态稳定水平的角度，提出了临界能量相对于网络参数变化的灵敏度分析方法，但却未对暂态稳定的故障相关性给予充分的考虑。事实上，非自治非线性系统的暂态稳定分析必须针对整个故障序列，包括故障清除后的系统方程进行完整的积分。数值积分虽然能给出精确的受扰轨迹，但无法对后者的稳定性给出量化指标，因此也就难以定量评估同一SMES 装置装设在不同地点时的控制效果。

如果只是单独使用仿真分析的方法，来解决超导磁储能装置的安装选址问题，仿真计算量大且繁杂，仿真结果因选取参数的影响，在结果相差不明显时，很难进行精确的比较。目前，现代的电力系统分析方法主要使用基于计算机分析的潮流程序来实现，然后采用数学理论的方法来模拟和分析。本文将在状态方程及潮流程序分析的基础上，着重于系统精确的暂态过程分析，引入了灵敏度系数，对典型企业配电网中的SMES 装置安装选址进行理论分析及推导，提出解决实际配电系统网络中的超导磁储能装置安装选址问题的实用化方法。

1 灵敏度方法

灵敏度是利用系统中某些物理量的微分关系，来获得因变量对自变量敏感程度的方法。根据灵敏度结果提供的信息，指导自变量的调整，从而控制因变量的改变。具体而言，可以根据灵敏度指标采取一系列措施，使因变量的改变达到预期的效果，从而改善系统的安全性能，提高系统稳定裕度或经济性指标。灵敏度方法在诸多领域中得到了广泛的应用。假设用于灵敏度分析的系统数学模型[12]为

式中：x 为状态变量；y 为代数变量；λ 为系统的参数变量。系统的初始条件为

对于初始条件式（2），系统式（1）的解为

参数λ 的变化会导致系统的时域轨迹发生变化。考虑最简单的单参数情形，为得到x（t）和y（t）对单参数的灵敏度，将式（1）对参数λ 进行微分，则有

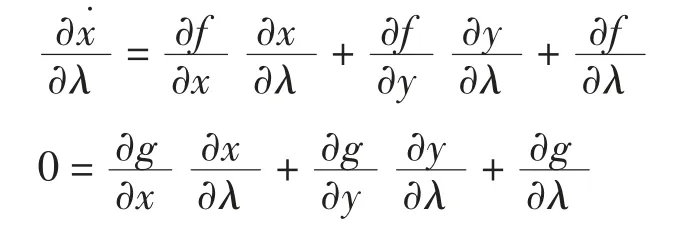
即

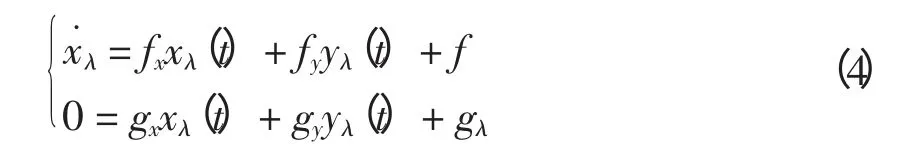
式中：fx、fy、fλ和gx、gy、gλ均是不显含t 的确定性函数；xλ（t）和yλ（t）分别为状态轨迹和代数变量轨迹对参数λ 的灵敏度。式（4）为式（1）的轨迹灵敏度方程。其定解条件为

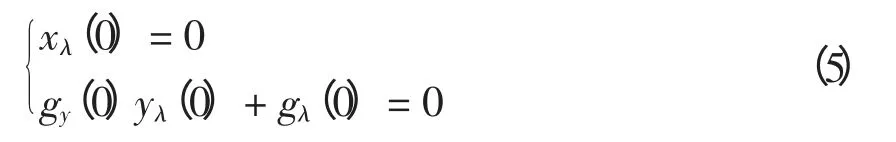
由此可知，求解式（1）和式（4）组成的微分代数方程组即可得到轨迹灵敏度xλ（t）和yλ（t）

由轨迹灵敏度的意义可知，对于充分小的参数增量Δλ 有

从式（6）可见，轨迹灵敏度xλ（t）和yλ（t）是随时间变化的连续曲线，它反映了参数变化所引起的状态变量和代数变量的轨迹在时刻t 的变化程度。

2 灵敏度方法在SMES 选址中的应用

SMES 的安装地点的选择可以看作一种动态无功补偿的规划问题。最理想的结果是对于电力系统相应运行工况任意扰动，SMES 在所选择的安装地点能给电力系统提供高效、合理的无功功率的动态平衡，缓解扰动，特别是非发电机连接母线的扰动对电力系统的电压质量造成的冲击。从这个角度分析，SMES 属于一种局部的动态反馈设备，其作用有两点：①减小电力系统中的扰动波及面；②提升电力系统母线电压自持能力。由此可知，SMES 的选址问题必须涉及到电力系统的潮流结构和母线特性两个方面。电力系统稳定性分析中采用的分析方法都可以为SMES 的选址提供一定的理论支撑。潮流分析法可以提供相应运行工况下电力系统的无功功率分布情况；特征结构分析法可以提供特定运行工况下的平衡点稳定性，对于扰动后的电力系统动态特性提供有意义的预测估计等。

综上分析，可以得到在实际的复杂电力系统网络中应用SMES 设备安装选址的一般性方法。其基本思路是在潮流计算的基础上，选择在晃电故障情况中容易受影响的节点，并且该节点要对整个系统具有明显的控制系数。这样，在SMES 设备接入后，就能快速、显著地在系统的暂态过程中发挥作用，最大程度改善系统的暂态稳定性能，如图1 所示。

其选址方案的初始步骤如下：

步骤1 对于给定具体的电力系统网络，列出其发电机、变压器及线路和负载参数；

步骤2 对给定的系统稳定运行的情况生成系统的导纳矩阵，进行潮流计算，求出系统中各个发电机节点和负荷节点的电压、电流和功率的稳态值；

步骤3 根据负荷电压静特性参数，由已知的各负荷的功率及负荷的节点电压稳态值，求出负荷线性化状态方程中各个矩阵的元素，并用它们修改相应的导纳矩阵中对应于各个负荷矩阵的对角阵子块。由各个发电机节点电压、电流稳态值，依次计算出相应的各发电机组中所有变量的初值；

步骤4 列出全系统的线性化状态方程。计算除去发电机节点和变压器线路的各个节点/线路的控制系数，选择出若干具有明显控制效果的节点；

步骤5 最终得出在理论上安装SMES 设备作用明显的系统节点集合。

图中的阴影部分面积表征了节点的电压在晃电问题所关注的时段（t0，t1）内的改善程度。阴影部分面积为

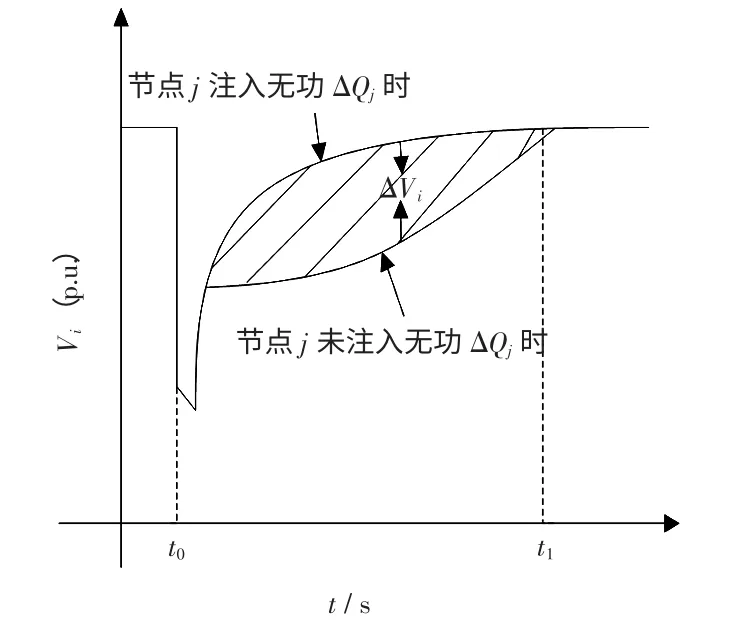
图1 注入无功功率对晃电的影响Fig.1 Effect of injection of reactive power on the akira power

式（7）表示在节点j 注入ΔQ 的无功功率前后，节点i 电压变化曲线Vi在时刻区间（t0，t1）上的积分。

显然：

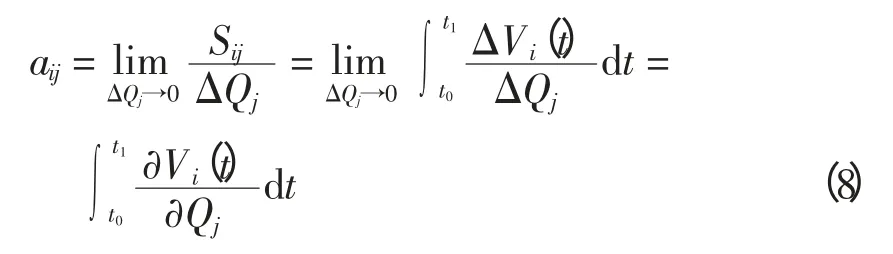
式中：Vi为节点i 的电压；Qj为节点j 的无功功率注入；aij为在节点j 进行无功补偿时对节点i 的电压改善程度。由电力系统无功注入与系统电压的一般关系可知，aij〉0。

设m 个备选安装节点j 的集合为J，就改善节点i 的电压而言，所有备选安装节点中值最大的那个节点即是最佳的无功补偿地点。设受晃电影响的所有节点的集合为I，包含n 个元素。n 个节点的电压需要有节点处安装的SMES 装置发出的无功补偿来改善。节点j 处安装无功补偿的有效性可以由灵敏度指标SIj确定，且有

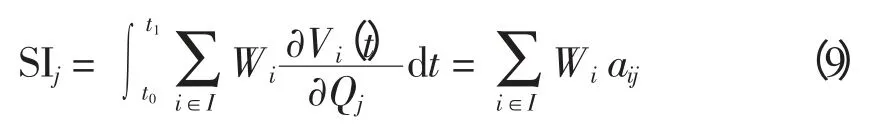
式中，Wi为权系数，它表征了对节点i 的电压水平的重视程度。SIj值越大，代表该节点安装SMES 越有效。由于灵敏度曲线是连续的，因而在数值计算时需要对其离散化。为此，将晃电时段（t0，t1）分成l个时段，则有

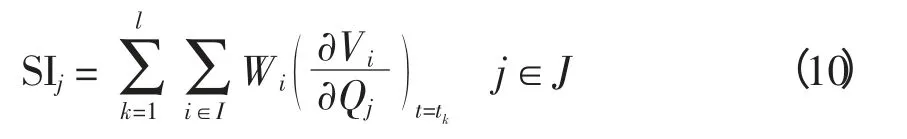
式中，tk为灵敏度法的采样时刻。

SMES 的选址实用化方法的步骤如下：

（1）确定受晃电影响的节点集合I。

（2）根据初始步骤确定待选的SMES 安装节点集合J。在选择是通常不考虑发电机节点和已装有大量无功补偿的节点，也不考虑那些由于环境等因素而不适合安装无功补偿装置的节点。

（3）对i∈I 和j∈J，通过对式（1）和式（4）进行数值积分，计算各灵敏度的数值解。

（4）由式（10）计算m 个灵敏度指标SIj。

（5）选择SIj值最大的节点作为SMES 装置的最佳安装地点。

3 算例验证

在PSASP 中搭建某大型企业配电网，电网结构如图2 所示。并且建立基于PI 控制[13]的SMES自定义模型如图3 所示。考虑到SMES 价格昂贵和企业电网电气距离较短，只安装一台SMES。根据潮流计算结果选择母线上的敏感负荷较多的653和651 母线为待定安装节点。开关655 模拟的是高压快切装置，正常情况为断开状态。653 和651母线电压等级为6 kV，651 母线所带负荷为油循，653 所带负荷为PTA（pure terephthalic acid），二者对电压的稳定要求很高，电压波动不允许超出额定电压的±5%，即95%～105%。单独在651 母线和653 母线上安装容量为10 Mvar 的SMES 进行仿真验证。

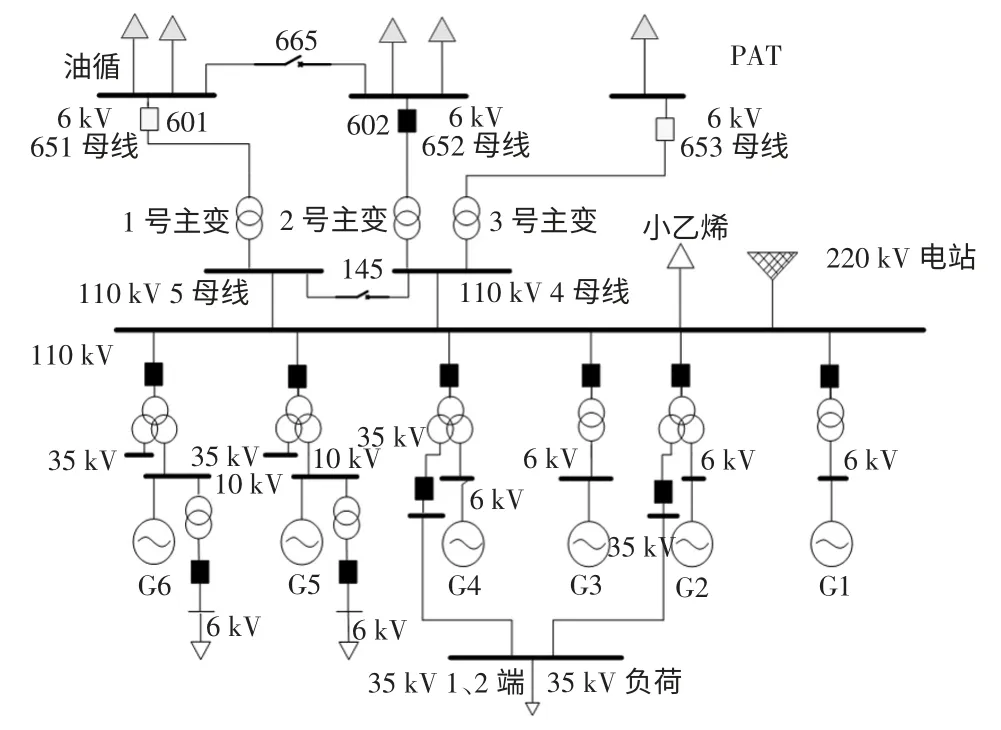
图2 仿真分析用简化电网结构Fig.2 Simplified grid structure for simulation analysis

考虑如下两种故障情况[14]：

故障1 母线651 所带油循2 在2.0 s 时发生25%的负荷冲击，持续时间0.2 s。

故障2 母线653 所带PTA 在2.0 s 时发生25%的负荷冲击，持续时间0.2 s。

根据表1 的计算结果，可看出故障计算结果。

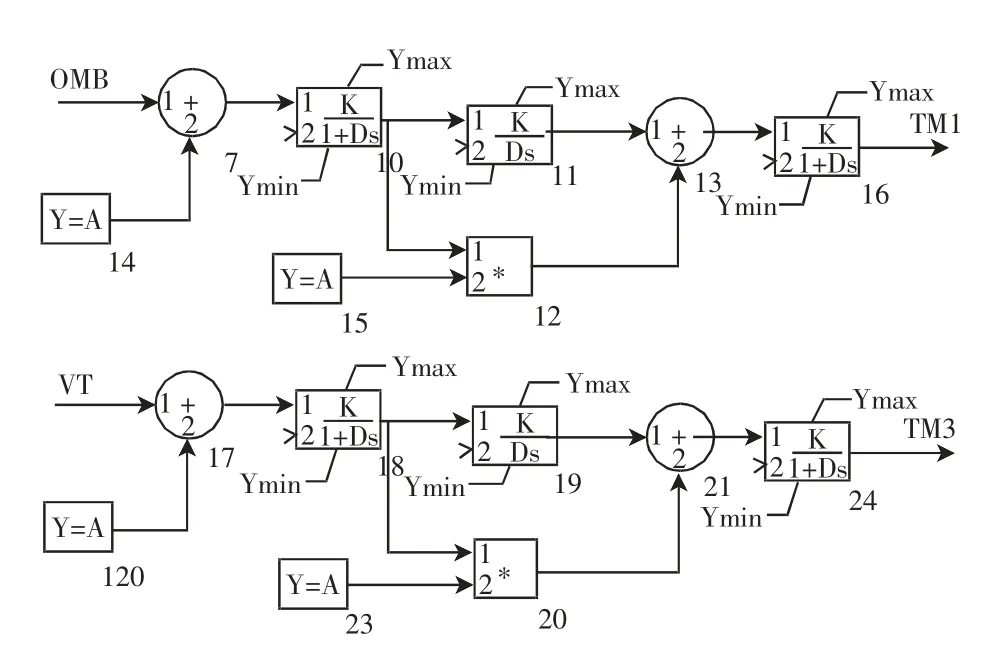
图3 基于PI 控制的SMES 模型Fig.3 SMES model based on PI control

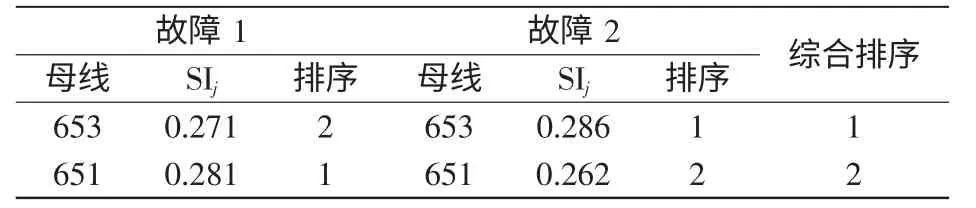
表1 故障计算结果Tab.1 Fault calculation results

故障1 的情况下653 母线的SIj值小于651母线，在故障2 的情况下653 母线的SIj值大于651 母线。即故障1 情况下，SMES 安装在651 母线优于安装在653 母线；在故障2 情况下，SMES 安装在653 母线优于安装在651 母线。出现这种情况是由于在无功补偿装置就近补偿原则下，距离补偿装置越近的母线其补偿效果越好，同时SIj的值就越大。通过数值分析，综合两种故障653 母线SIj的值大于651 母线的值，即653 母线的综合灵敏度值大于651 母线。在安装一台SEMS 装置的情况下，SMES 安装在653 母线上的综合效果优于安装在651 母线上。

故障1 时在651 母线处和故障2 时在653 母线处安装SEMS 时母线电压如图4 和图5 所示。

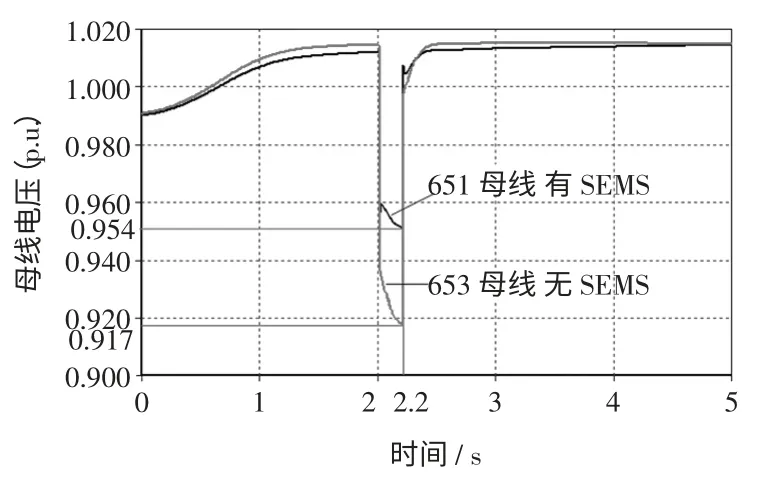
图4 故障1 时母线电压Fig.4 Bus voltages of fault one

通过仿真对比图4 与图5，故障1 与故障2 的故障类型相似，在SMES 装置的补偿作用下故障母线的电压最低值都分别为0.954 和0.955，SMES 装置安装在653 母线上时，651 母线的最低电压达到0.925。SMES 装置安装在651 母线时，653 母线的最低电压为0.917。可以得到，母线电压对SMES 安装于653 母线更为敏感。从而验证了本文所述方法的正确性。

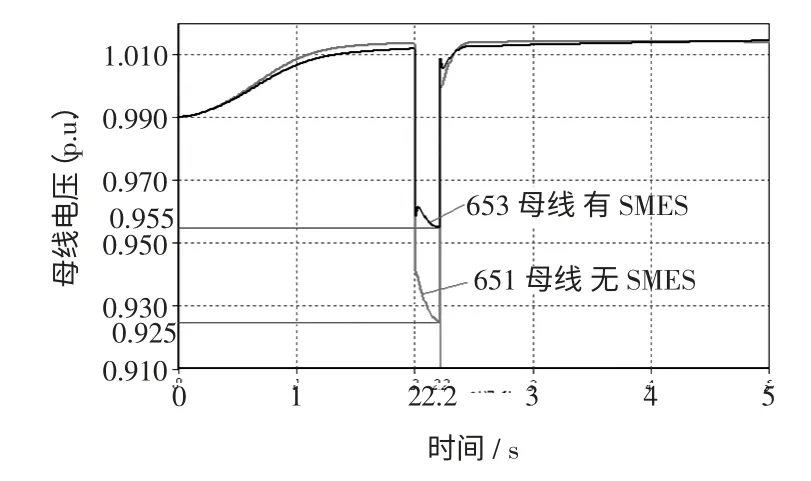
图5 故障2 时母线电压Fig.5 Bus voltages of fault two

4 结语

本文在灵敏度分析的基础上建立了SMES 装置安装地点灵敏度指标，提出了基于灵敏度指标进行SMES 安装地点选择的方法。通过实际企业配电网的仿真，在单台SMES 约束的情况下验证了提出方法的正确性，为SMES 装置的工程应用提供了一定的指导。

[1]Peng Wang，Billinton R，Goel L. Probability distribution evaluation of distribution system reliability indices using a time sequential simulation technique[C]//Canadian Conference on Electrical and Computer Engineering. Halifax，Canada，2000：760-764.

[2]Taylor L Y，Shih-Min Hsu. Transmission voltage recovery following a fault event in the Metro Atlanta area[C]//Power Engineering Society Summer Meeting.Seattle，USA，2000：537-542.

[3]Parizh M，Kalafala A K，Wilcox R. Superconducting magnetic energy storage for substation applications[J]. IEEE Trans on Applied Superconductivity，1997，7（2）：849-852.

[4]Ohsawa Y，Maruoka Y，Takeno H，et al. Determination of installation location of SMES for power system stabilization[C]//IEEE International Symposium on Circuits and Systems.Geneva，Switzerland，2000：233-236.

[5]Ueda S，Takeuchi H，Ohsawa Y，et al. Studies on power system stabilization by distributed allocation of micro SMES units[C]//International Conference on Power System Technology.Piscataway，USA，2002：1244-1248.

[6]Li Yuan-Zhi，Wada K，Oshawa Y，et al.Optimal allocation of micro SMES units for power system stabilization by means of genetic algorithm[C]//International Conference on Power System Technology.Chongqing，China，2006.

[7]Sang-Jong Lee. Location of a superconducting device in a power grid for system loss minimization using loss sensitivity[J].IEEE Trans on Applied Superconductivity，2007，17（2）：2351-2354.

[8]Zhao J，Ishigame A，Kawamoto S，et al. Structural control of electric power networks for transient stability[J]. IEEE Trans on Power Systems，1994，9（3）：1575-1581.

[9]Choudhry M A，Reza M A，Ellithy K A. Design of a robust modulation controller over a wide range of load characteristics for AC/DC systems[J].IEEE Trans on Power Systems，1990，5（1）：212-218.

[10]王永贵，卫志农，孙国强，等（Wang Yonggui，Wei Zhinong，Sun Guoqiang，et al）.基于轨迹灵敏度和FASTICA的同调机群识别方法（Method of identifying coherent generator groups based on trajectory sensitivity and FASTICA）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（3）：14-19.

[11]Xu L，Ahmed-Zaid S. Tuning of power system controllers using symbolic eigensensitivity analysis and linear programming[J]. IEEE Trans on Power Systems，1995，10（1）：314-322.

[12]方家琨，苗璐，文劲宇，等（Fang Jiakun，Miao Lu，Wen Jinyu，et al）.含风电-SMES 的电力系统暂态稳定概率评估（Transient stability probability evaluation of power system incorporation with wind farm and SMES）[J]. 电力系统保护与控制（Power System Protection and Control），2013，41（1）：176-182.

[13]Rouco L，Pagola F L.An eigenvalue sensitivity approach to location and controller design of controllable series capacitors for damping power system oscillations[J].IEEE Trans on Power Systems，1997，12（4）：1660-1666.

[14]Eliasson B E，Hill D J. Damping structure and sensitivity in the NORDEL power system[J].IEEE Trans on Power Systems，1992，7（1）：97-105.