Kriging插值和有限元插值在工程问题中的对比

摘要：文章首先给出了Kriging插值和有限元插值的原理，然后用两种方法分别对三维体电阻率进行插值，并将插值结果进行三维成像，比较两种插值算法的效果，其结果是有限元插值效果优于普通Kriging插值，且算法复杂度和计算量相对较小，最后探讨了两种插值算法在工程上的推广。

关键词：空间插值；有限元插值；Kriging插值；电阻率插值；数据三维成像 文献标识码：A

中图分类号：O241 文章编号：1009-2374（2015）36-0057-03 DOI：10.13535/j.cnki.11-4406/n.2015.36.027

在工程实践中，考虑到成本和测量技术等原因，通常无法对一个物体进行密集测量，只能获得部分测量数据，这些数据往往不能满足研究的需求。因此，需要用科学、合理的方法对数据进行扩充。数据扩充可以通过补充测量和插值来完成。前者需要投入大量的时间和金钱；后者虽然存在一定误差，但可以节省大量人力物力，并能满足一般工程问题的精度要求。由于工程中研究的对象大多是三维实体，需要扩充的数据也是空间数据，因而研究空间数据插值方法对实践具有重要指导作用。本文介绍了地统计学中应用较多的Kriging插值和力学分析中广泛使用的有限元插值，并用两种方法分别对空间电阻率进行插值，将插值结果进行三维成像，从而对比其在工程问题中的效果，分析其在其他领域的推广可行性。

1 空间插值的概念及分类

空间数据插值是用已知点的数据来估算、预测未知点数据的过程。按插值范围可分为空间内插和空间外推。内插是通过已测量点的数据推求区域内未测量点的数据，外推则是推求区域外的数据。本文分析的Kriging插值和有限元插值是两种典型的内插算法。

2 有限元插值方法概述

有限元插值的核心在于单元和插值函数的构造，即选择合适的单元结构，并构造待插区域的插值多项式，然后利用节点条件，将插值多项式的待定参数表示成节点值和单元几何参数的函数，即得到形函数，然后构造出插值函数。下面以六面体单元为例介绍有限元插值函数的构造方法：

2.1 建立局部坐标系

设局部坐标系为（ξ，η，ξ），任意六面体的顶点为

（i=1，2…，8），如图1。首先利用双向距离坐标，把四边形变换成坐标面上的单位正方形，把变换成坐标面上的单位正方形。然后把两个单位四边形中具有相同局部坐标的点连成线段，最后沿线段方向从下到上定义距离坐标，和上的单位正方形上的点的分别为0和1。于是六面体上任意一点的局部坐标可表示为（ξ，η，ξ）。至此，坐标系中任意六面体单元与局部坐标系中的单位立方体之间建立了一一对应关系。

2.3 写出插值函数

3 克里金（Kriging）插值方法概述

Kriging插值又叫空间自由协方差最佳内插，其原理是根据已测量数据的空间位置和相关程度的不同，将不同的权赋给每个数据，并进行滑动加权平均，从而估计未测量区域的数据。其基本假设建立在空间相关先验模型上，要求空间数据（区域化变量）满足二阶平稳假设或本征假设。下面介绍普通Kriging插值方法的基本步骤：

3.1 计算半方差

3.2 绘制半方差图

在半方差图中，横轴表示距离，纵轴表示半方差。图中有三个参数：nugget、sill和range。其中，nugget是块金值，表示距离为零时的半方差；sill是基台，表示基本达到稳定时的半方差；range是变程，在变程内数据具有相关性（即半方差随距离增加而增大），变程外的数据之间互不相关（即半方差趋于恒定）。

3.3 选择模型并求得相应参数

做出半方差曲线后需要寻找与之拟合最好的理论变异函数模型，常用的模型有高斯模型、球状模型、线性模型和指数模型等。

4 两种插值方法在实际应用中的比较

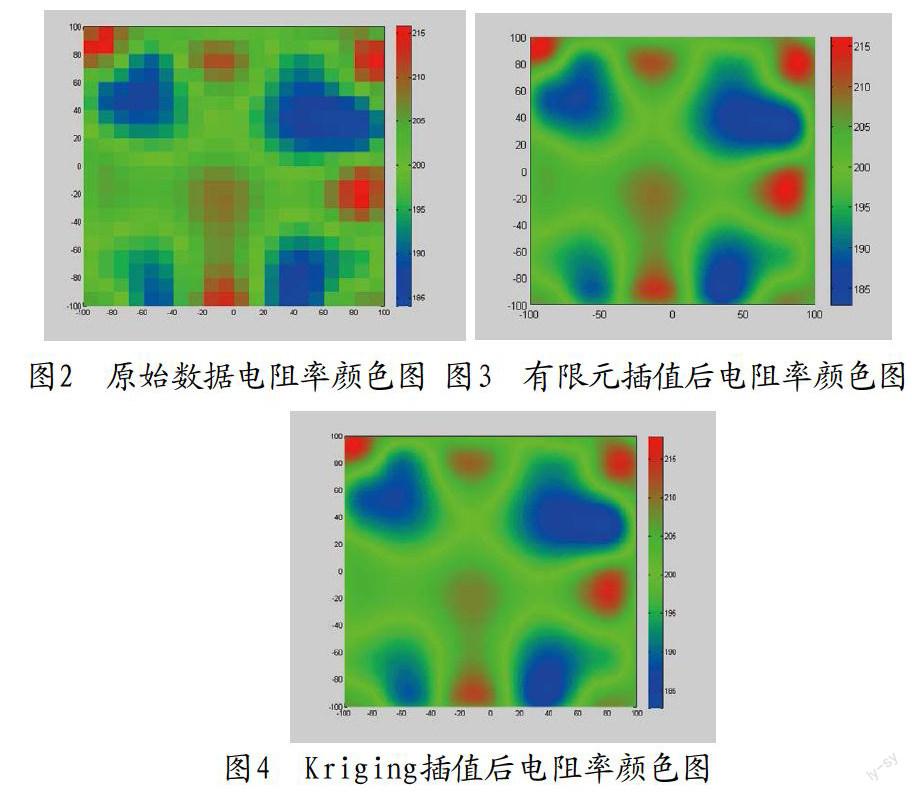
以空间中某三维体电阻率数据为例，通过插值将数据加密10倍。在MATLAB中编程，使用有限元插值和Kriging插值建立其数学模型。为了直观地比对插值后的效果，采用不同的颜色来表示电阻率的大小，并做出某一截面电阻率的颜色图。

数据与原始数据的颜色图，可以明显看出，插值后电阻率数据三维成像结果与插值前的电阻率数据三维成像结果形态基本一致，只是前者像素更高，颜色变化也更加平滑。Kriging插值后的平均值更接近于原始数据，而有限元插值后的标准差要小于Kriging插值。采用有限元插值得到的图像比Kriging算法得到的图像更平滑。

5 两种算法复杂性和计算量评估

5.1 算法复杂性概述

所谓算法复杂性是指算法运行时所需的计算机资源的量，其中所需的时间资源称为时间复杂性，需要的存储器资源称为空间复杂性。这些所需的资源的量集中反映了算法所采用方法的效率，与运行该算法的计算机无关。也就是说，所需的资源的量只依赖于算法本身的函数、算法要解决问题的规模和算法的输入输出。

5.2 算法复杂度和计算量评估

从空间复杂性上讲，Kriging算法含有大量矩阵运算，而有限元插值中的数据都是实数，显然Kriging算法运行时需要更多的存储空间，具有更高的空间复杂性。从时间复杂性上讲，Kriging算法含有大量矩阵运算，而有限元插值只是进行最基本的四则运算，显然Kriging算法具有更大的计算量，即更高的时间复杂性。

综上，Kriging算法具有更高的复杂度和计算量。

6 结语

第一，在实际问题中，通常需要许多位置的数据来解决必要的问题，但是由于技术与测量成本等原因，我们只能等间隔地选取部分点进行测量或选取容易测量的部分进行测量，因此必须对空间数据进行插值。本文以对三维体电阻率插值问题求解为例，建立的两种空间数据的插值模型，就是很好的两种算法，这两个模型具有重要的实际意义。

第二，从平均值这一指标来看，Kriging插值效果更好。从标准差这一指标来看，有限元插值效果更好。采用有限元插值得到的图像比Kriging算法得到的图像更平滑。考虑到计算量和复杂度，有限元插值算法不仅相对简单，而且效果不错。此外，我们在建立模型的过程中用到的分析问题、解决问题的方法，对其他工程问题及数学模型仍可使用。

第三，本文中有限元插值采用8节点的六面体作为基本单元，实际上还有9节点和20节点的六面体单元和四面体单元等一系列基本单元可供选用，有限元方法还有很大的潜力。

第四，本文中采用的是普通Kriging插值，实际上针对不同的情况，还有泛Kriging、协同Kriging、贝叶斯Kriging和指示Kriging等多种变化，以更好地处理各类具体问题。

第五，有限元方法最早应用于力学分析，在静电场和电磁场的插值中也有应用，其核心思想可以推广到一般连续介质的空间插值问题中，本文中用其对电阻率数据插值就是一个很好的例子。

第六，Kriging插值起源于地统计学，该方法不仅考虑待插点位置与已测量数据位置的相互关系，而且还考虑数据的空间相关性，在数学上提供了一种无偏最优估计的方法。该方法依赖于数学模型和统计模型，在空间数据处理上具有一定的普适性，可以推广到诸如气象分析等其他数据的插值中。

参考文献

[1]张雨霆.三维空间离散点数据场的插值方法[J].武汉大学学报（工学版），2008，41（4）.

[2]王德玲，李春光，葛修润.三维有限元位移场插值问题的研究和应用[J].岩土力学，2004，25（2）.

[3]田红.含复杂插值曲面实体六面体网格优化方法[J].计算机工程与设计，2009，30（2）.

[4]李新，程国栋，卢玲.空间内插方法比较[J].地球科学进展，2000，15（3）.

[5]靳国栋，刘衍聪，牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报，2003，24（3）.

[6]吴健生.三维可视化环境下矿体空间数据插值[J].北京大学学报（自然科学版），2004，40（4）.

作者简介：陈泽淇（1993-），男，陕西西安人，西北工业大学自动化学院学生，研究方向：自动化。

（责任编辑：陈 洁）