Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead
GONG Chao-an, CHEN Zhi-gang, YIN Li-kui
(National Defense Key Laboratory of Underground Damage Technology, North University of China, Taiyuan 030051, China)
龚超安, 陈智刚, 印立魁
(中北大学 地下目标毁伤技术国防重点学科实验室, 山西 太原 030051)
Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead
GONG Chao-an, CHEN Zhi-gang, YIN Li-kui
(NationalDefenseKeyLaboratoryofUndergroundDamageTechnology,NorthUniversityofChina,Taiyuan030051,China)
By studying shock wave propagation and fragment movement after the explosion of a blast fragmentation warhead, a whole calculation process about the place where fragments meet shock wave was proposed. A computing system for movement laws of fragments and shock wave was developed based on VC++. Numerical segment integration method is used for the calculation of shock wave velocity and displacement, which makes the calculation be more convenient. The movement of preformed fragments and shock wave was simulated by ANSYS/LS-DYNA. The results show that the simulation is nearly equal to calculation.
fragment; shock wave; LS-DYNA; VC++
0 Introduction
Blast fragmentation warhead mainly as anti-missile warhead has been researched a long time. Blast warhead mainly has three target damage effects: direct effect of products, damage effect of shock wave and kill effect of fragments. As two target damage ways, shock wave and fragment has different action principles therefore action order affects the effectiveness of damage[1-3]. The Third Research Institute of General Staff Corps of Engineers has fitted the distances with different ratios, load coefficient with the time during which fragment meets shock wave according to experiment data[4-7]. Therefore, study on the position where fragment meets shock wave is extremely important.
1 Calculation of TNT equivalence
1.1 Transformation from shelled charge to uncovered charge
When shelled explosive explodes, according to energy conservation law, the whole energy is transformed to the kinetic energy (KE) and internal energy (IE) of explosion products and the kinetic energy of the fragments, that is[8]
(1)
whereE1is the IE of explosion products;E2is the KE of explosion products;E3is the KE of fragments; andQvis explosion heat. The IE of explosion products is expresed as
wherer0is initial radius of the shell;ris expansion radius;γis polytropic exponent and equal to 3; andbis shape factor and equal to 2 for cylinder shell.
The KE of explosion products is expressed as
wherev0is the expansion velocity of shell;ais shape factor and equal to 2 for cylinder shell.

Thewholeenergyofexplosionproductsis
E1+E2=mQv-E3=mbeQv.
Theshelledchargecanbetransformedtouncoveredchargeby
(2)
whereβis load coefficient,β=m/M.
1.2 Transformation from other charges to TNT sphere charge
To transform other charges to spherical TNT charge, supposing that the explosion heat of explosive isQviand the mass ismbe, the transformation is done by
(3)
whereQvTis the explosion heat of TNT. Almost all of blast warheads are cylinders, therefore it can be calculated approximately as spherical charge when the propagation distance of shock wave is farther than the length of charge.
2 Calculation for velocity of shock wave
2.1 Calculation for overpressure of TNT
For the uncovered spherical TNT charge explosion in the infinite air, according to the specifications for design of national defense engineering in China[8], positive overpressure peak is calculated by
(4)
2.2 Relationship between overpressure and velocity of shock wave
The Rankine-Hugoniot formula shows the relationship between overpressure and velocity of shock wave[9], that is
(5)
(6)

(7)
Calculating the integral of reciprocal of Eq.(6), the relationship betweentandris got by
(8)
Due to the complexity of analytic solution for Eq.(8), Eq.(8) is converted into numerical integration in experimental calculation. After getting the step, a series of integral points are got and then they are drawn in the axis. The density of points shows the accuracy directly.
3 Calculation of fragment velocity and its decline
3.1 Calculation of fragment velocity
The Gurney formula is deduced according to energy conservation law[10], that is
(9)
(10)
3.2 Description for velocity decline of fragment
The formula for fragment velocity decline is[11]
(11)

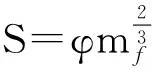
Table1Modificationfactorandattenuationcoefficientofinitialvelocity

KindsoffragmentsKH(m-1kg12)Naturalfragment1320PreformedfragmentsSphere0.7548Cylinder0.8416Cube0.9399Sector0.9363Half-preformedfragment0.95320
Calculating the integral of reciprocal of Eq.(11), the relationship betweentandLcan be got by
(12)
4 Determination of the place where fragment meets shock wave
For computing the displacementR, lett=T, the expression of the place and time of fragment can be got first according to initial velocity and velocity dedine. But there is not an analytic solution for Eq.(8). What is worse, the integral calculation is complex. In view of the theories and convenience, the author developed the computing systems for fragments and shock wave movement by using Visual C++. For Eq.(12), the system drew the curve in the coordinate system. For Eq.(8), the system used trapz function to compute numerical integration. After that, the point set was got and drawn in the coordinate system. MFC controls the data processing while TeeChart controls the drawing. The system shows the movement of fragment and shock wave directly. What’s more, it shows the distance between fragments and shock wave at any time. The framework of the system is shown in Fig.1.
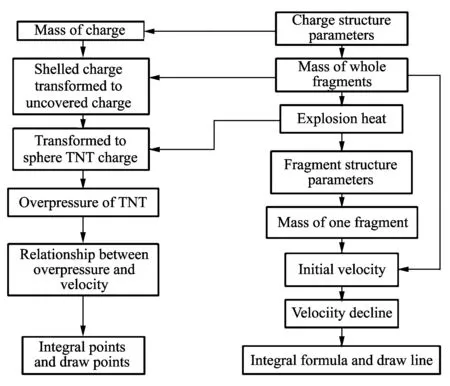
Fig.1 Framework of computing system of fragments and shock wave’s movement
5 Comparison of calculation and numerical simulation
For the preformed steel rectangle fragment warhead, the radius of TNT cylinder charge is 4.8 cm, and the height is 50 cm. There are 42 fragments one layer in radial direction, and 22 layers in axial direction. There are 924 preformed fragments in all. Each fragment’s mass is 0.04 kg. The whole mass of fragments is 37 kg.
5.1 Calculation
These parameters are input to the computing system, as shown in Fig.2.The curves are drawn, as shown in Fig.3. After explosion, there are two stages of movement[12]. The first stage: the velocity of shock wave is faster than that of fragment, and shock wave is further than fragment. The second stage: the velocity decline is more than shock wave decline, and fragment meets shock wave. After that, fragment is further than shock wave. The system shows that fragment meets shock wave at 7.1 ms while the displacement is 4.73 m.

Fig.2 Interface of inputting parameters
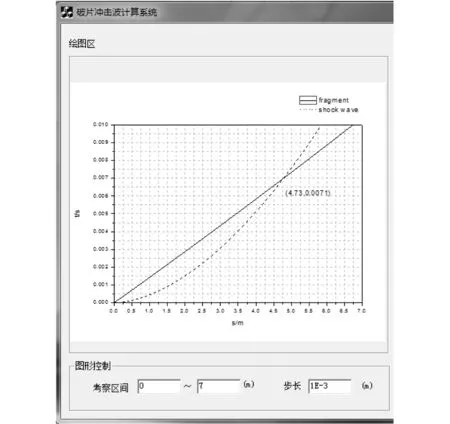
Fig.3 Curves of time-displacement for fragment and shock wave
5.2 Numerical simulation
The numerical simulation is performed by using ANSYS/LS-DYNA. Because of structural symmetry, 1/4 model is created to make calculation easy. Both charge and air are arbitrary Lagrange-Eular elements (ALE) while fragments are Lagrange elements. Liquid-solid coupling is used between ALE elements and Lagrange elements. The radius of air is 7 m. The pressure of air shows shock wave. The density of TNT charge is 1.59 g/cm2, and its constitution relationship is described by MAT_HIGH_EXPLOSIVE_BURN. Its state equation is JWL. The detonation way is point detonation. The density of fragment is 7.83 g/cm2, and its constitution relationship is Johnson-Cook. Its state equation is Gruneisen. The finite element model of warhead is shown in Fig.4. Fig.5 is the nephogram of air pressure and the small cubic blocks are preformed fragments. Fragments meet shock wave at 7 ms while the displacement is 4.69 m.

Fig.4 Finite element model of warhead

Fig.5 Nephogram of air pressure
It can be seem from Table 2 that the simulation is nearly equal to calculation.
Table 2 Comparison of displacement where fragment meets shock wave

FragmentkindDisplacement(m)CalculationSimulationSteelcube4.734.69
6 Conclusion
The whole calculation process is based on theories, therefore it is helpful to applicable for all structures. The system shows the distance between fragment and shock wave at any time. The characteristics of the two stages are reflected in the picture. It is more accurately control the order and the distance between shock wave and fragment.
[1] DONG Qiu-yang. Damage research of wing skins under projectile and shock wave. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013: 13-16.
[2] REN Dan-ping. Multiplex damages that the shock wave and the fragments do to the cruise missile. Nanjing: Nanjing Institute of Technology, 2006: 22-31.
[3] AN Zheng-tao, WANG Chao, ZHENG Jian-wei, et al. Theoretical research on action law of fragment and shock wave of traditional ammunition explosion. Blasting, 2012, 29(1): 1-4.
[4] LIU Gang, LI Xiang-dong, ZHANG Yuan. Numerical simulation of combined damage of fragments and shock wave on helicopter rotor. Computer Simulation, 2013, 30(6): 1-5.
[5] GUO Miao, YUAN Jun-ming, Liu Yu-cun, et al. Simulation of composite for phased array radome by fragments and shock wave. Blasting, 2014, 31(1): 1-5.
[6] OUYANG Chang-ming, DUAN Zhou-ping, SUN Bao-ping, et al. Experimental study on initiation of charge under combined shock wave and fragment impact. Explosion and Shock, 2013, 28(3): 1-4.
[7] LIU Sui-jiang. Analysis and numerical simulation for the protective performance of laminated shellproof board. Wuhan: Wuhan University of Science and Technology, 2007: 41-43.
[8] SUI Shu-yuan, WANG Shu-shan. Terminal effect study.Beijing: National Defense Industry Press, 2000: 290-292.
[9] ZHANG Bao-pi, ZHANG Qing-ming. Detonation physics. Beijing: Ordnance Industry Press, 2006: 52-60.
[10] Starks M W. Vulnerability science, a response to a criticism of the ballistic research haboratoey’s vulnerability modeling strategy, AD-A224785, 1990: 1-24.
[11] ZENG Shou-yi, JIANG Zhi-gang, CHEN Bing, et al. Discussion on the together effect of shock wave and fragment. In: Proceedings of the 9th Learning Annual Thesis Collection on Defense Engineering Branch of the Chinese Construction Engineering Academy, 2004: 1-4.
[12] LIANG Wei-ming, ZHANG Xiao-zhong, LIANG Shi-fa, et al. Experimental research on motion law of fragment and shock wave under the condition of internal explosion. Acta Armamentarii, 2009, 30(S2): 223-227.
某杀爆战斗部破片与冲击波运动规律研究
通过对某杀爆战斗部爆炸后破片运动及冲击波传播的研究, 理论推导了破片与冲击波相遇位置的求解全过程。 采用Visual C++开发破片与冲击波运动规律计算系统, 并用数值积分方法对冲击波速度与位移进行分段积分。 通过该系统计算了某预制破片战斗部破片与冲击波的相遇位置, 并运用ANSYS/LS-DYN数值模拟了该预制破片战斗部爆炸后破片与冲击波的运动, 数值模拟结果与计算结果基本相符。
破片; 冲击波; LS-DYNA; VC++
GONG Chao-an, CHEN Zhi-gang, YIN Li-kui. Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead. Journal of Measurement Science and Instrumentation, 2015, 6(3): 218-222. [
龚超安, 陈智刚, 印立魁
(中北大学 地下目标毁伤技术国防重点学科实验室, 山西 太原 030051)
10.3969/j.issn.1674-8042.2015.03.003]
GONG Chao-an (gca_bm@sina.com)
1674-8042(2015)03-0218-05 doi: 10.3969/j.issn.1674-8042.2015.03.003
Received date: 2015-05-05
CLD number: TJ410.3+3 Document code: A
——生态学
 Journal of Measurement Science and Instrumentation2015年3期
Journal of Measurement Science and Instrumentation2015年3期
- Journal of Measurement Science and Instrumentation的其它文章
- Numerical simulation of two-phase flow field in underwater sealing device based on dynamic mesh
- Ballistic impact simulation of Kevlar-129 fiber reinforced composite material
- Design of IRIG-B(AC) encoder based on FPGA
- X-ray image distortion correction based on SVR
- Application of adaptive Kalman filter in rocket impact point estimation
- Simulation of small-aperture deep hole drilling based on ABAQUS
