A fuzzy immune algorithm and its application in solvent tower soft sensor modeling

MENG Ke, DONG Zhao-yang, GAO Xiao-dan, WANG Hai-ming, LI Xiao

(1. Centre for Intelligent Electricity Networks, The University of Newcastle, Callaghan 2308, Australia;2. School of Electrical and Information Engineering, The University of Sydney, Sydney 2006, Australia;3. School of Computer Science and Control Engineering, North University of China, Taiyuan 030051, China)



A fuzzy immune algorithm and its application in solvent tower soft sensor modeling

MENG Ke1,2, DONG Zhao-yang2, GAO Xiao-dan1, WANG Hai-ming1, LI Xiao3

(1.CentreforIntelligentElectricityNetworks,TheUniversityofNewcastle,Callaghan2308,Australia;2.SchoolofElectricalandInformationEngineering,TheUniversityofSydney,Sydney2006,Australia;3.SchoolofComputerScienceandControlEngineering,NorthUniversityofChina,Taiyuan030051,China)

An improved immune algorithm is proposed in this paper. The problems, such as convergence speed and optimization precision, existing in the basic immune algorithm are well addressed. Besides, a fuzzy adaptive method is presented by using the fuzzy system to realize the adaptive selection of two key parameters (possibility of crossover and mutation). By comparing and analyzing the results of several benchmark functions, the performance of fuzzy immune algorithm (FIA) is approved. Not only the difficulty of parameters selection is relieved, but also the precision and stability are improved. At last, the FIA is applied to optimization of the structure and parameters in radial basis function neural network (RBFNN) based on an orthogonal sequential method. And the availability of algorithm is proved by applying RBFNN in modeling in soft sensor of solvent tower.

immune algorithm; fuzzy system; radial basis function neural network (RBFNN); soft sensor

0 Introduction

With the development of immunology and its research methods, the mechanism of biologic immune system has attracted increasing attention from researchers in recent years. Due to the powerful ability of information processing and special characteristics such as diversity, adaptive trait, biologic immune system has become a hot spot of artificial intelligence.

Being the defense system of mammal, immune system plays a significant role in keeping the normal life activities of animals. If it is weakened or destroyed, lives will be endangered. The process that immune system annihilates viruses can be briefly described as follows:

Once bacteria invade and enter the bloodstream or lymphatic system, they will encounter B cell and the antibodies withheld within B cell’s membrane will detect antigens in the bacteria. Thenceforth, T cells communicate with B cells based on the received information about the antigen from macrophages earlier and by so doing, B cells are inspired to propagate. The propagated B cells are converted into memory cells and antibodies are produced. With the aid of macrophages and other proteins within biologic bodies, antibodies bind to antigens and kill the antigens after they enter into blood system through the heart.

Being an innovative optimization algorithm based on immune mechanism, the immune algorithm (IA)[1]is employed to address the multi-modal function optimization problem. It imitating the principle of our defense system annihilating foreign disease-causing bacteria or viruses through self-learning and self-adjusting. The capability of somatic theory and network hypothesis of immune system of multi-modal optimization problems has been examined in Ref.[2]. An IA is introduced in Ref.[3] to search for diverse solutions to design problems for electromagnetic devices, where optimal solutions are aggregated in memory cells.

Differences in the production system for memory and antibodies distinguish IA from genetic algorithm (GA) although they are quite similar. Besides, IA manipulates a population of candidates simultaneously in the search space whereas GA manipulates just one. Compared with GA and other evolution programming, IA promotes the general search ability through the mechanism based on memory pool. At the same time, it realizes the function of self-adjusting by calculating affinity and concentration. To some extent, it avoids premature convergence.

1 Soft sensor and RBF neural network

In order to get eligible production, quality control wields an important role in industrial manufacture. Because of the complexity of industrial process especially in the petrochemical industry, it is very difficult to realize the real-time strict control of the quality of some products. Under many circumstances, the qualities of many products are tested off-line by labor because of the high price, difficulty of maintenance, time latency of on-line measure meters.

The conception of soft sensors, which combines control knowledge and technologic theories together, was firstly brought forward in Ref.[4]. Some variables which can be easily measured are selected to compute real-time reliable estimates data of other ones which can not or is difficult to be measured by designing proper algorithms. Nonlinear modeling techniques are usually utilized to develop soft sensors to handle the peculiar nonlinearities of processes[4]. Not only can soft sensors be operated alone as a valuable, economic replacement of costly hardware sensors, but also work in parallel with real sensors to allow model-based techniques to be adopted in order to develop fault detection functions devoted to the analysis of the sensor’s health status.

Radial basis function neural networks (RBFNN) is an excellent neural network in performance. In 1990, Girosi and Poggio had proved RBFNN can approach any nonlinear functions by discretionary precision[5]. RBF networks are gaining increasing popularity in many scientific and engineering fields as a result of their strengths compared with other types of artificial neural networks (ANN), e.g. improved approximation capabilities, simpler network structures and faster learning algorithms.

RBF networks are composed of three layers, including the input, hidden and output layers, which form an unique neural network architecture. The input layer communicates the entire network to its outside environment. In the hidden layer, all the nodes are connected with centers, and they are vectors with a dimension identical to the number of inputs to the network. A RBF is employed to pass the node activity; the feedback from a hidden node is generated. Lastly, the output serves as a summation unit, which is linear. The structure of a typical RBFNN is presented in Fig.1.

Fig.1 Typical MISO RBFNN

But how to decide the number of neurons within the hidden layer has always been the problem counteracting the application of RBFNN. There is a possibility that a small network never converges, however, a large network converges fast but lacks the generalization ability. Besides a suitable network size, there are many other questions that need to be answered to use a network for a particular problem. Learning step, proper training procedure, number of layers, network initialization, value of gain and the number of neurons in each layer are some difficulties which block the wide application of neural network. In this paper an orthogonal sequential method[6]is represented producing RBFNN models based on an improved IA, which is used to auto-configure the structure of the network and obtain the model parameters.

2 Fuzzy immune algorithm

2.1 Basic principles of immune algorithm

For the optimization problem, the antigens and antibodies in the immune system are represented as the objective functions and feasible solutions, respectively.

The coding method for traditional IA is similar to that for the GA, which is coded in binary. In this paper a new real-coding based evolution IA because of the advantages of real coding algorithm in training neural network[7]is represented, which effectively improves the performance of traditional IA, solving the problems such as premature convergence, low speed of calculation and low precision.

2.2 Calculation strategy of FIA

The steps of FIA are illustrated as shown in Fig.2.

Fig.2 Flow chart of FIA

Step 1 (Recognize antigen)

Antigen: objective function (generally minimum value).

Antibody: feasible solutions.

Step 2 (Produce initial antibody population and memory pool)

In this step, the antibodies are generated randomly and then compartmentalized to the given intervals. The memory pool is a zero matrix of given size.

Step 3 (Calculate the affinity values of all antibodies)

IA uses affinity value as a discriminator of the quality of solutions represented by the antibodies in a population. Because the final target of the algorithm is searching the minimum value, function values of all the antibodies are calculated and sorted in ascending sequence.

To calculate the affinity valueaffinity(i) of antibodyi, it is given by

(1)

whereris a random number in the interval [0.01,0.3].

Step 4 (Update memory pool)

Eminent antibodies from the present population are selected by their affinity values and concentrations in order to update memory pool which can be used to generate the offspring antibodies population.

Step 5 (Select antibodies)

1) To calculate the concentrationcon(i) of antibodyi, it is given by

(2)

where

(3)

2) To calculate the selection probabilityPs(i) of antibodyi, it is given by

(4)

3) A roulette selection is implemented based on the computed selection probability for the antibodies. This allocates each antibody a probability of being selected proportional to its relative affinity and concentration. A new antibody generation can therefore be formed by spinning the designed roulette.

Step 6 (Determine crossover and mutation rates through fuzzy method)

In IA, many parameters play an important role in determining convergence and convergent rate, such as crossover and mutation rates. Crossover is one key IA operator that promotes the new region exploration ability in the search space. Generally, crossover rate should be chosen comparatively big[8], between 0.7 and 1.0. Mutation is another IA operator which guarantees the diversity of the population. In Ref. [8], the mutation rate should be chosen between thousandths and hundredths.

According to Ref.[9], statistical method, support vector machine or neural network can be utilized to adjust crossover and mutation rates. However, we have found that fuzzy system approach makes better contributions to the IA in both time consumption and precision when compared with above methodologies.

Themembershipfunctionsforinputfd(t),andoutputΔPcareshowninFigs.3-6.Inthesamewaythemembershipfunctionsforinputfd(t), Pm,ΔPmandfuzzydecisiontableforΔPmcanbedrawn.

Fig.3 Membership function of fd(t)

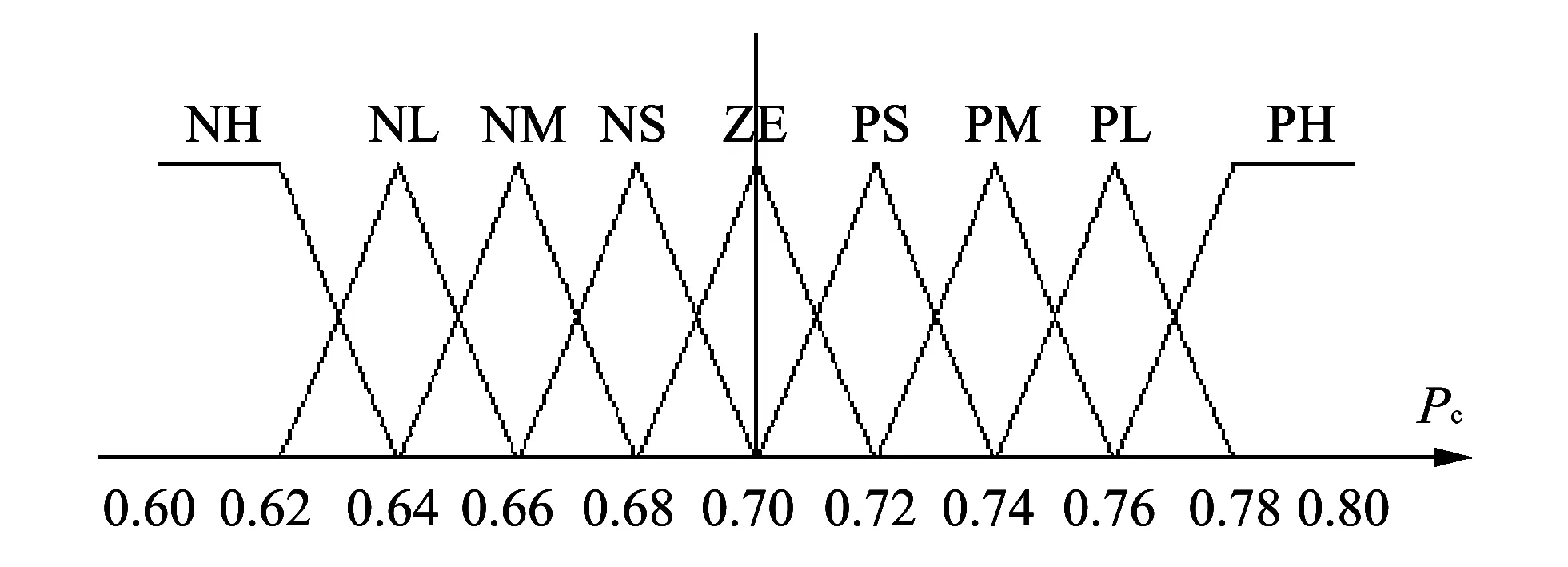
Fig.4 Membership function of Pc

Fig.5 Membership function of ΔPc

Fig.6 Membership function of ΔPm

According to a great deal of experimental data and expert knowledge, the fuzzy decision for ΔPcis made and presented in Table 1. By virtue of the same theory, the fuzzy decision table for ΔPmcan be generated. In the table, NH, NL, NM, NS, ZE, PS, PM, PL and PH are abbreviated for Negative Huge, Negative Large, Negative Medium, Negative Small, Zero, Positive Small, Positive Medium, Positive Large and Positive Huge, respectively.

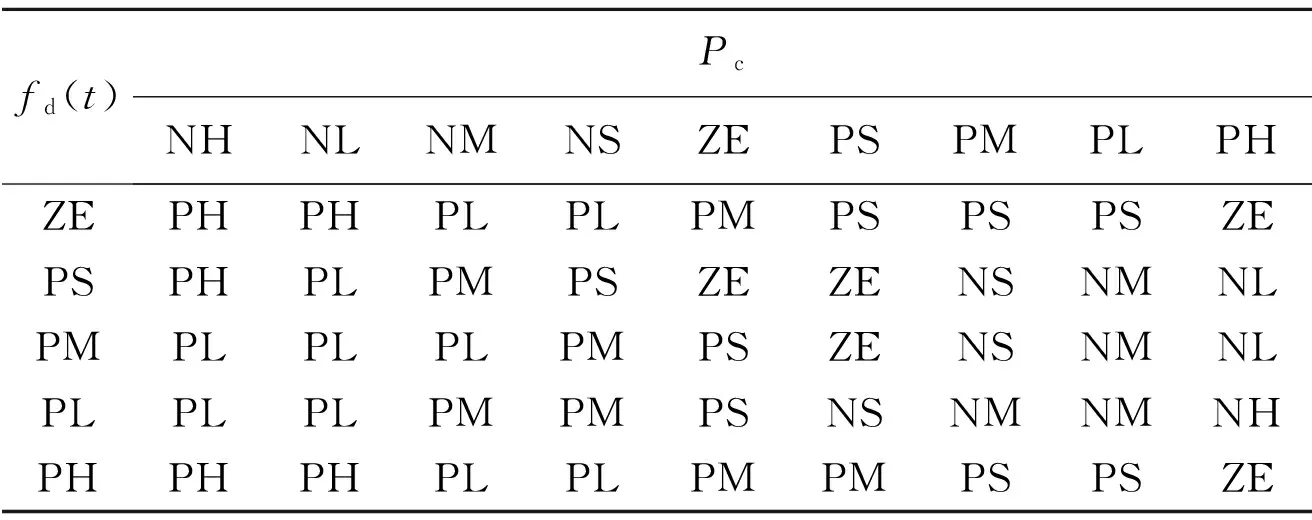
Table 1 Fuzzy decision table for ΔPc

Step 7 (Crossover implementation)

The crossover operator represents the mixing of antibiotic material from two selected parent antibodies to produce one or two child offspring antibody population. The amount of antibodies take part in crossover implementation is determined by crossover ratePc, which is adjusted by fuzzy method.

An improved arithmetic crossover operator is described as

(5)

whereb1=0.5+b,b2=0.5-b, andbis a random number in interval [0,1].

If the offspring antibody exceeds the given intervals, another operator will be selected.

(6)

Step 8 (Mutation implementation)

An uneven mutation method[10-11]is described as follows:

For one given parent antibody, if its elementxmis randomly selected to mutation, the corresponding element in its offspring is likely to change in two possibilities

(7)

(8)

whereTis maximum generation;tis current generation;ris a fixed uneven parameter, usuallyr=2;bis a random number in the interval [0,1].

In this paper, an improved mutation method is introduced, and its idea mainly comes from differential algorithm[12].

(9)

whereantibodybestis the optimal antibody of the current generation which is stored in memory pool.

Step 9 (Generate new antibody population and update memory pool)

Antibodies with high affinity value will evolve into next generation and be added into memory pool. Given number of new antibodies will be added into antibody population replacing antibodies with low affinity value.

Step 10 (Termination criterion).

For this step, the search is terminated if the following conditions are satisfied:

1) The values for minvaluedo not change for several generations.

2) When the set number of evolutionTis achieved.

2.3 Test examples

Several standard test functions are used to examine the ability of FIA and its advantages superior to other algorithms in the same test environment and condition. Except for parameters adaptive selection, the FIA is similar to other algorithms in flow and thought. The standard test functions and test results are shown in Table 2 and Table 3, respectively.

Table 2 Three standard test functions

Table 3 Results of test functions

The above data indicate that FIA can effectively solve the premature problem and is suitable for complex optimization problems. The algorithm is not trapped by the local optimal solution and can promptly and accurately obtain a full set of global optimal solutions, which are incomparable in other similar algorithms.

3 Configuration of RBFNN using FIA

Like GA and other evolution algorithms[7,13], IA has three main applications in neural network:

1) The parameters learning of neural network;

2) The topology structure selection of neural network;

3) The parameters and structure optimization of neural network.

And the standard procedure for RBF networks learning problem can be decomposed into two steps: The first one is obtaining the number and centers of the nodes in hidden layer and the second one is calculation of the connection weights using simple linear regression.

3.1 General ideas and theories[6]

For typical RBFNN, ifwidenotes output weights, φi(X,Ci)denotestheoutputofithneuron, X=[x1,x2,…,xm]isinputvector, Cidenotesthehiddennodecenterlocationsofithneuronandydenoteslinearsummationofoutputofhiddenlayerneurons.IftheRBFisGaussfunction,

(10)

(11)

Foronesetoftrainingdata,theequationcanbetransformedinto

(12)

Andthen

(13)

(14)

(15)

Sothegivenequationscanbetransformedinto

(16)

(17)

(18)

3.2 Two-step learning strategy of RBFNN

3.2.1 Design of network structure

Real-coded algorithm is suitable for neural network training because the antibodies are the real values in neural network. The real-coded method forithantibody is that the formern+1 columns are relevantncenters and one warp and the last column is affinity value of the antibody.

The steps of RBFNN training are depicted as:

Step 1: Initialization.i=1, E0=Y.

Step 3: If output satisfies stopping criterion, network training will stop. Otherwise,i=i+1, and another neuron will be added.

3.2.2 Design of network output layer

Because of the output layer is linear and it serves as a summation unit, the least square method can be chosen to calculate

(19)

3.3 Result of soft sensor

One pure-terephthalic acid (PTA) solvent tower is chosen as research object in this paper and the ultimately target is to establish the soft sensor model for acid content of the bottom flow of the solvent tower. Solvent dehydration is an important unit in PTA manufacture process. Because of the long delay and slow dynamic response of the rectify process, it is very difficult to realize the real-time control of the production quality. The running situation of the control system largely depends on the operators’ technical levels and habits. Although the set can run smoothly in a short time, it cannot reach the optimal state. Great care was taken in both selecting the appropriate set of training examples, which covered all the operating conditions of the plant. According to technologic flow, three parameters (conductance, temperature and pressure) are selected as inputs to the RBF neural network, whereas the output is the relevant acid content. For 175 metrical data, former 100 are chosen to train neural network and the other 75 are used to determine the availability and generalization ability of the neural network.

To avoid over-learning phenomena, an early stopping approach is used. The parameters in FIA are set as

Popsize=50, Memorypool=20,

And the results of training and estimation are shown in Figs.7 and 8. Parameters comparison between different neural netowkrs are presented in Table 4.

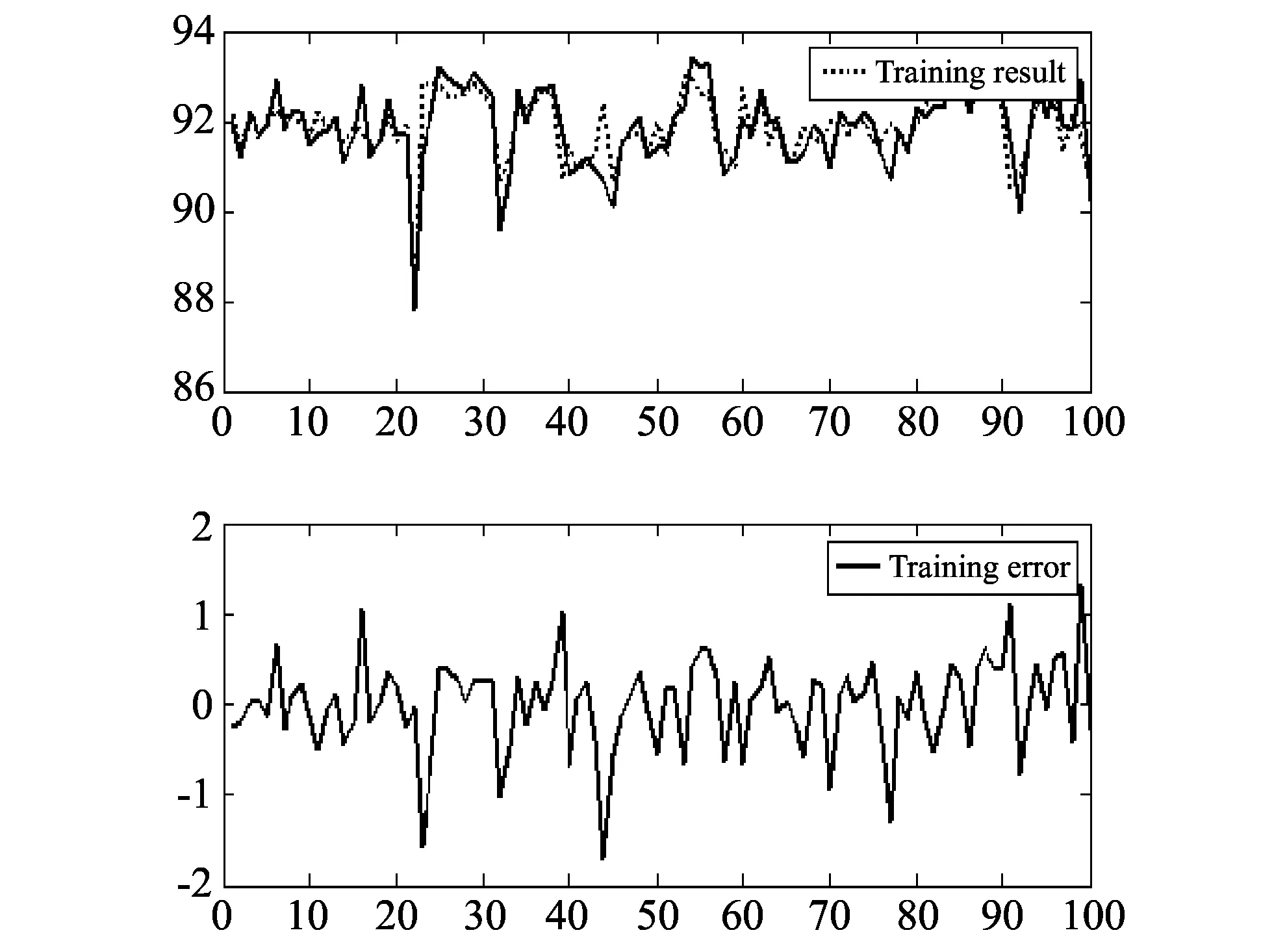
Fig.7 RBFNN training result

Fig.8 Comparison between NN estimation and corresponding actual data

Table 4 Parameters comparison between different neural networks

NetworksNumberofnodesinhiddenlayerMSEMaxrelativeerrorStandardrelativeerrorFIARBF80.11680.01870.0028OLSRBF90.13360.02240.0031ConventionalRBF120.14190.023540.0033

4 Conclusion

The simulation results indicate that the proposed methodology is effective and accurate. The parameters of neural network are optimized by using FIA, not only the number of nodes in hidden layer can be reduced, but also the generalization ability can be improved. As the study of combining FIA and RBFNN in soft sensor modeling is emerging recently, there are many aspects we can borrow from the immune system and fuzzy system, and further research is needed.

[1] Liao G C, Tsao T P. Application embedded chaos search immune genetic algorithm for short-term unit commitment. Electric Power Systems Research, 2004, 71(2)： 135-144.

[2] Fukuda T, Mori K, Tsukiyama M. Parallel search for multi-modal function optimization with diversity and learning of immune algorithm. Artificial Immune Systems and Their Applications, 1999： 210-220.

[3] Chun J S, Lim, J P, Jung H K, et al. Multisolution optimization of permanent magnet linear synchronous motor for high thrust and acceleration operation. In： Proceedings of International Conference on Electric Machines and Drives (IEMD 99), 1999: 57-59.

[4] Fortuna L, Rizzo A, Sinatra M, et al. Soft analyzers for a sulfur recovery unit. Control Engineering Practice, 2003, 11(12)： 1491-1500.

[5] Girosi F, Piggio T. Networks and the best approximation property. Biological Cybernetics, 1990, 63(3)： 169-179.

[6] BAO Zhi-jun, WANG Xian-lai. RBF neural networks based on orthogonal sequential genetic algorithm. In： Proceeding of the 22nd Chinese Control Conference, Yichang, China, 2003： 1.

[7] Michalewicz Z. Genetic algorithms + data structures=evolution program. New York: Springer Verlag, 1994.

[8] Braberman V A. Verification of real-time design： combining scheduling theory with automatic formal verficaton. Software Engineering Notes, 1999, 24(6)： 494-511.

[9] Shi Y, Eberhart R, Chen Y. Implementation of evolutionary fuzzy system. IEEE Transactions on Fuzzy System, 1999, 7(2)： 109-119.

[10] Thompson J M, Miller S P. Specification-based prototyping for embedded. Software Engineering Notes, 1999, 24(6)： 163-180.

[11] Fierz H. The CIP method： component- and model-based construction of embedded system. Software Engineering Notes, 1999, 24(6)： 375-393.

[12] Lopez-Cruz I L, van Willigenburg L G, van Straten G. Efficient differential evolution algorithms for multimodal optimal control problems. Applied Soft Computing, 2003, 3： 97-122.

[13] Goldberg D E. Genetic Algorithms in search, optimization and machine learning. MA： Addison-Wesley, 1989.

模糊免疫算法及其在溶剂脱水塔软测量建模中的应用

孟 科1， 2， 董朝阳2， 高晓丹1， 王海明1， 李 晓3

(1. Centre for Intelligent Electricity Networks, The University of Newcastle, Callaghan 2308, Australia;2. School of Electrical and Information Engineering, The University of Sydney, Sydney 2006, Australia;3. 中北大学 计算机与控制工程学院， 山西 太原 030051)

本文针对基本免疫算法收敛速度慢、 计算精度低等缺点， 提出了模糊免疫算法。 该算法引入模糊技术， 对关键参数(交叉概率和变异概率)实现了模糊自适应调整。 通过标准测试函数实验结果的对比， 其可行性和有效性得到证明， 不仅减轻了原始算法中参数确定存在的困难， 而且提高了算法的计算速度和精度。 其次， 本文将模糊免疫算法用于径向基神经网络的训练， 并将该神经网络应用于溶剂脱水塔软测量模型。 仿真实验证明， 模糊免疫算法优化的径向基函数神经网络具有良好的泛化性能。

免疫算法； 模糊系统； 径向基神经网络； 软测量

MENG Ke, DONG Zhao-yang, GAO Xiao-dan, et al. A fuzzy immune algorithm and its application in solvent tower soft sensor modeling. Journal of Measurement Science and Instrumentation, 2015, 6(2)： 197-204.

10.3969/j.issn.1674-8042.2015.02.016

MENG Ke (ke.meng@newcastle.edu.cn)

1674-8042(2015)02-0197-08 doi： 10.3969/j.issn.1674-8042.2015.02.016

Received date： 2015-02-25

CLD number： TP273+.4 Document code： A