h时标上带有限分布时滞的集群行为的动力学研究
肖 强,黄振坤
(集美大学理学院,福建 厦门 361021)

肖强,黄振坤
(集美大学理学院,福建 厦门 361021)
[摘要]研究了h时标上包含有限分布时滞的基于吸引/排斥函数的群聚模型.基于Lyapunov稳定性方法和时标理论,研究了集群的稳定性,证明了所有个体在有限时间会聚集到一个有限区域.最后,给出了一些模拟结果来验证结果的有效性.
[关键词]集群;时滞;聚集行为;h时标
0引言
近年来,有益于协作群聚行为和多个体集群行为的研究成为了一个热点[1-4].研究中基本的问题是如何根据个体之间的相互作用来建模和分析集群行为,很久以来生物学家们致力于理解和建立群聚模型[5-6].普遍的理解是集群行为是基于个体间长距离相互吸引和短距离相互排斥相互作用的结果[1].Gazi等研究了个体一阶连续运动模型[7],证明了所有个体在有限时间内会形成一个群聚体,并给出了群聚体一个显式的界.他们用的一般方法是将个体看做一个粒子并通过相互作用来研究集群行为[8].然而,由于个体间的交流存在时间延迟,使得系统表现出复杂的动力学行为,如发散性和稳定性等,因此将分布时滞考虑到模型中是很重要的.文献[9]考虑了基于同步分布控制方法的离散一维和二维群聚结构.文献[10]提出了在合适的环境中带有交流时滞的群聚模型,并且得到了稳定性结果.文献[11]描述了自治飞行器的编队控制策略.
群体中过去的行为对现在有着很大的影响,而且这种影响因其复杂性难以刻画,在一段时间内成为研究中一个难点.分布时滞能很好地刻画和量化这些时滞本质的影响,分布时滞不仅影响着群体最终群聚半径范围的大小,而且决定着群聚形成的时间.本文介绍了时标上时滞群聚模型,分析了合适条件下集群行为和群聚的动力学性质,并给出了群聚模型的一些模拟结果.
1预备知识
本节中,给出一些关于时标的基本概念和一些引理,它们均可以在文献[12]中找到.

定义1[12]令f:T→R,t∈Tk,则满足以下条件的fΔ,即对任意ε>0,存在t的邻域U,有:,∀s∈U,则称它为f在t处的Δ-导数.若fΔ(t)在所有t∈Tk均存在,则称f是Δ-可微的.
引理1[12]对任意给定的时标T和函数f(t),若f∈Crd且t∈Tk,则(t).
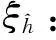
引理2[12]对任意给定的时标T和函数p(t),若p(t)∈R,那么ep(t,t0)是以下初值问题的唯一解:yΔ=p(t)y,y(t0)=1,t∈T,其中:T.
引理3[12]对任意给定的时标T,若函数y(t),f(t)∈Crd且p(t)∈R+.则对于所有的t∈T,yΔ(t)≤p(t)y(t)+f(t),蕴含着y(t)T.
2群聚模型
本节中考虑的是n维欧式空间中M个个体组成的群体,每个个体抽象成一个点.个体的运动是由以下在时标上带有有限分布时滞的微分方程控制:

(1)


3主要结论
假设1核函数满足:kij(t)=kji(t),∀t∈[0,hq0],∀i,j=1,2,…,M.
注2核函数实际上是一个权重函数,过去不同的时间与不同的位置对现在时刻有着不同的影响,核函数量化着这些影响.许多函数都可以成为核函数,例如k12(t)=e-t,k23(t)=1/t等.
为研究时滞群聚模型的稳定性,使用了文献[9]提供的稳定性概念.

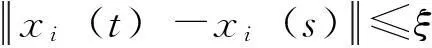


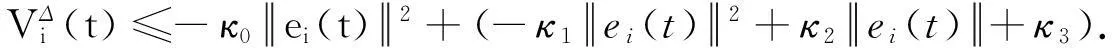
(2)

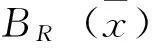

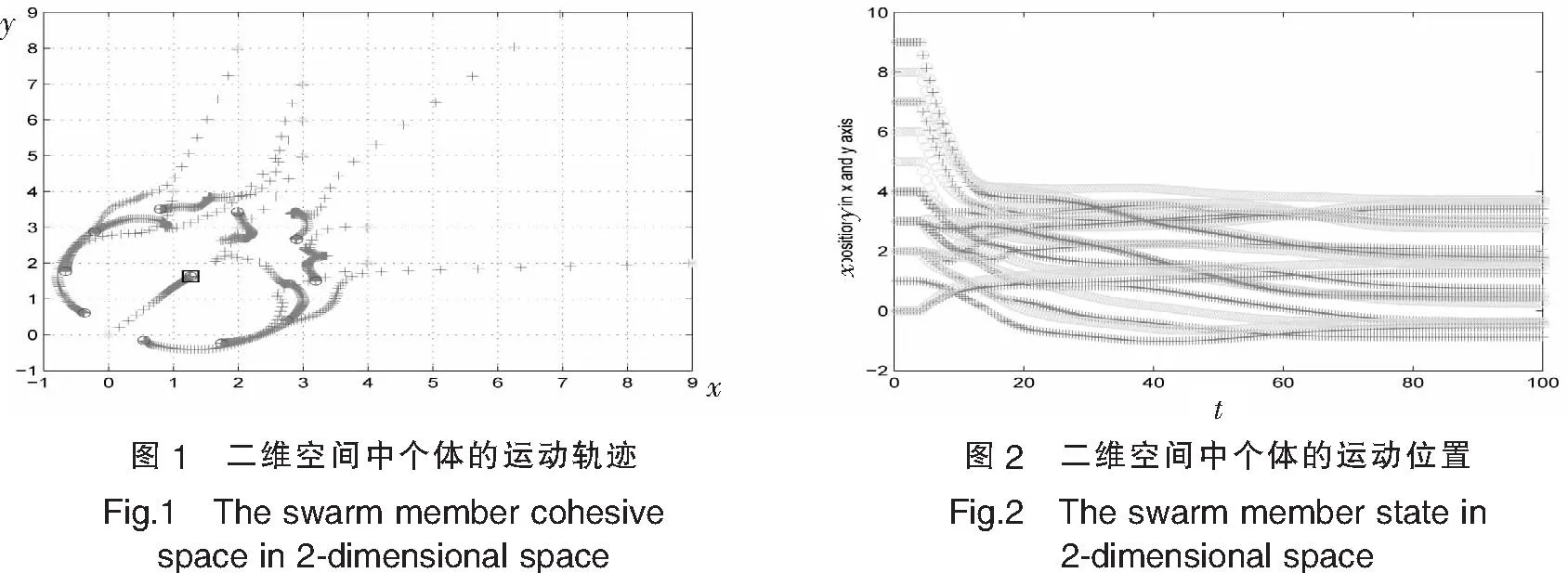
4数值模拟

[参考文献]
[1]GAZI V,PASSINO K M.Stability analysis of swarms[J].IEEE Trans Automat Contr,2003,48(4):692-697.
[2]CZIROKA,VICSEKT.Collectivebehaviosofinteractingselfpropelledparticles[J].JPhysA:MathNuclearGeneral,2000,281(1/4):17-29.
[3]BARTOSIEWICZZ,PIOTROWWSKAE,WYRWASM.Stability,stabilizationandobserversoflinearcontrolsystemsontimesacles[C]//2007 4thIEEEConferenceonDecisionandControl.Neworleans:IEEE,2007:2803-2808.
[4]GAZIV,PASSINOKM.Aclassofattraction/repulsionfunctionsforstableswarmaggregations[J].IEEEConferenceonDecisionandControl,2003,77(18):2842-2847.
[5]GAZIV,PASSINOKM.Stabilityanalysisofswarmsinanenvironmentwithanattractant/repelellentprofiles[J].ProceddingsoftheAmericanControlConference,2002,3:1819-1824.
[6]GAZIV,PASSINOKM.Stabilityanalysisofsocialforagingswarms:combinedeffectsofattractant/replellentprofiles[C]//IEEE.Proceedingsofthe41stIEEEConferenceonDecisionandControl.LasVegas:IEEE,2002:2848-2853.
[7]GAZIV,PASSINOKM.Stabilityofsocialforagingswarm[J].IEEETransSystManCybernetPartB:Cybernet,2004,34(1):539-557.
[8]GRUMBAUMD,OKUBOA.Modelingsocialanimalaggregations[J].FrontiersinTheoreticalBiology,1994,100:296-325.
[9]LIUQ,LIAOX,LIUY,etal.Dynamicsofaninertialtwo-neuronsystemwithtimedelay[J].NonlinearDyn,2009,58(3):573-609.
[10]LIUQ,WANGL,LIAOX.Stabilityanalysisofswarmswithinteractiontimedelays[J].InformationSciences,2012,192:244-254.
[11]GIULIETTIF,POLLINIL,INNOCENTIM.Autonomousformationflight[J].IEEETransRobotAutomat,2000,14:926-939.
[12]BOHNERM,PETERSONA.Dynamicequationsontimescales:anintroductionwithapplications[M].Boston:BirkhWauser,2001.
[13]GAZIV,PASSINOKM.Stabilityofaone-dimensionaldiscrete-timeasynchronousswarm[J].IEEETransSystManCybernetPartB:Cybernet,2005,35(4):834-841.
(责任编辑马建华英文审校黄振坤)

(School of Science,Jimei University,Xiamen 361021,China)
Abstract:In this paper,a swarm model based on attraction/repulsion functions with finite-distributed delays onhtime scale was investigated.The stability of the swarm based on Lyapunov stability method and theory of time scales was studied.It was shown that all the members of the swarm will eventually gather into a bounded region in finite time.In the end,simulation results were presented to illustrate the effectiveness of our results.
Key words:swarm;time delays;collective behavior;htime scale
[中图分类号]O 193
[文献标志码]A
[文章编号]1007-7405(2015)06-0470-05
[作者简介]肖强(1989—),男,硕士生,从事神经网络方面研究.通信作者:黄振坤(1977—),男,教授,硕导,从事神经网络方向研究,E-mail:hzk974226@jmu.edu.cn.
[基金项目]国家自然科学基金资助项目(61573005,11361010);福建省自然科学基金资助项目(2012J06001)
[收稿日期]2015-01-16[修回日期]2015-03-20

