车道被占用对道路通行能力的影响
邱家理,周雪刚,朱佳鹏,叶 云
(广东金融学院 应用数学系,广州 510521)
参 考 文 献
车道被占用对道路通行能力的影响
邱家理,周雪刚,朱佳鹏,叶 云
(广东金融学院 应用数学系,广州 510521)
通过对占用不同车道的车流量数据进行统计,分析了不同车道的实际通行能力变化过程,建立了交通流-密-速模型.并且通过建立微分方程模型,得到了受交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的函数关系.
道路通行能力;交通流-密-速模型;多元线性回归模型;数据拟合
0 导 论
改革开放以来,国内的汽车占有量日益增加,尤其是城市的汽车占有量,导致城市道路具有交通流密集、连续性大的特点,尽管是短暂的车道被占用也会降低路段所有的车道的通行能力,引起车辆排队交通阻塞.
如何解决车道被占用导致城市道路通行能力降低的问题日益成为城市交通规划的重要问题之一.通过对车道被占用导致道路通行能力的变化,以及对不同车道被占用所引起的道路通行能力差异的原因进行研究分析,有助于帮助交通部门采取相关措施,缓解车道被占用时道路通行能力的压力.
1 模型的建立、求解及结果分析
1.1 交通流- 密-速模型
在相关文献中,等效通行能力概念被定义为: 将一条由路段和交叉口组成的实际道路, 抽象成一条没有交叉口的等效路段;本文采用实际道路各路段流量的平均值,作为等效路段的断面流量.
本文根据一定的交通流- 密-速模型回归得到的等效路段的通行能力,定义为实际城市道路的等效通行能力.其中:实际道路的行程车速定义为等效车速, 记为v;实际道路指定路段单位长度内的车辆数定义为等效密度, 记为k;二者的乘积定义为等效流量q, 即得如下交通流-密-速模型:
q=k×v
(1)
1935年,格林希尔治通过对观测数据的统计分析,提出车速与密度之间的一线性模型:
(2)
其中vf是密度k=0时的车速,即理论上最高车速,称为自由流;kj是速度v=0时的密度,称为阻塞密度.
研究和经验表明,线性模型适合通常的车流密度适中的情况,则:密度较大时适用的对数模型:
(3)
密度较小时适用的指数模型:
(4)
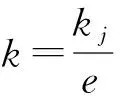
(5)

同理,由(1)(2)式可导出流量与车速的关系:
(6)
由(2)、(5)、(6)式确定的如图1所示.
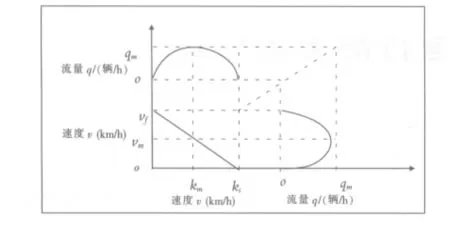
图1 理论交通流的流量、速度、密度关系图
注:qm是最大流量,km,vm分别对应最大流量的密度和速度
1.2 事故1所处横断面实际通行能力的变化过程
由于影响实际通行能力因素有:车道宽度、侧向净空、纵坡度、视距不足、沿途条件等,因此直接使用实际通行能力的公式,难以寻找相应的因素数据信息.由此,通过交通流-密-速模型回归得到的等效路段的通行能力[3].并且由于两车道被占用使交通阻塞,用事故横断面的通行能力表征城市道路单元的通行能力, 完全忽视其他非事故横断面的影响并不合理,在一定的情况下也是错误的[1].因此,采用交通流-密-速模型回归间接得到等效路段的通行能力.若实际的交通流-密-速模型的三者的关系与理论的交通流-密-速模型三者关系吻合,即可用交通流流量的变化对实际通行的变化进行描述、分析.

利用matlab工具箱对导入的事故1的数据进行绘图,其结果如图2所示.

图2 事故1交通流密度、速度、流量图
通过对所得数据进行拟合处理,得出实际的交通流密度、速度、流量图并检验三者所体现的关系是否符合理论的交通流密度、速度、流量关系,运行检验程序,结果表明:
(1)交通流速度与密度所拟合的结果,体现了两者之间呈反比例关系.
(2)交通流流量与密度所拟合的结果,显示出:交通流密度与交通流流量的函数图像呈倒U型.
(3)交通流流量与速度所拟合的结果,显示出:交通流速度与交通流流量的函数图像呈倒U型.
通过检验,图2呈现趋势表明:
(1)从0基准时刻(即事故发生)到事故撤离为止,交通流流量整体呈现出起伏交错的周期性变化.
(2)随着事故发生时间推移,不同的时间段呈现出不同波动规律:事故前期(即0~320 s时间段),流量的变化呈现较大的起伏波动规律;事故中后期(即320 s至事故撤离),流量的变化呈现较为小的起伏波动规律,这一时间段的变化较为平缓.
(3)事故前期即(0~320 s时间段),交通流流量的呈现出较大的流速,最高达2500 pcu/h;事故中后期(即320 s至事故撤离),交通流流量呈现出较小的流速,整体的流速较为均衡.
1.3 事故1与事故2发生事故所占车道不同对该横断面实际通行能力影响的差异分析
采用控制变量法,使自变量尽量相同,因此在数据统计方面,有效数据统计的时间为事故发生一段时间之后,即从事故占用车道由1.5个车道变为2个车道时开始,到事故撤离时结束.
事故1中事故发生阻碍了第2、3车道的车辆通行,如图3所示.
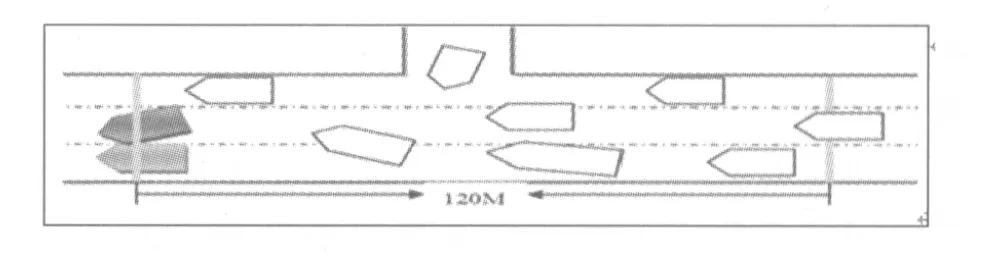
图3 事故1中事故发生时某一时刻简化图
事故2中事故发生占用了第1、2车道的车辆通行,如图4所示.
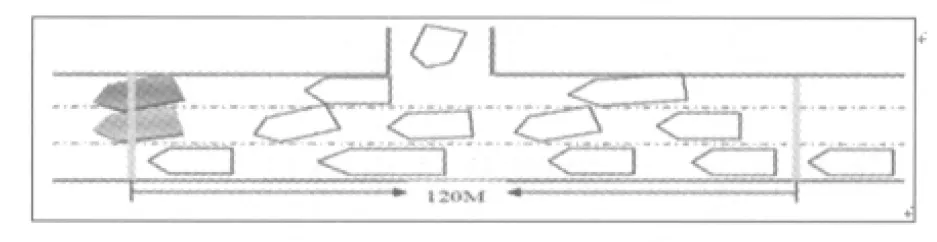
图4 事故2中事故发生时某一时刻简化图
1.3.1 车道交通流密度、速度及事故发生时间段引起的横断面实际通行能力的差异
根据事故1和事故2所统计出来的数据进行基本统计量的分析,分析结果如表1所示.

表1 基本统计量结果图
由表1分析可知,交通流密度、速度的不同也会造成横断面实际通行能力的差异,因此,车道交通流密度、速度引起事故1与事故2事故横断面实际通行能力的差异.
结合实际的分析,观测时间为17∶00-17∶40这一时间段的流量处于较小流量的平稳状态.
由生活经验得出:下班高峰期或人流拥挤时段,会引起事故1与事故2事故横断面实际通行能力的差异.
1.3.2 不同车道所占流量比例不同引起的横断面实际通行能力的差异
如图5所示,车道1、2、3对应右转、直行、左转流量比例分别为21%、44%、35% .

图5 附件3不同车道所占流量比例图
根据划分的不同事故时期,分别计算事故1和事故2中在不同事故时期内的平均密度与平均速度,进而计算出平均流量.数据统计如表2所示.
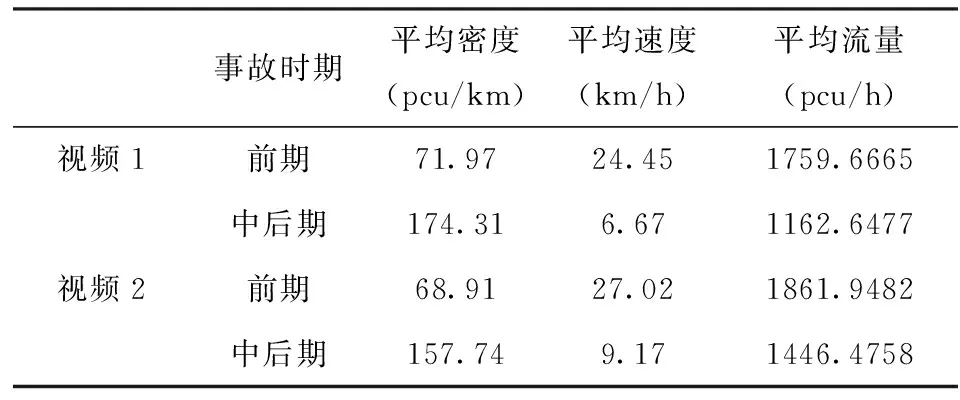
表2 事故1、2不同时期内的平均密度、速度、流量表
由上述分析得:占用第1、2车道比占用第2、3车道的交通流流量要大.因此分析得不同车道所占流量比例不同也会对横断面实际通行能力有影响.
1.3.3 造成事故1与事故2事故横断面实际通行能力差异的可能因素综述
造成事故1与事故2事故横断面实际通行能力差异的可能因素为:
(1) 不同车道交通流密度、速度存在差异;
(2) 事故发生所处时间段不同,事故2事故发生时段处于车流高峰期;
(3) 不同车道所占流量比例存在差异.
1.4 基于微分方程模型对事故路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间函数关系的求解
通过构建微分方程模型,分析事故1中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系.由1.1和1.2的分析可知实际通行能力与路段上游车流量都与时间有关,又因为排队长度和事故持续时间有关.因此对于此模型,首先采用微分方程对1.3的模型进行构建如下:
(7)
其中a,b为未知参数,L(t)为车辆排队长度,V(t)为实际通行能力,W(t)为路段上游车流量.其中,假设排队长度与实际通行能力成反比,排队长度与上游车流量成正比,而排队长度随时间的改变与实际通行能力倒数和上游车流量成正比.
其次采用多元线性回归模型对a,b进行求参.最后通过线性拟合模型,对L(t),V(t),W(t)进行拟合.即对假设的所有未知量求解,再通过积分的算法求出路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系.
利用SAS的多元回归分析对未知参数a、b进行求解,其结果如表3所示.
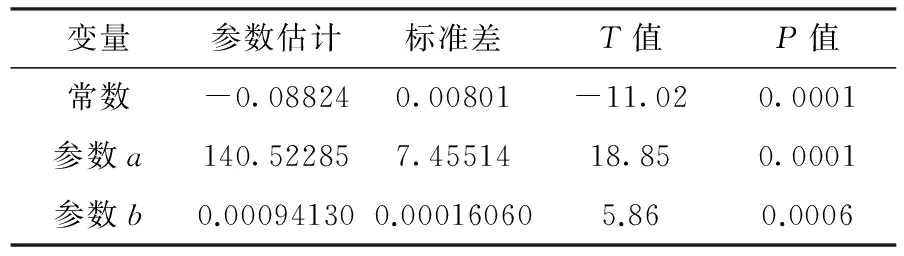
表3 参数估计和假设检验
(8)
得到函数
V(t)=0.13t3-4.85t2+45.72t+959.25
(9)
W(t)=-0.03t3+0.39t2-152.9t+1510.78
(10)
将得到的参数a、b以及函数v(t)w(t)代入原参数方程(8),得到参数方程为:
(11)
L(t)=4.57t4-127.43t3+642.23t2+
2014.13t-5.125
(12)
综上所述,得到结论:路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系为:
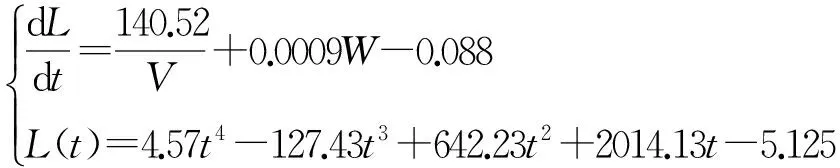
(14)
1.5 运用微分方程模型,对事故发生车辆排队长度将到达上游路口所需时间进行预测
通过1.3的求解,针对1.4已有的条件:横断面距离上游路口变为140 m,路段下游方向需求不变,路段上游车流量为1500 pcu/h,事故发生时车辆初始排队长度为零,代入1.4求出的微分方程(13),求出从事故发生开始,车辆排队长度将到达上游路口,所经过的时间.依题意,已知车辆排队长度L=140 m,路段上游车流量w=1500 pcu/h,代入模型:
L(t)=4.57t4-127.47t3+642.23t2+2014.13t-5.125
(15)
得到:当t=4.23 min时,车辆排队长度将到达上游路口.
2 模型的评价与推广
2.1 模型的评价
交通流-密-速模型,从物理的角度来看,可认为是宏观模型,对于宏观流体力学模型便于直观上把握交通流的整体特征,在简化的情况下容易得出解析解,给出交通流的基本行为;但是缺乏考虑各种真实交通条件的灵活性,不容易弄清楚产生交通流复杂行为的机制.
2.2 模型的推广
常微分方程推广模型,在经济学和管理科学中,我们常常研究有关经济变量的变化、增长、边际等问题.微分方程的理论足够完善的时候,利用它就可以精确地表示事物变化所遵循的基本规律.通常我们可以结合实际,从而建立微分方程模型.找出经济变量的变化规律并做出相应的决策和预测.常见的数学模型主要包括新产品推广模型、价格调整模型和人才分配模型.
参 考 文 献
[1] 邵敏华,孙立军.城市道路等效通行能力概念的提出及理论解释[J].同济大学学报(自然学科版),2008,36(3):310-314.
[2] 蒋启源,谢金星,叶 俊.数学模型(第四版)[M].高等教育出版社,2011.
[3] 李冬梅.道路通行能力的计算方法[J].河南大学学报(自然学科版),2002,32(2):24-27.
The Effect on Current Capacity of Road When Vehicle Lane Are Occupied
QIU Jia-li,ZHOU Xue-gang,ZHU Jia-peng,YE Yun
(Department of Applied Mathematics, Guandong University of Finance, Guangzhou 510521, China)
By making analysis on the data statistics of traffic flow when different lanes are occupied, this paper explores the changing process of the actual capacity of different lanes, and establish the traffic flow-dense-speed model. The functions of road vehicle queue length influenced by the traffic accidents actual current capacity of the accident section, accident duration, and section upstream traffic flow are obtained by establishing the differential equation models.
road current capacity;traffic-dense-speed model;multiple linear regression model;data fitting
2015-03-19
邱家理(1993-),男,本科,研究方向:信息与计算科学.
N34
A
1671-119X(2015)03-0051-04

