顾及系统误差的三维激光扫描坐标转换

贾象阳，姚吉利，马 宁，徐广鹏

顾及系统误差的三维激光扫描坐标转换

贾象阳，姚吉利，马 宁，徐广鹏

(山东理工大学，山东淄博255049)

一、引言

15年前，从世界上第一台地面扫描仪( terrestrial laser scanning，TLS)问世至今，扫描仪硬件性能已得到了很大提高，扫描技术由研究阶段发展成为顶级的商业化地理数据技术，三维激光使得三维扫描技术日趋成熟［1-3］，主要通过快速、准确地获取三维点云数据，进行地形测量和工业部件测量［2］，其在矿山测量、三维城市建模、变形观测、单个目标的实际三维成像、逆向工程等多个领域也有广泛应用［4-9］。由于地面扫描范围有限，只能用于工程测量。考虑到二维平面显示的实用性，三维坐标系统采用的形式除了( X、Y、Z)，还应有经纬度与高程( L、B、H)等多种形式［10］。工程测量中坐标系统( engineering surveying system，ESS)包括高斯平面坐标系统和高程系统。地面激光扫描仪坐标系统是三维直角正交坐标系，在工程测量中需将扫描点云坐标转换到工程测量坐标系中去，但是工程测量坐标系中通常选用高斯投影东坐标为X坐标、北坐标为Y坐标、正常高为Z坐标，组成三维右手直角坐标系，并不是严格的正交直角坐标系。扫描点之间的长度是地面上长度，工程测量坐标系点之间的长度是由X、Y反算的，两个坐标系的同名点长度不相等，其差值就是长度综合变形。

本文研究在尽量减小长度综合变形、大气折光和地球曲率系统误差的前提下，如何进行点云定向参数的高精度求解，找出系统误差对点云定向精度的影响规律，使扫描技术不但在平坦地区近距离进行扫描测量，还能在起伏大的山区进行远距离扫描测量。本文通过对工程测量坐标系中综合变形的产生进行分析，对三维扫描坐标转换模型进行改进，建立三维激光扫描坐标系与工程测量坐标系之间的转换模型，探求三维激光扫描坐标系与工程测量坐标系的转换方法，用于这两个坐标系之间的坐标转换，为地面扫描应用于精密工程测量寻求理论支持。

二、顾及系统误差的点云定向模型

三维正交坐标系之间的转换有相似变换［11-12］和综合变换［13］可以利用。扫描点云坐标属于三维正交坐标系坐标，因此只要把工程测量中非严格正交的三维点云控制点坐标转换成三维正交坐标系坐标，就能进行坐标转换。其坐标改正刚性改化公式为

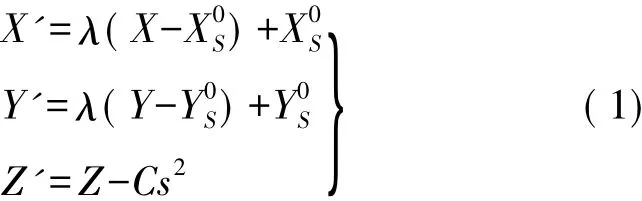
式中，( X0S，Y0S)为扫描站概略坐标; X、Y分别为标靶处的高斯东坐标和北坐标; ( X'，Y'，Z')为考虑综合变形的标靶坐标; Z为正常高;λ为扫描站处的边长投影变形和归算变形的系数; Hm为控制标靶的平均大地高，如果没有高程异常，平均大地高可用正常高代替; ym为标靶到中央子午线的平均值距离; Rm为扫描站处平均曲率半径;Δy是标靶到扫描站的横坐标之差;高斯平面C为大气折光误差和似大地水准面弯曲误差(类似于地球曲率引起的高程误差)的球气差系数; s为定向标靶到扫描站的水平距离。大气垂直折光系数K值一般在0．08～0．14之间，视工程精度要求确定C值是否需要测定，一般取K = 0．1。坐标刚性化定向参数解算的刚性化数学模型为

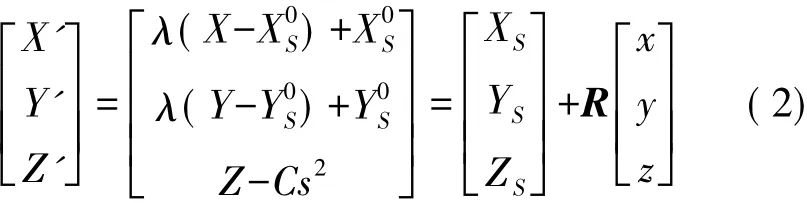
解算出刚性化点云定向参数后，将点云坐标先转换成刚性化坐标，然后按式( 3)

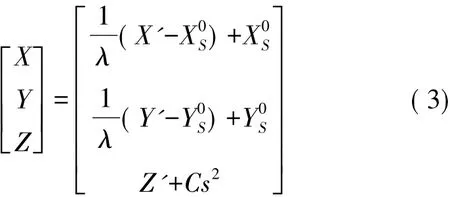
对刚性化坐标进行改正，得到点云的工程测量坐标系坐标。

三、试验分析

1．数据介绍

试验所用扫描仪器为Riegl VZ-1000，标靶使用自制球形标靶，共扫描5站，每站设4～5个球形标靶，其中相邻扫描站最少2个重合球形标靶，每站约4000万个扫描点。工程测量坐标系为1980西安坐标系，高斯投影的中央子午线为117°，扫描区所在经度为117°59'，高程系统选用1985高程基准。

2．试验方案

选工程测量坐标为观测值，扫描点云坐标认为是没有误差的常量。选用不同中央子午线的高斯坐标进行两种方案的点云定向:一是用未经刚性化的模型进行点云定向;二是采用式( 2)的刚性化模型。同一测区在中央子午线分别为116°、116°30'、117°、117°30'、118°时进行平差解算6个坐标转换参数，即未知参数为3个平移参数和3个旋转角，然后进行三维激光扫描坐标转换，并对这两个模型的坐标残差进行统计和比较分析，从中得到期望的结论。

3．试验数据分析

影响扫描坐标转换精度的因素是扫描点的扫描误差和定向参数求解误差。转换后扫描点位置误差很难用误差传播律计算得到，只能通过标准控制点的转换坐标与工程测量坐标系测量坐标( GNSS、全站仪测定)之差或坐标残差进行统计分析得到。扫描点位置误差包括X方向误差、Y方向误差、Z方向误差或高程误差、平面位置误差。按两个方案解算出不同中央子午线情况下的定向参数后，对定向标靶的坐标残差进行统计，结果如图1—图5所示。

图1 L0=116°的σX、σY、σZ比较

1)由图2—图4可以看出，随着扫描区距离中央子午线越远，刚性模型的坐标轴方向上的坐标残差离散度越大，误差曲线起伏较大，最大误差达到8 cm;本文的刚性化模型的误差曲线比较平缓，误差最大只有2．0 cm。

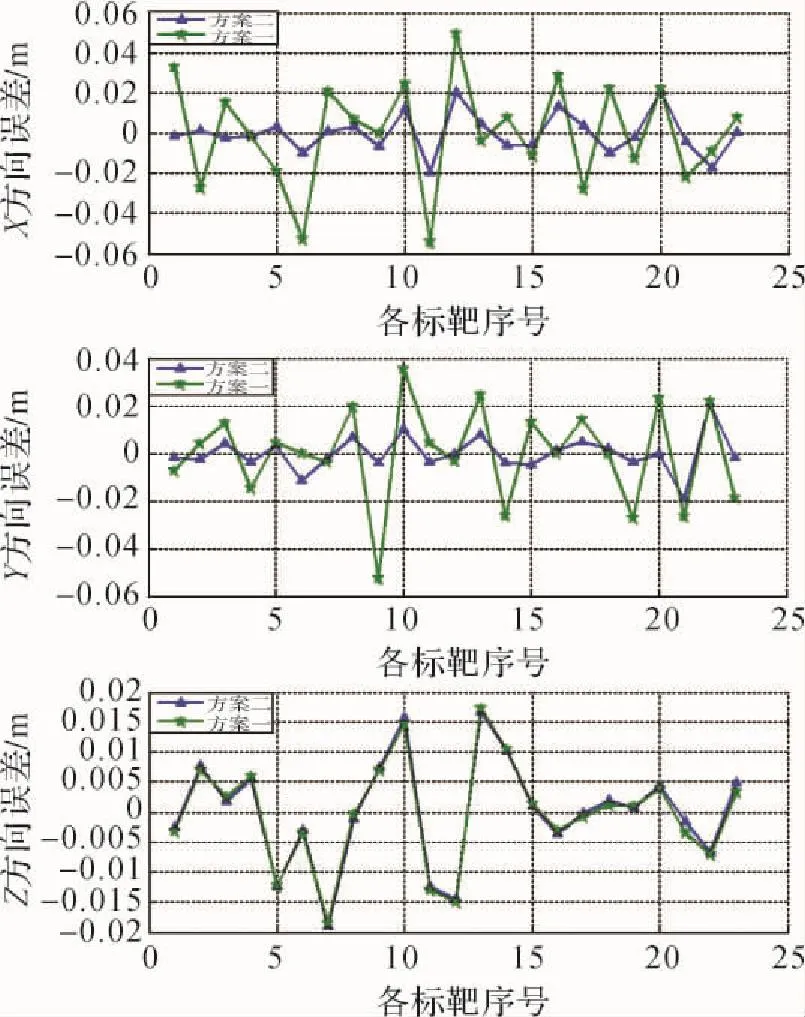
图2 L0=116°30'的σX、σY、σZ比较

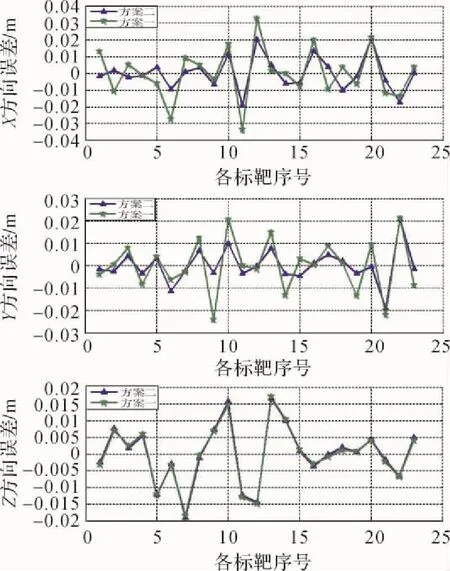
图3 L0=117°的σX、σY、σZ比较

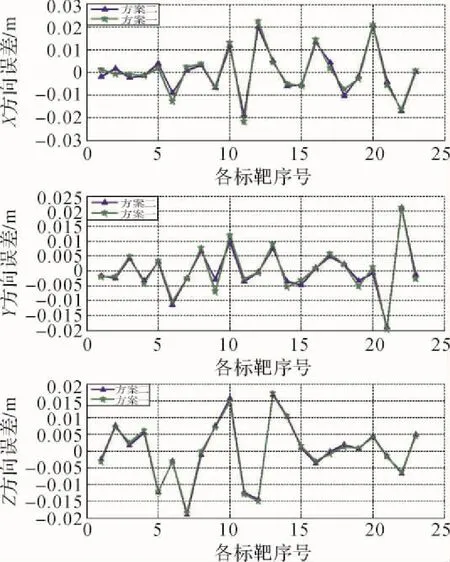
图4 L0=117°30'的σX、σY、σZ比较

2)由图5、图6可以看出，在离中央子午线0．5°范围内，两个方案坐标轴上误差在2．0 cm内，两条误差曲线基本一致，坐标误差相差不大。

3)由图2—图6得知，这两个方案的高程误差差变化不大，原因是扫描站离标靶的距离最大为273 m，这时的球气差影响相对于系统误差的影响可以忽略不计，因此对坐标转换的精度提高不明显。

4)用本文刚性化模型计算的5个扫描站的23个标靶转换后的平面位置中误差为12．4 mm，高程中误差为11．2 mm。对标靶中心工程测量中误差经过多次试验测定，标靶下方地面控制点用GNSS RTK观测2 min，平面点位误差为11．4 mm，高程误差为11．0 mm。其他如扫描误差、球心扫描坐标计算误差、标靶高度量取误差、刚性化模型误差等引起的综合平面误差为4．9 mm，引起的高程中误差为2．2 mm。

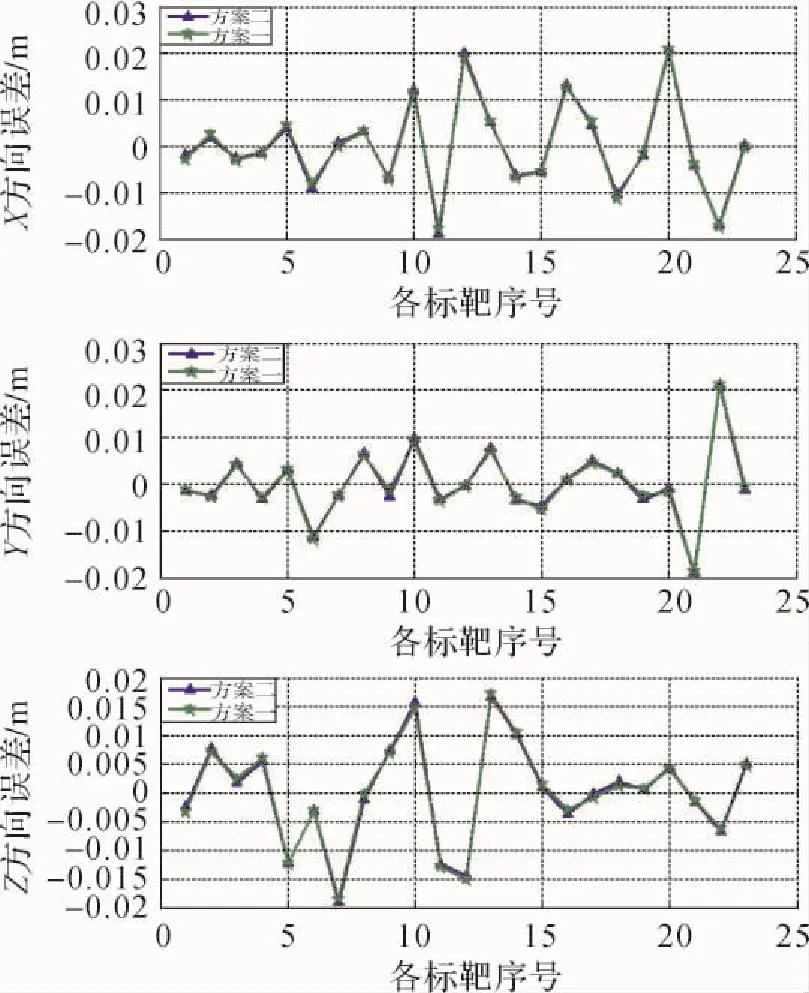
图5 L0=118°的σX、σY、σZ比较

四、结束语

本文提出的刚性化方法改进了现有的七参数坐标转换模型，减小了坐标转换参数解算的模型误差影响，如归算变形、投影变形和球气差对参数的影响，保证了坐标转换的精度。本方模型的转换后扫描点平面位置中误差变化不大，即扫描点平面位置中误差与扫描站到中央子午线的距离没有关系。而用传统刚性坐标转换模型解算的坐标转换参数含有长度综合变形综合影响，致使转换后扫描点平面位置误差急速非线性增大。因此，三维激光扫描技术用于工程测量时，根据工程的精度要求，测区距离中央子午线距离超过60 km时，应适当考虑点云定向模型误差的影响，选用合适的点云定向模型。

［1］ STAIGER R．Terrestrial Laser Scanning: Technology，Systems and Applications［C］∥2nd FIG Regional Conference．Marrakech:［s．n．］，2003．

［2］ LEMMENS M．Terrestrial Laser Scanning［M］∥Geo-information．Netherlands: Springer，2011: 101-121．

［3］ WANDA M，BERNER A，BOKELOH M，et al．Processing and Interactive Editing of Huge Point Clouds from 3D Scanners［J］．Computers＆Graphics，2008，32 ( 2) : 204-220．

［4］ BIOSCA J M，LERMA J L．Unsupervised Robust Planar Segmentation of Terrestrial Laser Scanner Point Clouds Based on Fuzzy Clustering Methods［J］．ISPRS Journal of Photogrammetry and Remote Sensing，2008，63( 1) : 84-98．

［5］ BARNEA S，FILIN S．Keypoint Based Autonomous Registration of Terrestrial Laser Point-clouds［J］．ISPRS Journal of Photogrammetry and Remote Sensing，2008，63( 1) : 19-35．

［6］ 姚吉利，刘科利，张磊．基于3D激光扫描的金属矿测量方法研究［J］．金属矿山，2011，40( 7) : 114-117．

［7］ FARDIN N，FENG Q，STEPHANSSON O．Application of a New in situ 3D Laser Scanner to Study the Scale Effect on the Rock Joint Surface Roughness［J］．International Journal of Rock Mechanics and Mining Sciences，2004，41( 2) : 329-335．

［8］ JOHN D L．Cavity Monitoring System and Stope Analysis ［C］∥Proceedings of Mass Min Chile 2004．Santiago: ［s．n．］，2004: 56-62．

［9］ MONSERRAT O，CROSETTO M．Deformation Measurement Using Terrestrial Laser Scanning Data and Least Squares 3D Surface Matching［J］．ISPRS Journal of Photogrammetry and Remote Sensing，2008，63( 1) : 142-154．

［10］陈俊勇．对我国建立现代大地坐标系统和高程系统的建议［J］．测绘通报，2002( 8) : 1-5．

［11］姚吉利，韩保民，杨元喜．罗德里格矩阵在三维坐标转换严密解算中的应用［J］．武汉大学学报:信息科学版，2006，31( 12) : 1094-1096．

［12］ 姚吉利．3维坐标转换参数直接计算的严密公式［J］．测绘通报，2006，( 5) : 7-10．

［13］杨元喜，徐天河．不同坐标系综合变换法［J］．武汉大学学报:信息科学版，2001，26( 6) : 509-513．

Three Dimensional Laser Scanning Coordinate Transformation with Taking Systematic Errors into Account

JIA Xiangyang，YAO Jili，MA Ning，XU Guangpeng

地面激光扫描仪设备坐标系是正交的三维直角坐标系，工程测量坐标系是用高斯平面坐标和高程来表达和研究三维实体的，不是严格正交的，用刚性三维坐标变换模型解算坐标转换参数，存在模型误差。因而本文提出了刚性化模型，顾及了归算和投影变形，以及大气折光和地球曲率等系统误差的综合影响，并在扫描区距离不同中央子午线的情况下，验证了刚性化模型可以有效消除系统误差的影响，从而保证了点云坐标转换后的精度及稳定性。

扫描坐标系;工程测量坐标系;刚性化模型;系统误差;平面点位中误差

贾象阳( 1989—)，男，硕士生，主要从事三维激光扫描点云定向及近景摄影测量研究。E-mail: ysy_941123@ sdut．edu．cn

P237

B

0494-0911( 2015) 11-0032-03

贾象阳，姚吉利，马宁，等．顾及系统误差的三维激光扫描坐标转换［J］．测绘通报，2015( 11) : 32-34．

10．13474/j．cnki．11-2246．2015．0340

2014-11-16

国家自然科学基金( 41074001)