考虑季度供电量二重性的最优GM（1，N）短期电量预测方法

冯天瑞，欧阳森，吴裕生，王克英

（华南理工大学 电力学院，广州 510640）

短期电量预测工作对电网的规划、安全经济运行和供电企业的营销工作具有重要的理论指导作用[1—3]。在短期电量预测中，月度电量序列和季度电量序列都具有周期波动性，但由于春节所在月份及全年最高电量出现月份的不固定，导致月度电量序列波动周期是不固定的，但春节必定在一季度，全年最高电量绝大多数情况出现在三季度，故季度电量序列的波动周期是基本固定的。因此可以认为，季度电量变化规律较月度电量更具周期性，预测结果也更为准确，可作为短期电量预测的基础数据[4]，并作为月度电量预测结果及年度电量预测结果准确性的判断标准。尤其是在历史数据较少的情况下，季度电量的参考价值更大。

但季度电量序列具有增长性和周期波动性的二重趋势，其中增长性往往不是简单的线性增长，而且周期波动性也呈现为一种复杂的非线性函数特性[5]，因此季节型电力负荷预测是一个困难的负荷预测问题，许多常规预测算法对季度供电量预测并不适用。考虑到可用于预测的季度电量数据量相对较少，故灰色预测模型在季度电量预测中被广泛采用。文献[6]采用GM（1,1）模型与人工神经网络（ANN）的组合预测算法对季度电量进行预测，但ANN算法较为复杂，不便于操作，同时2种算法的组合权重难以确定。文献[6]—文献[8]均使用基于灰色预测模型的算法，但均未考虑相关因素对电量的影响。文献[9]、文献[10]采用GM（1，N）模型对季度电量进行预测，引入外部影响因素对电量的影响，使对电量的预测更为客观。但以上文献均未计及供电量自身组分的信息，忽略了供电量自身重要组分的变化趋势对总供电量的影响。

此外，一个地区的总供电量由多个部分组成，这些部分即为总供电量的组分，可视为供电量变化的内因。这些组分保留并体现了区域用电量各部分最细致、最原始的特征，因此，需要对各组分进行分析，以更好地对区域总供电量进行预测。由于各组分用电量大小差别明显且趋势各异，故需要对各组分的重要程度进行分类，重点研究重要组分，忽略次要组分的影响，这样可在不影响预测精度的情况下，大大减少工作量，使预测工作更为简便。此外，随着城市的建设和经济的发展，供电量与经济指标间的关联度愈发紧密，经济指标亦可视为供电量变化的外因。因此，需要引入经济指标作为供电量的外部影响因素，通过分析经济指标的走势，预测供电量的发展变化趋势[11]。内因与外因的共同作用，导致季度电量序列出现了增长性与周期波动性的二重趋势，需要综合分析供电量变化的内因及外因，通过关联度计算得到各组分及外部影响因素的关联度并进行排序。按照关联度由大到小的顺序，依次增加一个影响因素与供电量历史值建立GM（1，N）模型，并根据预测效果选择影响因素个数N构建最优模型。该电量预测模型可同时计及内因、外因各自对电量序列的影响，即考虑季度电量序列的二重趋势。

本文综合考虑供电量自身组分以及外部重要影响因素对供电量发展变化趋势的影响，设计了考虑季度供电量二重性的最优GM（1，N）电量预测方法，用于供电量季度预测工作中。应用该模型对某供电局的电量数据进行预测分析，以验证该模型可以提高预测结果的准确性。

1 自身组分及外部影响因素分析

如上文所述，地区供电量由其自身各组分构成，又受到外部因素影响，故上述几部分的关系可用图1表示。

图1 季度供电量与自身各组分以及外部影响因素的关系

图1中，虚线箭头所指部分均不参与后续建模计算。总供电量由自身组分组成，受外部影响因素影响。

1.1 供电量自身组分分析

对供电量自身组分的划分，即为对不同类型、不同行业电力用户的划分。不同用户用电变化趋势对总供电量的影响不同，甚至某些类型用户的用电趋势可以主导总供电量的变化趋势。因此，有必要对供电量的重要组分进行分析，并分析各行业用电对总供电量的影响。

目前，我国根据电价和负荷特性将用户分为工业用户、非工业用户、居民用户、商业及其它用户等5种类型。该5种类型即为自身组分中的1级组分。可根据实际情况，将上述5种1级组分划分为1级重要组分和1级次要组分，其中1级次要组分不参与后续建模计算。之后对1级重要组分进行划分，分为2级重要组分和2级次要组分。其中，2级重要组分参与最优GM（1，N）建模，2级次要组分不参与最优GM（1，N）建模。

1.2 外部影响因素分析

影响供电企业供电量的外部影响因素众多，按其重要程度可分为外部重要影响因素与外部次要影响因素。其中，外部重要影响因素等级与2级重要组分相同，参与最优GM（1，N）建模。外部次要影响因素不参与最优GM（1，N）建模。

若计及各级次要组分和外部次要影响因素，本文所提出的方法依然适用，但建模及计算的工作量将大大增加，故本文不讨论计及各级次要组分和外部次要影响因素的情况。

为便于叙述，下文将“供电量自身组分”与“外部影响因素”统称为“影响因素”。

2 算法设计

2.1 算法步骤及其流程

本文所设计的考虑季度供电量二重性的最优GM（1，N）电量预测方法的流程如图2所示。

（1）数据输入。需要输入的数据包括2级重要组分历史数据以及外部重要影响因素数据。

（2）最优GM（1，N）建模。利用（1）中输入的参数进行最优GM（1，N）建模，得到最优GM（1，N）模型。最优GM（1，N）建模方法将在2.2节中详细介绍。

（3）影响因素预测。使用常用预测算法对所有影响因素进行预测，为使用最优GM（1，N）模型进行预测计算准备数据。

（4）预测计算。利用（2）中得到的最优GM（1，N）模型及（3）中得到的影响因素的预测值进行预测计算。

（5）预测结果输出。

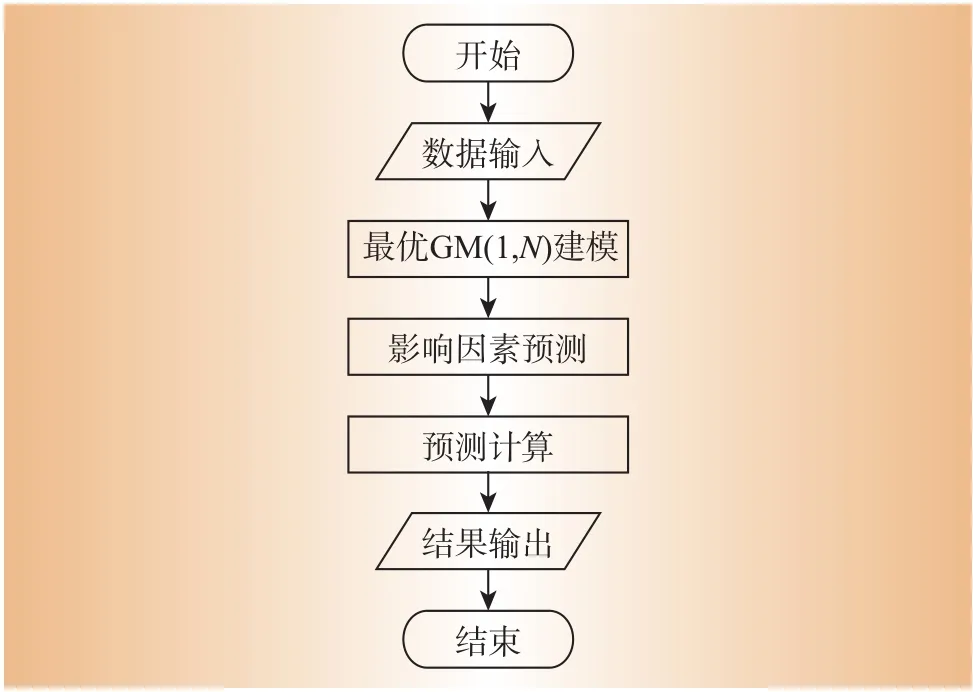
图2 算法流程图

2.2 最优GM（1，N）建模

最优GM（1，N）建模涉及各影响因素与供电量之间关联度的计算以及利用关联度进行最优GM（1，N）建模的方法。下文将从这2方面分别进行介绍。

2.2.1 关联度计算方法

关联度就是表征事物之间关联程度的量度，实际即为曲线几何形状之间的比较，即几何形状越接近，发展变化趋势和规律就越相似，关联度就越大。供电量的关联度分析就是分析影响因素与供电量之间的关联关系。常用的关联度分析方法有：邓氏关联度、绝对关联度、斜率关联度等分析法。本文采用斜率关联度，其步骤如下。

·计算斜率·计算关联系数

·计算关联度

式中：i=1,…,n；t=1,…,（m－1）；m为样本容量；n为影响因素个数；σi为影响因素Xi的标准偏差；-Xi为影响因素Xi的平均值；X为供电量参考序列。

由以上3式即可算出各影响因素与供电量之间的关联度。

2.2.2 最优GM（1，N）建模方法

GM（1，N）模型对N-1个影响因素用一阶微分方程建立灰色模型，可以用来建立供电量与N-1个影响因素之间关系的预测模型，适用于对多影响因素系统作分析及预测[12]。

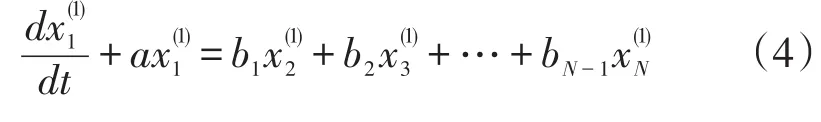
利用新生成的数据序列进行累加生成，得到生成序列后建立一阶微分方程再利用最小二乘法解得参数（a,b1,b2,…,bN－1），从而得到系统的状态方程

式中：k=1,…,m。式（5）再累减还原，即可得到预测公式

GM（1，N）预测模型不苛求影响因素的完备性，但重视影响因子的关联质量[13]，且对N有最优条件。用该模型预测供电量，应根据对各影响因素的关联度排序，选择最优参数N来构造GM（1，N）模型。本文的参数N的选择方法流程如图3所示。

图3 建立最优GM（1，N）模型的流程图

（1）输入数据。需要输入的数据即为图2流程图中的数据，包括2级重要组分历史数据以及外部重要影响因素数据。

（2）计算电量与各影响因素的关联度。

（3）对上一步计算出来的关联度按照由大到小的顺序进行排序（n为影响因素个数）。

（4）根据关联度的大小，依次增加一个影响因素建立GM（1，N）模型，并计算该GM（1，N）模型对历史数据的拟合值，进而计算其拟合均方误差。

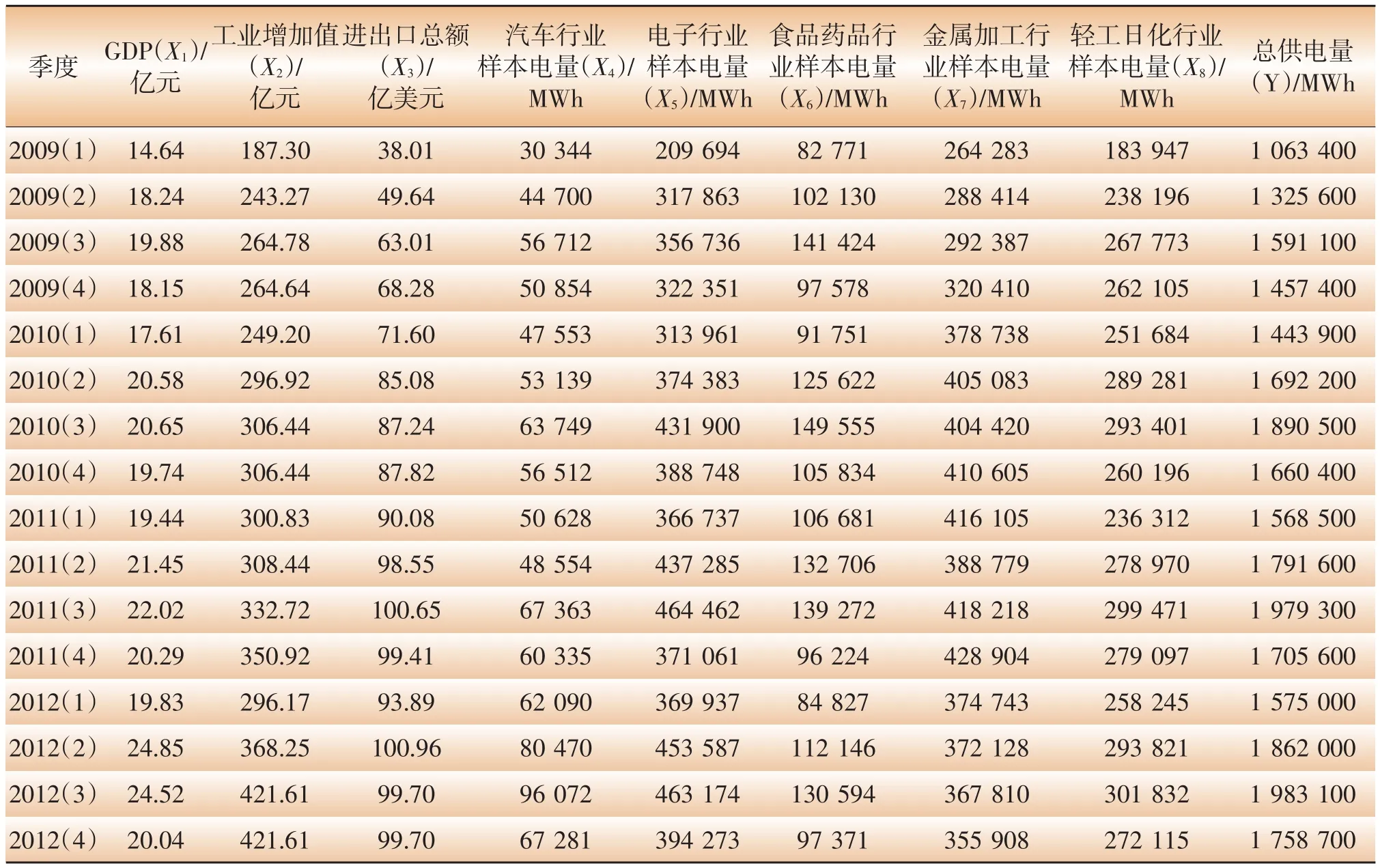
表1 某供电局供电量、影响因素季度统计数据

（5）选取均方误差最小时的参数N，该参数N所对应的GM（1，N）模型即为最优GM（1，N）模型。

最优GM（1，N）模型不仅引入了影响因素建立预测模型，同时利用关联度对影响因素进行排序，再根据关联度的大小，依次增加一个影响因素来建立GM（1，N）模型，从而不仅保证了对影响因素的筛选，还通过寻优的方法确定N值，从而减少建模时的主观性和随意性，提高了模型预测结果的准确性和可靠性。

3 应用实例

本文采用某供电局的实际供电量数据对本预测方法进行检验，与采用普通GM（1,1）模型的预测结果进行比对。

3.1 实例数据

表1为某供电局2009—2012年的供电量、影响因素季度统计数据。

某供电局供电量数据具有以下特点：①只有2009—2012年的供电量历史数据，数据量相对较少；②该供电局所供电地区大宗工业用电占比达90%左右，农业、商业、居民等用电量占比小，因此，本文仅将大宗工业用户视为1级重要组分。结合该供电局所供电地区的实际情况，本文将大宗工业用户分为汽车、电子、食品药品、金属加工、轻工日化共5个行业（即5个2级重要组分）。考虑该地区经济发展实际情况，本文选取GDP、工业增加值、进出口总额3项经济指标作为外部重要影响因素[14]。

实际应用中，2级组分的划分不局限于大宗工业，可根据实际情况调整行业分类，以更好对用电量进行准确预测。

3.2 建立最优GM（1，N）模型

表2为利用关联度计算求出8个影响因素与总供电量的关联度。

表2 各影响因素与供电量季度数据的关联度

由表2可得各影响因素与供电量之间的关联度大小顺序。

利用图2的流程图和表1中的数据选择最优参数N建立最优模型。其中，不同影响因素个数的GM（1，N）模型的相对误差平均绝对值见表3。

表3 不同N时GM（1，N）模型的误差

由表3可知，当N为9时，模型最优，预测结果的相对误差平均绝对值最小，为0.45%，预测精度高，因此本文采用了N=9建立最优GM（1，9）预测模型。虽然本文选择N为9建立预测模型，但是从表3中可以看出，并不是N越大拟合效果越好，如表3中N为5的拟合效果比N为6的拟合效果好。

3.3 基于最优GM（1，N）模型的预测分析

在应用预测模型GM（1，9）对2013年的季度供电量进行预测时，必须知道8个影响因素在预测期内的数值。因此，还需对电子行业、轻工日化行业样本、GDP、汽车行业、工业增加值、进出口总额数据、金属加工行业、食品药品行业等8个影响因素进行预测。对8个影响因素的预测采用优选组合预测算法，涵盖了目前较为成熟的单一预测算法[15]。所采用的单一预测算法均可综合考虑季度电量数据存在的增长性及季节波动性特征。8个因素的预测结果见表4。

将以上数据代入GM（1，9）模型，得到2013年季度电量预测值。同时，使用不考虑自身组分及外部影响因素的GM（1，1）模型计算进行对比。GM（1，9）模型的预测结果以及2种模型的相对误差对比如表5所示。

由表5可以看出，2013年的第1、3季度的预测相对误差为0.41%、-0.43%，精度较高；第2、4季度的预测相对误差为-2.19%、1.32%，预测精度虽低于对1、3季度的预测，但均远高于GM（1，1）的预测精度，故可证明本文建立的GM（1，9）预测模型精度良好，预测结果准确度较高。

通过对年度供电量总和的比较可以看出，将本方法所得4个季度的供电量加和得到年度电量预测值，该预测值与实际值的相对误差仅为-0.27%，具有较高的精度。故本方法也可推广至年度供电量的预测工作中。

4 结论

（1）季度供电量受众多因素影响，其二重趋势由内因、外因共同造成。故对其预测需要综合考虑内因及外因共同对其发展变化所造成的影响。

（2）对供电量自身组分进行分层级的重要性划分，忽略次要组分，重点研究重要组分，可在不影响精度的情况下，减少工作量。这在实际应用中也得到了验证。

（3）利用关联度计算求影响因素的关联度，并进行排序，从而明确各影响因素的重要性。

（4）从关联度由大到小逐一增加影响因素个数，通过寻优方法建立一个参数最优的GM（1，N）模型，该模型实现了对影响因素的择优选择，从而具有一定的可靠性。

（5）实例分析表明，本文算法具有较好的精度，预测结果可信度也较高。

本文综合考虑了季度电量存在的增长性及季节波动性的复杂二重趋势，提出了以最优GM（1，N）模型为核心的电量预测方法。该方法以保留了电量发展最原始、最细致规律信息的2级重要组分以及能反映外部因素对电量发展影响的外部重要影响因素为输入，对季度供电量进行预测。本方法输入数据较为简单，预测精度较高，适合在电量预测工作中推广应用。

表4 8个影响因素的2013年预测值

表5 2013年4个季度的供电量预测结果

[1]Pessanha J F M,Leon N.Long-term forecasting of household and residential electric customers in Brazil[J].IEEE(Revista IEEE America Latina)Latin America Transactions,2012,10(2)：1 537-1 543.

[2]毛李帆，江岳春，龙瑞华，等.基于偏最小二乘回归分析的中长期电力负荷预测[J].电网技术，2008，32（19）：71-77.

[3]Kandil M S,El-Debeiky S M,Hasanien N E.Long-term load forecasting for fast developing utility using a knowledge-based expert system[J].IEEE Trans onPower Systems,2002,17(2)：491-496.

[4]潘小辉，刘丽萍，李扬.提高月度售电量预测精度的一种新方法[J].电力需求侧管理，2013（3）：11-15.

[5]牛东晓，陈志业，邢棉，等.具有二重趋势性的季节型电力负荷预测组合优化灰色神经网络模型[J].中国电机工程学报，2002，22（1）：29-32.

[6]牛东晓，陈志业，谢宏.组合灰色神经网络模型及其季节性负荷预测[J].华北电力大学学报：自然科学版，2000，27（4）：1-6.

[7]李金颖，牛东晓.非线性季节型电力负荷灰色组合预测研究[J].电网技术，2003，27（5）：26-28.

[8]刘秋华.基于季节指数和灰色预测的月电量预测模型[J].南京工程学院学报：自然科学版，2006，4（1）：1-6.

[9]樊爱宛，潘中强，王巍.灰色GM（1，N）模型在河南省煤炭需求预测中的应用[J].煤炭技术，2011，30（10）：7-9.

[10]白福臣.灰色GM(1，N)模型在广东海洋经济预测中的应用[J].技术经济与管理研究，2009（2）：9-11.

[11]韩丹，张宏波，贾勇.经济因素对电量的影响分析与预测[J].吉林电力，2009，37（3）：16-19+27.

[12]刘思峰，党耀国.灰色系统理论及其应用[M].北京:科学出版社，2004.

[13]张勇军，石辉，翟伟芳，等.基于层次分析法—灰色综合关联及多灰色模型组合建模的线损率预测[J].电网技术，2011，35（6）：71-76.

[14]朱继萍，戴君.中长期电力负荷预测相关影响因素优化选择[J].计算机仿真，2008，25（5）：226-229.

[15]康重庆，夏清，沈瑜，等.电力系统负荷预测的综合模型[J].清华大学学报：自然科学版，1999，39（1）：8-11.