基于解析时间波场外推与波场分解的逆时偏移方法研究
胡江涛, 王华忠
同济大学海洋与地球科学学院波现象与反演成像研究组, 上海 200092
基于解析时间波场外推与波场分解的逆时偏移方法研究
胡江涛, 王华忠
同济大学海洋与地球科学学院波现象与反演成像研究组, 上海 200092
双程波方程逆时深度偏移是复杂介质高精度成像的有效技术,但其结果中通常包含成像方法引起的噪音和假象,一般的滤波方法会破坏成像剖面上的振幅,其中的假象也会给后续地质解释带来困扰.将波场进行方向分解然后实现入射波与反射波的相关成像能够有效地消除这类成像噪音,并提高逆时偏移成像质量.波传播方向的分解通常在频率波数域实现,它会占用大量的存储和计算资源,不便于在沿时间外推的逆时深度偏移中应用.本文提出解析时间波场外推方法,可以在时间外推的每个时间片上实现波传播方向的显式分解,逆时深度偏移中利用分解后的炮检波场进行对应的相关运算,实现成像噪音和成像信号的分离.在模型和实际数据上的测试表明,相比于常规互相关逆时偏移成像结果,本文方法能够有效地消除低频成像噪音和特殊地质构造导致的成像假象.
解析时间波场外推; 波场分解; 噪音消除; 逆时深度偏移
1 引言
基于双向波波动方程的逆时偏移方法(Baysal et al.,1983; McMechan, 1983; Whitmore, 1983)克服了Kirchhoff偏移的焦散和单走时问题,单向波波动方程的陡倾角成像限制问题,成为复杂介质高精度成像的有力工具.借助GPU和多核CPU等高性能计算设备的发展(刘红伟等,2010; 李博等, 2010; 刘守伟等, 2013),逆时偏移方法已经被广泛应用于工业生产中.但其成像结果通常存在一定的、由成像方法引起的成像噪音和假象,这是由于不对应的波场进行相关成像而引起的.
低频成像噪音是逆时偏移成像中最常见的问题.在速度模型中存在高波数的速度扰动或反射界面时,正、反传波场中存在较强的背向散射(或反射),低频成像噪音非常严重.Loewenthal 等(1987)采用平滑速度场的方式来消除背向散射波场进而消除低频噪音.Fletcher 等(2006)采用压制反射界面背向散射的方式来消除低频噪音.Yoon et和Marfurt (2006)、康玮和程玖兵(2012)采用波印廷矢量方法进行波场传播方向预测,实现成像结果的角度切除,进而消除低频噪音.Guitton 等(2007)采用最小平方滤波的方式实现低频噪音消除.Zhang和Sun(2009)采用Laplace滤波方法来进行低频噪音消除,并通过频率波数域关系实现了Laplace滤波的振幅校正.Liu 等 (2007, 2011)提出采用波场分解方式来构造逆时偏移成像条件,实现入射波和反射波的相关成像,进而达到消除低频噪音的目的.杜启振等(2013)对上述低频噪音压制方法做了详细分类并对比了各种方法的优缺点,指出基于波场分解的成像方式在复杂介质中能更好地消除低频噪音和实现振幅保真.
除了低频成像噪音,Fei 等(2010,2014)分析了逆时偏移对偏移速度的敏感性,并指出在速度模型精度较差时,当向斜构造存在强速度梯度时,逆时偏移会产生较强的假象.产生这类假象的构造通常会出现在岩丘边界,潜山顶面及火成岩与围岩的接触面等地方.他指出在这类构造区域,采用波场分解成像方式能够有效地消除成像假象.虽然波场分解成像能够有效地消除成像噪音,但它通常需要在频率波数域进行实现.在逆时深度偏移过程中,波场分解通常需要将炮点和检波点波场存盘并进行关于时间的傅里叶变换,而在沿时间的外推过程中,时间维处于数据的最慢维,因此一般的波场分离成像条件的I/O量和计算量非常大.
针对上述问题,本文提出了解析时间波场外推及波场分解方法.在逆时深度偏移过程中,仅利用外推过程中的、每个时间步的解析时间波场进行不同传播方向的波场的显式分离,避免了时间域向频率域转换的I/O量和计算量.方向分解后的波场进行对应的波场相关可以有效地压制成像噪音和假象.模型和实际数据的测试表明了所提出方法的有效性.
2 逆时深度偏移及波场分解成像条件

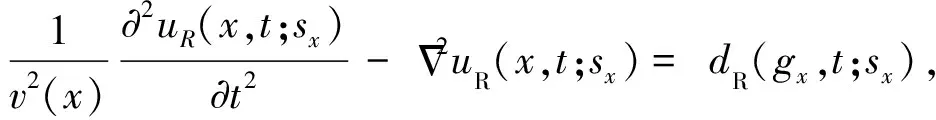
(2)其中,dR为检波点端接收的炮波场,gx=(gx,gy)为检波点空间位置,uR为延拓后的检波点波场.
双向波沿时间的正向和反向外推可以模拟声波方程(1)和(2)所能模拟的所有波现象,在偏移速度场比较精确的情况下,理论上可以对一次和多次散射(和反射)波进行偏移成像.这是逆时深度偏移成为复杂介质成像首选方法技术的原因.存在的问题是计算代价大和不对应的波场相关产生的噪音和假象.一般地,后者需要更改成像条件来解决.
本文采用有限差分方法求解公式(1)和公式(2)来实现波场的延拓.将延拓的波场应用如下的零延迟相关成像条件即可提取地下界面的成像结果,
(3)
其中,tmax为延拓的最大时间值.
在速度模型比较准时,炮点正向外推和检波点反向外推波场都会产生前向和背向散射(和反射),炮点和检波点波场中同方向传播的波场相关产生低频噪音,某些反方向传播的波场会形成成像假象(Liuetal. 2011;Feietal.,2010).因此可以利用波场的方向分解来实现相对应波场的相关,进而压制低频噪音和/或成像假象.
Liu等(2007)提出将炮点波场和检波点波场进行上下行波分解:
(4a)
(4b)
其中,上标up代表上行波,down代表下行波.需要说明的是,Liu等(2007)所指炮检端的上下行波是从炮点端来看的,其上下行波的定义与单向波方程的上下行波定义一致.
将公式(4)带入公式(3),可得出相关成像的结果为
=I1(x)+I2(x)+I3(x)+I4(x),
(5)
其中,I1(x)为炮点下行波场与检波点上行波场相关成像结果,I2(x)为炮点上行波场与检波点下行波场相关成像结果,I3(x)为炮点下行波场与检波点下行波场相关成像结果,I4(x)为炮点上行波场与检波点上行波场相关成像结果.在速度模型精度较高时,I1(x)和I2(x)分别是炮检波场中反向传播的波场的相关,对应为反射界面(或散射点)的像.Fei等(2014)指出在速度模型精度不是太高时,I2(x)在特殊地质构造区域可能导致成像假象.I3(x)和I4(x)分别是炮检波场中同向传播波场的相关,表现为低频噪音.由公式(5)也可看出,采用波场分解成像条件可以有效地实现逆时偏移成像噪音和成像信号的分离.
3 解析时间波场外推及波场分解
虽然波场分离成像条件能够有效地分离逆时偏移中的信号和噪音,但是波场分解方法是其实现的核心.下面以炮点波场为例来说明波场分解过程,检波点波场的方向分解与其类似,不再赘述.波场方向分解通常借助傅里叶变换来实现,波场的时间和空间傅里叶变换可以表示为
×e-i(ω t+xkx+yky+zkz)dtdxdydz.
(6a)
波场的上下行波的定义为
(7a)
(7b)
同理可以定义左右行波和前后行波.由公式(7)可以看出波场的方向由频率和波数的符号共同决定,也就是说常规波场分离需要在频率域进行实现.时间域逆时偏移实现常规波场分离,需要将地下波场存盘,并进行关于最慢维的时间傅里叶变换,所以其I/O量和计算量很大.但是时间域外推中比较便于在波场时间片上获取空间波数信息,所以为了提高计算效率,Liu等(2011)根据频率和波数的符号关系推导出
(8)
其中,
(9a)
(9b)
(9c)
(9d)

由公式(7)和公式(8)可以看出,波场的显式分离需要由频率和波数的符号共同决定,而为了实现的高效,需要尽量利用空间波数的符号来进行波场分离.那么如果能够获取一个时间波场,其频谱仅包含正或负频率,那么波场的方向分解就可以依靠空间波数的符号来实现.这样的时间信号在信号处理中广泛应用,这就是复信号,也即解析时间信号.解析时间信号的实部为信号本身,而虚部为信号的Hilbert变换.将解析时间信号概念扩展到波场上,我们将其称为解析时间波场.通过常规波场传播方程可以获得波场本身(即解析时间波场的实部),但是无法获得波场的Hilbert变换(即解析时间波场的虚部).可以对地下波场进行Hilbert变换来实现解析时间波场虚部的构造,但Hilbert变换为一个时间方向的卷积,这就需要将波场存盘并进行卷积运算,I/O量同样会增加.Hilbert变换为一个90°相移运算,在频率域是一个相位滤波器.而波场传播算子为线性算子,也即传播方程(1)和(2)的源项和波场成线性关系(Liuetal., 2006).那么参考波动方程相位编码的实现(Liuetal., 2006),可以对波动方程的源项进行Hilbert变换.由于波场传播算子的线性特征,波场也进行了90°相位移动,这样就获得了解析时间波场的虚部.炮点的解析时间波场外推可以表示为
(10)

(11)


(12a)


(12c)
(12d)其中,Re代表取实运算.同样,可以写出检波点的上下行波:
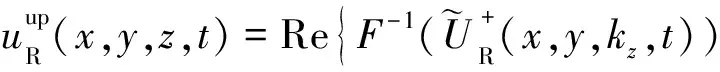
(13a)
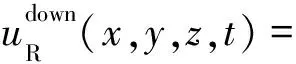
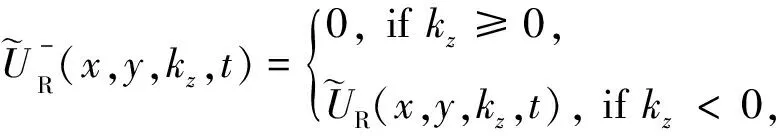
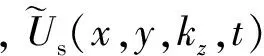
4 数值试验
为了测试方法的有效性,下面采用向斜模型进行测试,如图1所示.该模型第一层,第二层和第三层速度值分别为2000m·s-1, 2200m·s-1和4500m·s-1.第二层和第三层之间在实际情况可能为岩丘边界,火成岩边界及潜山顶面等地质构造.模拟数据一共100炮,炮间隔为50m,最大偏移距为4000m.采用常规相关逆时偏移成像方法得到的结果如图2所示,由图可以看出,成像结果受到严重的低频噪音影响.

图1 准确速度模型Fig.1 Exact velocity model

图2 传统逆时偏移成像结果Fig.2 Result of conventional RTM
下面利用例子来验证本文分解方法的有效性.图3为采用本文解析时间波场外推方法得到的CDP号为380位置处的解析VSP记录,其中炮点布设在CDP号为300位置处.采用常规波场外推方法仅能得到该解析VSP记录的实部.图4为常规实波场和解析波场在0.5s时间片上的垂直波数谱对比.由图3可以看出该记录在0.5s时间片上仅存在下行波记录.而常规实波场的波数谱并不能指示这一信息,所以常规波场分离方法通常在频率域实现.但在本文解析时间波场的波数谱上则可以清楚地识别该下行波记录.利用本文波场分解方法在每个时间片上进行上下行波分解可以得到分离的上下行波记录,如图5所示.
在成像空间应用上述波场分解方法将波场分解为各个方向矢量,然后进行成像,得到的炮点下行和检波点上行成像结果如图6a所示,炮点上行和检波
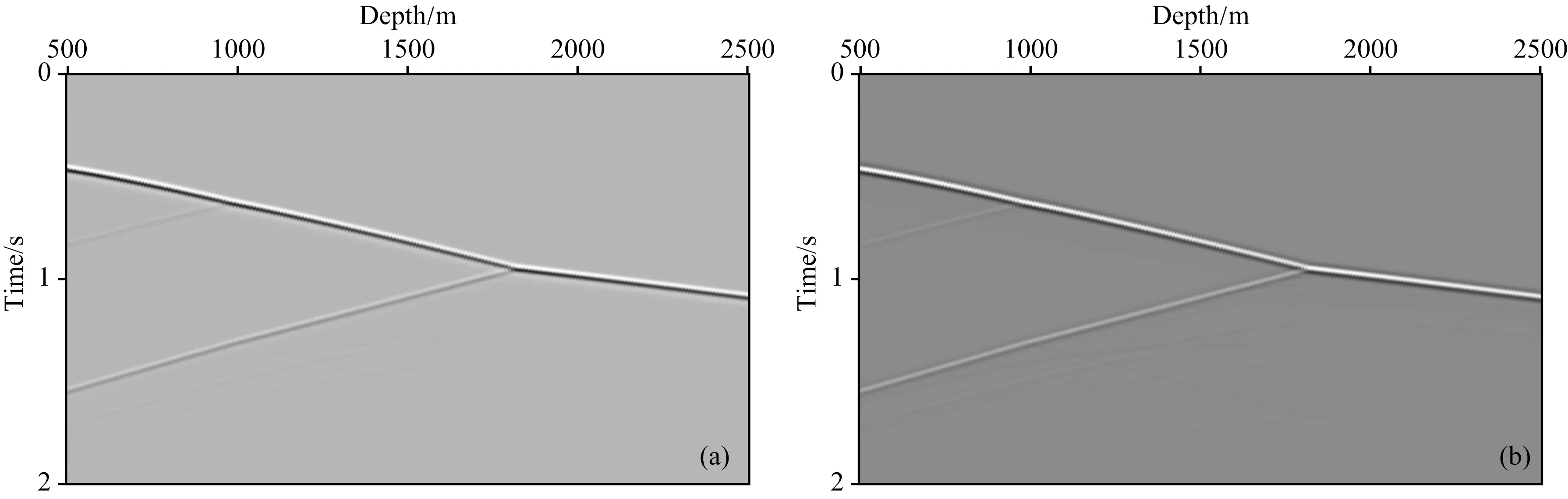
图3 解析VSP记录(a)解析VSP记录实部; (b)解析VSP记录虚部.Fig.3 Analytic VSP record(a) Real part of analytic VSP record; (b) Imaginary part of analytic VSP record.

图4 波数谱对比图(a)常规实波场波数谱;(b)解析波场波数谱.Fig.4 Comparison of wavenumber spectrums(a) Wavenumber spectrum of conventional real wavefield; (b) Wavenumber spectrum of analytic wavefield.
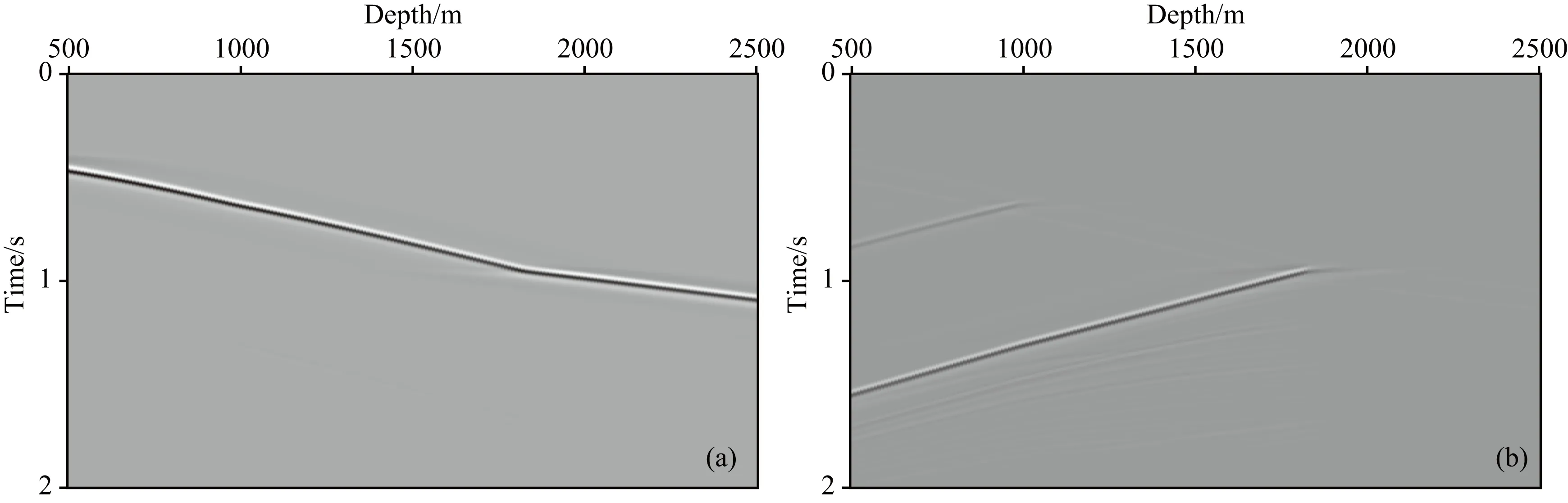
图5 分离的上下行波(a)下行波记录;(b)上行波记录.Fig.5 Separated up and down going wavefield(a) Down-going wavefield; (b) Up-going wavefield.

图6 波场分离成像结果(a)炮点下行与检波点上行成像结果;(b)炮点上行与检波点下行成像结果;(c)炮点下行与检波点下行成像结果;(d)炮点上行与检波点上行成像结果.Fig.6 Results of wavefield separation imaging(a) Result from down going source and up going receiver wavefield; (b) Result from up going source and down going receiver wavefield; (c) Result from down going source and down going receiver wavefield; (d) Result from up going source and up going receiverwavefield.
点下行成像结果如图6b所示,炮点下行和检波点下行成像结果如图6c所示,炮点上行和检波点上行成像结果如图6d所示.由图可以看出,图6a和图6b为有效信号,而图6c和图6d为低频噪音.由图也可以看出,本文方法可以实现各个成像分量的分离.在这种速度模型比较精确的情况,可以叠加图6a和图6b结果作为最终成像结果,也即等效波场分离成像公式结果.在这种情况下,等效波场分离成像条件的结果和本文方法结果等价.
在实际情况下,由于速度建模方法对速度结构的分辨能力限制,通常只能得到一个相对平滑的速度模型.将准确速度模型进行平滑来模拟实际情况,平滑速度模型如图7所示.采用常规相关逆时偏移成像,结果如图8a所示.由图可以看出,其结果存在一定的低频噪音,还存在一定的成像假象.采用本文方法提取炮点下行和检波点上行成像,炮点上行和检波点下行成像的叠加结果如图8b所示,该结果等价于等效波场分离成像公式得到的结果.由图8b可以看出,相比于图8a,成像假象明显减少,但是在向斜的中心存在一个较强的成像假象,且该假象呈现与向斜构造相似的形态.这个假象产生的主要原因为:由于第二层和第三层之间存在强速度分界面,因此平滑速度模型中存在强梯度速度过渡带,当炮点和检波点波场经过这一区域时,都会产生向上回传的波场,而由于向斜独特的地质形状,导致炮点上行波和检波点下行波场都汇聚到向斜中心,进而在应用成像条件时产生假象.由此,可以看出这类假象是由炮点上行和检波点下行波场进行相关所导致的.采用本文方法分别提取炮点下行和检波点上行成像如图8c所示,炮点上行和检波点下行成像结果如图8d所示.由图可以看出,图8c为有效信号,而图8d则是图8b所包含的假象.在实际情况下,这种假象可能导致岩丘边界、潜山面及火成岩边界的错误解释.由图8c和图8d也可以看出在这种情况下,本文方法相比于等效波场分离成像条件能够更好地分离各个成像分量,进而消除假象.

图7 平滑速度模型Fig.7 Smooth velocity model

图8 成像结果对比(a)传统成像结果;(b)等效波场分离成像结果;(c)炮点下行与检波点上行成像结果;(d)炮点上行与检波点下行成像结果.Fig.8 Imaging results comparison(a) Result of conventional RTM; (b) Result from equivalent wavefield imaging condition; (c) Result from down going source and up going receiver wavefield; (d) Result from up going source and down going receiver wavefield.

图9 不同偏移方法成像结果的对比(a)相关成像结果;(b)Laplacian滤波方法;(c)波场方向分解方法.Fig.9 Comparison of imaging results from different methods(a) Result of correlation imaging condition; (b) Result from Laplacian filter; (c) Result from wavefield separation method.
下面对比本文方法与常规滤波方法在噪音消除方面的表现.Laplacian滤波方法由于其高效性而被广泛应用于低频噪音消除中,因此,这里将本文方法与该方法进行对比.测试的模型为一个两层速度模型,速度分界面在1500m处,第一层速度为2000m·s-1,第二层速度为2500m·s-1.由该模型速度分界面的速度差异可以得出:在该模型上,低频成像噪音强度较弱,同时成像噪音仅分布在成像子波之上.这样,利用相关成像方法得到的成像子波就可近似地作为其他成像方法在成像振幅保真度方面的参考.图9展示了相关成像方法、Laplacian滤波方法以及本文波场分解方法的结果.由图可以看出,Laplacian滤波方法和本文波场分解方法都较好地对低频背景噪音进行了去除.但是对比二者能量关系可以发现,Laplacian滤波方法显著地改变了成像振幅.为了更清楚地进行对比,下面抽取各种方法在CDP号为300位置处的单道成像结果进行对比,如图10所示.由图10可以看出,常规相关方法由于在反射层之上受到低频背景噪音的影响,其成像振幅小于零.Laplacian滤波方法和本文方法的结果在反射层之上的成像振幅趋近于零,由此可以看出它们都较好地实现了噪音的消除.但是进一步对比成像子波可以发现,本文波场分解方法的成像子波与相关方法更好地贴合,而Laplacian滤波方法的成像子波能量则存在显著差异.由此可以看出本文方法在成像子波保真性方面具有较好的表现.

图10 不同成像结果的单道对比(红色代表相关成像结果;绿色代表Laplacian滤波结果;蓝色代表波场方向分解结果)Fig.10 Trace comparison of imaging result from different methods

图11 实际数据偏移速度模型Fig.11 Migration velocity model of real data
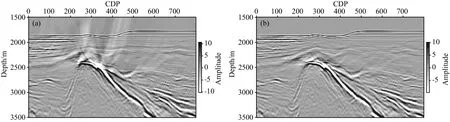
图12 实际数据成像结果对比(a) 传统逆时偏移结果; (b) 波场分离成像结果.Fig.12 Imaging results comparison of real data(a) Result of conventional RTM; (b) Result of wavefield separation.
下面采用某地区实际数据进行方法测试,偏移采用的速度模型为层析速度反演结果,如图11所示.在速度模型中可以看出较强的速度分界面,因此在常规逆时偏移结果(如图12a)上存在较强的低频噪音.采用本文方法提取炮点下行和检波点上行成像,炮点上行和检波点下行成像的结果,如图12b所示.由图可以看出,低频噪音得到了很好的消除,同时产生低频噪音区域的构造更加清楚.
5 结论
有效的炮点及检波点波场分解及相应波场的相关成像是高质量逆时深度偏移的核心.本文提出了解析时间波场外推及波场分解方法,能够在逆时深度偏移外推过程中的每个时间片上仅应用空间傅里叶变换实现波传播方向的有效分解,进而实现相应波场的相关成像,得到高质量的逆时深度偏移成像结果,低频噪音和成像假象被有效压制.相比于频率波数域波场分离方法,该方法具有较高的实现效率,与常规的相关+低频滤波的逆时深度偏移方法相比,增加的计算量较少.当然,该方法也可以应用于方位角度成像道集的生成,为后续的基于逆时深度偏移的速度层析反演和AVA分析与反演提供高质量的工具.
Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration.Geophysics, 48(11): 1514-1524.
Du Q Z, Zhu Y T, Zhang M Q, et al. 2013. A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration.ChineseJ.Geophys. (in Chinese), 56(7): 2391-2401, doi: 10.6038/cjg20130725.Fei T W, Luo Y, Aramco S, et al. 2010. De-blending reverse-time migration. ∥SEG Expanded Abstracts, 3130-3134.
Fei T W, Luo Y, Qin F H. 2014. An endemic problem in reverse-time migration. ∥SEG Expanded Abstracts, 3811-3815.
Fletcher R P, Fowler P J, Kitchenside P, et al. 2006. Suppressing unwanted internal reflections in prestack reverse-time migration.Geophysics, 71(6): E79-E82.Guitton A, Kaelin B, Biondi B. 2007. Least-squares attenuation of reverse-time migration artifacts.Geophysics, 72(1): S19-S23.
Kang W, Cheng J B. 2012. Methods of suppressing artifacts in prestack reverse time migration.ProgressinGeophys. (in Chinese), 27(3): 1163-1172.Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU.ChineseJ.Geophys. (in Chinese), 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.
Liu F Q, Hanson D W, Whitmore N D, et al. 2006. Toward a unified analysis for source plane-wave migration.Geophysics, 71(4): S129-S139.
Liu F Q, Zhang G Q, Morton S A, et al. 2007. Reverse-time migration using one-way wavefield imaging condition. ∥SEG Expanded Abstracts, 26: 2170-2174.
Liu F Q, Zhang G Q, Morton S A, et al. 2011. An effective imaging condition for reverse-time migration using wavefield decomposition.Geophysics, 76(1): S29-S39.
Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation.ChineseJ.Geophys. (in Chinese), 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024.
Liu S W, Wang H Z, Chen S C, et al. 2013. Implementation strategy of 3D reverse time migration on GPU/CPU clusters.ChineseJ.Geophys. (in Chinese), 56(10): 3487-3496, doi: 10.6038/cjg20131023.
Loewenthal D, Stoffa P L, Faria E L. 1987. Suppressing the unwanted reflections of the full wave equation.Geophysics, 52
(7): 1007-1012.
McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values.GeophysicalProspecting, 31(3): 413-420.
Whitmore N D. 1983. Iterative depth migration by backward time propagation. ∥SEG Expanded Abstracts, 382-385.
Yoon K, Marfurt K J. 2006. Reverse-time migration using the Poynting vector.ExplorationGeophysics, 37(1): 102-107.
Zhang Y, Sun J. 2009. Practical issues in reverse time migration: true amplitude gathers, noise removal and harmonic source encoding.FirstBreak, 26(1): 29-35.
附中文参考文献
杜启振, 朱钇同, 张明强等. 2013. 叠前逆时深度偏移低频噪声压制策略研究. 地球物理学报, 56(7): 2391-2401, doi: 10.6038/cjg20130725.
康玮, 程玖兵. 2012. 叠前逆时偏移假象去除方法. 地球物理学进展, 27(3): 1163-1172, 10.6038/j.issn.1004-2903.2012.03.041.
李博, 刘红伟, 刘国峰等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报, 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.
刘红伟, 李博, 刘洪等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报, 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024.
刘守伟, 王华忠, 陈生昌等. 2013. 三维逆时偏移GPU/CPU机群实现方案研究. 地球物理学报, 56(10): 3487-3496, doi: 10.6038/cjg20131023.
(本文编辑 胡素芳)
Reverse time migration using analytical time wavefield extrapolation and separation
HU Jiang-Tao, WANG Hua-Zhong
WPI,SchoolofOceanandEarthScience,TongjiUniversity,Shanghai200092,China
Two-way wave equation based reverse time migration is powerful in imaging complex area. However, its result usually contains imaging noise which poses challenge to seismic interpretation. The imaging amplitude would be distorted by simple noise filter. Wavefield separation imaging condition is an effective way to suppress the imaging noise and enhance the imaging quality. Conventionally, the wavefield separation is achieved in frequency wavenumber domain which cannot be conveniently implemented in time domain reverse time migration. We propose the analytical wavefield extrapolation method which can efficiently separate wavefield into its directional components during the time domain extrapolation. We use this method in reverse time migration and separate both the source and receiver wavefield. And the imaging noise and signal can be separated after applying the imaging condition to the separated wavefield.The wavefield propagation direction is usually defined by temporal and spatial Fourier transform. In the Fourier domain, the wavefield propagation direction is defined by the sign of frequency and spatial wavenumber. In order to efficiently apply the wavefield separation imaging condition in reverse time migration, we extend the analytical time signal into the wavefield and call it analytical time wavefield. Since the analytical time wavefield contains only the positive frequency component, the wavefield propagation direction can be defined by the sign of spatial wavenumber. To avoid the I/O cost in generating the analytical wavefield at every imaging point, we propose an analytical wavefield propagation equation based on the linear relation between the source term and wavefield in wave equation. We solve the proposed equation by finite difference method. Then we separate the source and receiver wavefield into their up and down going components and apply the imaging condition to the separated wavefield. Four imaging components (i.e., imaging component from up going source and down going receiver wavefield, imaging component from down going source and down going receiver wavefield, imaging component from down going source and up going receiver wavefield and imaging component from up going source and up going receiver wavefield) are effectively separated. Then the imaging noise and signal are separated.We use the syncline model and real data to test the proposed method. Numerical example on syncline model shows that the proposed method can effectively separate imaging component from down going source and up going receiver wavefield, imaging component from up going source and down going receiver wavefield, imaging component from down going source and down going receiver wavefield and imaging component from up going source and up going receiver wavefield. When the migration velocity is not accurate, the correlation imaging condition and equivalent wavefield separation imaging condition would generate imaging artifact in central area of the syncline. And the proposed method can eliminate the artifact. Numerical example on real data shows that this method can generate imaging result free from low frequency noise.Wavefield separation imaging condition can effectively separate the imaging noise and signal in reverse time migration and enhance the imaging quality. The proposed analytical wavefield extrapolation method can separate the source and receiver wavefield into their up and down going components. The imaging noise can be suppressed by applying the imaging condition to the separated wavefield. We want to further use this method to generate common angle imaging gather in reverse time migration and provide input data for AVA and migration velocity inversion.
Analytical time wavefield extrapolation; Wavefield separation; Noise elimination; Reverse time migration
973项目(2011CB201002),国家自然科学基金(41374117)以及国家重大专项(2011ZX05005-005-008HZ,2011ZX05006-002,2011ZX05023)资助.
胡江涛,男,1987年生,博士研究生,主要研究方向为地震波传播与成像方法及应用.E-mail:huidaojiaxiang@126.com
10.6038/cjg20150822.
10.6038/cjg20150822
P631
2015-01-08,2015-07-22收修定稿
胡江涛, 王华忠.2015.基于解析时间波场外推与波场分解的逆时偏移方法研究.地球物理学报,58(8):2886-2895,
Hu J T, Wang H Z. 2015. Reverse time migration using analytical time wavefield extrapolation and separation.ChineseJ.Geophys. (in Chinese),58(8):2886-2895,doi:10.6038/cjg20150822.

