结合LT码的自适应解调最优解调门限的研究

郭旭静

（湖南邮电职业技术学院，湖南长沙410015）

结合LT码的自适应解调最优解调门限的研究

郭旭静

（湖南邮电职业技术学院，湖南长沙410015）

【摘要】自适应解调是一种新的传输速率自适应方案，一般都需要结合无率码来使用，以解决解调中的比特删除问题。一种自适应解调方案是计算已调制符号中比特的对数似然比，与预设的解调门限相比较来决定是否解调该比特。解调门限决定了调制的阶数，并对无率码的译码性能有较大影响。文章对结合LT码的自适应解调中解调门限的设置进行研究，找到最优的解调门限。仿真结果表明，在最优门限下，可获得最低的误码率，或者获得最高的传输效率。

【关键词】LT码;自适应解调;最大后验概率;对数似然比;最优解调门限

自适应编码调制[1-2]（adaptive coding and modulation，AMC）是目前研究较多的速率自适应系统。在自适应编码调制系统中，发送端根据信道状态信息(channel state information, CSI)动态地改变编码和调制方式，在保证一定的传输可靠性下尽可能地提高频谱利用效率。在自适应编码调制系统中，接收端需要向发送端反馈信道状态信息，增加了发送端和接收端的复杂度和开销。另外一种速率自适应方式是结合无率编码（Rateless code）的自适应解调。2006年J. David Brown首先提出一种高斯信道下的自适应解调方案[3]，该方案是计算接收符号中每个比特的对数似然比(log-likelihood ratio，LLR)，将其从大到小排序，然后根据二元复合假设校验建立β-决策区域来选择接收符号中的β个可靠性最高的比特解调。仿真表明该方案可以减少系统开销，明显提高了系统的BER性能。但是该方案需要根据各比特的对数似然比划分决策区域，增加了系统复杂度。文献[4]提出了另一种自适应解调方案,该方案计算接收到的符号中每个比特的对数似然比，与预设的门限值比较，大于该门限的比特解调，否则删除。和文献[3]相比，虽然都是基于比特的对数似然比进行解调，但是文献[4]的算法复杂度明显降低，系统的BER性能提高。文献[5]在[4]的基础上进一步分析高斯信道下系统在不同信噪比下的BER，以及解调比例与解调门限间的关系。

上述两种自适应解调方案都需要使用无率码[6-7](Rateless Code)。在自适应解调过程中，删除了一些比特，如果重传这些删除的比特将会严重增加发送和接收端的复杂度。无率码与传统固定码率编码方式最大

的不同在于编码器不设定固定码率。编码器可以源源不断的产生编码数据，译码器接收到足够的编码数据后就可译码。在自适应调制系统中使用无率码就可解决解调中的比特删除问题。目前实用的无率码有LT 码[8]、Raptor码等[9]。在文献[3][4][5]的分析和仿真中，使用了LT码。

文献[4][5]是根据预设的解调比例确定解调门限，并分析了不同解调比例下的解调后的误码率。但它们都没有考虑门限的设置对无率码译码的影响。在某个特定的信噪比下，当解调门限设置较低时，会有较多的低似然比进入无率码的译码器。似然比低意味可靠度低。可靠度低的比特进入译码器后，有可能给译码器带来有用的信息，但更有可能带来的是有害的信息。而门限较高时，删除的比特较多，保留下来的比特可靠性较高。比特删除后需要发送端发送新的编码数据来弥补，使译码器能成功译码。门限解调门限设置过高，删除的比特过大，传输效率反而会下降。因此，在某个特定的信噪比下，一定存在一个最优的解调门限，在满足特定的传输质量要求时传输效率最高。针对这一问题，本文通过计算机仿真的方式对自适应解调中的解调门限设置对LT码的译码性能的影响进行分析，找出不同信噪比下的最优解调门限。

1　LT码编译码简介

LT码最初设计是应用在数据链路层，以包为单位进行传输，由于数据包内加有校验码进行差错校验，如果接收端检查出错误，就把该数据包删除，接收端继续接收新的数据包，只要接收够足够的数据包就可以正确译码，所以此时的LT码是作为纠删码使用。很多文献也把LT码作为纠错编码在物理层使用。在物理层喷泉码以比特数据流方式进行传输，由于噪声的加入，接收端收到的比特有可能是错误的，接收端收到足够的数据后，通过适当的译码方法，可把错误的比特纠正过来，此时喷泉码是作为纠错码。一类比较重要的消息传递算法称作置信传播算法[10](Belief Propagation Algorithm, BP算法)。置信传播算法本质上是一种迭代译码算法（Iterative Algorithms）,也被称作和积译码算法（Sum-Product Algorithm）。在该算法中，各个节点之间传递的信息是概率或置信信息，其消息需要在变量节点和校验节点之间传递。通过对接收信号所携带的信息进行多次的循环迭代，恢复出原始信息。

1.1LT码作为纠删码的编译码方法

LT码作为纠删码时，以数据包形式传输。编码时，先将信息按K个数据包为一组进行分组，编码器按某种度分布ρ(d)产生一个随机的度d，然后随机地从K个源数据包中选择d个数据包进行异或运算，得到一个编码数据包。这个过程可以一直持续下去，因此可不断产生编码数据包。

LT码的译码机制是：

1）接收端在接收到的编码数据包中寻找一个仅与一个源数据包(设为bk)关联的编码数据包tk，如果没有找到，则继续接收数据包。

2）然后令bk=tk。

3）将所有与bk关联的编码数据包与bk做模2加，即并将其与bk的关联关系移除。

4）在剔除tk后的编码数据包中重复第1～3步，直到译出K个源数据包。

1.2LT码作为纠错码的编译码方法

LT码作为纠错码时编码方式和作为纠删码时的相同，只是源信息以比特数据流形式传输。由于当LT码作为纠错码时，不能判断进入译码器的比特是否正确，只有似然比信息指示其可靠度，所以其译码采用软判决。

假设发送端发送的信息比特为u=(u1,u2…ui...)，接收端收到的信号为r= (r1,r2…ri.),Lr表示接收信号r的似然比信息。图1和图2通过Tanner图描述消息迭代过程。定义Lh(i,j)表示从信息比特i传递给编码比特j的似然信息(即概率)，Lt(i,j)表示从编码比特i传递给信息比特j的似然比信息。di表示与编码比特i相连的信息比特的数目，Ni表示与编码比特i相连的信息比特的集合；同理，li表示与信息比特i相连的编码比特的数目，ξi表示与信息比特相连的编码比特的集合。LT码作为纠错码的译码采用软判决，其译码过程如下：

图1　信息比特向编码比特的信息传递过程

图2　编码比特向信息比特的信息传递过程

1）在首次迭代时，Lh(i,j)和Lt(i,j)置零。消息迭代从度数为1的编码比特开始，度数为1的编码比特将其携带的似然比信息传递给与其相连的信息比特，然后信息比特i将与其相连的编码比特(不含编码比特j)的似然比信息按照公式(1)计算后的似然比信息传递给编码比特j，消息传递过程如图1所示：

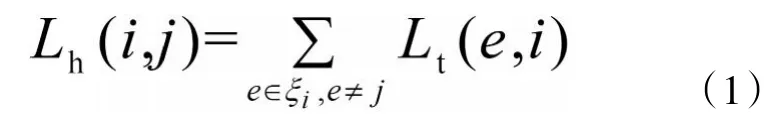
2）从编码比特向信息比特的消息传递过程如图2所示。编码比特i将其携带的似然比信息和与其相连的信息比特(不含信息比特j)的似然比信息按照公式(2)进行计算后的似然比信息传递信息比特j。随着迭代的进行，消息逐渐“覆盖”到所有边。

3）每次迭代结束后对所有信息比特依照(3)式计算L(ui)并做硬判决，判决规则为L(ui)>0,判为0，否则判为1，直到信息比特的信息被正确译出，否则继续迭代至最大迭代次数。

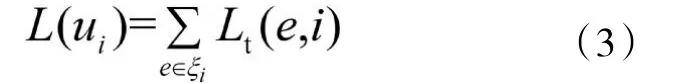
2　自适应解调方案

在自适应解调系统中发送端固定调制方式，接收端根据信道状态信息进行解调，解调比特多就是高阶调制，解调比特少就是低阶调制。发送端调制的阶数由信道的最好状态决定，阶数越高适应能力越强，但调制和解调的复杂度也越高。下面以16QAM为例介绍自适应解调的原理。

图3　16QAM的星座图

设调制符号为sk，其携带的四个信息比特为(b1k, b2k,b3k,b4k)。经过高斯信道传输后接收符号为rk,符号中每个比特bik的对数似然比为[5]：

假设采用如图3所示的16QAM星座，每个星座点选取的概率是相等的。接收符号中的每个比特的对数似然比为：

在自适应解调算法中，系统要预先设置一个解调门限L，然后将比特的对数似然比信息与该解调门限L相比较，L值的大小决定了解调的比特数，从而决定了调制的阶数。因此解调门限的设定对无率码的译码有较大影响，也决定着系统的性能。若解调门限设置过小，解调之后进入译码器的比特数较多，但有些比特携带的对数似然比信息对译码不利，反而会带来错误信息，使译码出来的信息错误率上升；然而，如果解调门限设置的过大，经过解调器时，就会有较多对数似然比没达到解调门限的比特被删除，从而进入译码器的信息比特也随之减少，导致接收端没有足够的编码比特参与无率码的译码，从而系统不能正确译码，误比特率较高，由无率码的特性可知，接收端就需要接收更多的信息比特才能使得译码成功，码率增大。

3　解调门限的仿真分析

由于比特的对数似然比信息表征了该比特为0/1的概率，由(5)式可知，若(5)式绝对值越大，则该比特携带的信息越可靠。我们用MATLAB仿真了高斯信道下接收符号中各比特对数似然比绝对值的平均值随信噪比的变化情况如图4所示，信息比特的长度K=1000。图中纵坐标为各比特对数似然比的绝对值的平均。由图可以看出，信噪比越大，接收符号中各比特的可靠度越高。

图4　不同信噪比下比特的对数似然比绝对平均值变化情况

由于解调门限的设定对无率码的译码有较大影响，决定着系统的性能。图5为码率为1/3时不同解调门限下的BER的仿真，由图可以看出，在不同的信噪比下若解调门限为固定的某个值，系统的BER性能并不是最优。所以本文以下部分将致力于寻找不同信噪比下的最优解调门限，从而使得该门限下系统的误比特率最低。

图5　不同解调门限下的BER

图6为在LT码的码率固定为1/3时，符号信噪比为10dB时，解调门限不同时LT码译码后的误比特率的仿真结果。仿真中，源信息分组长度为K=1000bit。由仿真结果可以看到，当解调门限L=5.5时，译码的误比特率最低，而大于或小于5.5误比特率都要上升，证明了我们的推断是正确的。最优的检测门限与接收信噪比有关。我们通过计算机仿真的方式对不同信噪比下、R=1/3时使LT码译码后的误比特率最小的解调门限，如图7所示。可以看到，信噪比越高，解调门限越高。这是因为随着信噪比的增大，由图(3)可知比特的对数似然比绝对平均值增大，所以达到最低误比特率时的解调门限就越高。

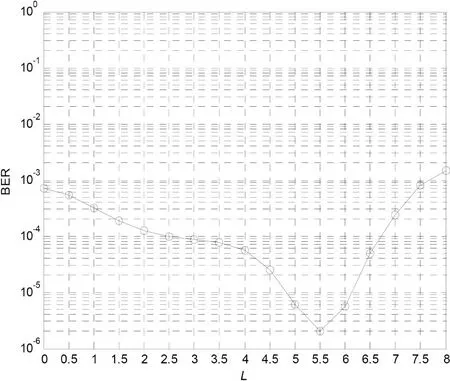
图6　Es/N0=10dB时不同门限下的BER值

图7　码率为1/3时不同信噪比下使得BER最小的最优门限

图8为不同信噪比时系统都采用自适应解调，在最优门限下和没有进行自适应解调，只级联了LT码的BER曲线，由图可以看出，采用最优解调门限时系统的误比特率明显降低。

图8　不同信噪比下的BER

自适应解调的最佳门限与LT码的码率设置有关，但在实际应用中LT码的码率是不固定的，而是根据信道情况自适应变化。此时，自适应解调门限的设置影响的是达到某个要求的译码误码率时发送端发送的数据量，也就是LT码的实际码率。图9是符号信噪比为12 dB时，以最终译码误比特率达到10-4为目标，不同解调门限时，达到目标误码率时实际的LT的码率。与码率固定时类似，这里也存在一个最优的解调门限Lo=2，使编码码率最大，传输效率最高。

我们采用计算机搜索的方式，以译码误比特率达到10-4为目标参数，寻找不同信噪比下使传输效率最高的最佳解调门限值，如图10所示。

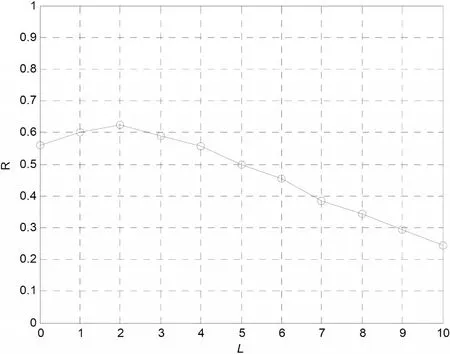
图9　Es/N0=12dB时不同门限下的码率

图10　不同信噪比下使得码率最大的最优解调门限

由图10可以看出，随着信噪比的增大，使得码率最大的最优门限也增大，这是因为随着信噪比的增大，各调制符号中比特的对数似然比的绝对值的平均值增大，在保证一定误码率的目标参数时，最优的解调门限固然也随着增大。

4　总结

自适应解调是一种新的速率自适应传输方案，接收端计算各符号中比特的对数似然比，并与预设的门限相比较，大于该门限就解调，否则删除。因此解调门限是自适应解调系统中的关键参数，对系统的性能有较大的影响。本文分析了解调门限对LT码译码的影响，并通过计算机仿真搜索了LT码固定码率、不固定码率两种情况下的最佳解调门限。该门限与接收信噪比有关。依据最佳门限进行自适应解调，可使系统性能最佳。

【参考文献】

[1] Webb W T, Steele R. Variable rate QAM for mobile radio [J]. IEEE Transactions on Communications, 1995, 43(7): 2223-2230.

[2] Goldsmith A J, Chua S. Variable-rate variable power MQAM for fading channels [J]. IEEE Transactions on Communications, 1997, 45(10): 1218-1230.

[3] Brown J D. Adaptive Demodulation Using Rateless Erasure Codes[J]. IEEE Transactions on Communications, 2006, 54 (9): 1574-1585.

[4] Kadir Turk, Pingyi Fan. Adaptive Demodulation Using Rateless Codes Based On Maximum a Posteriori Probability [J]. IEEE Communications Letters, 2012, 16(8)：1284-1287.

[5] Yuheng Huang, Yan Dong, Rupeng Xie. A New Rate Adaptive System: Controlled Soft Demodulation[C]. Computing, Communications and Applications Conference, 2012.360-364.

[6] MacKay D. J. C. Fountain codes[C]. Proceeding of IEE Communication, 2005, 152(6): 1062- 1068.

[7] Mitzenmacher M. Digital fountain: a survey and look forward [C]. IEEE Information Theory Workshop, 2004.271-276.

[8] Luby M. LT codes[C]. Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002. 271-280.

[9] Shokrollahi A. Raptor Codes [J]. IEEE Transactio- ns on Information Theory, 2006, 52 (6): 2551-2567.

[10] Stockhammer T, Jenkac H, Mayer T, et al. Soft decoding of LT-codes for wireless broadcast [A]. Proc. IST Mobile[C]. 2005.

Research on optimal demodulation threshold of adaptive demodulation combined with LT codes

GUO Xu-jing
(Hunan Post and Telecommunication College, Changsha, Hunan, China 410015)

Abstract：Adaptive demodulation is a new rate-adaptive scheme and it always applies with rateless code so as to solve problem of the delete bits. An adaptive demodulation scheme computes the log-likelihood ratio of each bit in the modulated symbol, then compares with the pre-set threshold to determine whether to demodulate this bit or not. The demodulate threshold in this algorithm determines the demodulation order, so the threshold has great influence on the decoding performance. This paper studies the demodulation threshold of this adaptive demodulation algorithm combined with LT code, and finds out the optimal threshold. Simulation results indicate that, at optimal thresholds, system can obtain lowest bit-error-ratio, or best transmission efficiency.

Keywords：LT code; adaptive demodulation; maximum posteriori probability; LLR; optimal demodulation threshold

[作者简介]郭旭静（1988-），女，河南南阳人，助教，硕士，研究方向：移动通信技术。

[收稿日期]2015-09-29

【中图分类号】TN919.3

【文献标识码】A

【文章编号】2095-7661（2015）04-0033-05

【doi:10.3969/j.issn.2095-7661.2015.04.009】