河西走廊西部夏季降水发生概率时空变化的隐马尔科夫模型分析

彭 俊，董治宝，韩凤清

（1.中国科学院寒区旱区环境与工程研究所，兰州 730000；

2.中国科学院青海盐湖研究所，西宁 810008）

doi：10.7515/JEE201505004

河西走廊西部夏季降水发生概率时空变化的隐马尔科夫模型分析

彭 俊1，董治宝1，韩凤清2

（1.中国科学院寒区旱区环境与工程研究所，兰州 730000；

2.中国科学院青海盐湖研究所，西宁 810008）

使用隐马尔科夫模型分析了河西走廊西部地区5个站点1955—2013年共59年的夏季逐日降水数据。结果表明4个隐状态能较好地描述研究区域的夏季日降水发生模式，状态1与2描述的区域环流特征区分了地理位置对日降水模式的影响，状态3与4表征了大尺度大气环流模式下5个站点同时下雨或都不下雨的情形。5个站点的日降水模式存在显著性的区域差异，日降水发生概率呈由东向西逐渐减小的趋势。隐状态的年际变化分析表明，所有站点（包括西部站点）的降水发生概率都存在增加趋势，东部站点湿润而西部站点干燥的情景呈显著性减少趋势，这可能与全球变暖导致的夏季风北移使该区域不同站点降水模式趋于一致有关，其原因有待进一步研究。

河西走廊；夏季降水；隐马尔科夫模型

河西走廊地区降水稀少，年降水量仅为40～400mm，年蒸发量高达1500～3000mm，属于典型的内陆性干旱气候。降水资源作为制约该地区人类生产活动的基本要素，对该地区生态环境变化起决定性作用，开展降水变化规律研究对揭示该地区的水资源分布特征与规律，开展干旱区生态建设及水资源保护与合理利用均具有重要意义。近年来，国内研究者对河西走廊地区气候变化开展了广泛的研究。施雅风等（2003）指出，西北地区西部降水自1970年中期开始增加，并在1987年发生了向暖湿型的突变，气候呈变暖变湿趋势的地区包括祁连山、河西走廊中西部及青海部分地区等。李栋梁等（2003）对西北地区气候变化的研究表明，该地区气候正逐渐由暖干向暖湿转变，这种转变在西北西部地区包括新疆、河西走廊西部、祁连山与青海部分地区表现明显。孟秀敬等（2012）分析了河西走廊近57年来的气温 与降水变化，认为河西走廊降水量呈增加趋势，但区域差异明显，其中黑河流域东部与石羊河流域变化相似，而黑河流域中西部与疏勒河流域降水变化较为一致，作者认为这种差异与该地区季风环流及局部地理差异有关。蓝永超等（2012）分析了近50年来河西走廊西部疏勒河流域山区的气象数据，认为受全球气候变暖影响，疏勒河山区气候持续向暖湿化转变，山区降水量总体上呈增加趋势。上述研究者在气候变化研究中多采用趋势分析（如滑动平均、线性回归等）、突变分析（如Mann-Kendall、累积距平等）等统计方法，分析采用的数据主要为不同气象站的年/月均降水数据，研究重点为降水序列的年际变化特征，而较少关注对基于逐日降水数据的日降水发生模式及其变化特征的分析。

在日降水发生模式分析方面，近年来应用较普遍的一种方法是隐马尔科夫模型。隐马尔科夫模型（HMM：Hidden Markov Model）是一种含隐状态的马尔科夫过程，被广泛地应用于时间序列数据模拟与预测（Zucchini and MacDonald，2009）。Zucchini and Guttorp（1991）提出使用HMM模拟多站点降水过程的方法，并首次使用该方法研究了同一区域多站点的日降水发生模式。HMM在多站点降水过程模拟中的优点在于可通过概率模型识别出表征降水发生模式的隐状态，将单个站点降水发生的自相关与多站点降水变化的空间相关联系起来。Robertson et al（2004）利用HMM分析了巴西东北部地区2—4月份的日降水发生概率，识别出4种表征降水空间变化特征的隐状态，作者认为其中一些隐状态与热带辐合带的移动、厄尔尼诺-南方涛动、及北大西洋涛动现象有关。Pal et al（2014）利用HMM研究了印度西北部地区冬季的日降水过程，使用4个隐状态描述了该地区日降水空间变化特征，表明不同隐状态与不同的大气环流模式有关。本文使用来自中国气象数据中心的日降水数据，利用HMM分析了河西走廊西部地区5个站点1955—2013年夏季日降水数据，旨在揭示该地区夏季日降水发生模式与变化规律，为干旱区水资源的可持续开发利用提供科学依据。

1 数据与方法

1.1 数据处理

所使用的数据为来自河西走廊西部地区5个气象站（敦煌、瓜州、玉门、酒泉、鼎新，见图1）的1955—2013年逐日降水数据，数据下载自中国气象科学数据共享服务网（http：//cdc.nmic.cn/home.do）。用0—1值对逐日降水数据重新赋值：定义日降水量＜0.1mm的当天降水次数为0（无降水发生），日降水量≥0.1mm的当天降水次数为1（降水发生）。根据59年来月均降水数据的统计结果（图2），河西走廊西部地区降水集中发生在夏季（6、7、8月）。本文将对降水频次较集中月份的逐日降水数据进行分析，提取出5个站点的共59年的夏季92日（6月30天，7、8月各31天）逐日降水数据，总数据量为5×59×92=27140。

图1 河西走廊西部地区5个气象站的地理位置Fig.1 Locations of 5 stations in the western of Hexi Corridor

图2 1955—2013年5个站点的月均降水次数Fig.2 The mean seasonal variations of daily rainfall occurrence frequencies at 5 stations from 1955 to 2013

1.2 HMM简介

HMM为由观测序列及对应隐状态组成的一种双重随机过程，其不同于一般马尔科夫模型的特点在于观测数据的状态是隐而未知的，而不是已知或由人为主观规定的。对常见的一维数据结构，记n个观测数据的集合为X={X1，X2…Xn}（对于本文采用的二维观测数据，X={X1·，X2·…Xn·}），对应的n个隐状态集合为C={C1，C2…Cn}，HMM的两个基本假设为（Zucchini and MacDonald，2009）：

（1）当前状态仅由紧邻的前一个状态决定，即Pr（Ct/C）=Pr（Ct/Ct-1）；

（2）当前观测值仅由相应的隐状态决定，即Pr（Xt/X，C）=Pr（Xt/Ct）。

其中Xt表示t（t=1，2…n）时刻的观测值，Ct表示Xt对应的隐状态（图3）。不同隐状态间的一阶转移概率构成二维矩阵集合T={Pr（Ct=j/Ct-1= i）；i=1，2…m；j=1，2…m}，不同隐状态下观测值Xt出现的条件概率构成一维向量集合Pr（Xt/Ct）={Pr（Xt/Ct=i）；i=1，2…m}。

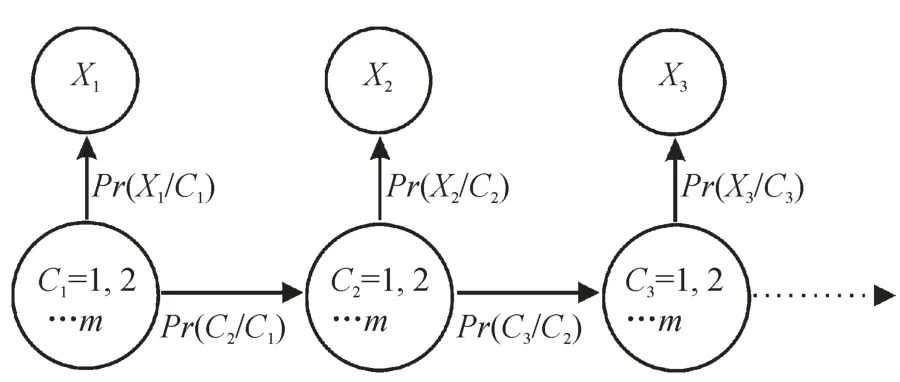
图3 HMM图示Fig.3 Directed graph of a Hidden Markov model

假定t时刻k个不同观测站的降水值相互独立且服从0—1分布（0表示无降雨，1表示降雨），则t时刻的观测值集合为Xt·={Xtj；j=1，2…k}，定义πij为状态i下第j个观测站的日降水概率，则t时刻给定隐状态i（Ct=i）下Xt·的条件概率可表示为：

定义δ为t=0时刻不同隐状态出现的初始概率，则Pr（C1）=δT为t=1时刻不同隐状态出现的边缘概率，观测值与隐状态的联合概率可表示为：

对公式（2）进行边缘化求和，消去观测序列X={X1·，X2·…Xn·}对应的隐状态序列C={C1，C2…Cn}可以得到观测序列的边缘概率：

公式（3）描述的模型中的待估参数包括：隐状态的初始概率δ={δi；i=1，2…m}，隐状态概率之和为1，故δ含m-1个自由参数；状态转移概率矩阵T={Pr（Ct=j/Ct-1=i）；i=1，2…m；j=1，2…m}，转移矩阵各行之和为1，故T的自由参数总数为m（m-1）；不同隐状态下各站点的日降水概率π={πij；i=1，2…m；j=1，2…k}，故π共有km个自由参数。模型参数总数为（m-1）+（m2-m）+ km，通常使用极大似然估计法来确定能使联合似然函数L最大的参数组合。

根据Zucchini and MacDonald （2009），定义观测序列t时刻隐状态i的向前概率（Forward probability）及向后概率（Backward probability）分别为：

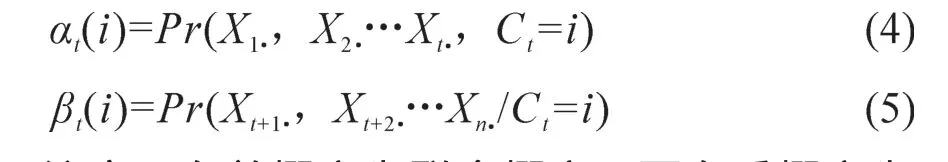
注意，向前概率为联合概率，而向后概率为条件概率。在确定了模型（3）的参数并由公式（4）与（5）计算出观测序列t时刻隐状态i的向前概率与向后概率后，便可计算t时刻观测值Xt·的隐状态Ct为i的条件概率：

利用公式（6）及模型优化的不同隐状态下各站点的日降水概率π，便可计算t时刻各站点日降水的条件概率（日期望降水次数）。如：πij为隐状态i下第j个观测站的日降水概率，则t时刻第j个观测站的日降水概率的条件分布为：

2 结果分析与讨论

2.1 模型训练与验证

使用1955—2004年共50年的逐日降水数据估计模型参数（模型训练），并利用其后9年的降水数据对模型参数估计的结果进行检验（模型验证）。本文使用HMM参数估计的期望最大化法（Baum—Welch算法）（Welch，2003）估计能使观测序列值的联合似然函数值L最大的参数组合（Kirshner，2005），由于期望最大化算法对初值敏感而易于陷入局部最优解，本文采用不同的初始参数多次优化取最优估计的方法来确定模型的最优解。HMM参数估计的另一个问题是关于隐状态数m的确定，一方面要保证模型有足够的拟合优度，另一方面不能因为状态数过多而发生冗余，造成模型的复杂度增加并给观测数据的解释带来困难。可使用贝叶斯信息准则（Schwarz，1978）来确定最佳隐状态的数目，贝叶斯信息值（BIC）综合考虑了模型的拟合优度和自由参数的数目，关于该方法在模型选择中的应用，可参考Peng et al（2014）。

图4为BIC值随隐状态数目的变化图，BIC值随隐状态数目的增加先减小后变大，状态数目为4时BIC值最小，由此可以确定隐状态的最佳个数为4。图5给出了不同站点1955—2004年夏季实际降水次数（黑线）与模型拟合的降水次数（蓝线）的对比，通过训练模型获得的各站点降水发生次数的期望值与实际观测值的变化趋势和幅度都较为一致。为了进一步验证模型参数估计的可靠性，利用2005—2013年共9年的降水数据对训练获得的模型进行验证，其结果见图6。根据模型训练获得的参数与独立的验证数据估计的2005—2013年降水期望次数（蓝线）和实际降水次数（黑线）非常相似，这说明根据历史降水数据训练确定的模型参数可以用来指导对未来降水变化的预测评估，进一步说明模型参数训练结果是可靠的。

图4 BIC值随隐状态数变化Fig.4 Variations of Bayesian Information Criterion score with the number of hidden states

2.2 隐状态特征分析

表1为模型估计的4种不同隐状态下各站点的夏季日降水概率分布。由表1可以看出，状态1下5个站点的降水概率呈由西向东逐渐减小的趋势，敦煌和瓜州具有较高的降水概率（均大于0.59），玉门居中（0.43），酒泉和鼎新的降水概率较低（均小于0.26）。状态2与状态1相反，日降水概率由西向东逐渐增加，敦煌和瓜州的降水概率均不足0.1，玉门为0.4，而酒泉和鼎新的降水概率都在0.65以上。状态3与状态4也呈现出相反的变化特点，状态3下所有5个站点的降水概率都很高（均大于0.8），意味着此状态下5个站点同时发生降水的可能性很大。相比之下，状态4下各站点的降水概率都极低（均小于0.05），代表所有站点都不发生降水的干燥状态。由以上分析可知，状态1与2代表的降水模式区别了不同站点的地理位置导致的夏季日降水发生模式的空间差异，而状态3与4代表的降水特征描述了大尺度气候环流控制下5个站点都发生降水或者都不发生降水的情形。研究区域内夏季不同站点受季风和大气环流影响的程度不同，我国夏季风西北边界在河西走廊中段武威—金昌—民勤一带（王宝鉴等，2004），酒泉和鼎新位于夏季风北界边缘，敦煌和瓜州地理位置更偏西，除受夏季风影响外，还受到明显的西风气流的影响（孟秀敬等，2012），由此造成日降水发生模式的东西向空间差异。

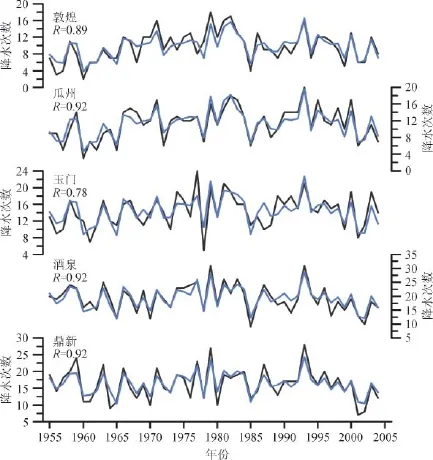
图5 不同站点1955—2004年夏季实际降水次数与模型拟合降水次数的比较Fig.5 Comparisons of the observed daily rainfall occurrence frequencies in summer with those f tted by the Hidden Markov model for various stations during 1955—2004

图6 不同站点2005—2013年夏季实际降水次数与期望降水次数的比较Fig.6 Comparisons of the observed daily rainfall occurrence frequencies in summer with those expected from the Hidden Markov model for different stations during 2005—2013

表2为模型估计的隐状态间的转移概率矩阵。最为稳定的状态是状态4，其向其他状态转变的概率都低于0.08，说明所有站点夏季日天气状况以干燥状态为主。最不稳定的是状态1，它向其他状态转变的概率均显著大于维持自身状态的概率，这表明同一天西部站点发生降水而东部站点不发生降水的情景较为罕见。状态2比状态3稍稳定，表明东部站点下雨而西部站点不下雨的概率高于所有站点都下雨的概率。状态2易于向状态4转变，这意味着假定今天仅东部站点发生降水，则明天所有站点都为干燥状态的可能性极大（概率约为0.63）。状态3易于向状态2或4转变，即若今日所有站点都发生降水，则明日很可能仅东部站点下雨或者所有站点都不下雨。

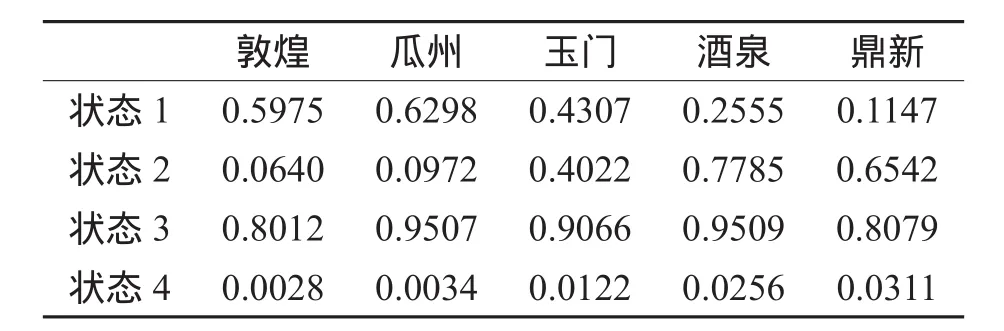
表1 各站点不同状态下的日降水概率矩阵πTab.1 Probabilities of daily rainfall occurrence for different stations under various hidden states

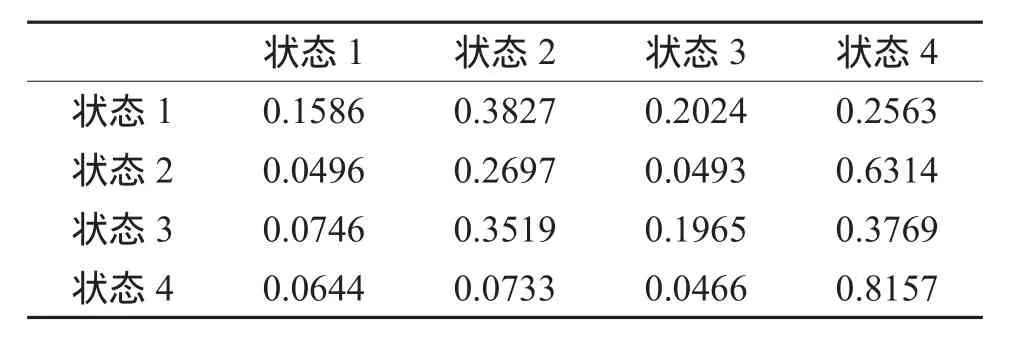
表2 不同隐状态间的转移概率矩阵TTab.2 Transition probabilities for the 4-state Hidden Markovmodel

为进一步揭示1955—2004年观测降水数据对应的隐状态随时间变化的规律，本文根据模型训练获得的参数组合，使用Viterbi算法（Viterbi，1967）估计与观测序列对应的逐日最优隐状态序列（见图7）。由图7可知，研究区域的日天气状况以干燥为主，其比重高达73.8%。不同状态的交互出现呈随机分布并无规律可循，且年际差别大，符合马尔科夫过程的随机特点。不同隐状态占总体比重关系为：状态4＞状态2＞状态3＞状态1，这与表2的估计结果是一致的。

根据图7的结果，可进一步计算不同隐状态出现的月平均次数（见图8）。图8的结果显示7月份状态4 出现的次数最少，而状态1、2、3出现的次数最多，这表明夏季降水发生最集中的月份为7月，此时夏季风输送到西北地区的气流最为深厚，易于致雨（姜旭与赵光平，2013）。

图7 Viterbi算法估计的逐日最优隐状态序列Fig.7 The optimal sequence of hidden states estimated using the Viterbi algorithm

图8 夏季不同月份 4种状态出现的平均次数Fig.8 The mean daily rainfall occurrence frequencies forvarious states in different months of summer

图9给出了1955—2004年间夏季不同隐状态出现总次数的变化趋势。Mann-Kendall 趋势分析计算的四种隐状态序列的tau值分别为 0.17、 - 0.19、0.11、0.02，即状态1、3出现的次数随年份略呈增加的趋势，状态2呈减少趋势，状态4增加不明显。4种状态在零假设为无明显趋势下（显著性水平为α=0.1）的双侧显著性检验p值分别为0.11、0.06、0.29、0.86，即状态1、3、4的增加趋势都不显著，而状态2的减少趋势是显著的。状态2呈显著减少趋势，说明东部站点下雨而西部站点不下雨的情景在逐渐减少。状态1与3的增加说明西部站点与所有站点的湿润状态都可能存在增加趋势，尽管趋势都不显著。这可能与夏季风增强推进有关，由全球变暖导致的太平洋副热带高压的增强有利于东亚夏季风向更西北方向推进（孟秀敬等，2012），使更大范围内的降水受夏季风控制，从而使不同地区夏季日降水模式之间的差异变小，造成区域内所有站点同时发生降水的情景增多，同时东部站点发生降水而西部站点不发生降水的情景减少。对近50年来河西走廊西部疏勒河流域山区的气候变化研究也表明，受全球变暖的影响，疏勒河地区气候持续向暖湿转化（蓝永超等，2012）。应该注意到，由于模型分析用到的观测数据有限，且时间序列的趋势分析结果对数据结构的变化很敏感，因此对这些有限量数据预测分析结果的解释要谨慎，基于HMM模型参数估计的讨论也只能是试探性的，今后尚需利用更长的序列数据做进一步研究。

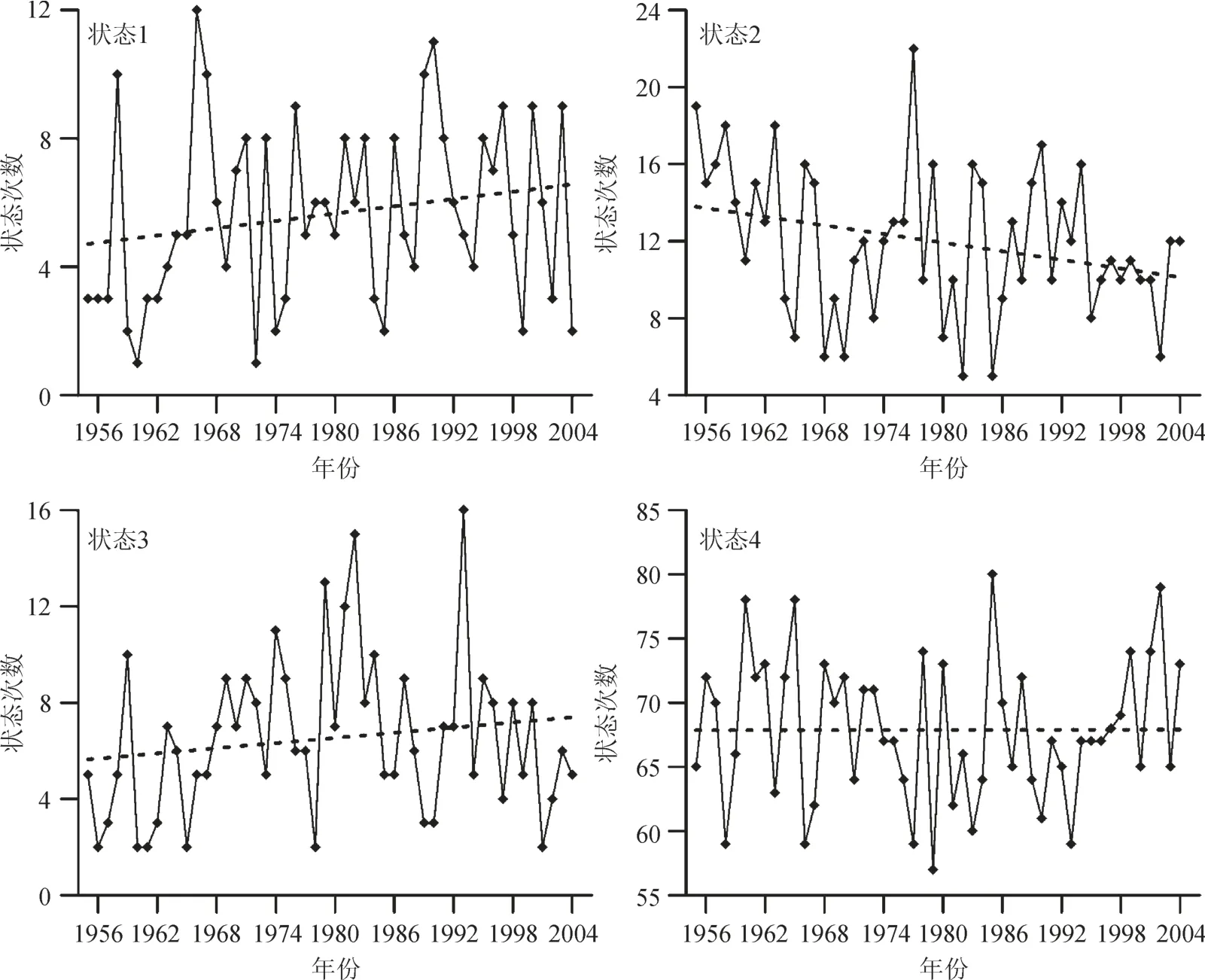
图9 1955—2004年4种隐状态出现次数的变化Fig.9 Variations of occurrence frequencies for various states from 1955—2004

3 结论

使用HMM对河西走廊西部5个站点的夏季日降水数据进行了分析。利用1955—2004年的降水数据对模型进行参数训练，并使用2005—2013年共9年的降水数据对模型参数训练结果进行检验。结果表明4个隐状态能较好地描述研究区域的夏季日降水发生模式，基于模型的期望降水次数与观测降水次数之间吻合较好。分析还表明，西部站点与所有站点的湿润状态发生概率（状态1与3）都存在增加趋势，同时东部站点湿润而西部站点干旱的情景（状态2）呈显著性减少趋势，这可能与全球变暖导致的夏季风北移有关。HMM较好地描述了小区域内多站点的降水发生概率及其时空变化特征，识别出了不同站点的日降水发生模式的东西向显著差异，对干旱区降水发生规律研究与变化趋势预测有一定的指导意义。

姜 旭，赵光平.2013.中国西北地区东部雨日的气候特征及其与低空风场的相关性研究 [J].中国沙漠，33（3）： 888 - 895.[Jiang X，Zhao G P.2013.The climatic character of precipitation days in the east of northwest China and the correlation between the precipitation days and low-level wind shear [J].Journal of Desert Research，33（3）： 888 - 895.]

蓝永超，胡兴林，肖生春，等.2012.近50年疏勒河流域山区的气候变化及其对出山径流的影响 [J].高原气象，31（6）： 1636 - 1644.[Lan Y C，Hu X L，Xiao S C，et al.2012.Study on climate change in mountainous region of Shulehe river basin in past 50 years and its effect to mountainous runoff [J].Plateau Meteorology，31（6）：1636 - 1644.]

李栋梁，魏 丽，蔡 英，等.2003.中国西北现代气候变化事实与未来趋势展望 [J].冰川冻土，25（2）： 135 - 142.[Li D L，Wei L，Cai Y，et al.2003.The present facts and the future tendency of the climate change in northwest China [J].Journal of Glaciology and Geocryology，25（2）：135 - 142.]

孟秀敬，张士锋，张永勇.2012.河西走廊57年来气温和降水时空变化特征 [J].地理学报，67（11）： 1482 - 1492.[Meng X J，Zhang S F，Zhang Y Y.2012.The temporal and spatial change of temperature and precipitation in Hexi corridor in recent 57 years [J].Acta Geographica Sinica，67（11）： 1482 - 1492.]

施雅风，沈永平，李栋梁，等.2003.中国西北气候由暖干向暖湿转型的特征和趋势探讨 [J].第四纪研究，23（2）：152 - 164.[Discussion on the present climatic change from warm-dry to warm-wet in northwest China [J].Quaternary Sciences，23（2）： 152 - 164.]

王宝鉴，黄玉霞，何金海，等.2004.东亚夏季风期间水汽输送与西北干旱的关系 [J].高原气象，23（6）： 912 - 918.[Wang B J，Huang Y X，He J H，et al.2004.Relation between vapour transportation in the period of east Asian summer monsoon and drought in northwest China [J].Plateau Meteorology，23（6）： 912 - 918.]

Kirshner S.2005.Modeling of multivariate time series using hidden Markov models [D].Irvine City： University of California.

Pal I，Robertson A W，Lall U，et al.2014.Modeling winter rainfall in Northwest India using a hidden Markov model：understanding occurrence of different states and their dynamical connections [J].Climate Dynamics，44（3 - 4）：1003 - 1015.

Peng J，Dong Z B，Han F Q，et al.2014.Estimating the number of components in an OSL decay curve using the Bayesian Information Criterion [J].Geochronometria，41（4）：334 - 341.

Robertson A W，Kirshner S，Smyth P.2004.Downscaling of daily rainfall occurrence over Northeast Brazil using a Hidden Markov Model [J].Journal of Climate，17：4407 - 4424.

Schwarz G.1978.Estimating the dimension of a model [J].Annals of Statistics，6（2）： 461 - 464.

Viterbi A J.1967.Error bounds for convolutional codes and an asymptotically optimum decoding algorithm [J].IEEE Transactions on Information Theory，13（2）： 260 - 269.

Welch L R.2003.Hidden Markov models and the Baum-Welch algorithm [J].IEEE Information Theory Society Newsletter，53（4）： 10 - 13.

Zucchini W，Guttorp P.1991.A hidden Markov model for space-time precipitation [J].Water Resource Research，27（8）： 1917 - 1923.

Zucchini W，MacDonald I L.2009.Hidden Markov Models for Time Series： An Introduction Using R [M].London：Chapman and Hall Press，45 - 87.

Analyzing the time-space variation of daily rainfall occurrence during summer in the western of Hexi Corridor using a Hidden Markov model

PENG Jun1，DONG Zhi-bao1，HAN Feng-qing2
（1.Cold and Arid Regions Environmental and Engineering Research Institute，Chinese Academy of Sciences，Lanzhou 730000，China; 2.Qinghai Institute of Salt Lakes，Chinese Academy of Sciences，Xining 810008，China）

Daily rainfall data during the June—August 1955—2013 from 5 stations located in the western of Hexi Corridor was analyzed using a Hidden Markov model（HMM）.The result indicates that a four-state HMM is able to capture the patterns of variations in daily rainfall probability for the 5 stations.One paired states（states 1 and 2）describe zonal circulation patterns and demonstrate the inf uence of geographical location on the pattern of daily rainfall occurrence while a second paired of states（states 3 and 4）describe dry-versus-wet conditions at all stations that are controlled by the largescale circulation of atmosphere.Difference in summer rainfall pattern is characterized by signif cant east-west gradients in rainfall occurrence probability.Increase in states 1 and 3 and a significant decrease in state 2 are identif ed，which implicates that the occurrence probabilities of summer daily rainfall in the 5 stations are increased and become uniform.This may be caused by the fact that the northward-moving of Summer Monsoon triggered by the global warming results in a more uniform circulation pattern over the studied area.The responsibility for this phenomenon deserves a further study.

Hexi Corridor; rainfall in summer; Hidden Markov model

O211.62；P426.6

A

1674-9901（2015）05-0283-08

2015-07-15

国家重大科学研究计划项目（2013CB956000，2012CB426501）

彭 俊，E-mail： pengjun10@mails.ucas.ac.cn