考虑易逝品的流通时间增加对供求双方博弈的影响

何朋飞， 郭 彪，潘倩兰

(南京农业大学工学院管理工程系，江苏南京 210031)



考虑易逝品的流通时间增加对供求双方博弈的影响

何朋飞， 郭 彪*，潘倩兰

(南京农业大学工学院管理工程系，江苏南京 210031)

首先考虑到易逝品在二级供应链的流通过程存在各方利润比例分配不合理的状况，通过建立易逝品流通的利润博弈函数，对利润函数进行分析得出各方利润的最大的均衡条件。再者考虑易逝品的从属失效性，构建关于时间的易逝品损耗函数；将损耗函数与利润博弈函数相结合，分析随流通时间变化对各方在整条供应链上的利润比例的变化。结果表明，流通时间的增加需求方所占的利润比例逐渐向1靠拢；当流通时间接近易逝品的腐烂周期时，供应方所占的利润比例接近于0。

易逝品；博弈；流通时间；损耗函数；利润比例

结合南京市众彩物流的实地调研，通过走访当地农户以及对商贩进行座谈，发现目前南京及其周边地区农超对接的建立完善程度相对较低，农产品等易逝品的交易模式仍然处于较为落后的状态，虽然部分大型连锁超市已经开始建立这一供应模式，并取得初步成果，但在超市与农户的合作关系模式下就建立了二级供应链，在调研过程中发现二级供应链的供需双反在利润分配上存在较大差距。前人在此问题上做过相关研究，但止步于分析一个供应链的供需双方在均衡支付条件下的利润比例，没有切实的考虑到农产品在随着流通时间的增加其本身的价值正在进行减少，雷露等将这一种损失定义成为一种从属失效性[1]。笔者在前人研究的基础上建立斯坦克尔伯格博弈模型(即超市与农产品生产商的博弈模型)，把损耗函数与博弈模型结合在一起，这样的模型能够更加清晰地反映出农产品在流通过程中其价值的真实变化状况，因此在搭建整条供应链的利润函数和农产品的损耗函数的同时考虑到不同农产品的特性，在模型中通过调节参数变化可以得到农产品在流通过程中供应链利润变化的真实状况，且整条供应链存在唯一的利润最大化的均衡价格。笔者通过农产品的损耗函数随时间变化分析二级供应链的供需双方利润比例的变化，研究易逝农产品的损耗在非线性增长的情况下的农超双方的利润比例的变化情况，进而得出相关结论，提出能够保护农户即生产者在整条供应链上的利润比例。

1 研究综述

回顾近年来的文献，国内外众多学者进行了相关不同层次上的研究：Mousiter等对越南经营的蔬菜、荔枝的8个农民团体直接向超市供货案例的研究，探讨小规模的农户直接向超市供货这样一个二级供应链中农户组织发挥的作用[2]。Pritchard分析了农超对接对农村公社的影响，发现需求方与农户之间存在诸多不稳定因素[3]。Lau等通过建立零售商的斯坦克尔伯格博弈模型，分析了需求方在在生产方成本费用为不完美信息下，提出了相关的解决方案[4]。Christin Schipmann等以泰国甜椒为例，分析了农户对不同收购渠道的喜好程度，结果显示了农户更倾向于非合同的收购方式[5]。席其鲁等利用博弈论方法对只有农户和超市2个利益主体的农超对接基础模式进行研究分析[6]。刘欢欢等对农超对接模式中双方的利益进行博弈分析，找到纳什均衡点，分析发展农超对接模式的意义[7]。刘磊等运用合作博弈与非合作博弈理论来分析超市与合作社的博弈分析超市与合作社的博弈行为[8]。殷丽玲从合作博弈的农超对接利益分配问题出发，分析得出利益分配关键体现在农产品的价格上[9]。任向阳等利用博弈理论分析单一农户和单一超市在非合作和合作下的供应链总利润的差异，利用Shapley值法对合作供应链进行分配[10]。目前在应用经济学博弈模型分析供应链效益上存在部分相关文章，但始终存在的问题就是在分析二级供应链的供求双方的博弈过程中所占利润比例基本是一个静态的过程，并没有研究随着农产品流通时间的长短和农产品损耗程度的变化而引起均衡支付比例的变化方式和变化范围。笔者在前人研究的基础上，在农产品的二级供应链上结合斯坦克尔伯格博弈模型，增加和减少相关变量，并将农产随时间损耗的函数模型与上述模型结合在一起，建立了一个二级供应链上需求双方所占利润的比例随着时间变化改变的动态方程。由于农产品的易损耗的性质非常特别，不同种类的农产品的损耗随着时间的推移会有不同的损耗比例，因此笔者在参考相关损耗函数后，按照农产品的性质构建新的损耗函数，最终方程的结果会随着时间的改变而变化，得出不同性质的农产品随流通时间的不同需求双方所获得的供应链的利润比例会不同。

2 条件假设及变量说明

在供应链中二者都是利益相关者，2个主体之间既是竞争又是合作的关系，客观地存在利益冲突，又有风险分担的问题，因此解决供应链中农户和超市的利润比例是一个关键问题。该研究在供应链的均衡支付条件下分析了随着时间变化不同农产品的损耗对均衡支付比例产生的影响。

2.1 前提条件假设结合前人研究，针对该研究对象具体情况提出如下假设：

(1)模型中博弈双方都是有限理性理性和风险中性的。

(2)每一位参与人对于其他参与人的特征、策略空间以及支付函数都有准确的信息。

(3)时期内蔬菜的流通较为稳定，价格相对均衡。

(4)没有缺货情况，存货下降为0时自动补充货源。

(5)蔬菜的自然属性，在农户方面存在库存成本，但超市方面没有存货。

(6)蔬菜存在损耗，且损耗函数按照以为底的指数函数增加。

(7)考虑超市是与多个农户进行合作。

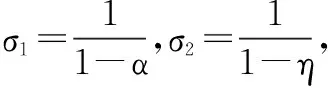
3 博弈模型分析

3.1 博弈模型的建立

3.1.1收益函数的建立。

供应商的收益函数：l1=(p1-c1σ1-c3σ1)q

需求方的收益函数：l2=(p2-p1σ2-c2σ2)q

整条供应链的收益函数:l=(p2-c1σ1σ1-c2σ2-c3σ1σ2)q

maxp2(l),maxp2(l2)，可由一阶导可得利润最大化:

l和l2同时达到最大时,得到:

p1=c1σ1+c3σ1

此时l1=0，l2和l达到最大，得到最大利润:

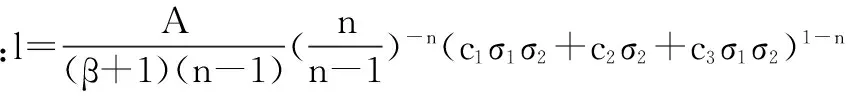
当A、β、n都为常数时，仅考虑整条供应链的利润影响为成本因子和损耗因子；当损耗α与η增大的同时l是减小的，不同种类农产品在供应链上的利润比例要随着A、β和n的不同而变化。

3.1.2均衡支付条件下农户与超市各占利润的比率。在整条供应链条件下定义al为超市的利润,(1-a)l为农户的利润,故可得:(1-a)l>l1①；al>l2②。由①得:

由②可得:

得到α的范围:

3.1.3均衡支付条件下损耗函数值的变化对α的影响。当n=2时，分析损耗对利润的影响和对均衡支付条件下农户和超市的所占利润比例的大小。

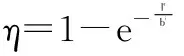
以土豆为例：b的取值为48，γ=1,ε=1.1,i=1.8；c1=0.6,c2=0.3,c3=0.3,p1=2元/kg。计算得出表1数据。

表1 土豆的二级供应链上需求双方所占的利润比例随流通时间增加而变化的数据

t天数∥dσα1-α2411.0310.534～0.7580.466～0.2414821.0690.549～0.7680.451～0.2327221.1100.565～0.7790.435～0.2219631.1540.582～0.7890.148～0.21112041.2000.600～0.8000.400～0.20014451.2500.620～0.8110.380～0.18916871.3020.640～0.8230.360～0.17719281.3580.662～0.8350.338～0.16521691.4160.685～0.8470.315～0.152

再以蕃茄为例：p1=3.9元/kg,c1=1元，c2=0.3元，c3=0.4元。b=48，γ=3,ε=1.4,i′=1.3，计算得出表2数据。

表2 蕃茄的二级供应链上需求双方所占的利润比例随流通时间增加而变化的数据

t天数∥dσα1-α2411.1430.50～0.740.5～0.26361.51.2660.55～0.760.455～0.2414821.4230.6～0.790.4～0.21602.51.6200.68～0.820.32～0.187231.8640.77～0.860.23～0.14843.52.1660.88～0.910.12～0.09

在上述例子中可以看出，番茄只能在6～7 d左右的时间里存在均衡支付的相对较为平衡的利润构成比例，而且番茄的利润比例增长幅度在单位时间里明显高于土豆，因此在较短的时间里面销售番茄会使农户获得较大的利润；而土豆在这一方面表现得较为缓和。随着时间的进一步延长可以看出，农户在番茄的整条供应链利润的比例存在较大跳跃，而土豆的整条供应链则表现得相对缓和。这主要是由于农产品本身的性质决定的，但通过改变流通时间就能控制供求双方的利润比例。

4 结论与讨论

该研究考虑了在博弈模型上供需双方在二级供应链上的利润比例随着流通时间增加而变化，在博弈模型的支付函数中引入随时间变化的损耗函数，运用合作博弈模型研究双方在整条供应链上的利润比例，在实例中分析了土豆和番茄这2具有代表性的农产品，进而计算得出相关数据。在确定各支付函数和损耗函数的参数的情况下得到如下结论：

(1)农超对接的二级供应链上供给方所占的利润比例小于需求方，这是由于二者的社会属性所决定的。

(2)不同种类的农产品在进行农超对接时应该按照农产品损耗的不同特点制定不同的支持政策，保证供给方在整条供应链上的利润。

(3)在建立农超对接的供应链时，应找出限制流通速度的瓶颈，让农产品以最快的速度流通，这样可以有效地保障整条供应链的利润和供给方较高的利润比例。

该研究进一步说明了农产品流通过程中时间的长短对农户在整条供应链上的利润比例的重要性以及不同农产品的损耗程度对均衡支付中供给方的利润比例的影响；并进一步说明了在农产品流通过程中供给双方合作的重要性以及损耗给二者的利润带来的影响，为农超对接模式广泛的推广和保证农户的利益提供一定的理论支持。

该研究基于社会实践调研所得的数据进行算例的计算，结论具有较高的可信度。此外，在以后的研究中，将会继续关注农超对接的合作博弈的相关问题，将研究方法与思路推广到三级供应链模型，更加仔细地考虑不同农产品的损耗对其本身的供应链上供给双方的利润比例的影响。该研究在构建供应链利润函数上面使用的经济学中较为经典的函数模型，没有找出限制这一现象的瓶颈，在未来的研究中会引进更加精确的模型和方法。

[1] 雷露.考虑从属失效的生鲜农产品物流损耗测量模型研究[J].山西财经大学学报，2012(S1)：91-93.

[2] PAULE M,PHAN THI GIAC TAM,DAO THE ANH.The role of organizations in supplying supermarkets with quality food in Vietnam[J].Food Policy,2010，35:71-77.

[3] PRITCHARD B,GODWIN M.The impacts of supermarket procurement on farming communities in India:evidence from rural Karnataka [J].Development Policy Review,2010,4(28)：438-450.

[4] LAU L H A,LAU S H,WANG C J.Pricing and volume discounting for a dominant retailer with uncertain manufacturing cost information[J].European Journal of Operation Research,2007,183：852-860.

[5] CHRISTIN SCHIPMANN,MATIN QAIM.Supply chain differetiation,contract agriculture,and farmers'marketing preferences:The case of sweet pepper in Thailand[J].Food Policy,2011，36：670-675.

[6] 席其鲁.基于博弈方法的农超对接中农户和超市的决策分析[J].新疆农垦经济，2012(8)：7-9.

[7] 刘欢欢.蔬菜直接配送_农超对接模式的双方合作利益博弈分析[J].江苏农业科学，2012，40(3)：389-391.

[8] 刘磊.农超对接模式中的合作博弈问题研究[J].管理工程学报，2014(4)：100-101.

[9] 殷丽玲.基于合作博弈的农超对接利益分配问题研究[D].北京：北京交通大学，2011：26-29.

[10] 任向阳.基于博弈模型的农产品供应链收益分配研究[J].物流技术，2013，32(9)：357-359.

[11] 崔丽.基于供应链质量控制的_农超对接_零供关系演化博弈分析[J].北京工商大学学报，2013(9)：48-50.

[12] 王丽娟.易腐农产品供应链中博弈分析[D].武汉：华中科技大学，2008.

[13] 张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2004.

[14] 金赛美.现代农产品市场体系构建研究[D].武汉：华中农业大学，2006.

Effects of Perishable Goods Circulation Time Increase on the Game between Supply and Demand

HE Peng-fei, GUO Biao*, PAN Qian-lan

(Department of Management Engineering, College of Engineering, Nanjing Agricultural University, Nanjing, Jiangsu 210031)

Considering the profit ratio distribution unreasonable condition of perishable goods circulation in the secondary supply chain, through the establishment of the perishable goods circulation profit game function, the profit function was analyzed to draw the biggest profit by the parties equilibrium conditions. Also considering dependent failure of the perishable goods, the perishable goods loss function about time was constructed; Combining loss function and profit game function, profit ratio changes with the circulation time of the parties on the supply chain were analyzed. It was found that circulation time increase the demand of the profit ratio gradually close to 1. When close to the perishable goods circulation time decay cycle, suppliers, the proportion of profits close to 0.

The perishable goods; Game; Circulation time; Loss function; Profit share

南京农业大学暑期社会实践活动项目。

何朋飞(1994-)，男，安徽蚌埠人，本科生，专业：物流工程。*通讯作者，在读博士，从事控制理论与控制工程研究。

2014-12-17

S-9;F 232

A

0517-6611(2015)04-330-03