Sigma-Delta调制器的设计与仿真

黄锐敏, 杨清河, 陈兴, 梅丹丹

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021；

2. 泉州市迈韦通信技术有限公司， 福建 泉州 362005)

Sigma-Delta调制器的设计与仿真

黄锐敏1, 杨清河2, 陈兴2, 梅丹丹1

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021；

2. 泉州市迈韦通信技术有限公司， 福建 泉州 362005)

摘要：提出一种基于线性系统分析和仿真拟合的5阶数字Sigma-Delta调制器的设计方法.Simulink仿真结果表明：与过采样率为64的4阶调制器比较，所设计的5阶Sigma-Delta调制器在过采样率降低到只有32的情况下，输出信噪比可以达到104 dB，比前者改善了6 dB.因此，在相同过采样率下，该5阶调制器可以得到更宽的信号带宽.

关键词：Sigma-Delta调制器； 过采样率； 数模转换； 积分非线性

Sigma-Delta调制技术提供了在超大规模集成电路(VLSI)上实现极高精度模数和数模转换的手段. 利用过采样和噪声整形算法，解决在传统模数、数模直接转换方式中遇到的转换精度要求与器件失配误差之间的矛盾，以及抑制差分和积分非线性引起的误差[1].因而在相同工艺误差条件下，能更有效地提高转换器的精度，即提供更高位数的转换器.同时，由于具有抗噪声的优点[2-6]，调制技术越来越多地应用在现代的集成整个系统的VLSI芯片中.本文将介绍一种基于线性系统分析和仿真拟合的5阶数字Sigma-Delta调制器的设计方法.

1Sigma-Delta调制器的线性系统模型

Sigma-Delta调制器和其他转换器一样，通过在时间上采样和幅度上量化来实现模数和数模转换.由于幅度上的量化，系统对信号的处理不再具有线性，所以整个Sigma-Delta调制器属于非线性系统.但是，如果输入信号为随机信号，量化的级数足够多，Sigma-Delta调制器的过采样率远远大于2，或者Sigma-Delta调制器整形滤波器系统传输函数H(z)的阶数足够高(大于2)，则量化器带来的量化误差将平均分布在量化区间上，从而可以近似为平均分布的量化噪声[7].

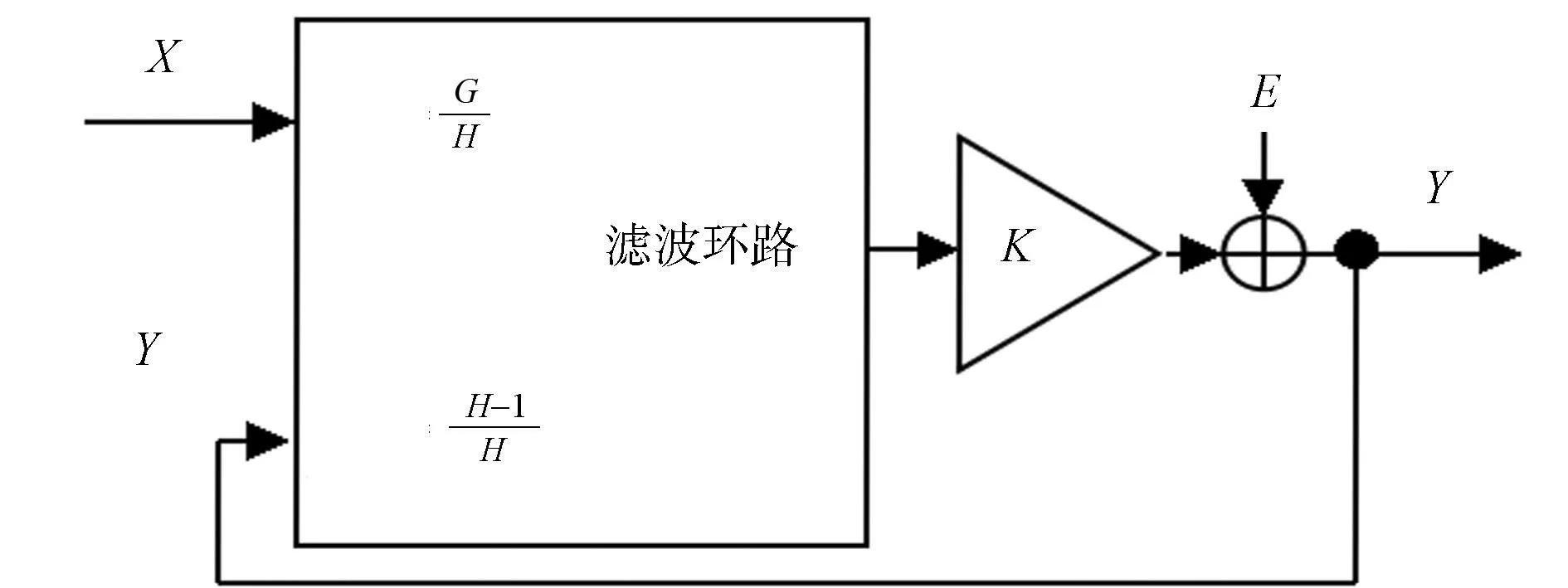
图1　Sigma-Delta调制器的线性系统模型Fig.1　Linear system model of Sigma-Delta modulator

基于这一假设，可以将Sigma-Delta调制器等效为线性系统模型，如图1所示.图1中：X为输入信号；Y为输出信号.根据梅森公式，可以得到输出信号，输入信号和量化器引起的噪声的关系式，即

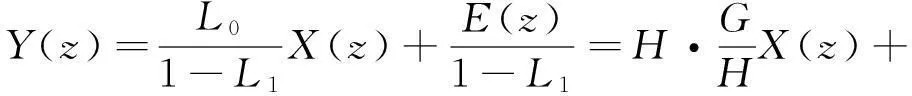
上式中：G为信号系统传输函数；H为噪声系统传输函数；L0为输入信号环路的系统传输函数；L1为噪声整形环路的系统传输函数.

2Sigma-Delta调制器的系统传输函数

根据Sigma-Delta调制器的线性系统模型，可以设计不同的系统环路结构L1，从而实现噪声系统传输函数H(z).级联积分器单环反馈具有结构简单，运算速度快的特点，经常被用在数字Sigma-Delta调制器的设计中，如图2所示.对于高于1阶的单环反馈调制器是有条件稳定的系统，所以H(z)的最大增益Hinf一般不能太大，否则系统无法正常工作.Hinf具体的数值由系统函数的阶数和量化器的量阶决定[8].基于线性系统模型的设计是一种近似方法，所以得到的系统函数最后需要仿真验证.

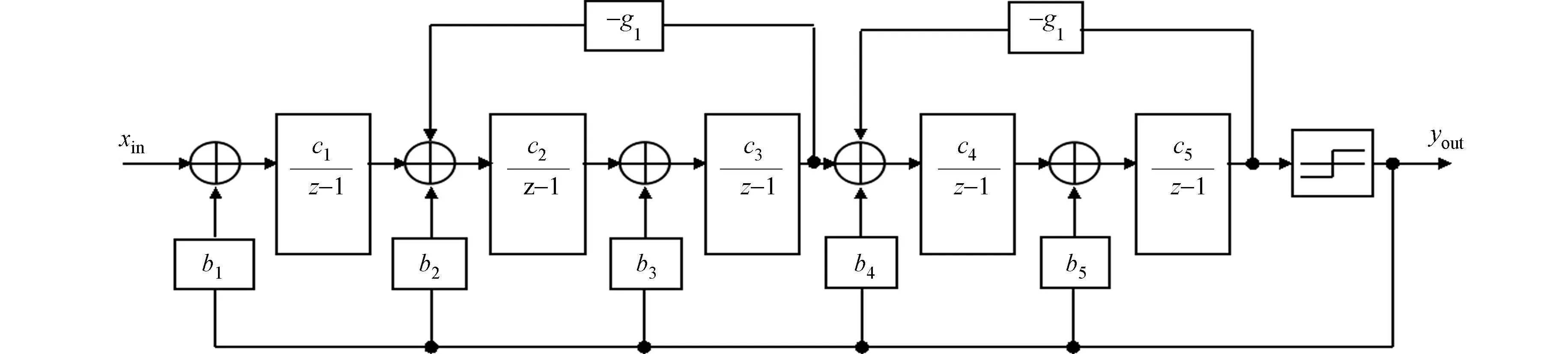
图2　级联积分器单环反馈结构的Sigma-Delta调制器Fig.2　Cascaded integrator single-loop feedback structure Sigma-Delta modulator

H(z)表示为H(z)=N(z)/D(z)，其中：有理函数N(z)，D(z)的根为H(z)的零点和极点[9].D(z)是取决于Hinf大小的ⅡR滤波器的传输函数，而N(z)由零点的分布决定[8].如果让H(z)的零点均匀地分布在基带内，而不是都处在z=1处，即N(z)≠(z-1)L，则同样增益的H(z)可以获得更高的信噪比.由Matlab的线性系统和Sigma-Delta调制器设计工具，可以综合得到一个5阶的噪声系统传输函数H(z)，即

(1)

另外，由图2的系统结构，设c1~5=1，其噪声环路的系统传输函数L1表达为

(2)

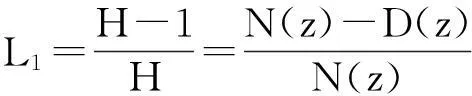
(4)

为了简化数字电路，实际的零点采用了两个近似：第一，N(z)单位圆上的零点采用L1中单位圆外的零点近似逼近；第二，为了简化反馈回路的乘法运算，反馈系数g1~2用2的负幂次2-M(M为正整数)来近似，反馈信号的二进制数值只要向左移M位，并舍去低M位数字就可以实现相应的系数相乘.

虽然以上近似得到零点不是最优的位置，但是能大大简化数字系统的实现，而信噪比的略微下降可以通过提高Hinf得到补偿.实际设计中，通过仿真得到的信噪比选择合适的M，可得到g1~2.由式(1)，(3)可得，g1≈2-1.997 2=0.002 8=2-8.48≈2-8；g2≈2-1.992 1=0.007 9=2-6.98≈2-7.

通过对式(4)左右两端关于z各阶幂次对应系数的匹配，可以得到一组关于b1~5的方程，解方程可以得到以b5为归一化因子的b1~5的比例系数.一般可以根据最后一级积分器精度要求的位数确定b5的数值，如b5=28.

利用各级积分器的量化噪声滤波特性，可以使后级的位数逐级递减，而图2中c1~5就是各级用来控制递减程度的增益系数.1/ROS≥c1~5.b5和c1~5确定后，b2~5的数值即可确定，g1~2的数值需要考虑c1~5而作相应的修正，使最后的环路增益保持不变.所有系数求出后，每级数字积分器的位数，可以通过Matlab的系统模型输入正弦信号仿真得到的最大动态范围来确定.

3多位5阶数字Sigma-Delta调制器的设计

对于采样率为32的5阶数字Sigma-Delta调制器的设计，由式(1),(3)，以及上述提到的近似规则可得g1=2-8，g2=2-7.由式(4)可以得到计算b1~5的方程，求逆后为

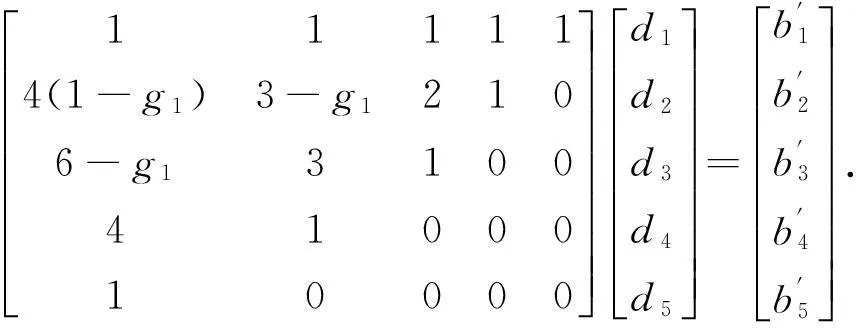
(5)

4仿真结果与比较

将c1~5和b1~5代入图2所示的数字Sigma-Delta调制器中，即可得到仿真拟合的Matlab模型.表1列出了不同H(z)最大增益Hinf和输入幅度为A的正弦波Asin(0.5n/ROS)仿真得到的信噪比RSN.仿真结果如图3所示.图3(a)显示的是数字Sigma-Delta调制器的输入和输出波形，图3(b)显示的是输出信号的幅度频谱.由图3(a)可知:调制器的输出，同时也是反馈信号在{±1,±3}之间跳变，具体取值可以通过对末级积分器的高2位二进制数判断得到，即采用的是2位的量化器.

表1　不同Hinf和输入幅度A仿真结果

(a) 输入输出波形 (b) 输出信号的幅度谱图3　5阶数字Sigma-Delta调制器仿真结果Fig.3　Simulation results of the fifth-order digital Sigma-Delta modulator

5结束语

基于线性系统分析和Matlab仿真拟合的5阶数字Sigma-Delta调制器，能够有效地设计稳定的Sigma-Delta调制器.对于3阶和4阶的Sigma-Delta调制器[10]，当过采样率等于32时，其信噪比分别为68.0,73.3dB；当过采样率等于64时，其信噪比分别为84.2,98.6dB.文中设计的5阶数字Sigma-Delta调制器，在过采样率降低一半的情况下，即等于32时，可以获得104.1dB的信噪比，比3阶和4阶调制器有大于5dB的改善.因此，需要宽带信号Sigma-Delta调制器的应用场合,可以考虑使用5阶调制器降低过采样率的要求.

参考文献：

[1]傅文渊，凌朝东.应用于电流型数模转换器的积分非线性误差优化方法[J].华侨大学学报：自然科学版，2012，33(44)：163-167.

[2]杨骁,杨静,凌朝东,等.ADSL中宽带ΣΔ调制器的系统设计[J].信号处理，2011,27(2):309-312.

[3]NORSWORTHY S R,SCHREIER R,TEMES G C.Delta-sigma data converters: Theory, design, and simulation[M].New York：Wiley-IEEE Press,1996:165-192.

[4]FRAPPE A,FLAMENT A,STEFANELLI B,et al.An all-digital RF signal generator using high-speed modulators [J].IEEE Journal of Solid-State Circuits Oct,2009,44(10):2722-2732.

[5]HUNG T,RODE J,LARSON L,et al.H-bridge class-d power amplifiers for digital pulse modulation transmitters[C]∥Digest of IEEE MTT-S International Microwave Symposium.Hawaii：IEEE Microwave Theory and Techniques Society，2007:1091-1094.

[6]LUSCHAS S,SCHREIER R,LEE H S.Radio frequency digital-to-analog converter[J].IEEE Journal of Solid-State Circuits,2004,39(9):1462-1467.

[7]GRAY R M.Quantization noise spectra[J].IEEE Transactions on Information Theory,1990,36(6):1220-1244.

[8]SCHREIER R.An empirical study of high-order single-bit delta-sigma modulators[J].IEEE Tran Circuits and Systems II,1993,40(8):461-466.

[9]SCHREIER R,TEMES G C.Understanding delta-sigma data converters[M].New York：John Wiley and Sons Inc，2004:219-253.

[10]HUANG R,LOTZE N,MANOLI Y,On design a high speed sigma delta DAC modulator for a digital communication transceiver on chip[C]∥Proceeding of 11th EUROMICRO Conference on Digital System Design Architectures, Methods and Tools.Parma:IEEE Computer Society,2008:53-60.

(责任编辑： 陈志贤英文审校： 吴逢铁)

Design and Simulation of a Sigma-Delta Modulator

HUANG Rui-min1, YANG Qing-he2, CHEN Xing2, MEI Dan-dan1

(1. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China;

2. Quanzhou Maiwei Communication Technology Company Limited， Quanzhou 362005, China)

Abstract：This paper introduce a design method for the fifth-order digital Sigma-Delta modulator based on linear systems analysis and simulation fitting. Simulink simulation result shows that compared to the fourth-order modulator of oversampling ratio of 64, the oversampling ratio of the designed fifth-order modulator reduces to only 32, output signal to noise ratio can reach 104 dB, which improves 6 dB over the former design. Therefore, in the same oversampling ratio, this fifth-order modulator can get wider signal bandwidth.

Keywords：Sigma-Delta modulator; oversampling ratio; digital to analog conversion; integral nonlinearity

基金项目：中央高校基本科研业务费专项基金资助项目，华侨大学科研基金资助项目(12Y0308)； 福建省泉州市科技计划资助项目(2012Z98)

通信作者：黄锐敏(1971-)，男，讲师，博士，主要从事数字信号处理电路的研究.E-mail:huangruimin@hqu.edu.cn.

收稿日期：2013-09-04

中图分类号：TN 79

文献标志码：A

doi:10.11830/ISSN.1000-5013.2015.01.0007

文章编号：1000-5013(2015)01-0007-04