一类奇异Markov链的遍历性



一类奇异Markov链的遍历性

李冬霞，李星星，逯玲娜

(郑州城市职业学院 基础部,河南 郑州452370)

摘要：考察了一类奇异Markov链的遍历性。首先给出了此马氏链的Ray-Knight紧化，然后利用遍历定理等讨论了这类马氏链的遍历性，并给出了相应的证明。

关键词：Ray-Knight紧化;Markov链;遍历性

近二三十年，有大量的文献讨论了连续时间马氏链的遍历性,但这些文献均假设Q矩阵是正则的，马氏链是非爆炸的，如Anderson(1991)[1]、Chen(1992)[2]、Meyn等[3]。另外，Lund等[4-5]还讨论了随机单调情形下的遍历性，但是用上述方法均无法讨论下面所给出的一类奇异马氏链的遍历性。

首先给出此马氏链的Ray-Knight紧化：

设E={1,2,…}，

(1)

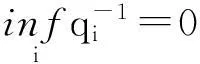
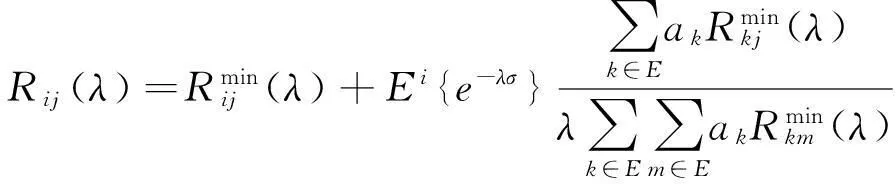
(2)

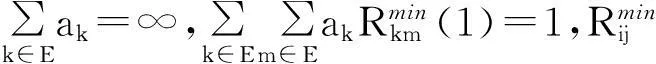
1预备知识

定义1[8]设pij(t)是E={0,1,…}上诚实且标准的转移函数，pij(t)的密度矩阵为Q=(qij),qi=-qii,则X=(Ω,f,ft,Xt,θt,Px)是pij(t)所对应的正规链。

定义2[8]pij(t)称为遍历的(正常返的)，如果存在概率测度πi,i∈E，使得：

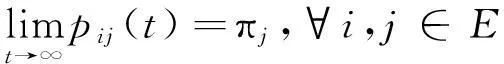
πi,i∈E称为pij(t)的平稳分布。

2主要结论及证明

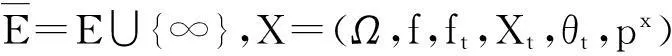
证明：由

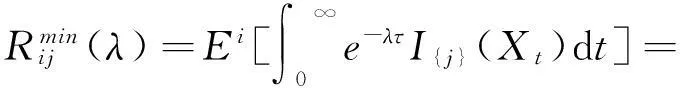
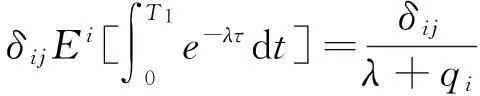
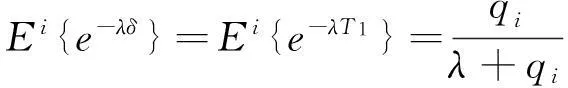
得到：

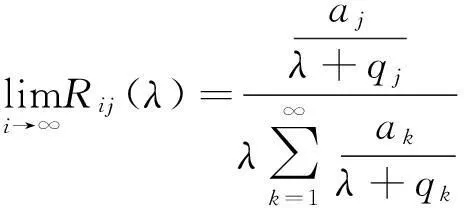
X=(Ω,f,ft,Xt,θt,px)为P(t)对应的正规链(见文献[7])。

证毕。

定理3pij(t)是遍历的，并且pij(t)的平稳分布为:

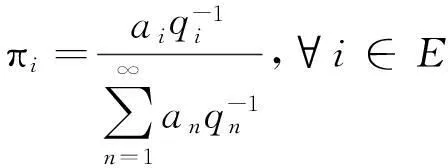
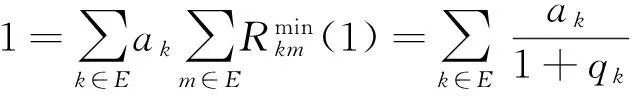
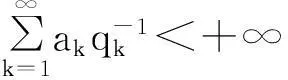
(2)诚实的转移函数pij(t)的预解式为：

故由遍历定理知：

由(1)(2)知pij(t)是遍历的，并且pij(t)的平稳分布为：

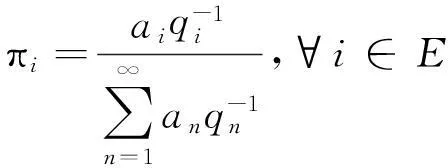
证毕。

参考文献：

[1]AWJ.Continuous-TimeMarkovChains[M].NewYork:Springer,1991:61-67.

[2]ChenMF.FromMarkovChainstoNon-EquilibriumParticleSystems[M].HongKong:WorldScientificPublishingCompany,1992:139-150.

[3] Meyn S P, Tweedie R L. Computable bounds for geometric convergence rates of markov chains[J].Ann.Appl.Prob,1994,4(4):981-1 011.

[4] Lund R B, Meyn S P, Tweedie R L. Computable exponential convergence rates for stochastically ordered markov processes[J]. Ann.Appl.Prob,1996,20(1):218-237.

[5] Lund R B, Tweedie R L. Geometric convergence rates for stochastically ordered markov chains[J].Math.Oper.Res,1996,16(1):182-194.

[6] 侯振挺.Q过程的唯一性准则[M].长沙:湖南科学技术出版社，1982.

[7] Williams D. Diffusions Markov processes and martingales[M].Cambridge:Cambridge University Press,1979:158-170.

[8] 王梓坤.生灭过程与马尔科夫链[M].北京:科学出版社，2005.

(责任编辑：张英健)

Ergodicity of a Class of Singular Markov Chain

LI Dongxia, LI Xingxing, LU Lingna

(Department of Mathematics， City University of Zhengzhou, Zhengzhou Henan452370, China)

Abstract：This paper investigates the ergodicity of a class of singular Markov Chain Firstly, Ray-Knight compactness of the Markov chain is given. Then,by using the ergodic theorem we discuss the ergodicity of this kind of Markov chain and give the corresponding proof.

Keywords：Ray-Knight compactification; Markov chain; ergodicity

作者简介：李冬霞(1979-)，女，河南新密人，硕士，主要研究方向为概率与数理统计。

收稿日期：2014-10-14

中图分类号：O221

文献标识码：A

文章编号：1671-5322(2015)01-0020-02

doi:10.16018/j.cnki.cn32-1650/n.201501005