武器系统预防性维修间隔期的多目标决策研究

都业宏，郁浩，赵静，张扬，杨春来

(1. 中国白城兵器试验中心，吉林 白城137001;2. 北京理工大学 机电学院，北京100081)

0 引言

某型武器系统是典型的轻型复杂武器装备，包括火力系统、计算机系统、光电系统、通信系统等多个模块。相比于大型装备，它的集成度更高，在战斗使用过程中面临着多种故障和失效模式。这一特点使得它的维修保障成为该武器系统高可靠性和高安全性的保证。对于目前维修保障一个复杂装备系统所需的费用，文献［1 -2］认为其通常要占到装备全寿命周期费用的60%以上，部分装备高达70% ～80%，极大地影响着全系统的总体运行费用。因此，进行武器系统维修方式的研究，制定合理的武器系统维修制度，对于有效预防故障发生，提高维修保障效率，进而提高装备系统的使用可用度和防止过度维修具有重要的意义。

通常武器系统的维修分为预防性维修和修复性维修［3］。由于预防性维修可以尽量安排在非战斗时间或非战备值班时间内进行，能使装备系统停机造成的损失减到最小，所以到目前为止，在机械系统中还是广泛采用这种维修方式［4-6］。美国国防部分别于20 世纪60年代和90年代提出了以可靠性为中心的维修RCM 和RCM-Ⅱ. 至今，RCM-Ⅱ广泛应用于军事和民用领域。RCM 综合考虑武器系统的可靠性、维修保障的可行性和费用，按照以最少的维修资源消耗保持武器系统固有可靠性的原则，应用逻辑决断的方法确定武器装备预防性维修要求［7］。

目前，预防性维修系统多以平均故障间隔时间(MTBF)为输入，输出为预防性维修间隔时间［6，8-12］。最佳预防性维修间隔多以故障率模型为基础，通过威布尔分布拟合参数，进而进行最佳预防性维修间隔的确定。如申桂香等在文献［6］中，利用这种思路很好地解决了数控机床最佳预防性维修间隔时间的确定问题。文献［12 -13］利用这种思路解决了相应武器系统的预防性维修问题。但如果武器系统均照搬此法，将得到与现实不相符合的结果。与连续运转的工业机器的MTBF 不同，武器系统的MTBF 受人为因素影响很大，如库存期间长时间不使用等，而且，目前武器系统的MTBF 实时获取是非常困难的。但武器系统的故障与射弹量密切相关，而且武器系统发生故障时的间隔射弹量数据易于统计，以间隔射弹量确定预防性维修的时机在实际中更易于操作。但是，用射弹量表征武器装备的故障率，将面临着使用可用度和维修费用难以解析表达的问题。因此，本文在利用现场采集故障数据的基础上，建立一种在维修状态下最佳预防性维修间隔射弹量的数学模型，针对使用可用度和维修费用这两个重要目标的实际含义，用该模型对这两个重要目标进行了解析表达。为确定武器系统的最佳预防性维修间隔射弹量，本文采用较为成熟的多目标粒子群算法针对使用可用度和维修费用这两个目标进行了优化决策，得到了符合要求的满意解。

1 故障率模型

故障率模型有多种，如威布尔分布、指数分布和对数正态分布等。不论故障率模型呈现何种分布形式，均需进行分布模型拟合、线性相关性检验等计算，以获得准确的故障率模型。本文中主要应用到了二参数威布尔分布模型。

1.1 二参数威布尔故障率函数拟合

对于复杂系统，威布尔分布物理意义明确，并为实践证明其具有广泛的适应性，以它为基础所形成的复杂可靠性模型已受到较为广泛的应用［6］。

假设武器系统的故障间隔射弹量服从二参数威布尔分布，其概率密度函数、分布函数和故障率函数分别为

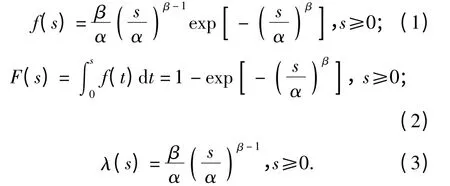
式中:s 为故障间隔射弹量;采用MATLAB(2014b 版本)中的wblfit 函数，根据已知故障数据进行二参数威布尔分布参数估计可得到相应的β 和α 值。假设β=β0，α=α0，则故障率函数可表示为

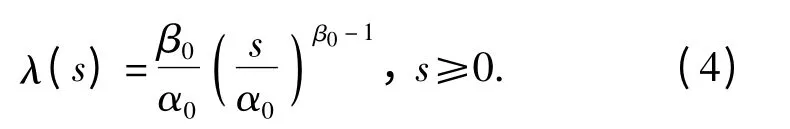
1.2 威布尔分布的线性相关性检验

采用相关系数法对威布尔分布的拟合效果进行检验。相关系数为

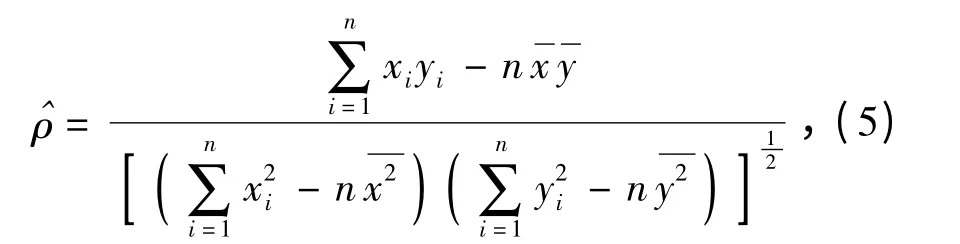
式中:x = s;y = λ(s);n 为故障数据个数。当＞ρ(n-2，α')时，认为x 与y 之间的线性相关性显著。其中，ρ(n-2，α')为相关系数的临界值，可查表求出，亦可用近似公式计算。选取显著性水平α' =0.1，采用近似公式计算［13］，则

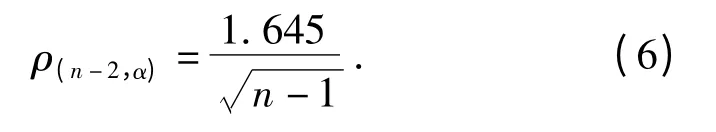
2 决策单目标表示

2.1 使用可用度

武器系统的预防性维修流程如图1所示。假设预防性维修间隔射弹量为N0，在系统射击N0发弹后进行预防性维修，平均预防性维修时间为(单位h)，维修后武器系统继续工作，但未到工作射弹量N0，而是在射弹量为N1时刻发生故障，立即对武器系统进行修复性维修，平均修复性维修时间为，修复后工作到N2，则当N1+N2=N0后再次进行预防性维修。

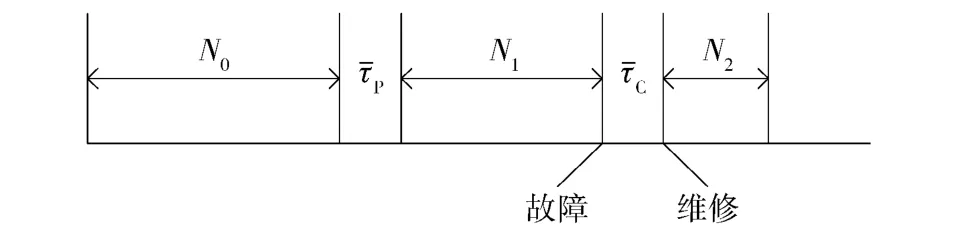
图1 武器系统的预防性维修流程Fig.1 Preventive maintenance process of a weapon system

从图1可以看出，N0就是平均工作射弹量MUA.由于本文以射弹量为单位表征武器系统的故障率，与以往用时间为单位表征使用可用度有较大差别，因此本文根据使用可用度的实际物理含义，给出了用射弹量表征的用于描述武器系统的使用可用度的定义。

定义:使用可用度是指武器系统在期望工作射弹量内的平均工作效率。具体用(7)式进行计算:

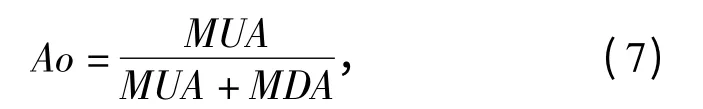
式中:MDA 为平均不可工作射弹量。MDA 与武器系统的实际作战需求相对应的，对于具体的某种武器系统来说，MDA 满足以下关系:

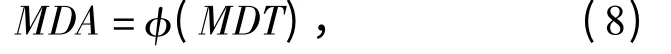
式中:MDT 为平均故障时间;φ()为MDA 与MDT 之间的转换关系，对于具体的武器系统而言，φ()为MDA 与MDT 之间的正比例关系。又

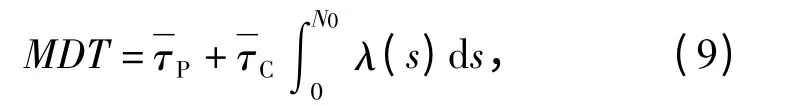
武器系统的使用可用度Ao 为

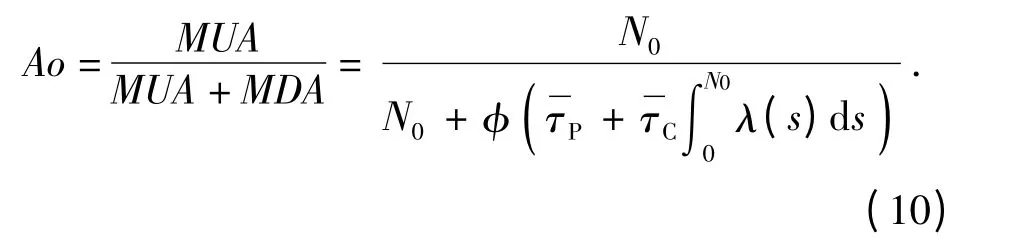
对(10)式求导并使d(Ao)/ds =0，可得武器系统在不考虑维修费用的条件下的最佳维修间隔射弹量满足

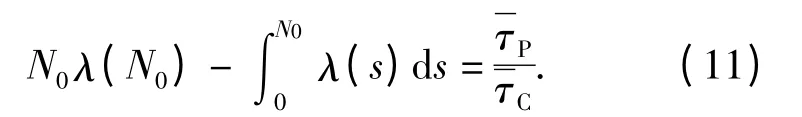
故障率函数λ(s)对于不同分布，有不同的形式，所以通过(10)式和(11)式得到的结果也不尽相同。

对于早期故障期，武器系统性能随着时间推进而改善，故障率函数λ(s)为减函数，则N0λ(N0)＜为负，N0无合理解。再此种情况下，预防性维修实际上有害无益，不可取。

对于偶然故障期，λ(s)为常数，即其故障率函数服从指数分布，此时=0，表明武器系统整个寿命期间，下一个时间增量的视效率保持不变，与它工作多长时间无关。说明在此情况下进行定期预防性维修时无效的。维修将不影响故障率。

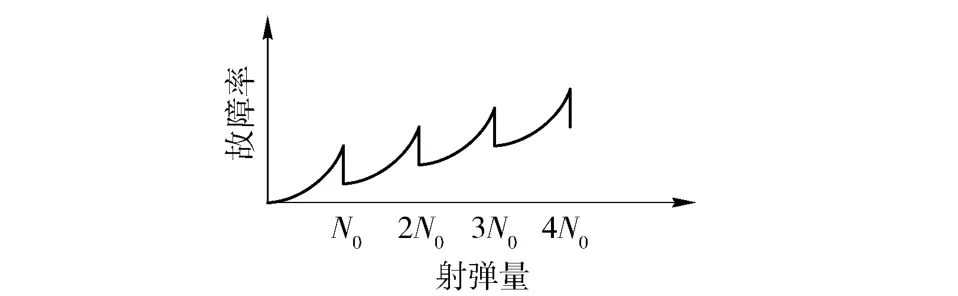
图2 预防性维修后故障率示意图Fig.2 Schematic diagram of failure rate after preventive maintenance

对处于耗损期的系统，由(10)式和(11)式可以得到合理的最佳维修间隔射弹量为

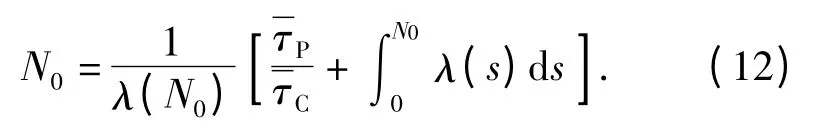
如果系统故障率函数符合二参数威布尔分布，即故障率如(3)式所示，则系统的最佳预防性维修间隔射弹量N0可表示为

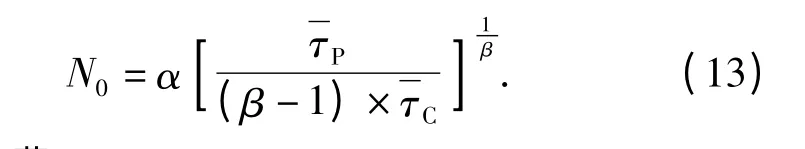
2.2 维修费用

为方便用符号的形式解析表达维修费用，现对有关参数进行符号设定。

寿命L，预期维修费用EMC，预防性维修费用PMC，修复性维修费用CMC，预防性维修单价PMUP，修复性维修单价CMUP，等间隔预防性维修第i 次预防性维修后故障率为λpi(s). 不同的维修等级条件下的预防性维修会使武器系统的故障率以不同的比例下降。针对本文研究的具体武器系统，设定故障率的降低比例为0.5，当i ×N0≤s≤(i +1)×N0时，

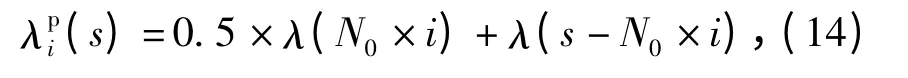
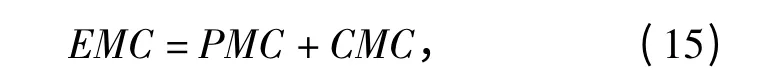
式中:PMC = floor (L/N0- 1)PMUP，CMC =为MATLAB 中取整运算函数。

3 多目标决策模型

某型武器系统鉴定试验中获得了大量的故障数据，部分数据见表1，其中s 表示故障间隔射弹量。该武器系统寿命L 为30 000 发，预防性维修单价PMUP 为600 元，修复性维修单价 CMUP 为1 500 元为2 h为0.2 h，φ(x)=120x 发/h.

应用1.1 节中的方法对表1中的数据进行故障率分布模型拟合，得到β =1.344 5，α =593.289 9，则故障率函数可表示为

表1 某型武器系统的故障数据Tab.1 Failure data of a weapon system

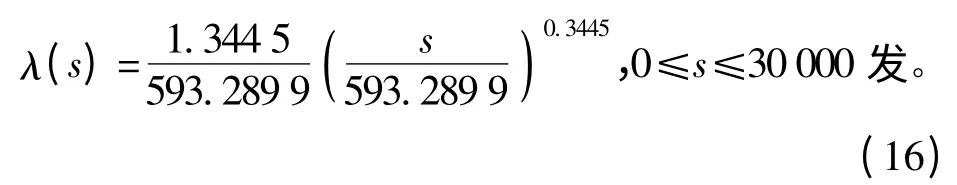
故障率函数如图3所示，从中可以看出，该武器系统的故障率是随射弹量逐渐增加的。

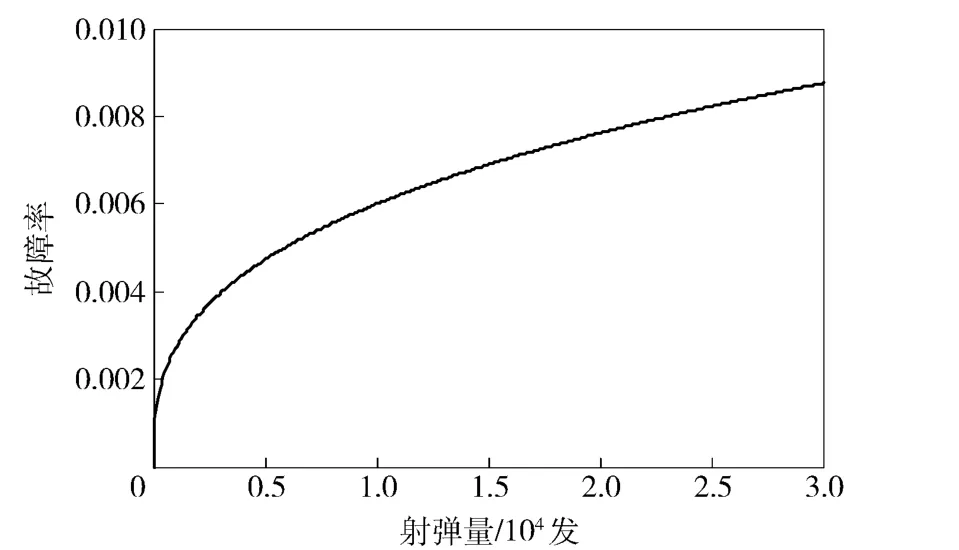
图3 故障率曲线Fig.3 Failure rate curve

应用1.2 节中的方法对得到的模型进行线性相关性检验。由(5)式计算得，=0.975 8. 选取显著性水平为0.1，由(6)式计算得，ρ(n-2，α')=0.343 0，因为＞ρ(n-2，α')，所以可认为该武器系统的故障间隔射弹量服从参数为β =1.344 5 和α =593.289 9 的二参数威布尔分布。

因此，该武器系统故障率函数为(16)式所示函数。将其带入(14)式中，则

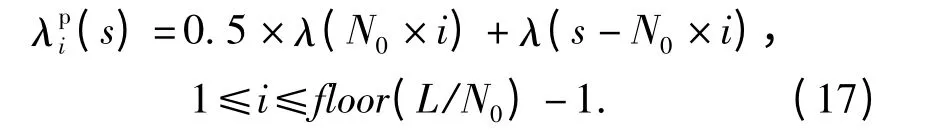
由(10)式和已知条件得

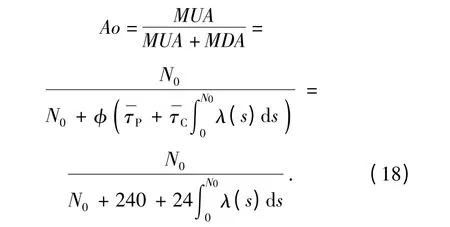
由(15)式、(17)式和已知条件得

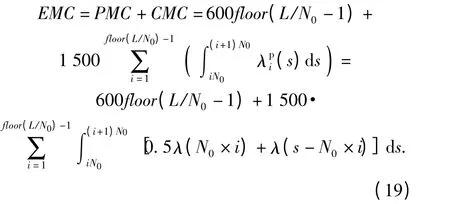
3.2 目标函数

对于武器系统而言，总希望其使用可用度最大，而维修费用最少。这两个目标在一定程度上存在着矛盾，希望能够找到可同时兼顾两个目标的方案。即，

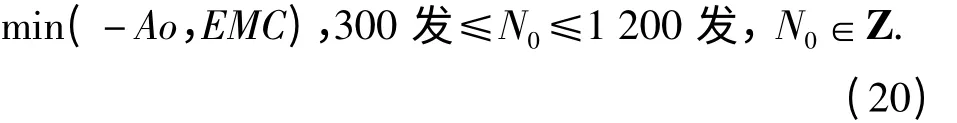
4 多目标粒子群算法

实际工程优化问题中，很多问题是多目标优化问题。相对于单目标优化问题，多目标优化问题的显著特点是优化各个目标使其同时达到综合的最优值。然而，由于多目标优化问题的各个目标之间往往是相互冲突的，比如本文的研究对象，在满足使用可用度最优的同时，维修费用可能会很高;或者维修费用最优时，使用可用度会很低。因此，一般适用于单目标问题［5］的方法难以用于多目标问题的求解。本文采用多目标粒子群算法对所研究问题进行决策，主要是基于3 点考虑:1)多目标粒子群算法的局部寻优能力较强，根据具体问题的求解范围，通过合理地设置算法参数，能够避免粒子群在局部点过早收敛;2)多目标粒子群算法应用较为成熟［14-19］，算法思想易于理解;3)算法实现相对容易。

多目标粒子群算法的流程如图4所示。其中，种群初始化模块随机初始化粒子的位置和速度，适应度值计算是指根据适应度值计算公式计算个体适应度值，粒子最优更新模块根据新的粒子位置更新个体最优例子。非劣解集更新模块根据新粒子支配关系筛选非劣解。粒子速度和位置更新模块根据个体最优例子位置和全局粒子位置更新粒子速度和位置。

图4 多目标粒子群算法的流程图Fig.4 Flow chart of multi-objective particle swarm optimization

4.1 适应度计算

令粒子适应值为min(-Ao(Ni0))和min(EMC(Ni0))，i 为粒子序号，则Pi= min(- Ao(Ni0))/(-Ao(Ni0))和Qi=min(EMC(Ni0))/EMC(Ni0)分别为第i 个粒子Ni0的使用可用度和维修费用适应度。

4.2 筛选非劣解集

筛选非劣解集主要分为初始筛选非劣解集和更新非劣解集。初始筛选非劣解集是指在粒子初始化后，当一个粒子不受其他粒子支配(即不存在其他粒子的min(-Ao(Ni0))和min(EMC(Ni0))均优于该粒子)时，把该粒子放入非劣解集中，并且在粒子更新前从非劣解集中随机选择一个粒子作为群体最优粒子。更新非劣解集是指当新粒子不受其他粒子以及当前非劣解集中粒子的支配时，把新粒子放入非劣解集中，并且每次粒子更新前都从非劣解集中随机选择一个粒子作为群体最优粒子。

4.3 粒子速度和位置更新

粒子更新公式如下:

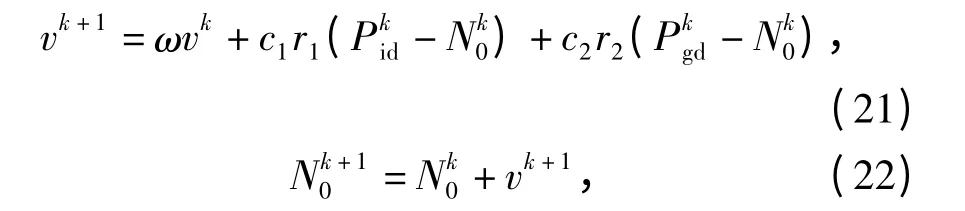
式中:ω 为惯性权重;r1和r2为分布于［0，1］区间的随机数;k 是当前迭代次数;Pkid为个体最优粒子位置;Pkgd为全局最优粒子位置;c1和c2为常数;v 为粒子速度;Nk0为第k 个粒子位置。

4.4 粒子最优化

粒子最优包括个体最优粒子和群体最优粒子，其中个体最优粒子的更新方式是从当前新粒子和个体最有粒子中选择支配粒子，当两个粒子都不是支配粒子时，从中随机选择一个粒子作为个体最优粒子。群体最优粒子为从非劣解集中随机选择的一个粒子。

5 优化结果与讨论

该问题是一个多目标单自变量问题，是一个预先设计过程，问题的主旨在于自变量在取值区间内寻找到该问题的满意解，不要求计算过程的高效性，而是尽量寻找到全局的满意解，避免早熟现象。这些条件易通过设置算法的相关参数得到满足。针对本问题，采用第4 节中的优化算法，选取种群规模为100，迭代4 975 步，对3.2 节的目标函数进行计算得到如下结果，如表2和图5所示。

图5中圆圈处的点的集合即为多目标粒子群算法针对第3 节中建立的多目标优化问题模型所求得的支配解集。从计算结果可以看出，使用可用度Ao和维修费用EMC 之间存在着一定矛盾，随着预防性维修间隔N0的增大，使用可用度Ao 逐渐增大，而EMC 也逐渐增大。实际进行维修决策时，具体的维修指标要求会缩小以上可行解集的范围，得到令决策者满意的若干满意解或无解。如在维修费用EMC 约束为不大于135 440 元，使用可用度Ao 约束为不小于0.76%的条件下，预防性维修间隔N0满足{N0|766 发≤N0≤794 发，N0∈Z}为满意解集。同样地，如在维修费用EMC 约束为不大于135 440 元，使用可用度Ao 约束为不小于0.77%的条件下，预防性维修间隔N0将无解，说明这是一个无法满足的预防性维修决策要求。

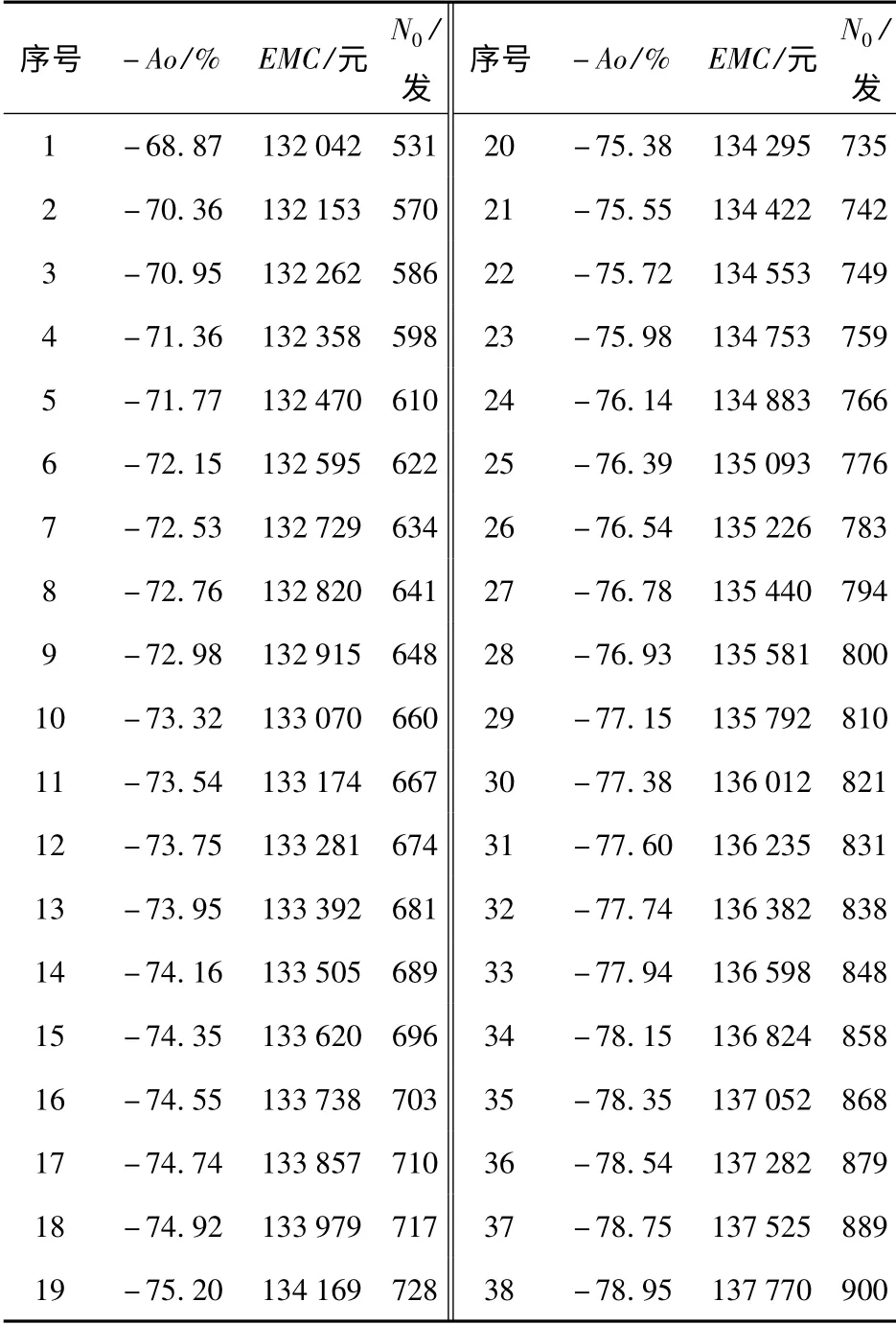
表2 支配解集Tab.2 Dominated solutions

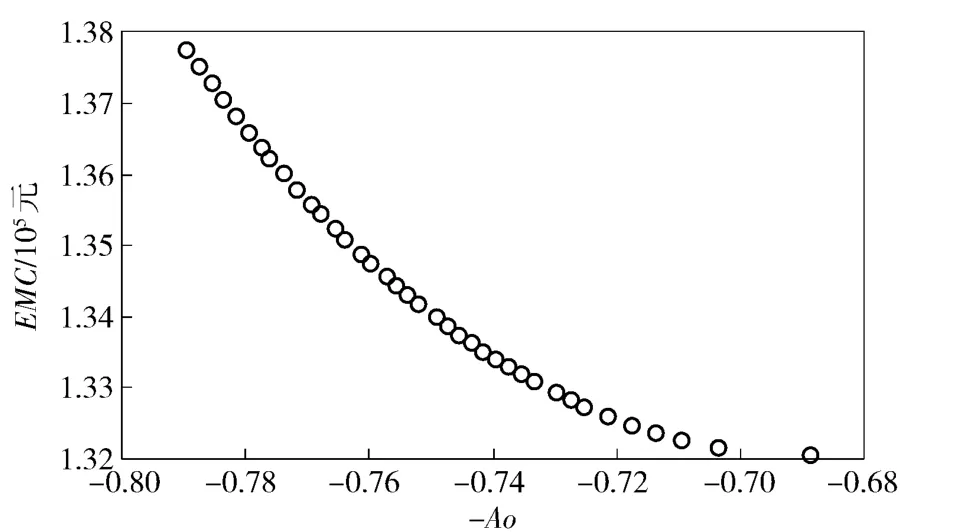
图5 支配解集示意图Fig.5 Schematic diagram of dominated solutions

此处获得的结果仅是通过应用表1中的故障数据估计到的武器系统故障率模型和本文所述方法进行优化计算的结果，旨在展示以射弹量为单位进行预防性维修决策的方法。即使进行了预防性维修，随着武器系统的使用，在到达寿命之前，仍可能发生故障。当发生新的故障时，应补充更新武器系统的故障数据，利用本文所述方法重新估计武器系统的故障率模型，并优化计算更新后的目标函数，动态地进行武器系统的预防性维修决策。

6 结论

本文在分析了典型的武器系统故障特点后，利用某型武器系统试验中的故障数据建立了用射弹量表征武器系统的故障率模型。针对使用可用度和维修费用这两个重要目标的实际含义，用该模型对这两个重要目标进行了解析表达。利用多目标粒子群算法，以使用可用度和维修费用为优化目标，针对某型武器系统进行了维修决策，得到了可行解集。通过全文的研究，得出如下结论:

1)进行预防性维修决策时需要根据武器故障的特点建立故障率模型，不合理的模型将得到不切实际的决策建议。

2)用射弹量表征武器系统的故障率，物理意义较为明确，且试验数据获取容易。

3)本文给出了用射弹量表征的使用可用度定义，该定义根据使用可用度的实际物理含义给出，为维修的多目标决策提供了方便。

4)用粒子群算法进行预防性维修间隔的多目标决策得到的是一个可行解集，合理的决策指标要求将会得到若干个满意解;不合理的决策指标要求将会无解。

5)预防性维修决策是一个动态的过程，应该随着武器系统故障数据的更新而动态地进行决策。

References)

［1］Kumar U D，Crocker J. 可靠性、维修性与后勤保障——寿命周期方法［M］. 刘庆华，宋宁哲，刘根，等，译. 北京:电子工业出版社，2010.Kumar U D，Crocker J. Reliability，maintenance and logistic support:a life cycle approach［M］. LIU Qing-hua，SONG Ning-zhe，LIU Gen，et al，translated. Beijing:Publishing House of Electronics Industry，2010. (in Chinese)

［2］于永利，郝建平，杜晓明，等. 维修性工程理论与方法［M］.北京:国防工业出版社，2007.YU Yong-li，HAO Jian-ping，DU Xiao-ming，et al. Maintainability engineering theory and methods［M］. Beijing:National Defense Industry Press，2007. (in Chinese)

［3］宋太亮，张宝珍，丁利平，等. GJB451A—2005 可靠性维修性保障性术语［S］. 北京:中国人民解放军总装备部，2005.SONG Tai-liang，ZHANG Bao-zhen，DING Li-ping，et al.GJB451A—2005 Reliability，maintainability and supportability terms［S］. Beijing:The PLA General Equipment Department，2005. (in Chinese)

［4］杜青玲，李美芳，刘家科. 机械设备预防维修周期的确定［J］.机床与液压，2000，28(6):92 -93.DU Qing-ling，LI Mei-fang，LIU Jia-ke. Decision on the period of preventive maintenance about mechanical equipment［J］. Machine Tool ＆ Hydraulics，2000，28(6):92 -93. (in Chinese)

［5］SUN Y，MA L，MATHEW J. Failure analysis of engineering systems with preventive maintenance and failure interactions ［J］.Computers ＆ Industrial Engineering，2009，57(2):539 -549.

［6］申桂香，谷东伟，张英芝，等.数控机床最佳预防维修间隔时间的确定［J］. 重庆大学学报，2012，35(1):7 -10.SHEN Gui-xiang，GU Dong-wei，ZHANG Ying-zhi，et al. Optimal preventive maintenanace interval period of CNC［J］. Journal of Chongqing University，2012，35(1):7 -10. (in Chinese)

［7］Moubray J. Reliability-centered maintenance II［M］.US:Industrial Press，1997.

［8］邵延君. 基于故障预测的武器装备系统预防性维修策略研究［D］. 太原，中北大学，2013:9 -48.SHAO Yan-jun. Weapon equipment preventive maintenance strategy reaearch［D］. Taiyuan:North University of China，2013:9 -48. (in Chinese)

［9］王灵芝. 以可靠性为中心的高速列车设备维修决策支持系统研究［D］. 北京，北京交通大学，2011:31 -60.WANG Ling-zhi. Research on reliability-centered maintenance decision and support system for high-speed train equipment［D］，Beijing:Beijing Jiaotong University，2011:31 -60. (in Chinese)

［10］张耀辉，郭金茂，单志伟，等. 装备预防性维修的维修级别逻辑决策分析方法［J］. 装甲兵工程学院学报，2008，22(5):40-44.ZHANG Yao-hui，GUO Jin-mao，SHAN Zhi-wei，et al. Maintenance level logic decision analysis method of preventive maintenance［J］. Journal of Academy of Armored Force Engineeing，2008，22(5):40 -44. (in Chinese)

［11］余勃彪，侯健. 基于威布尔模型的舰炮武器预防性维修系统构建与优化［J］. 机械，2012，39(5):29 -32.YU Bo-biao，HOU Jian. Study on the construction for the preventive maintenance system of naval gun weapon system［J］. Machinery，2012，39(5):29 -32. (in Chinese)

［12］李剑涛，蒋里强，黄立坡. 装备最佳预防性维修间隔时间研究［J］. 装备指挥技术学院学报，2004，15(3):26 -29.LI Jian-tao，JIANG Li-qiang，HUANG Li-bo. Study on the interval in the best equipment preventive maintenance［J］. Journal of the Academy of Equipment Command ＆ Technology. 2004，15(3):26 -29. (in Chinese)

［13］王超，王金. 机械可靠性工程［M］. 北京:冶金工业出版社，1992.WANG Chao，WANG Jin. Mechanical reliability engineering［M］.Beijing:Metallurgical Industry Press，1992.(in Chinese)

［14］Kennedy J，Eberhart R C. Particle swarm optimization［C］∥Proceedings of IEEE Inernational Conference on Neural Networks.Piscataway:IEEE Service Center，1995:1942 -1948.

［15］Fieldsend J E，Singh S. A multiobjective algorithm based upon particle swarm optimization:an efficient data structure and turbulence［C］∥UK Workshop on Computational Intelligence. Birmingham，UK:University of Birmingham，2002:37 -44.

［16］Mastaghin S，Teich J. Strategies for finding good local guides in multiobjective particle swarm optimization(MOPSO)［C］∥Proceedings of 2003 IEEE Swarm Intelligence Symposium. Indianapolis:IEEE，2003:26 -33.

［17］Li X. A non-dominated sorting particle swarm optimizer for multiobjective optimization［C］∥Proceedings of the Genetic and Evolutionary Computation Conference. Berlin:Springer，2003:37 -48.

［18］Fieldsend J E. Multi-objective particle swarm optimization methods［D］. Exeter，UK:Department of Computer Science，University of Exeter，2004.

［19］DU Ye-hong，CUI He，LI Bing，et al. Reasearch on regional coverage with LAVs on MOPSOA［J］. Journal of Information ＆Computional Science，2015，12(6):2081 -2092.