帕累托最优在车辆底部防护结构设计中的应用研究

魏然，王显会，周云波，王良模，郑雅丽

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

防护型车辆的主要威胁之一是来自地雷和简易爆炸装置(IED)的爆炸冲击［1］。底部结构受爆炸冲击波袭击后在极短时间产生大塑形变形，威胁驾驶室内乘员安全，因此，其防护设计需要从底部结构的抗爆炸冲击特性入手［2］。为此防护型车辆底部往往采用V 型、多层结构［3-4］等，以增加车辆的抗爆炸冲击能力。但这类结构会增加车辆整备质量、减小整车的离地间隙，降低车辆的机动性和通过能力，Grujicic 等［5］利用仿真与试验，研究了车辆抗爆炸冲击性能与机动性的矛盾关系。如何协调防护能力与整车性能间的关系是车辆底部防护结构设计的研究重点之一。同时，该结构的优化设计是一个强非线性、多参数的高维多目标全局优化问题［6-8］，其模型复杂、计算规模大(有限元单元数目超过百万)，一般方法很难在设计周期允许的时间内实现车身底部结构的优化。

本文以车辆底部结构中各钣金件的厚度、几何形状为设计变量，建立了以车辆底部防护结构的质量、比吸能和驾驶室地板变形挠度、冲击加速度为目标函数的优化模型，通过帕累托(Pareto)最优方法，对设计变量进行合理搭配，最终得到了该底部防护结构的优化设计方案，并探讨了不同的优化策略对各目标函数的影响。

1 车辆底部结构响应仿真

以某防护型车身为对象，建立了该车辆的1/2有限元模型，对零部件进行合理配重，其质心位置与满载时相同。车辆底部的爆炸空气流场模型覆盖整个底部结构(见图1(a))，地雷当量为8 kg(STANG 4569 的3 级防护标准［9］)。结合多物质单元(ALE)算法与流-固耦合(FSI)算法［10］对地雷爆炸环境下车辆底部结构响应进行了仿真分析。仿真中未考虑地雷爆炸环境下的热效应、车身中焊点与铰链的失效。仿真模型(包括空气流场、地雷替代物)单元总数为1 112 746，节点总数为1 148 829.

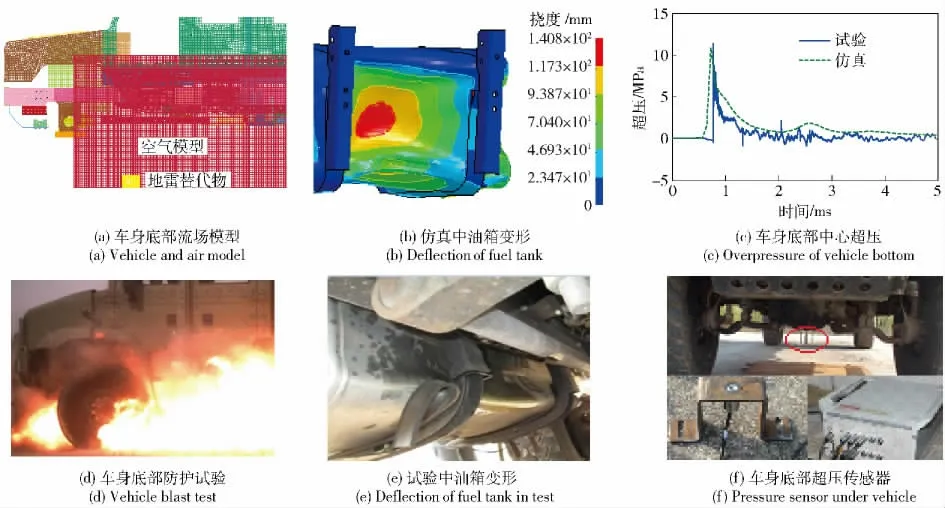
图1 某防护型车辆底部结构仿真分析Fig.1 Numerical analysis of protective vehicle structure

为了验证仿真分析的准确性，进行了地雷爆炸环境下该车辆的验证试验(见图1(d))。试验中，车辆底部的超压传感器(见图1(f))所测量的冲击波超压时间历程曲线与仿真结果吻合度较高(见图1(c))。对比仿真与试验结果，车辆底部结构及其零部件的破坏形态近似，如仿真与试验中油箱(见图1(b)、图1(e)，油箱是变形最严重的部件)变形量均为140 mm. 综上，通过试验验证，仿真精度满足工程需求，结合ALE 与FSI 算法，能准确模拟地雷爆炸环境下车辆底部防护结构的响应。

2 车辆底部结构优化方法

2.1 帕累托最优原理

帕累托最优［11］最早应用于经济学，以图2的双目标最小值问题为例，x3占优于x4、x5(x3的目标函数值均小于x4、x5);x1与x2占优于x3、x4、x5，故x1与x2属于该优化问题的帕累托解集(图2中粗实线)，当优化目标个数大于2 时，帕累托解集为空间曲面。引入标准边界交叉(NBI)法［12］继续对帕累托解集进行寻优。

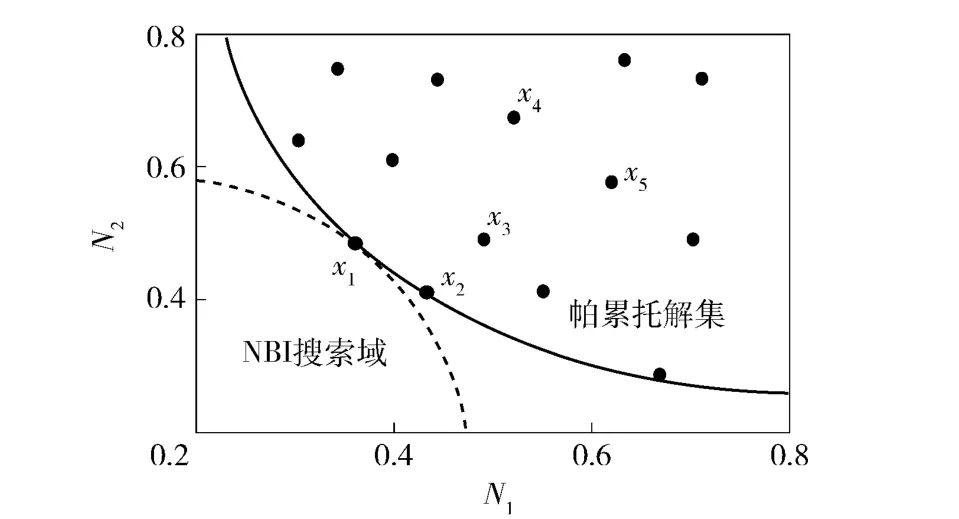
图2 帕累托最优原理Fig.2 Pareto optimality

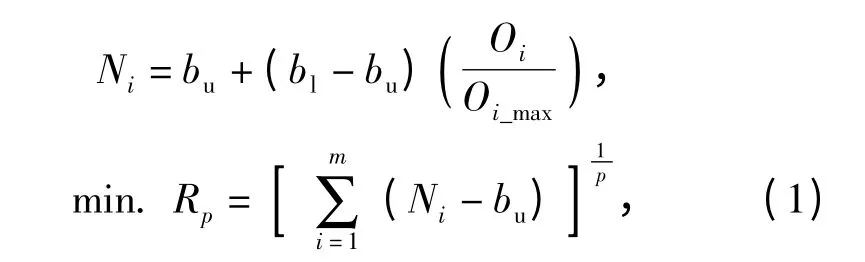
式中:Ni为第i 个优化目标帕累托解的标准化结果;bu、bl是标准化边界的上、下边界;Oi是第i 个目标的帕累托解;Oi_max是第i 个目标的帕累托解集中的最大值;m 为目标函数的个数;在多维空间中，常用的搜索半径Rp可以选用R1、R2和R+∞(p =1，2 和+∞)，本研究中使用R2. 通过NBI 搜索域公式(1)式计算帕累托解集的搜索半径。本算例中，由于R2(x1)最小，故x1是最优方案。

2.2 参数筛选

对于该车辆的底部防护结构设计，需要综合考虑车辆的结构安全与乘员安全，同时减小防护结构对车辆机动性能的影响。以车辆底部防护结构的质量m、比吸能E 和驾驶室地板的变形挠度D、冲击加速度a 为该结构优化设计的4 个目标函数。该车辆底部防护结构为V 型设计，在实际工程设计中，其结构的形状、厚度和角度(V 型结构的卸能角对防护性能影响较大)等因素尤为关键，如图3(a)所示，设底部防护结构的几何尺寸Lz1、Lz2、Lz3、Ly1、Ly2以及板1、2、3 的厚度T1、T2、T3为初始设计变量(初始参数见表1)。利用仿真分析可得到目标函数初始值m、D(见图4(a))、a 和E(见图4(b)).

利用Plackett-burman 试验的采样，建立样本量为12，因子数为8，水平数为2 的S12(28)的参数筛选试验。结合方差分析［13］(ANOVA)方法得到出8 个设计变量分别对4 个目标函数的贡献率(见图3(b)为4 个目标函数贡献率的累计)。为了缩减样本空间，排除了设计变量中贡献率较低的板2 厚度T2，以及底部防护结构y 方向的几何尺寸变量Ly2与Ly1.

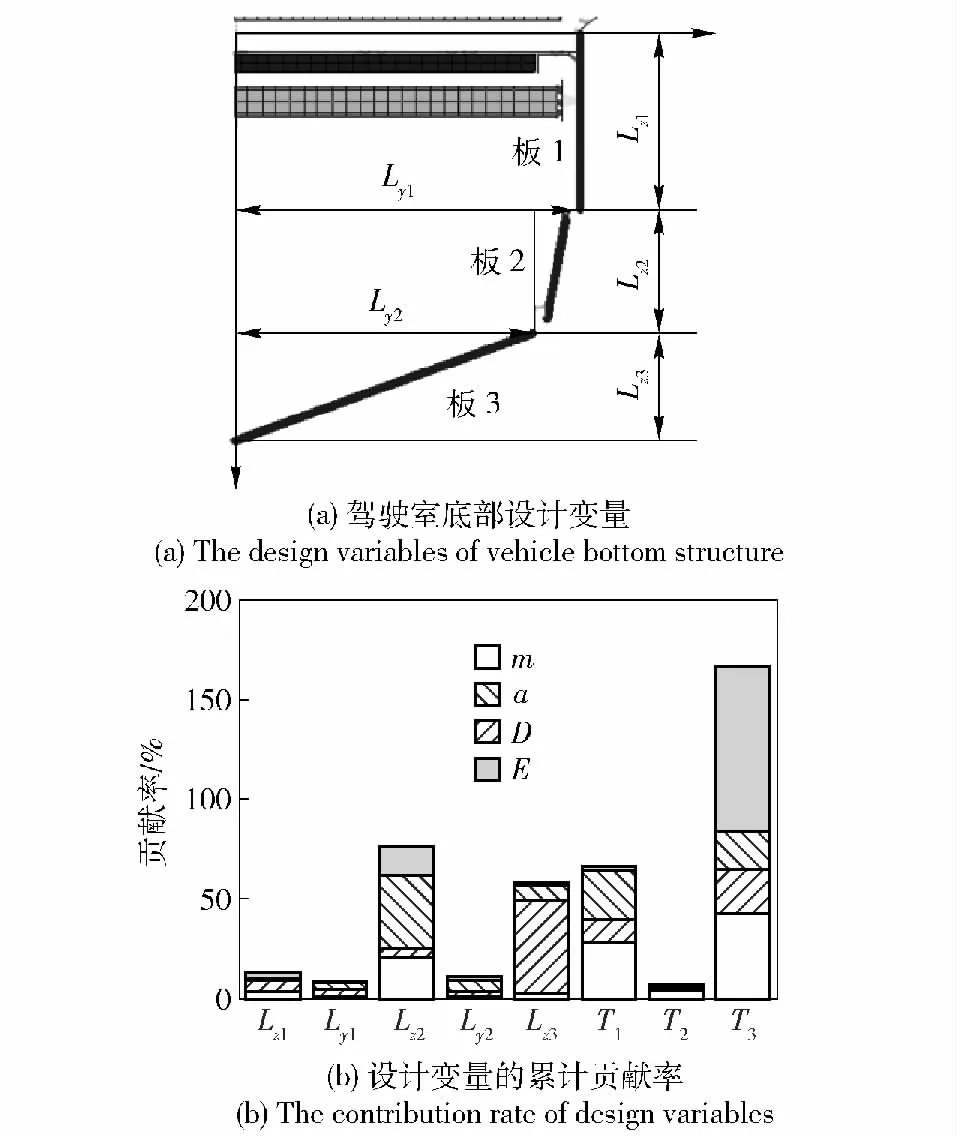
图3 底部结构初始设计变量及其贡献率Fig.3 The design variables of vehicle bottom structure and contribution rate

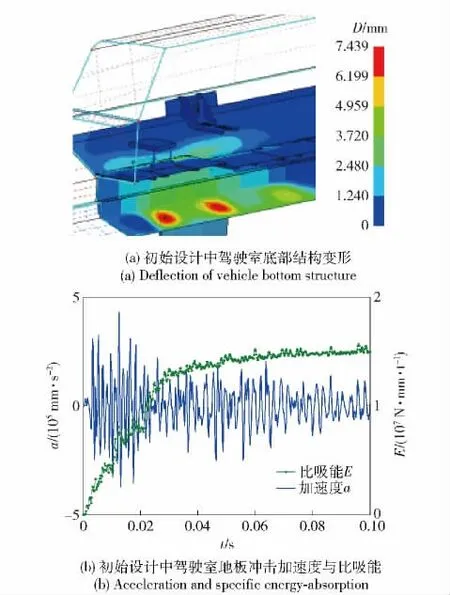
图4 车辆底部结构响应Fig.4 The response of vehicle bottom structure

表1 底部结构设计变量及响应Tab.1 The design variables and responses of bottom structure

2.3 优化数学模型

在该车辆底部防护结构设计中，m、D 和a 应取极小值，比吸能E 取极大值，从而吸收更多的冲击能量，该优化设计的数学模型为

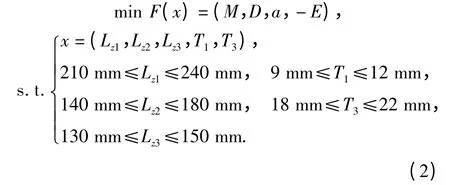
模型应考虑5 个设计变量对目标函数的交互作用，建立因子数为5、水平数为5 的正交中心复合试验S43(55). 根据所得的43 组仿真结果，利用高维模型拟合(HDMR)法［14］的2 阶展开式(3)式，建立m、D、a 和E 的4 个目标的响应面函数。

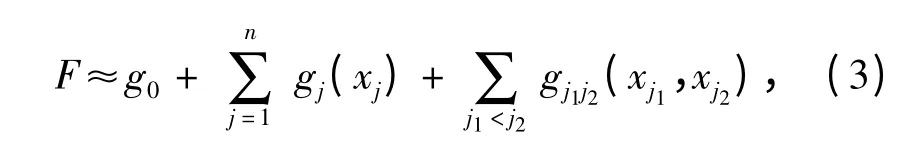
式中:n 代表设计变量的个数;g0是常数项;gj(xj)为1 阶项，表示设计变量对目标函数的独立影响，j=1，2，…，n;gj1，j2(xj1，xj2)为2 阶项，代表设计变量间的耦合作用，j1，j2=1，2，…，n.

3 优化结果分析

3.1 帕累托解集

利用多目标遗传算法［15-16］(MOGA)对车辆底部结构的优化数学模型进行求解，由于该数学模型为4 维多目标优化问题，为了通过帕累托解集描述其空间曲面，求解过程中，设置帕累托解个数为500 个，遗传代数为50 代，每代精英数量为样本空间的10%，变异率为0.01. 最终得到4 个目标函数优化后所对应的帕累托解Om、OD、Oa和OE(见表2以及表3中蓝色的点).

3.2 最优设计方案

由于所得到的帕累托解集维数较高，工程实际中很难通过该空间曲面直接选取合适的设计方案，引入NBI 算法继续在帕累托解集中搜索车辆底部防护结构的最优设计方案。设标准化边界bu=0.2，bl=1(见(4)式)，使得标准化后的帕累托解集中于0.2 ～1 的空间边界内(见表3，为了便于显示帕累托解集，调整了坐标系的刻度)。

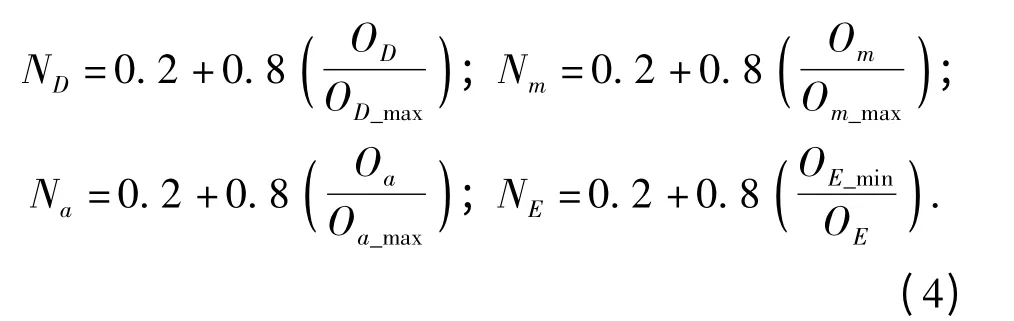
在帕累托解集中，采用不同的优化策略可得到不同的优化设计方案。在该工程实际中，4 个优化目标同等重要(权重相同)，结合(1)式、(4)式，计算出500 组帕累托解的搜索半径R2，其中第52 组R2最小(见表2)，因此第52 组解即为协调了4 个目标函数所得到的最优设计方案(对应表3红点)。

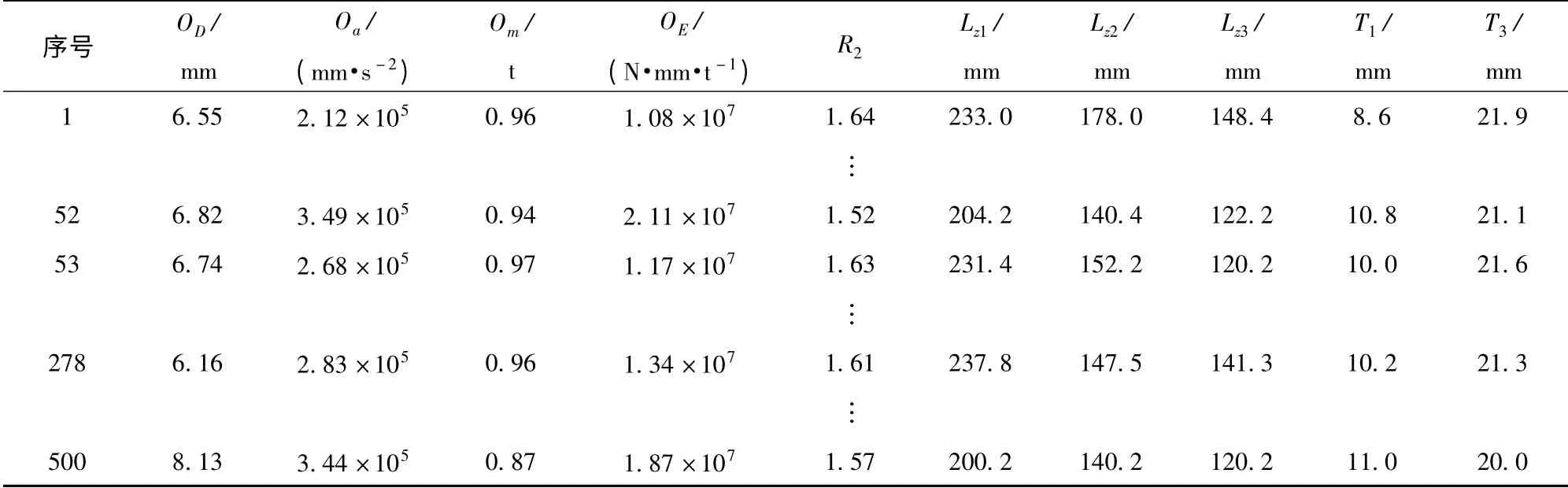
表2 第50 代帕累托解集(部分)及设计参数Tab.2 The 50th generation Pareto set and design variables

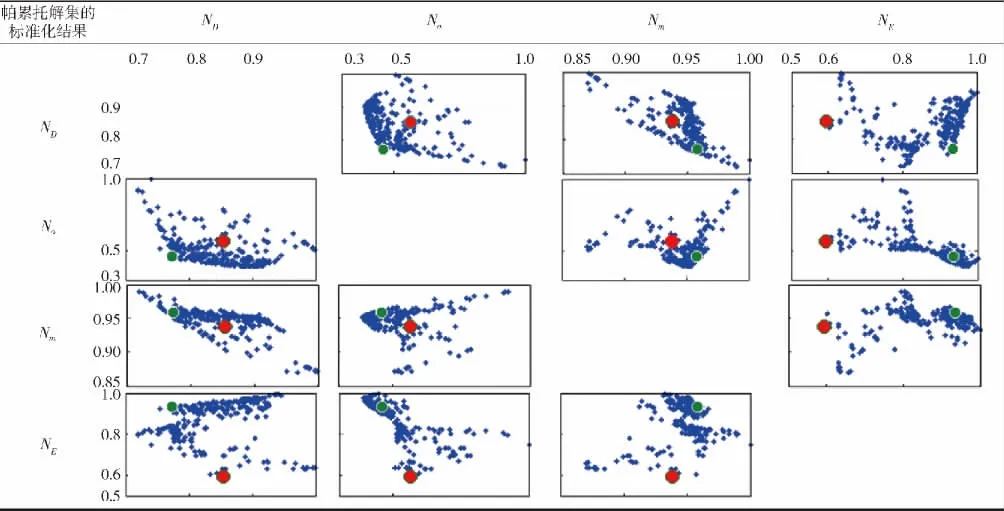
表3 帕累托解集空间曲面及最优设计方案Tab.3 The spatial curved surface of Pareto optimal front and the ideal solution

该优化结果(最优设计方案)是由响应面模型预测所得，为了验证优化结果的准确性，利用经试验标定的仿真模型对其进行检验，仿真值与优化预测结果的相对误差在5%以内(见表4)，响应面模型有较高的预测精度，所得到的最优设计方案真实可信。最优设计方案在底部结构质量Om不变的情况下，驾驶室地板变形挠度OD缩小了8.4%、驾驶室地板冲击加速度峰值Oa缩小了19.2%(见图5)、底部防护结构比吸能OE增加了34.3%(见图6).

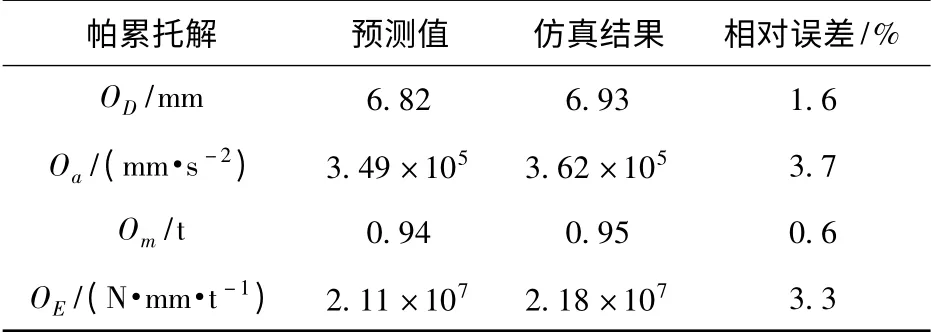
表4 响应面模型的预测精度Tab.4 Prediction accuracy of response surface model

3.3 优化策略影响

在底部防护结构的设计中，如只考虑最大限度地减小驾驶室地板的冲击加速度Oa与变形OD(Om、OE权重为0)，则第278 组帕累托解(对应表3绿点)为优化设计方案。在表3的ND-Na子图中，绿点比红点更靠近坐标原点。相比初始设计，第278 组解Oa缩小了34.5%，OD减小了17.2%，优于第52 组解(见表2);但使用该优化策略将导致底部防护结构的质量Om相比初始设计增加了2.3%(22 kg)，底部结构比吸能OE相比初始设计减小了16.6%.

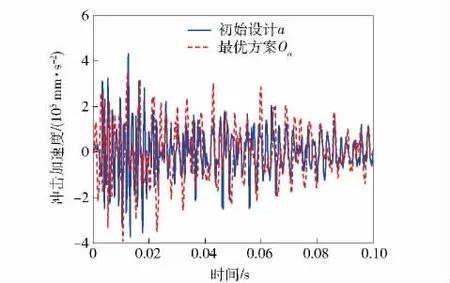
图5 优化前后驾驶室地板冲击加速度对比Fig.5 Comparison of cab floor accelerations of before and after optimization

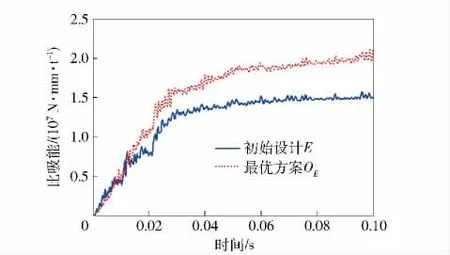
图6 优化前后车辆底部防护结构比吸能对比Fig.6 Comparison of specific energy-absorptions before and after optimization

根据帕累托最优原理，第52 组解、第278 组解与其他的498 组帕累托解集均可视为该车辆底部防护结构的优化策略，这些帕累托解集的一个目标或多个目标优于初始设计，应结合工程实际需求，进行合理选择。

4 结论

本文基于帕累托最优方法，在车辆底部防护结构优化设计中，通过验证试验、仿真分析、参数筛选和HDMR 法，建立了该结构优化设计的准确响应面模型，最终通过多目标遗传算法得到了该设计的帕累托解集，讨论了不同优化策略对各目标函数的影响，得出以下结论:

1)经试验验证，结合ALE 与FSI 算法，能准确模拟地雷爆炸环境下车辆底部防护结构的响应，从而减少设计周期与试验成本。

2)通过参数筛选，在车辆底部防护结构的形貌设计变量中，z 向几何尺寸相对于y 向尺寸的变化，对车辆底部的防护性能影响更大。

3)通过帕累托最优能协调各目标间的矛盾关系，本文在帕累托解集的基础上，引入NBI 算法，提出了底部防护结构的最优设计方案，该方案在不增加结构质量的情况下，能显著提高车辆底部防护性能。

References)

［1］李红勋，谭柏春，贾楠，等. 美军战术轮式车辆发展策略研究［J］. 军事交通学院学报，2012，14(10):84 -87.LI Hong-xun，TAN Bai-chun，JIA Nan，et al. Research on US military tactic wheeled vehicle strategy［J］. Journal of Military Transportation University，2012，14(10):84 -87.(in Chinese)

［2］Ramasamy A，Hill A M，Hepper A E，et al. Blast mines:physics，injury mechanisms and vehicle protection［J］. Journal of the Royal Army Medical Corps，2009，155(4):258 -264.

［3］Sun J L，Vlahopoulos N，Stabryla T J，et al. Blast event simulation for a structure subjected to a landmine explosion，2006-01-0931［R］. New York:SAE Internationa，2006.

［4］Fatt M，Palla L. Analytical modeling of composite sandwich panels under blast loads［J］. Journal of Sandwich Structures and Materials，2009，11(4):357 -380.

［5］Grujicic M，Marvi H，Arakere G，et al. The effect of up-armoring of the high-mobility multi-purpose wheeled vehicle (HMMWV)on the off-road vehicle performance［J］. Multidiscipline Modeling in Materials and Structures，2010，6(2):229 -256.

［6］王飞，陈卫东. 爆炸冲击载荷作用下板壳结构数值仿真分析［J］.强度与环境. 2010，37(4):37 -39.WANG Fei，CHEN Wei-dong. The numerical simulation analysis of the shell structure subjected to contact explosion［J］. Structure＆ Environment Engineering，2010，37(4):37 -39.(in Chinese)

［7］Dharmasena K，Wadley H，Xue Z，et al. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading［J］. International Journal of Impact Engineering，2008，35(9):1063 -1074.

［8］韩守红，吕振华. 军车驾驶室结构抗爆炸特性的数值仿真［C］∥第十届全国冲击动力学学术会议论文摘要集. 太原:中国力学学会，2011.HAN Shou-hong，LYU Zhen-hua.Numerical simulation of protective vehicle under blast wave［C］∥The International Symposium on Impact Dynamics-2011. Taiyuan:Chinese Society of Theoretical and Applied Mechanics，2011.(in Chinese)

［9］NATO. NSA/0533-LAND/4569 Protection levels for occupants of logistic and light armored vehicles［S］. Brussels:NATO，2004.

［10］李利莎，谢清粮，郑全平，等. 基于Lagrange，ALE 和SPH 算法的接触爆炸模拟计算［J］.爆破，2011，28(1):19 -27.LI Li-sha，XIE Qing-liang，ZHENG Quan-ping，et al. Numerical simulation of contact explosion based on lagrange ALE and SPH［J］. Blasting，2011，28(1):19 -27.(in Chinese)

［11］An H G，Green D E，Johrendt J. A hybrid-constrained MOGA and local search method to optimize the load path for tube hydroforming［J］. International Journal of Advanced Manufacturing Technology，2012，60(9/10/11/12):1017 -1030.

［12］Das I，Dennis J E. Normal-boundary intersection:a new method for generating the Pareto surface in nonlinear multicriteria optimization problems［J］. SIAM Journal on Optimization，1998，8(3):631 -657.

［13］Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates［J］. Mathematics and Computers in Simulation，2001，55 (1/2/3):271 -280.

［14］Chowdhury R，Rao B N，Meher P A. High dimentional modelrepresentation for reliab representation for reliability analysis［J］.Communication in Numerical Method in Engineering，2009，25:301.

［15］郝亮，徐涛，崔健，等. 参数化诱导槽设计的吸能盒结构抗撞性多目标优化［J］. 吉林大学学报:工学版，2013，43(1):39 -44.HAO Liang，XU Tao，CUI Jian，et al. Multi-objective optimization for crashworthiness of crash box with parameterized inducing groove［J］. Journal of Jilin University:Engineering and Technology Edition，2013，43(1):39 -44.(in Chinese)

［16］丁炜琦，田程，范子杰. 基于代理模型的大客车结构动态特性多目标优化［J］. 汽车工程，2012，34(12):1072 -1075，1093.DING Wei-qi，TIAN Cheng，FAN Zi-jie. Multi-objective optimization on the dynamic characteristics of bus structure based on surrogate model［J］. Automotive Engineering，2012，34(12):1072 -1075，1093.(in Chinese)