不同跨径组合的三跨连续梁的模态分析试验

罗川舟， 袁向荣(广州大学 土木工程学院，广东 广州 510006)



·计算机技术应用·

不同跨径组合的三跨连续梁的模态分析试验

罗川舟， 袁向荣
(广州大学 土木工程学院，广东 广州 510006)

分析计算三跨等截面等跨连续梁的固有频率和振型，探讨不同跨径组合三跨连续梁振型的区别，并讨论冲击系数的取值。用Midas有限元软件进行分析计算，采用槽型梁作为连续梁模型，以钢辊轴作为支承，为并用DASP模态分析设备对试验模型进行模态分析，得到不同跨径组合下连续梁的前三阶频率及其振型，并将试验结果与Midas计算结果进行对比，证实振型变化的真实性。结果表明，第二、三阶振型随着跨径组合的变化会出现转折，支座处振型的曲率发生变化；考虑跨中支座正弯矩效应时，冲击系数按照《桥规》采用基频计算；考虑中支座负弯矩效应时，冲击系数应采用第二或第三阶频率计算。

连续梁； 振型； 冲击系数； 有限元分析； 模态分析

0 引 言

《公路桥涵设计通用规范》(以下简称《桥规》)[1]4.3.2第4条规定，汽车荷载的冲击力标准值为汽车荷载标准值乘以冲击系数μ。第5条规定，μ可按下式计算:

式中,f为结构基频(Hz)。

冲击系数直接关系到汽车冲击力的取值，《桥规》的冲击系数仅由连续梁的固有频率一个参数所控制。关于如何计算冲击系数这方面的研究主要包括两类，①根据车桥耦合振动计算研究冲击系数[2-4]；②根据桥梁动载试验实测数据，研究冲击系数的取值[5-8]。相关的研究表明，计算分析或实测所得冲击系数大多比按规范规定的计算值要大，此现象在连续梁中支座位置尤为突出。其原因之一是，对于梁的不同控制截面起主要作用的模态不一样，在计算冲击系数是仅考虑桥梁基频是不合理的[9]。因此，对连续梁桥进行完整的模态分析是很有必要的。计算分析三跨连续梁的固有振动，通过有限元计算及试验分析不同跨径组合三跨连续梁的前三阶频率及振型改变，为今后连续梁桥的动力特性研究提供一定的参考价值。

1 三跨连续梁的弯曲固有振动分析[10]

图1表示三跨连续梁的一般情形，为了排除近似计算、各种参数的影响，这里采用等截面连续梁，假设每跨连续梁具有均匀分布的质量和刚度。按Euler-Bernoulli梁理论，第S跨的第n阶振型函数为

φns(x)=Anssinαnsx+Bnscosαnsx+

Cnssinhαnsx+Dnscoshαnsx

根据三跨连续梁的边界条件以及数学推导，可得三跨连续梁的固有振动频率为，

前三阶振型图如图2所示。

图1 三跨连续梁的一般形式

采用Midas有限元软件建立试验梁的有限元分析模型，试验槽型梁的横截面如图3所示，梁长5.4 m。通过数字图像处理技术，对试验梁进行测试[11]，得到其材料参数取值如下：弹性模量E=70 GPa，容重Dens=28 kN/m3。

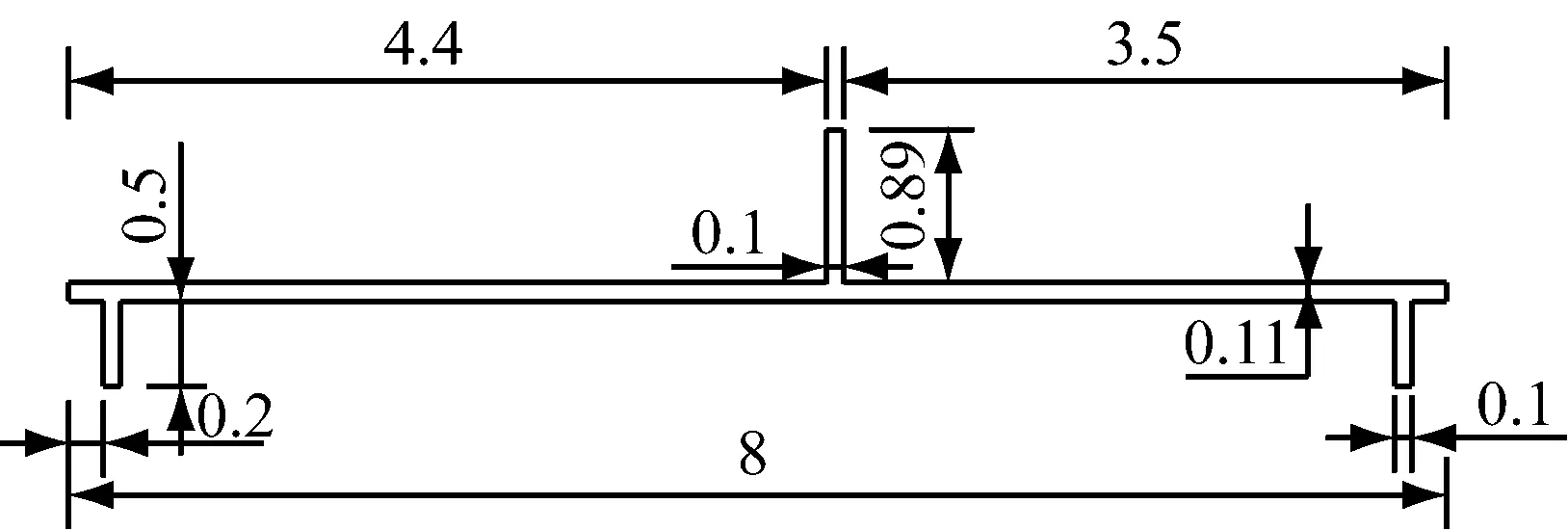
图4为三等跨等截面连续梁Midas Civil有限元计算模型，通过计算分析，并将所得前三阶频率、振型与图2的精确解相比较。结果如表1和图5所示。

图4 有限元分析模型

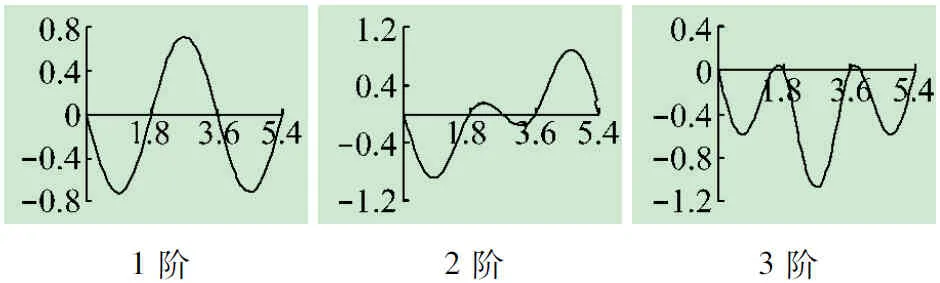
1阶2阶3阶

图5 三等跨连续梁有限元分析的前三阶模型

由表1可以看出，由于计算过程的近似取值，有限元计算的频率值与理论精确解值存在一定的误差，其相对误差不大于7%，在误差允许范围内。对比图2与图5可知，三等跨等截面连续梁的有限元分析振型与理论振型基本保持一致。因此，利用此有限元模型的计算结果为试验提供依据，是较为真实可靠的。

2 三不等跨等截面连续梁的弯曲固有振动分析及试验

2.1 弯曲固有振动分析

对三跨连续梁的各个支座进行编号，如图6所示。通过Midas Civil软件建立有限元计算模型，分别改变1、2号支座的位置得到不同跨径组合的三跨连续梁模型，并计算相应的频率及振型。

为使有限元分析模型与试验条件相一致，在上述模型中，以一个1.274 N的集中荷载代替加速度传感器本身的重力，加在各桥跨相应位置。在支座位置改变的同时，并调整集中荷载的位置。不同跨径组合三跨连续梁有限元分析前三阶模态的频率值如表2所示。

表2 不同跨径组合固有频率的分析计算值 Hz

2.2 弯曲固有振动试验[12-14]

将实验槽型梁布置成三等跨连续梁，支承方式为钢辊轴，采用外直径为2.5 cm的金属管；采用9个加速度传感器，分别粘合于各跨的四分点和跨中。传感器质量为0.138 kg，简单认为其质量沿梁长均匀分布。

对实验对象的激励方式是锤击法，同时用INY306U智能信号采集处理分析仪采集振动信号，通过BZ2015电荷电压滤波积分放大器处理振动信号，最后在计算机上由DASP模态分析程序自动计算出传递函数，再计算频率响应函数，然后对频率响应函数进行集总平均，之后选择合适的频率定阶，最后进行复模态多自由度拟合，这样就可以得到结构的固有频率及其振型。

如图6所示，将实验对象的1号支座往左移动10 cm，共重复3次上述实验步骤，再将实验对象的2号支座往左移动10 cm，共重复3次上述实验步骤，从而获得不同跨径组合的三跨连续梁的固有频率及其振型。

2.3 试验结果

试验测试频率如表2所示。不同跨径组合各阶振型图如图7～9所示。

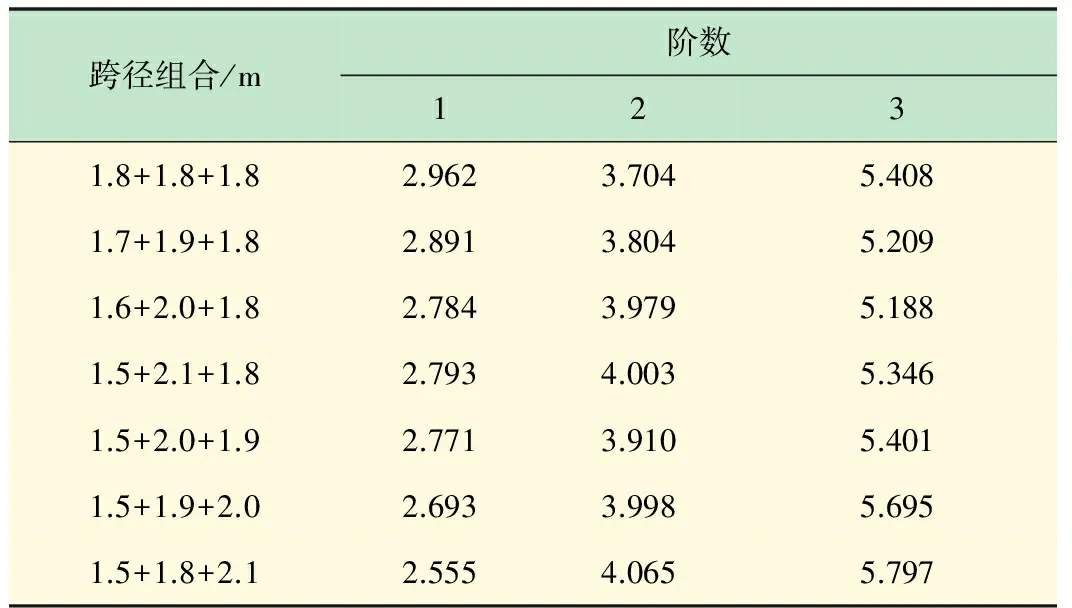
表2 不同跨径组合固有频率的试验测试值 Hz

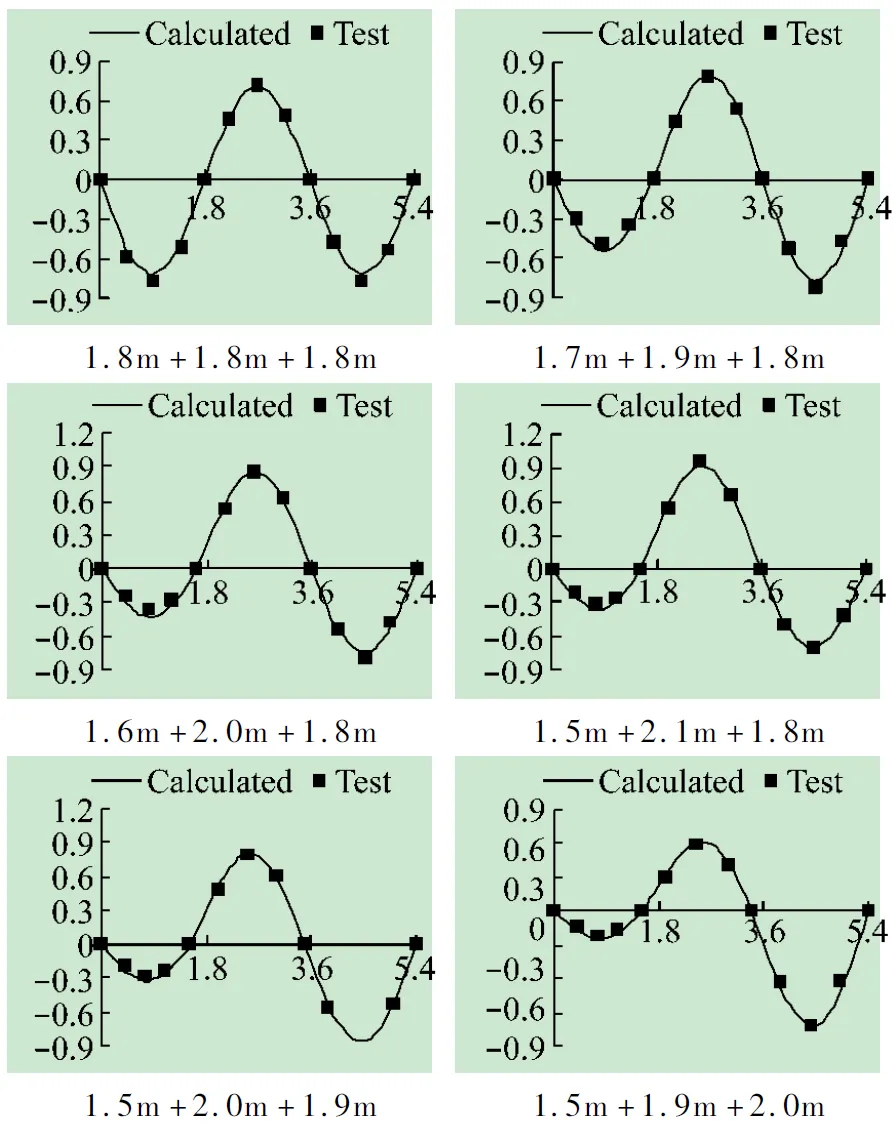
1．8m+1．8m+1．8m1．7m+1．9m+1．8m1．6m+2．0m+1．8m1．5m+2．1m+1．8m1．5m+2．0m+1．9m1．5m+1．9m+2．0m

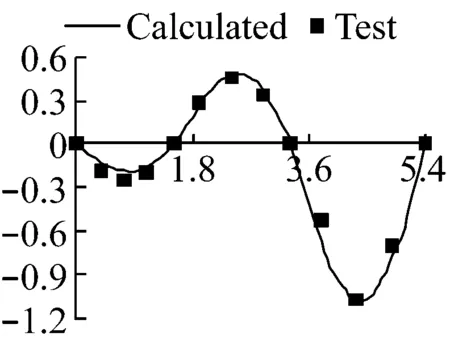
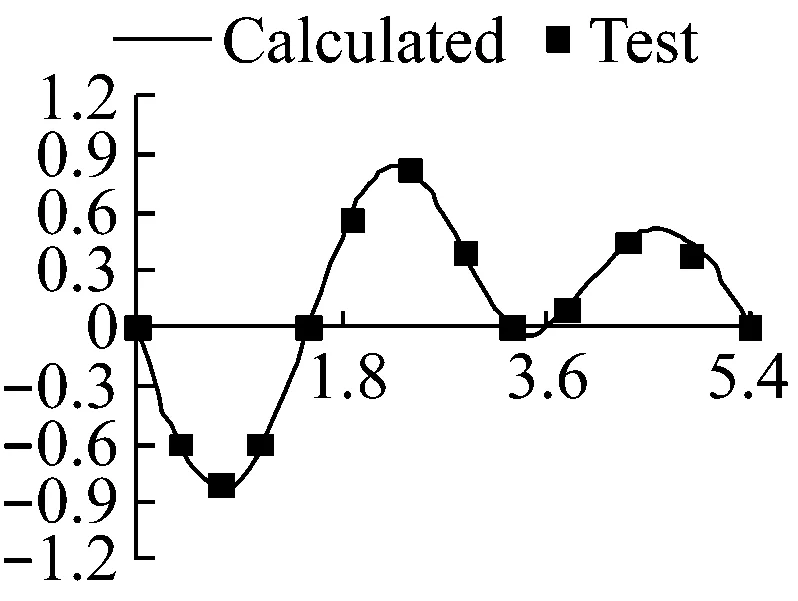
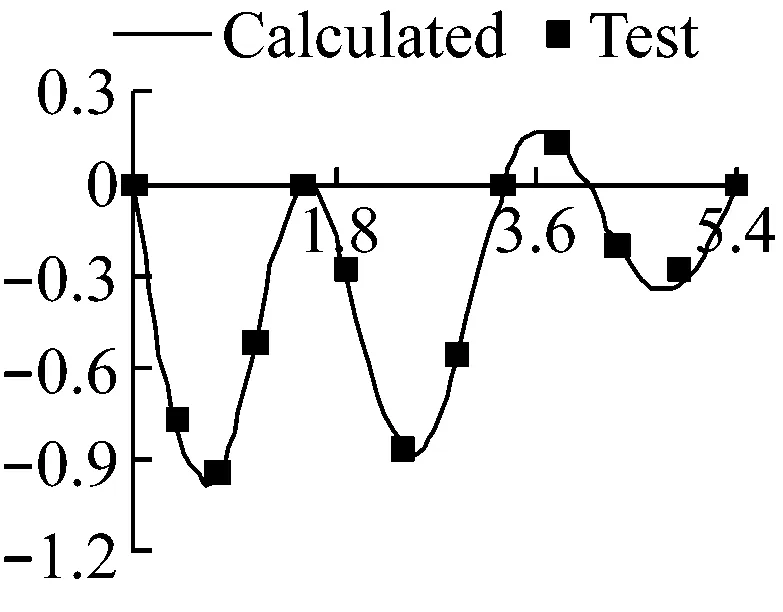
图9 各跨径组合三阶振型图

一阶振型中，等跨时振型相对第2跨跨中正对称，各跨均为半个周期正弦波，波形的振幅相等。随支座位置的改变，1阶振型表现为渐变过程，即跨径大的一跨振幅增大，跨径小的一跨振幅减小，跨径不变的一跨则基本没有变化，总体而言振型无本质变化。

二阶振型中，等跨时振型相对第2跨跨中反对称，第1、3跨为半个周期正弦波，波形振幅相等，方向相反，第2跨为一个完整周期正弦波，波形振幅较两边跨小。随1、2号支座先后往左移动,①第2跨波形首先由左右幅值相等的正弦波渐变为左右幅值不相等的正弦波，最后随跨径减小由完整周期突变为半个周期的正弦波，第3跨波形则由半个周期突变完整周期的正弦波；②2号支座出现反弯点，曲率由0逐渐增大，在第2、3跨跨径接近时达到最大值，类似于两等跨连续梁2阶振型中支点出现反弯的情况。

三阶振型中，等跨时，振型相对第2跨跨中正对称，第1、3跨为一个完整正弦波，幅值相等，第2跨为半个正弦波，幅值较两边跨大。随1、2号支座先后往左移动,①第1跨波形由完整周期突变为半个周期的正弦波，第2跨波形首先由半个周期突变为整个周期的正弦波，随跨径的减小，最后重现突变为半个周期的正弦波，第3跨波形则始终为完整周期的正弦波，并有变为左右振幅相等的趋势；②1号支座先出现反弯点，曲率由0突变至最大值，然后逐渐减小，最后随第2跨波形被压缩，曲率达到最大值；③第3阶振幅与桥跨成反比例关系。

表3为各跨径组合前三阶的有限元分析频率与试验测试频率的相对误差。对比有限元分析结果和试验测试结果可知，随着连续梁支座的位置不断改变，试验梁振型的变化与有限元分析的振型变化趋势基本一致。说明不同跨径组合的三跨连续梁各阶振型的变化是真实的。

表3 有限元计算值与试验测试值的相对差 %

《桥规》条文说明中指出，汽车荷载的冲击系数可表示为：

η=Ydmax/Yjmax

式中：Yjmax为在汽车过桥时测得的效应时间历程曲线上，最大静力效应处量取的最大静力效应值；Ydmax为在效应时间历程曲线上最大静力效应处量取的最大动效应值。

梁弯曲时，距中性层距离为y的纤维应变为：

ε=yυ″

式中，υ″为中性层的曲率[12]。

根据力学原理，有：

故弯矩M与曲率υ″为正比关系，即较大的动弯矩只会发生在振型曲率的较大处。

当考虑支座处负弯矩效应时，对于不同跨径组合三跨连续梁，需按不同的阶数频率进行计算。三跨连续梁一跨的跨径较另外两跨小，当跨径较大两跨的跨径处于0.85～1.00范围内，其所在的2号支座此时应按第二阶频率计算冲击系数；当跨径较小一跨与临跨跨径比处于0.8～0.9范围内，其所在的1号支座此时应按第三阶频率计算冲击系数。

3 结 语

通过计算分析及试验测试可以得出以下结论：

(1)随支座的位置改变，各阶振型均发生变化，支座处第二、三阶振型发生转折，如图8、9；二阶振型中2号支座出现反弯点，曲率由0逐渐增大，在第2、3跨跨径接近时达到最大值，类似于两等跨连续梁2阶振型中支点出现反弯的情况；三阶振型中1号支座先出现反弯点，曲率由0突变至最大值，然后逐渐减小，最后随第2跨波形被压缩，曲率达到最大值。

(2)不同跨径组合的三跨连续梁，其第一阶模态对各桥跨的跨中截面动弯矩起主要作用，即最大动弯矩在跨中处，此处的冲击系数也最大，因此考虑各跨跨中正弯矩效应时，冲击系数按照《桥规》采用基频计算是合理的。

(3)考虑支座处负弯矩效应时，则不能只按照基频计算其冲击系数。对于一跨的跨径较另外两跨小的三跨连续梁，应分情况考虑：当跨径较大两跨的跨径处于0.85～1.00范围内，其所在支座此时应按第二阶频率计算冲击系数；当跨径较小一跨与临跨跨径比处于0.8～0.9范围内，其所在支座此时应按第三阶频率计算冲击系数；其他情况，则须采用更高阶频率。

(4)按照振动理论，梁在荷载作用下的动弯矩是其各阶振型的线性组合。对于连续变化跨径比的连续梁冲击系数的进一步确定，可对所采集的各阶振型通过计算机进行叠加，但其准确性还有待探究。

[1] 交通部. 公路桥涵设计通用规范(JTG D60-2004)[S]. 北京：人民交通出版社，2004.

[2] 盛国刚，彭 献，李传习. 连续梁桥与车辆耦合振动系统冲击系数的研究[J]. 桥梁建设， 2003(6)：5-7.

[3] 张元文，姜长宇. 公路连续梁桥冲击系数的探讨[J]. 山西建筑， 2008，34(14)：347-348.

[4] 桂水荣，陈水生，任永明. 先简支后连续梁桥车辆冲击系数影响因素研究[J]. 公路交通科技， 2011，28(5)：54-60.

[5] 施尚伟，赵 剑，舒绍云. 梁桥冲击系数实测值与规范取值差异分析[J]. 世界桥梁， 2010(2)：80-82.

[6] 许士强，陈水生，桂水荣. 公路桥梁汽车冲击系数对比研究[J]. 工程建设与设计， 2006(12)：73-75.

[7] 孙伟良. 多跨先简支后连续钢筋混凝土空心板桥梁冲击系数研究[J]. 石家庄铁道学院学报，2007，20(2)：52-56.

[8] 王海城，施尚伟. 桥梁冲击系数的影响因素及偏差成因[J]. 重庆交通大学学报(自然科学版)，2007，26(5)：25-28.

[9] 姜长宇，张 波. 关于公路桥梁冲击系数的探讨[J]. 公路工程与运输，2005，148：38-41.

[10] 宋一凡. 公路桥梁动力学[M]. 北京：人民交通出版社，2000.

[11] 袁向荣. 边缘识别的正交多项式拟合及梁变形检测[J]. 实验室研究与探索，2013，32(10)：11-13.

[12] 徐文峰，袁向荣. DASP系统在连续梁模态分析中的应用[J]. 工程与试验，2011，51(4)：58-59.

[13] 袁向荣，刘 敏，蔡卡宏. 采用数字图像边缘检测法进行梁变形检测及破损识别[J]. 四川建筑科学研究，2013，39(1)：68-70.

[14] 赵汗青，高兴海，李海燕. 悬臂梁振动参数的实验测试方法分析与比较[J]. 实验室研究与探索，2009，28(12)：47-49.

[15] 袁向荣. 基于连续梁振动分析的桥梁冲击系数研究[J]. 四川建筑科学研究，2013，39(4)：190-194.

[16] 田玉梅，何东坡，徐 岩. 桥梁冲击系数的探讨[J]. 东北林业大学学报，2001，29(1)：88-89.

[17] 单 炜，张宏祥，李玉顺.公路桥梁检测技术[M]. 哈尔滨：东北林业大学出版社，2005.

Modal Analysis Test for Three-unequal-span Continuous Beams

LUOChuan-zhou,YUANXiang-rong
(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

This paper analyzes the natural frequency and mode of vibration of three-unequal-span which has the same section and span, discusses the difference of the three-unequal-span when it has different spans, and discusses further the values of impact factor. The finite element analysis software Midas and the DASP equipment are respectively used for modal analysis to obtain the first three vibration modes and frequencies of the continuous beam on different spans. Compared Two results are compared, and it can confirm the authenticity of the vibration mode change. The results demonstrate that (1) with the spans change, the vibration mode will turn and the curvature of vibration mode will change; (2) when the effect of positive bending moment is steady, the fundamental frequency should be used that shown in the General Code to calculate the impact factor; (3) when the effect of negative bending moment is at middle fulcrum, the 2nd or 3rd frequencies should be used to calculate the impact factor.

continuous beams; vibration mode; impact factor; finite element analysis; modal analysis

2014-05-19

国家自然科学基金(51078093,51278137)，广州市科技计划项目(12C42011564)；广州大学土木工程学院硕士研究生创新实验项目

罗川舟(1988-)，男，广东阳江人，硕士生，目前从事桥梁工程、图像监控研究。

Tel.:15017532191；E-mail:sdljlcz1@163.com

袁向荣(1957-)，男，河北故城人，博士，教授，目前从事桥梁工程、图像工程研究。

Tel.:020-39366669；E-mail: rongxyuan@163.com

U 441.3

A

1006-7167(2015)02-0096-05