方框图系统模型的分析与教学探讨

杨　金，蒋先伟，王菲菲，鲁世斌

(合肥师范学院 电子信息工程学院,安徽 合肥 230601)



方框图系统模型的分析与教学探讨

杨金，蒋先伟，王菲菲，鲁世斌

(合肥师范学院 电子信息工程学院,安徽 合肥 230601)

[摘要]线性微分方程和方框图是信号与系统中两种重要的系统模型。针对大多数教科书对于由微分方程绘制方框图的讲解不够完善，造成学生难以理解的问题，通过总结和对比已有的方法使学生容易理解和掌握方框图的绘制，从而提高了教学质量并取得了良好的教学效果。

[关键词]方框图；系统模型；线性微分方程

信号与系统课程是高等学校电子信息类、自动化的专业基础课，是一门理论性和系统性都很强的专业必修课，几乎所有的工程技术领域都会涉及到信号与系统问题，为后续数字信号处理、通信原理等课程里面的信号与系统分析做好准备[1-4]。

科学的每一分支都有自己的一套“模型”理论，在模型的基础上可以运用数学工具进行研究。为便于对系统进行分析，同样需要建立系统的模型。所谓模型，是系统物理特性的数学抽象，以数学表达式或具有理想特性的符号组合图形来表征系统特性[5]。

对于信号与系统这门课程中的线性时不变(Linear Time Invariant, LTI)系统，常用线性微分方程和方框图两种模型来表示系统。教科书中对线性常微分方程模型给予了详细地阐述，但是对于方框图模型讲解的比较少，尤其没有讲解如何根据线性微分方程绘制方框图，造成学生难以理解和掌握的问题。而方框图在系统分析和综合中也是一种重要的模型，比如数值仿真软件Simulink就是基于方框图的一种仿真工具[6]。因此，详细总结和阐述由线性微分方程绘制方框图的方法，使学生理解和掌握方框图模型的搭建，具有重要的教学意义。

1方框图系统模型

方框图表示系统模型时，每个方框图反映某种数学运算功能，给出该方框图输出与输入信号的约束条件，若干个方框图组成一个完整的系统。对于线性微分方程描述的系统，它的基本运算单元是相加、倍乘(标量乘法运算)和积分(或微分)。在实际应用中为了抑制突发干扰噪声的影响，通常选择积分运算单元。三种基本运算的方框图及其运算功能如图1所示[5]。

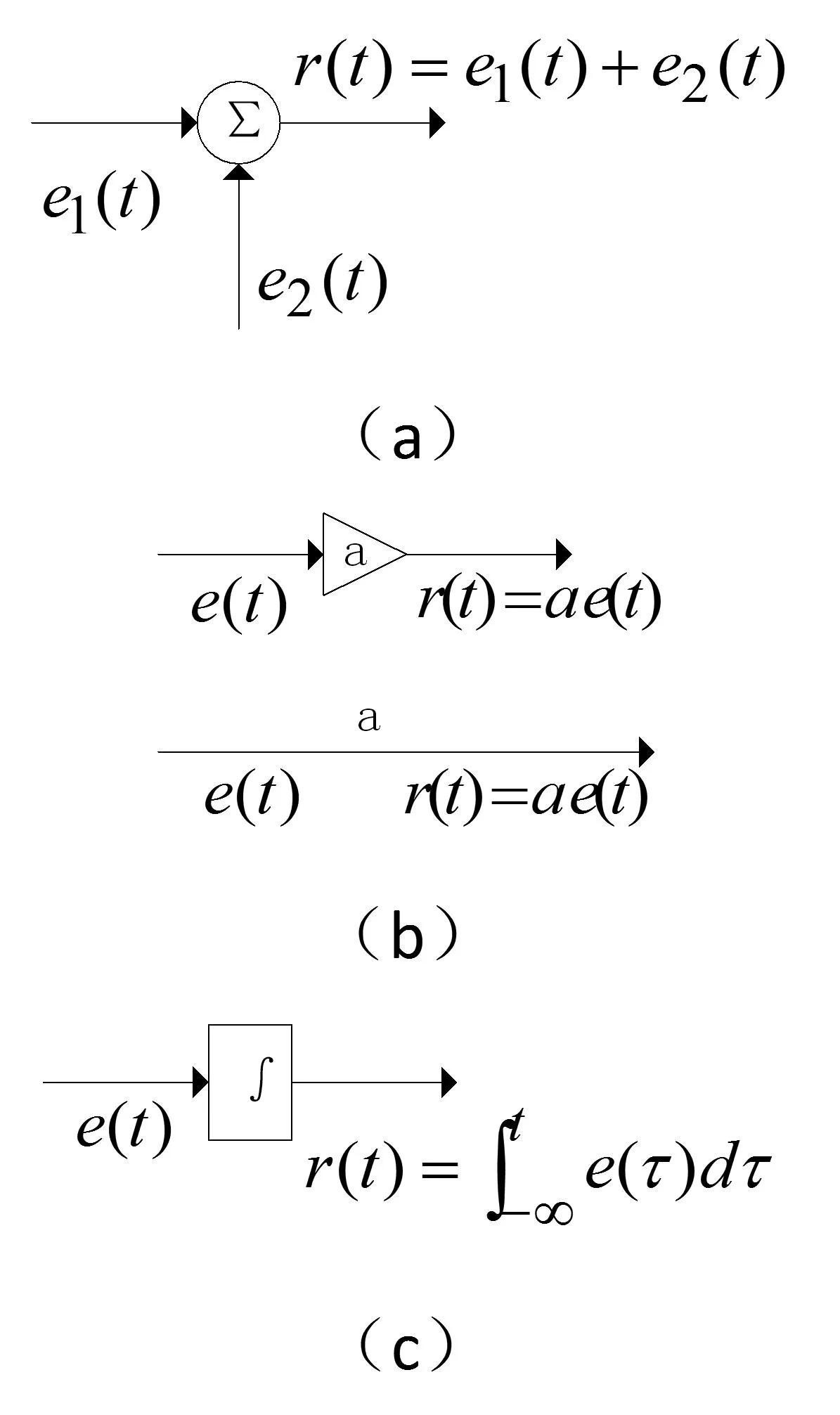
图1　三种基本单元方框图(a)相加(b)倍乘(c)积分

2方框图的绘制

2.1直接积分法

图2　与式(1)对应的方框图

对于简单的一阶微分方程可以直接积分、化简和整理变成积分表达式，然后绘制方框图模型，如式(1)和图2所示。

(1)

积分、化简和整理得

(2)

则方框图模型为图2所示。

2.2中间变量代换法

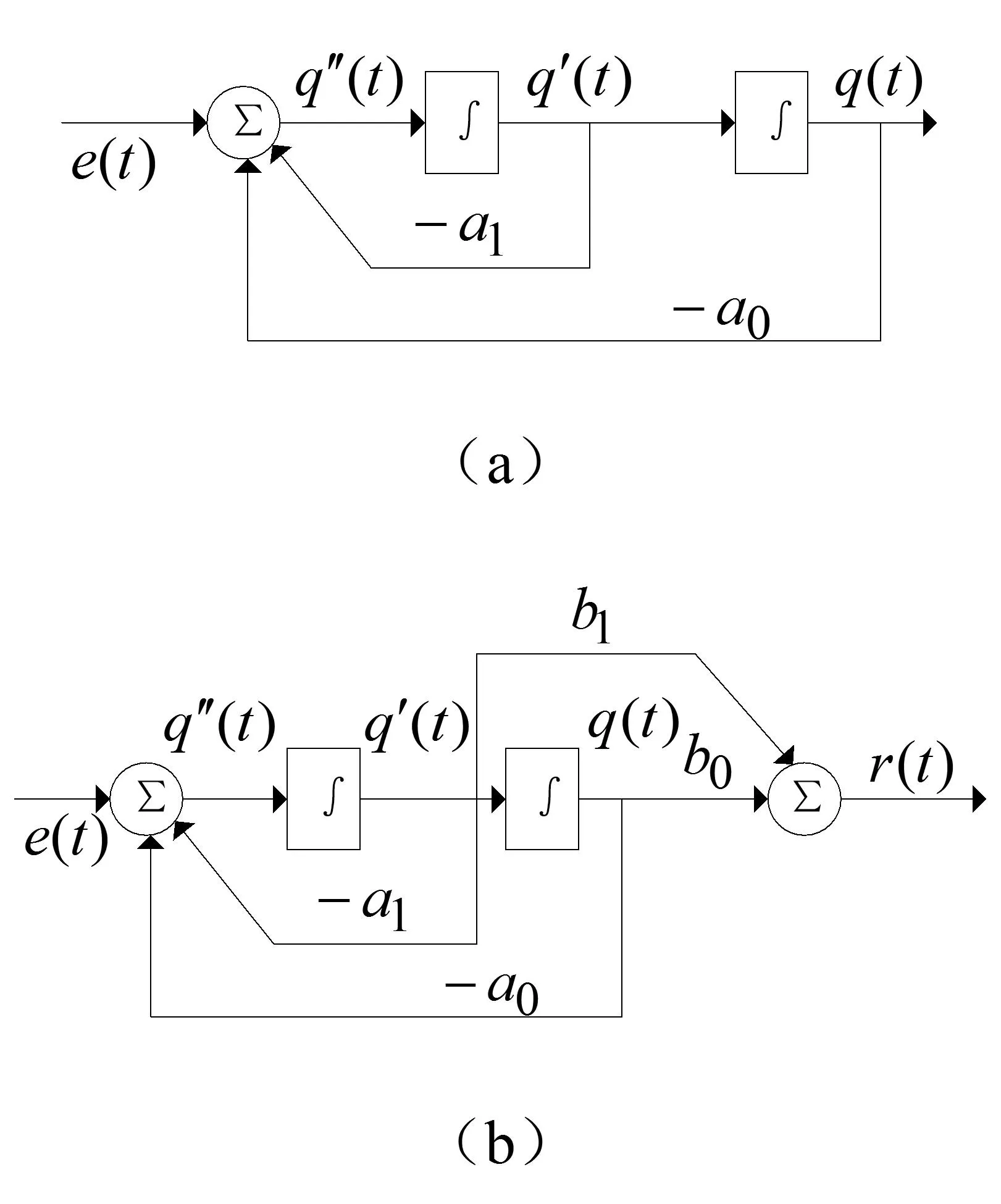
图3　(a) 式(4)的方框图，(b) 式(3)的方框图

直接积分法只适用于激励形式相对简单的一阶线性微分方程，对于激励形式复杂的高阶线性微分方程使用中间变量法比较方便和清晰，如式(3)和图3所示。

(3)

去中间变量q(t)，使q(t)与e(t)满足

(4)

对应的方框图如图3(a)所示，将式(4)代入(3)得

(5)

由式(5)易得

(6)

在图3(a)的基础之上，由式(6)易得图3(b)所示的方框图

2.3子系统交换法

图4　(a) 式(3)方框图，(b) 增加一个加法器，(c) 子系统交换，(d) 去掉微分符号

中间变量代换法要推导公式，有些麻烦，通过观察整个公式推导的过程和图3，会发现其中有一些规律和技巧可以利用，可以不用推导公式，直接绘制方框图。

第一步，由式(3)可以很容易得到图4(a)所示的方框图。

第二步，令

(7)

可以把图4(a)拆分成图4(b)所示的方框图。

第三步，对比图3(a)和图4(b)的右半部分发现它们的拓扑结构是一样的；对比式(6)和式(7)发现它们的系数一样，即可以用图4(b)的左半部分的方框图实现式(6)。因此可以把图4(b)的左半部分和右半部分交换，即把两个子系统交换。实质上，交换后实现的是式(4)和式(6)的组合，即实现了式(3)的方框图模型。

第四步，为了统一使用积分运算，不使用微分运算，可以如图4(d)所示，把微分符号替换掉，得到与图4(b)一样的方框图。

与中间变量法相比，子系统交换法不需要推导公式，只需要直接从公式(3)绘制方框图、增加一个加法器把方框图拆分成左右两部分、交换子系统和去掉微分运算四步就可以绘制成最终的方框图，省去公式推导的麻烦。

3结束语

通过总结和对比直接积分法、中间变量代换法和子系统交换法三种根据微分方程绘制方框图模型的方法，使学生理解和掌握了信号与系统课程中方框图模型的绘制技巧，激发了学生学习的积极性，提高了教学质量，经实际教学验证达到了良好的教学效果。

[参考文献]

[1]黄岚, 马云辉, 陈永海. 《信号与系统》课程教学改革研究-独立学院《信号与系统》课程教学现状分析与探讨[J]. 科技信息, 2009: 641-642.

[2]王大雄, 万东辉, 蒋林华, 雷能玮. 信号系统与信号处理教学改革初探[J]. 湖州师范学院学报, 2011, 33(2): 125-128.

[3]张红燕, 李立礼, 樊东红. 基于MATLAB的信号与系统教学研究[J]. 时代教育, 2011, 1: 18-19.

[4]沈君凤. “信号与线性系统”课程教学方法探索与实践[J]. 中国科教创新导刊，2012, 2: 178-180.

[5]郑君里, 应启衍, 杨为理. 信号与系统(第三版)[M]. 北京: 高等教育出版社，2011.

[6]薛定宇, 陈阳泉. 基于MATLAB/Simulink的系统仿真技术与应用[M]. 北京: 清华大学出版社，2011.

An Analysis on and Teaching Exploration in Block Diagram System Model

YANG Jin, JIANG Xianwei, WANG Feifei, LU Shibing

(SchoolofElectronicandInformationEngineering,HefeiNormalUniversity,Hefei230601,China)

Abstract：Linear differential equation and block diagram are two important system models in the signal and system. However, there are inadequate and imperfect explanations about block diagram drawn with linear differential equations, which makes it difficult for students to understand. This paper summarizes and compares the existing methods which students find easy to understand and grasp the drawing of block diagram so as to increase the teaching quality and achieve the better teaching effect.

Key words：block diagram; system model; linear differential equation

[中图分类号]G64

[文献标识码]B

[文章编号]1674-2273(2015)06-0079-02

作者简介][第一 杨金(1984-)，女，安徽淮北人，讲师，博士，研究方向：电路与系统。

[基金项目]安徽高校省级自然科学研究项目(KJ2015A276);人才科研启动基金(2015rcjj02)；安徽高校省级自然科学研究项目(KJ2014A208)

[收稿日期]2015-07-10