改进的基于闵氏距离的软子空间聚类算法
支晓斌, 高垚琦
(1.西安邮电大学 理学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
改进的基于闵氏距离的软子空间聚类算法
支晓斌1, 高垚琦2
(1.西安邮电大学 理学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
用L1范数和L2范数的加权组合取代基于闵氏距离的软子空间(Minkowski metric based soft subspace, MSC)聚类算法目标函数中所用的Lp范数,导出一个新的MSC的聚类中心计算公式,从而得出一种改进的MSC聚类算法。改进算法使MSC的计算复杂度由O(n2mc)降为O(nmc)(这里n是数据个数,m为数据维数,c是聚类数)。在Iris,breastcancer,Vehicle,User和Wine 5个真实数据上的对比性实验结果显示,改进MSC算法的聚类精度与原MSC的聚类精度相当,但改进算法的运行时间是原MSC运行时间的1/7到1/2。
聚类算法;软子空间;闵科夫斯基距离;加权组合
聚类分析是无监督模式识别的主要组成部分[1]。K-均值(K-means,KM)聚类算法[2]易于实现且简单高效[3],但过分依赖聚类中心点的选取,不能自动进行特征选择。
为了使KM算法能够自动对数据进行特征选择,学者们提出了特征加权K-均值聚类[4]算法及其改进[5],其特征权重可由模糊K-均值聚类算法[6]隶属函数的求解方法得出。软子空间(Soft Subspace, SC)聚类算法[7]可以发现每个类所在的子空间,是特征加权聚类算法的研究热点[8-10]。
SC聚类算法多以欧式距离定义目标函数,限制了算法对数据的适应性。利用p次方距离代替平方距离,可得基于闵氏距离的软子空间聚类(Minkowski Distance Based Subspace Clustering, MSC)算法[9],它对数据的适应性优于基于欧式距离的SC聚类算法,但闵氏指数取一般值的MSC计算复杂度较高,不适合较大数据集。
注意到闵氏指数取值为1和2的MSC效率较高,本文拟将它们进行加权组合,对闵氏指数取值在区间[1,2]上的MSC进行近似,得出一种高效MSC聚类(Efficient Minkowski Distance Based Subspace Clustering, EMSC)算法。
1 EMSC算法描述
设有n个m维数据点组成数据集
X={x1,x2,…,xn}。
EMSC的目标函数定义为
其中隶属度矩阵
聚类中心矩阵
V=(V1,V2,…,Vc),
由c个聚类中心构成;特征权重矩阵
权重因子λ∈[0,1]。
当λ=0时,EMSC退化为SC,而当λ=1时,EMSC退化为基于L1范数的MSC。
EMSC算法通过迭代求解3个问题来最小化其目标函数。
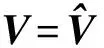
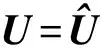
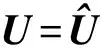
选取加权距离
d(xik,vjk)=
λ|xik-vjk|1+(1-λ)|xik-vjk|2,
可得问题1的最优解,即若
则有uij=1,否则,uij=0;问题2的最优解
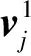
其中
而cardS表示集合S中元素的个数。
EMSC算法的具体步骤可描述如下。
步骤1数据集规范化处理[9]。
步骤2随机初始化聚类中心矩阵V,初始化特征权重矩阵W,使
步骤3计算问题1的最优解,更新隶属度矩阵U。
步骤4计算问题2的最优解,更新聚类中心矩阵V。
步骤5计算问题3的最优解,更新特征权重矩阵W。
步骤6记更新后的聚类中心矩阵为V′,如果满足‖V′-V‖<ε,则停止,否则转到步骤3。
EMSC算法中步骤3、步骤4和步骤5的计算复杂度均为O(nmc),因此EMSC算法的计算复杂度为O(nmct)。EMSC算法与KM和SC两种算法的计算复杂度相当,但远低于改进前的MSC[9]算法,因此,EMSC算法比原MSC算法更为高效。
2 实验结果及分析
将EMSC算法与KM聚类算法和MSC算法分别在5个真实数据上进行对比实验。
2.1 实验设置
从UCI数据库[11]中选取Iris,Breastcancer,Vehicle,User和Wine 5个数据,其相关特性如表1所示。
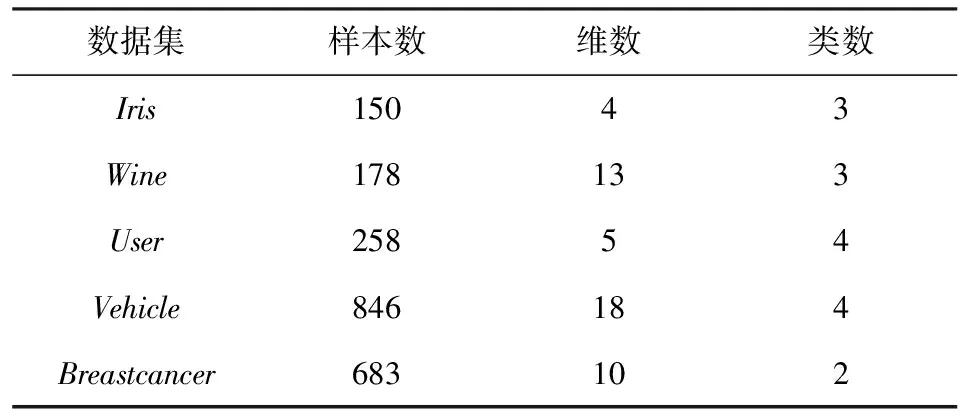
表1 数据描述
用准确度a和运行时间T来衡量聚类算法的性能。准确度定义为
其中nj是数据正确分到第j类的数目。实验用特征加权指数β固定为10。
2.2 精度测试及闵氏指数敏感性分析
针对5个数据集,在闵氏指数p的11个不同取值下,3种聚类算法经10次运算的平均聚类精度分别如表2至表6,其间EMSC算法对应的λ值由
p=λ+2(1-λ)
计算得出。

表2 数据集Iris的聚类精度

表3 数据集Wine的聚类精度

表4 数据集User的聚类精度

表5 数据集Vehicle的聚类精度

图6 数据集Breastcancer的聚类精度
表2至表6显示,MSC算法和EMSC算法在5个数据集上的聚类精度优于KM聚类算法。在Iris,Wine,User和Vehicle 4个数据集上,EMSC算法与MSC算法精度相当。在Breastcancer数据集上,EMSC算法的聚类精度在参数p取1.1~1.5时高于MSC算法的聚类精度。
2.3 运行时间测试
针对5个数据集,在闵氏指数p的11个不同取值下,3种聚类算法经10次运算的平均运行时间分别如表7至表11所示。

表7 数据集Iris聚类耗时

表8 数据集Wine聚类耗时

表9 数据集User聚类耗时

表10 数据集Vehicle聚类耗时

表11 数据集Breastcancer聚类耗时
表7至表11显示,对于所有5个数据集,KM聚类算法是3个算法中效率最高的,所用的运行时间最短。对于所有5个数据集,参数p的大多数取值,EMSC算法的效率要明显优于MSC算法,在运行时间上较MSC有大幅降低。
EMSC算法在聚类精度上与MSC算法相当,而在效率上要远优于MSC算法。
3 结语
将闵氏指数取值为1和2的MSC进行加权组合来对闵氏指数取值在区间[1,2]上的MSC进行近似,提出了高效的MSC的聚类算法EMSC,其计算复杂度与SC算法的计算复杂度相当,远低于闵氏指数取一般值的MSC算法。实验结果表明,EMSC的聚类精度与原MSC(闵氏指数取值在区间[1,2]上)相当,但效率远高于原MSC算法。对于闵氏指数取值在区间[1,2]上的MSC,EMSC是其一个可供选择的高效代替算法。
[1] Jain A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666.
[2] MacQueen J. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. Oakland: University of California Press, 1967: 281-297.
[3] 冯霞,王曙燕,孙家泽. 基于K-means聚类的组合测试用例生成优化算法[J].西安邮电大学学报,2015,19(1):44-48.
[4] DeSarbo W S, Carroll J D, Clark L A, et al. Synthesized clustering: A method for amalgamating alternative clustering bases with differential weighting of variables[J].Psychometrika, 1984, 49(1):57-78.
[5] Huang Z X, Rong H Q, Li Z C, et al. Automated variable weighting in k-means type clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 657-668.
[6] Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum Press, 1981: 95-107.
[7] Chan E Y, Ching W K, Ng M K, et al. An optimization algorithm for clutering using weighted dissimilarity measures[J]. Pattern Recognition, 2004, 37(5): 943-952.
[8] Jing L, Ng M K, Hang J Z. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse date[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026-1041.
[9] Amorim R C, Mirkin B. Minkowski metric, feature weighting and anomalous cluster initializing in K-Means clustering[J]. Pattern Recognition, 2012, 45(3): 1061-1075.
[10] Zhi Xiaobin, Fan Jiulun, Zhao Feng. Robust Local Feature Weighting Hard C-Means Clustering Algorithm[J]. Neurocomputing, 2014, 134: 20-29.
[11] Blake C L, Merz C J. UCI repository of machine learning databases[EB/OL].(1998-07-01)[2015-06-24] .http://www.ics.uci.edu/~mlearn/MLRep-ository.htm.
[责任编辑:瑞金]
A new algorithm for Minkowski metric based soft subspace clustering
ZHI Xiaobin1, GAO Yaoqi2
(1. School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2. School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
An improved Minkowski metric based soft subspace (MSC) clustering algorithm is presented. A weighted combination of theL1 norm andL2 norm is used in the objective function of MSC clustering algorithm to replace the originalLpnorm, and a new clustering center calculation formula of MSC is therefore derived. The improved MSC clustering algorithm can reduce the computational complexity of MSC fromO(n2mc) toO(nmc) (wherenis the number of data,mis the dimension of data,cis the number of clusters). Experiments results on 5 real data sets including Iris, Breastcancer, Vehicle, User and Wine show that the improved MSC algorithm has competitive clustering precision, but the running time of the improved algorithm is between seventh and one half of the time by original MSC.
clustering algorithm, soft subspace, Minkowski distance, weighted combination
2015-07-23
陕西省自然科学基金资助项目(2014JM8307);陕西省教育厅科学研究计划资助项目(14JK1661)
支晓斌(1976-),男,博士,副教授,从事模式识别研究。E-mail:xbzhi@163.com 高垚琦(1989-),男,硕士研究生,研究方向为信息处理技术及应用。E-mail:826070223@qq.com
10.13682/j.issn.2095-6533.2015.06.012
TP391
A
2095-6533(2015)06-0056-05

