悬索桥对VTS雷达信号的影响分析

母德伟　黄晓冠　韩　述　张　培

(1.重庆交通大学西南水运工程科学研究所　重庆　400016;　2.武汉理工大学　武汉　430063)

悬索桥对VTS雷达信号的影响分析

母德伟1黄晓冠2韩述2张培2

(1.重庆交通大学西南水运工程科学研究所重庆400016;2.武汉理工大学武汉430063)

摘要桥梁的建设将遮挡雷达站微波信号的传输，在大桥附近水域将会形成一定的雷达盲区，导致VTS中心无法掌握该水域的水上交通动态，不能对水上船舶现场进行连续跟踪，也不能对该水域进行有效的监控与指挥，给船舶通航带来了安全隐患。因此，应了解桥梁建设对VTS雷达站的影响，注意桥区监管设施的改善。文中结合悬索桥特点，应用建立的数学模型计算分析悬索桥对VTS雷达信号遮挡的盲区范围，为船舶监控及桥区通航安全提供技术支撑。

关键词悬索桥VTS雷达盲区

对于VTS雷达的盲区形成问题，许多学者进行了有益的研究[1-3]，但目前国内外尚没有桥区水域桥梁对VTS雷达信号遮挡问题的研究。本文以悬索桥为例，分析桥梁与VTS雷达站之间的位置关系，推导出VTS雷达信号盲区的范围，这有助于提高该桥区水域的监管、指挥能力[4-5]，有着较为重要的实际意义。

1桥梁工程对VTS雷达微波的影响

桥梁建设材料主要是混凝土和钢材，这些材料对雷达波束都有很好的反射特性，所以当雷达波束扫过大桥时，会产生大量的回波信息，这些信息将被反射进雷达站的预处理器，需占用较多的

内存容量，预处理器还要花较多的时间来处理这些回波，处理结果还需传送至VTS监控中心，VTS监控中心收到这些回波信息后将在相应的VTS工作站上显示这些回波[6]。因大桥很长又有一定的高度和宽度，所以大桥产生的回波会在VTS工作站的显示屏幕上产生一横跨河道的长条回波带，这样可能会影响驾驶员对大桥回波附近江面物标的观察。

当船舶通过大桥时，由于船舶和大桥离雷达天线间的距离相同，所以船舶和大桥产生的回波出现在同一时刻，使雷达无法从回波中分辩出船舶和大桥，这样雷达就无法直接检测出当时船舶所在的实际位置，而只能通过外推法来推算出船舶所在的位置。由于船舶在过桥时的速度和航向基本不变，所以通过外推法推算出的船舶位置与船舶所在的实际位置误差很小。图1为船舶过桥过程中雷达的回波示意图，回波1是行驶在大桥上游船舶的回波，回波2是大桥和行驶在大桥处船舶的回波，回波3是行驶在大桥下游船舶的回波。

原本两侧雷达都能覆盖的区域，由于大桥对雷达波束的阻挡作用，形成了监控盲区。大桥两侧的雷达都有可能存在跟踪目标丢失的可能，造成监控的不连续，影响对此段水域的船舶航行管理。

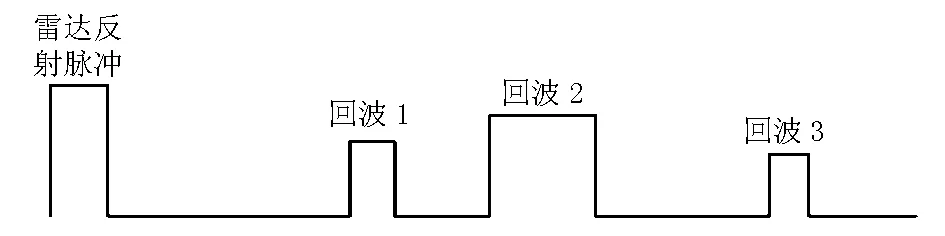
图1　雷达回波示意图

2建桥可能产生的雷达盲区范围计算与分析

以悬索桥为例，图2为悬索桥对VTS雷达微波的遮蔽示意图。图中O标示雷达的最高点，A、D为斜拉桥2主塔的最高点，C点为2主塔拉索的交点，B，E分别为2主桥墩与桥面的交点。

当雷达高度高过拉索的最高点时，则从O点发出的微波经A，B，C，D，E，F和G点，射到水面的点分别为A1，B1，C1,D1,E1,F1和G1点，连接这7点所形成的多边形A1B1C1D1E1F1G1面积，即为悬索桥对雷达的遮蔽面积。

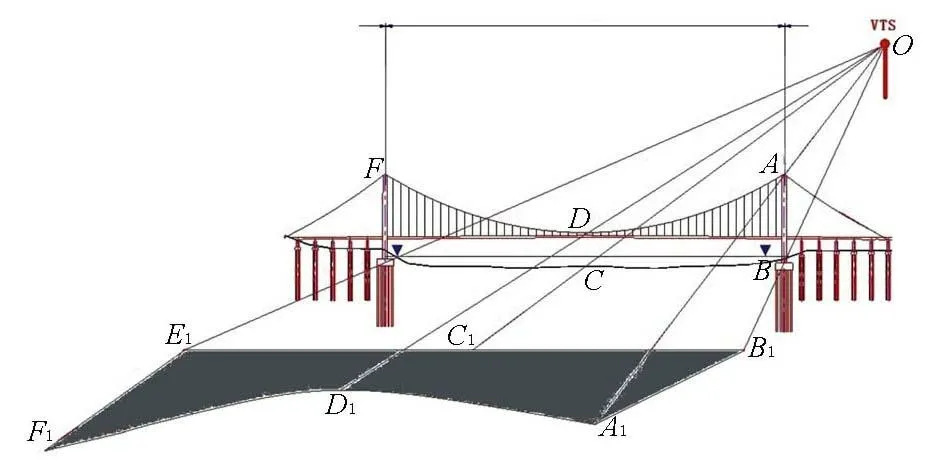
图2　悬索桥对雷达微波遮蔽示意图

要求多边形A1B1C1D1E1F1的面积，首先要分析水面6个点的落点规律。以B点为例，作示意图3：VTS雷达天线的电磁波从O点射出，经过桥面B点，达到水面的B1点。如O点与B点的高程差为d1，O点与水面的高程差为d2。点O1和O分别为点在B和B1高程面内的垂点。假定B与点O1之间水平距离为s1，纵向距离为l1，则：

因为平面O1BB2与平面O2B1B3是平行的，在水面所在高程面内，OO2=d2，得：

从上式知，当B点确定后，B1点距雷达垂线纵向距离l2和水平距离s2只和O点与所求点的高程差有关，因此B，C和E点在水面上形成的落点B1，C1和E1点在一条直线上将A1B1C1D1E1F1的面积适当放大，取四边形A1B1E1F1为遮挡面积，则：

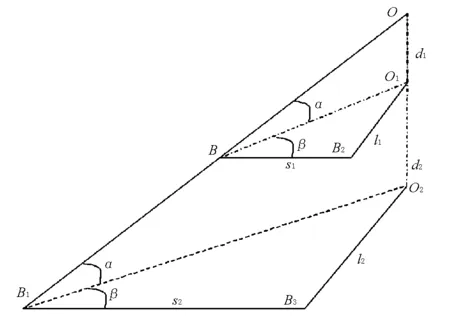
图3　雷达微波经过点与雷达距离分析示意图

3实例分析

现将此模型应用于重庆市轨道交通环线鹅公岩轨道专用桥，计算分析对该桥区范围内VTS雷达的盲区范围。

3.1　重庆市轨道交通环线鹅公岩轨道专用桥概况

重庆市轨道交通环线鹅公岩轨道专用桥是一座横跨长江的特大型桥梁，是重庆市轨道路网规划中环线跨越长江的控制节点工程，位于重庆主城港区的长江三角碛水道，长江上游航道里程约669 km，处在三峡水库变动回水区。

重庆市轨道交通环线鹅公岩轨道专用桥为钢箱梁自锚式悬索桥，桥跨布置2×60 m+210 m+600 m+210 m+3×30 m=1 230 m。塔柱高度160 m，其中下塔柱高90.6 m，上塔柱高69.4 m。见图4。

图4　鹅公岩轨道专用桥桥型(单位：m)

3.2　桥区水域VTS雷达站分布概况

重庆辖区VTS系统，于2010年正式运行，位于长江上游航道里程667 km处的黄沙溪VTS雷达站信号，与重庆市轨道交通环线鹅公岩轨道专用桥桥面的垂直距离约为132 m(见图5)，该雷达站塔高222.6 m。雷达站距离桥的距离为2 km，其中一个主桥墩与雷达站水平距离为200 m。

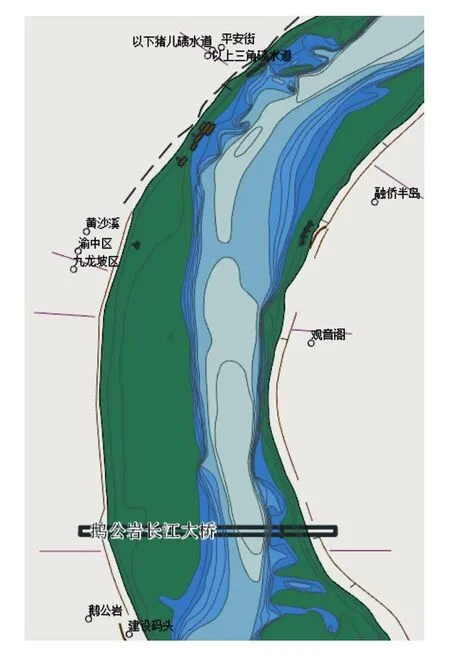
图5　桥梁与VTS雷达站位置关系

3.3　计算分析

运用上述模型进行计算，得到计算结果如下：S遮挡面积=188 438.02 m2。江面宽度约800 m,所以沿岸线盲区长度约为235 m，即在此范围内将会影响VTS中心对过往船舶的监控。

4结语

本文研究了悬索桥对VTS雷达信号的影响，计算分析了VTS雷达监控盲区的区域范围，有助于提高桥区水域的通航安全和桥梁安全系数，并对今后桥梁建设及VTS雷达站选址有着一定的指导意义。但当VTS雷达站的高度小于大桥的主塔高度，但高于桥面高度时，这意味着拟建大桥VTS雷达另一侧的较大一部分水面将无法被雷达监控，其具体情况有待进一步研究。

参考文献

[1]曹德胜,吕靖,艾云飞,等.VTS雷达站选址问题优化模型[J].北京航空航天大学学报,2014(6):727-731.

[2]赵怀森.对雷达盲区的研究[J]. 天津航海,2005(3):3-4.

[3]杜建军.对船舶雷达盲区测定的探讨[J]. 航海,2014(3):56-57.

[4]史云剑.雷达盲区对VTS雷达站选址的影响[C].中国航海学会内河海事专业委员会.2005年度海事管理学术交流会优秀论文集，中国航海学会内河海事专业委员会,2005:4.

[5]吴晓红.雷达盲区和阴影扇形区浅析[J].中国水运,2014,(5):3.

[6]王惠娟.雷达信号识别综合可信度确定的新算法[C].中国指挥与控制学会.2014第二届中国指挥控制大会论文集：上.中国指挥与控制学会,2014：608-611.

Impact of the Suspension Bridge on VTS Radar

MuDewei1，HuangXiaoguan2，HanShu2，ZhangPei2

(1.Scientific Research Institute Chongqing Jiaotong University

Southwest of Port and Waterway Engineering, Chongqing 400016, China;

2.School of Navigation, Wuhan University of Technology, Wuhan 430063, China)

Abstract：The bridge will block the transmission of the microwave signal which comes from the radar station, the formation of certain radar near the bridge will be unable to be grasped by the VTS center, and VTS center cannot continuously track ships on the water scene or monitor ships effectively, which bring safe trouble to ships. Therefore, the impact of bridge construction on VTS radar station and the facility improvement of bridge district supervision should be understood. Combining with the characteristics of suspension bridge and the created mathematical model, the blind area of VTS radar signal being sheltered by suspension bridge is calculated and analyzed. It will provide the technical support for the navigation safety and the ship monitoring.

Key words:suspension bridge; VTS radar; blind area

收稿日期：2015-03-23

DOI 10.3963/j.issn.1671-7570.2015.03.057