某无背索斜塔斜拉人行天桥斜塔截面影响分析

邓世超，徐　懿，龙　云

(贵州智华工程建设有限责任公司)



某无背索斜塔斜拉人行天桥斜塔截面影响分析

邓世超，徐懿，龙云

(贵州智华工程建设有限责任公司)

摘要：介绍了某无背索斜塔斜拉人行天桥斜塔截面影响分析。

关键词：索斜塔；斜拉人行天桥；斜塔；截面；影响分析

1项目概况

本项目为一跨30m无背索斜塔斜拉人行天桥，桥宽4m。桩基、桥墩、承台及斜塔均采用混凝土现浇，主梁采用H型钢与钢板焊接组合钢箱梁，共分10个节段，每节段长3m。通过工厂预制完成后，运至现场拼接成主梁，然后挂索，一次张拉至成桥索力。

2建模分析

对于本桥，难点在于求出每根索的索力，在满足主梁的设计线形及内力的前提下，要使每根索索力较均匀合理。本文采用Midas/Civil建立有限元模型，通过采用未知荷载系数法求解斜拉索索力，可以得到每根拉索索力。

本文重点分析不同截面形式的斜塔(面积相同)对桥梁受力的影响，从而找出较合理截面形式。

对于斜拉桥，关键是要求得适当的索力使成桥后主梁达到设计要求的线形，主塔变形较小。对于主梁有两个重点控制目标：(1)主梁内力较小，应力满足规范要求；(2)位移较小，达到设计线形要求。对于位移，可以通过预拱度加以控制。核心的问题是要控制主梁内力，使主梁无论在施工或成桥状态均满足要求。

3计算结果

现对每个梁段设定目标函数，使主梁弯矩控制在一定的范围(-1 000～1 000kN·m)，从而求得每根拉索索力。各模型下索力比较(S1～S7为内侧至外侧拉索)如下：

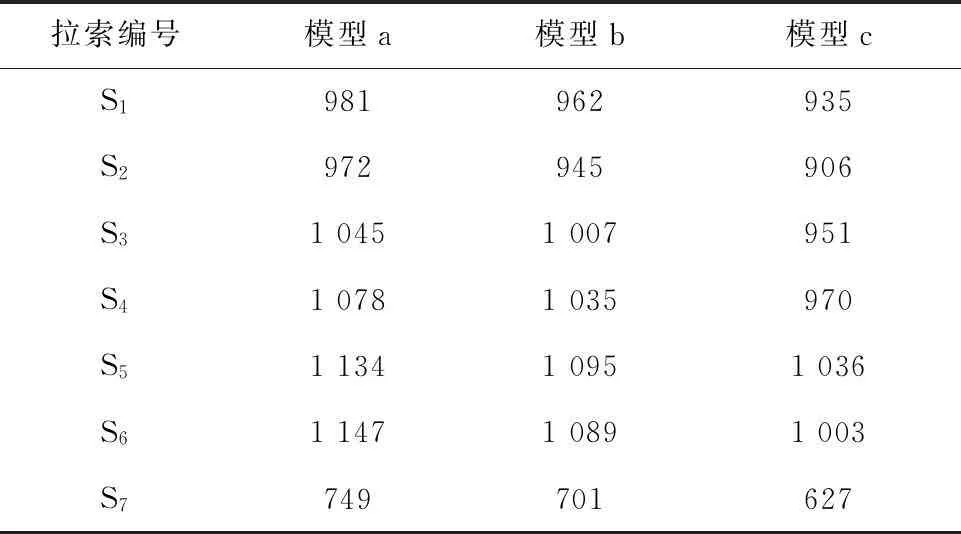
表1　拉索索力　单位：kN

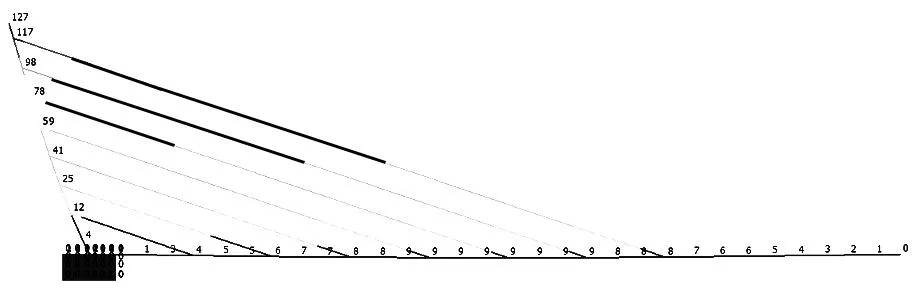
图1　模型a斜塔及主梁位移值(单位：mm)

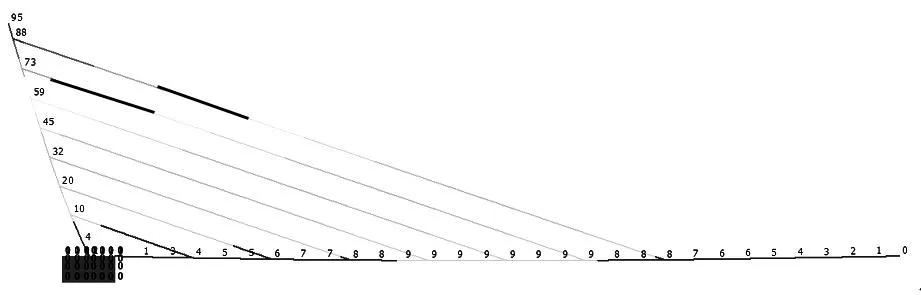
图2　模型b斜塔及主梁位移值(单位：mm)

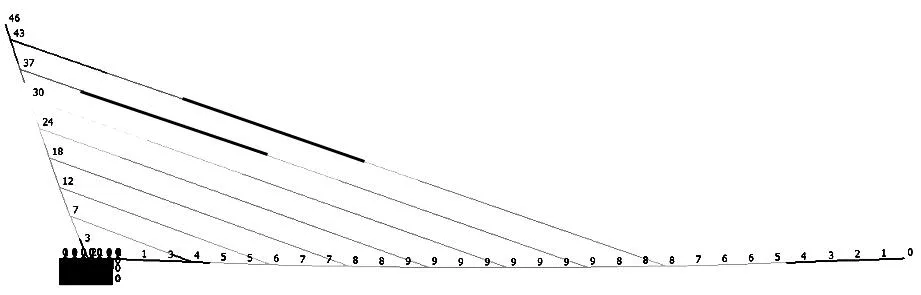
图3　模型c斜塔及主梁位移值(单位：mm)

表2　位移 　单位：mm

通过3个模型对比可知，模型c中斜塔位移最小，模型a最大，模型b居中。

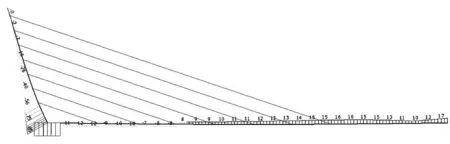
图4　模型a斜塔及主梁应力值(单位：MPa)

图5　模型b斜塔及主梁应力值(单位：MPa)

表3　应力 　单位：MPa

图6　模型c斜塔及主梁应力值(单位：MPa)

负值为压应力，正值为拉应力。通过对比可得模型c中斜塔压应力最小，模型a最大，模型b居中；主梁在3个模型中应力差别较小。

4结论

通过计算模型分析了3种相同截面面积，不同截面形式的斜塔(其余构造均相同)，对拉索索力、斜塔应力、主梁应力所造成的不同影响，从而得出以下结论：

(1)3个模型中主梁应力相差很小，这跟本文把它设为控制目标，从而求得斜拉索索力是对应得起来的。

(2)斜塔底部压应力偏大，实际工程项目中，应增加塔底截面积，降低压应力。

(3)斜塔顶部挠度偏大，应采取措施减小斜塔的位移变形。

(4)3种斜塔截面积均相等，造成3个模型中拉索索力出现较大差别的重要原因在于，斜塔顺桥向抗弯惯矩的差别(模型a～c抗弯惯矩I分别为0.120m4，0.173m4，0.525m4)。

综合以上所述，从拉索受力的均匀性、斜塔位移及应力较小的角度出发，应选择模型c中斜塔截面形式，即工字型截面较为合理。但是从空间布局上看，工字型斜塔截面应尽量优化，使视觉上更轻盈、优美。

参考文献：

[1]邵旭东，程翔云，李立峰.桥梁设计与计算[M].北京：人民交通出版社，2008.

[2]刘士林，王以舜.斜拉桥设计[M].北京：人民交通出版社，2008.

作者简介：邓世超(1980-)，男，工程师。

收稿日期：2015-02-27

中图分类号：U442

文献标识码：C

文章编号：1008-3383(2015)08-0123-02