一道高考题的两种特殊解法

张延德

(贵州省铜仁市第一中学，贵州　铜仁　554300)

一道高考题的两种特殊解法

张延德

(贵州省铜仁市第一中学，贵州铜仁554300)

摘要：斜面上物理受力问题的常规解法是选取水平和竖直方向为x坐标系和y坐标系，需要分解力和加速度，计算过程将较为繁琐.笔者以一道高考选择题为例，运用另类分解法和特殊值法巧解，避免了常规方法的繁琐计算.

关键词：物理高考题；加速度分解；特殊值法

1原题呈现

图1

2013年高考安徽理综第14题如下：如图1所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行.在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，小球受到细线的拉力T和斜面的支持力为FN分别为().

A.T=m(gsinθ+acosθ)，FN=m(gcosθ-asinθ)

B.T=m(gsinθ+acosθ)，FN=m(gsinθ-acosθ)

C.T=m(acosθ-gsinθ)，FN=m(gcosθ+asinθ)

D.T=m(asinθ-gcosθ)，FN=m(gsinθ+acosθ)

本题的常规解法是建立水平和竖直方向的直角坐标系，沿两轴方向分解小球的支持力和拉力，再列式求解，计算过程将较为繁琐.本文将运用两种特别的解法进行解答，使问题的解答变得极为简单快捷.

2方法一：分解加速度

小球受如图2所示的三个力作用，取平行斜面和垂直斜面方向分别为x轴和y轴，分别沿两坐标方向分解重力和加速度.重力分解为：F1=mgsinθ，F2=mgcosθ.加速度分解为：ax=acosθ，ay=asinθ.分别在两坐标用牛顿第二定律列等式：T-mgsinθ=max，mgcosθ-FN=may，解得：T=mgsinθ+macosθ，FN=mgcosθ-masinθ.故本题正确选项为A.

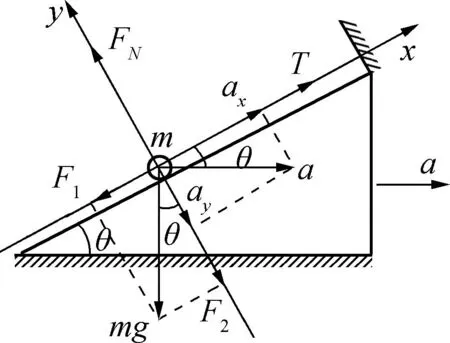
图2

本方法通过分解加速度，使运算过程变得较为简便.

3方法二：特殊值法

图3

设斜面体加速度a=0，则小球和斜面一起向右匀速直线运动，如图3所示，小球所受拉力和支持力的合力F大小一定等于第三个力重力，且方向相反，由几何关系，有：T=mgsinθ，FN=mgcosθ.只有A选项满足假设.

特殊值法在物理选择题中如果使用得当，能帮助我们在极短的时间得出正确答案，一般是所选的物理量存在极值时才能选用该方法.

参考文献：

王跃军.正交分解法常考题型及解析[J].高中数理化，2014，(5、6).