基于POD方法的BBM-Burgers方程向后欧拉有限元降维格式

姜美燕，　朴光日

( 延边大学理学院 数学系， 吉林 延吉 133002 )



基于POD方法的BBM-Burgers方程向后欧拉有限元降维格式

姜美燕，朴光日*

( 延边大学理学院 数学系， 吉林 延吉 133002 )

摘要：利用特征正交分解(proper orthogonal decomposition,POD)方法讨论了BBM-Burgers方程的降维模型.首先，简要介绍了POD方法，并利用此方法把通常的向后欧拉有限元格式简化为一个自由度极少的向后欧拉有限元格式.最后，给出了降维的向后欧拉有限元解的误差估计. 降维模型； 向后欧拉有限元格式； 特征正交分解； 误差分析； BBM-Burgers方程 O241.82

文献标识码：A

0引言

求解复杂的非线性流体方程时，为了得到足够高的精度，任何形式的离散化格式(比如有限元、有限差分、谱元、有限体积等)都需要较多的自由度，从而使得在内存和计算上需要付出很高的代价；因此，在保证其数值解具有足够高精度的前提下，如何简化计算和降低内存要求具有重要意义.降维是解决该问题的有效方法之一，其中特征正交分解(proper orthogonal decomposition,POD)方法是普遍较为熟悉的一种降维方法[1].POD方法具备一种有效逼近大量数据的功能，其实质是在最小二乘意义下可寻找能代表已知数据的一组正交基，是一种求已知数据的最优逼近方法.同时，POD方法可与一些偏微分方程数值解法相结合，将无限维的微分方程降成低维模型，由此能极大地减少计算量和降低内存要求，所以，POD方法已被广泛地应用于很多复杂的系统中[2-12].

当讨论小振幅长波在非线性色散介质中的传播时，为准确反映其真实情况，往往要考虑耗散原理.因为Benjamin-Bona-Mahony-Burgers (BBM-Burgers)方程

ut-uxxt-α uxx+u ux+β ux=0

(1)

包含了非线性色散项和耗散项，因此其被视为一种长波传播的模型方程来加以研究[13].在方程(1)中α>0, β是常数， u=u(x,t)是水平方向上的流体速度.近年来，许多研究者从数学理论和物理意义上研究了BBM-Burgers方程解的性态[13-17],而且还利用有限差分、有限元或区域分解方法讨论了其方程的数值解[18-21].但是，对BBM-Burgers方程的降维模型研究得还较少，如文献[22]虽然给出了基于POD方法的分布反馈控制的简化有限元格式及其科学计算，但并没有讨论通常的有限元解和降维模型解之间的误差分析.本文应用POD方法把BBM-Burgers方程的通常的时间一阶精度向后欧拉有限元格式简化成维数较低的时间一阶精度向后欧拉格式，并类似于文献[23-24]进行了降维的向后欧拉有限元解的误差分析.

本文考虑的BBM-Burgers方程如下：

(2)

1BBM-Burgers方程通常的欧拉有限元格式

对任意的t∈(0,T]， 求u∈X使得满足

(3)

其中(·,·)表示L2-内积.

Xh={Vh∈X∩C0(Ω);Vh|K∈Pm(K),Vh|∂Ω=0,∀K∈ξh}，

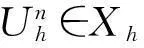
(4)

(5)

(6)

2POD基的生成

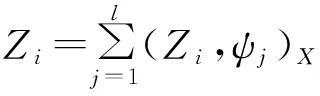
(7)

定义1POD方法是指求标准正交基ψj(j=1,2,…,l)使得对于每个d(1≤d≤l), 元素Zi(1≤i≤N)与式(7)的d项和之间的均方误差最小，即求标准正交基ψj(i=1,2,…,l)使得

(8)

满足

(ψi,ψj)X=δij， 1≤i≤d， 1≤j≤i，

(9)

(10)

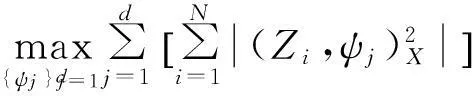
(11)

选择如下形式的一类特殊试验函数ψ:

(12)

(Rψ,ψ)X=∫Ω(Rψ(x)·ψ(x)+Rψ(x)·ψ(x))dx=

∫Ωψ(x)dx=

∫ΩZi(x′)ψ(x′)dx′∫ΩZi(x)ψ(x)

则

(13)

进一步，有(Rφ,ψ)X=(φ,Rψ)X,∀φ,ψ∈X.于是，R是X上的非负定对称算子.由此求式(11)的最大值问题，等价于求式(14)的最大特征值：

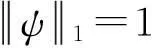
(14)

即

(15)

其中λ与h和k有关(因为ν与h和k有关).将式(12)和G代入到式(15)可得

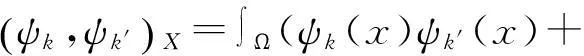
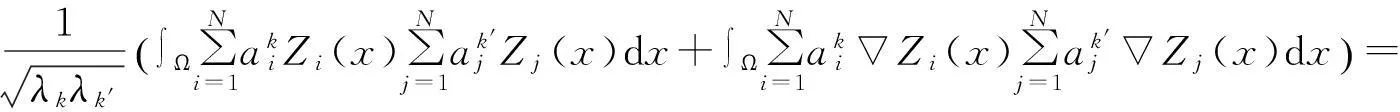
命题1设λ1≥λ2≥…≥λl>0， 为矩阵A的正的特征值，而且υ1,υ2,…,υl是对应的特征向量，则秩d≤l的POD基为

其中(υi)j表示特征向量υi的第j个分量.进一步，有如下的误差公式：

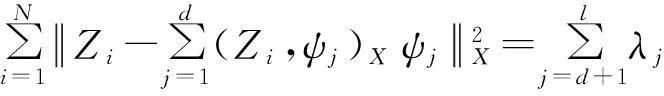
(16)

证明命题的前半部分已经由上述讨论给出.下面仅需证明公式(16).由于ψ1,ψ2,…,ψl满足式(14)，所以从式(13)和(15)可得

(17)

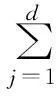
(18)

命题1得证.

令Xd=span{ψ1,ψ2,…,ψd}.定义Ritz投影Ph∶X→Xh(如果Ph是被限制为从Xh到Xd的Ritz投影时记为Pd)， 使得Ph|Xh=Pd∶Xh→Xd和Ph∶XXh→XhXd如下：

(PhU,Vh)X=(U,Vh)+(U,Vh)，∀Vh∈Xh，

(19)

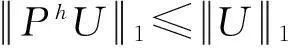
引理1对于每个d(1≤d≤l)， 投影算子Pd满足：

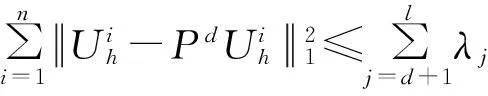
(20)

(21)

证明对于任意的U∈X， 由式(19)得

因此有

(22)

(W,V)X=(U-PhU,V),∀V∈Xh.

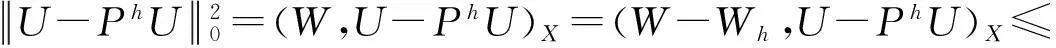
(23)

取Wh=πhW为W在Xh上的差值，则由插值理论[27]和式(23)可得

于是有

(24)

3基于POD方法的简化欧拉有限元格式及其误差估计

利用Xd可以将方程(4)化为如下的基于POD方法的向后欧拉有限元降维格式：

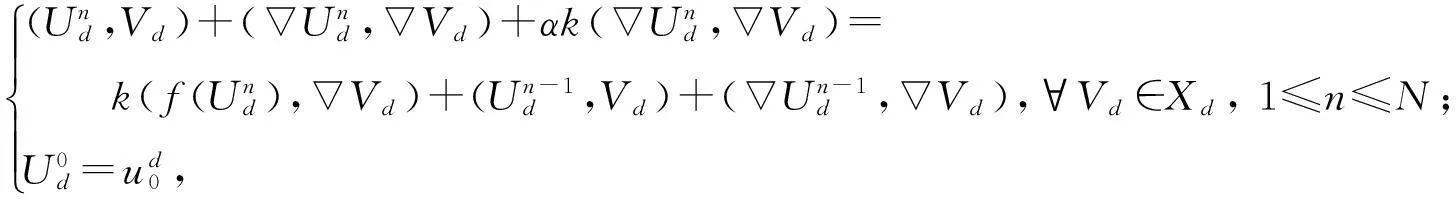
(25)

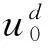
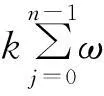
对于BBM-Burgers方程向后欧拉有限元降维格式,式(25)有如下的解的误差估计：

(26)

(27)

其次，证明误差估计式(27).由于Xd⊂Xh， 在式(4)中取Vh=Vd并与式(25)相减可得

(28)

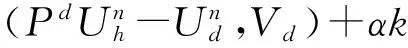
αk(,,

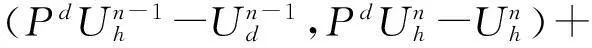
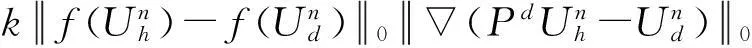
简化后可得

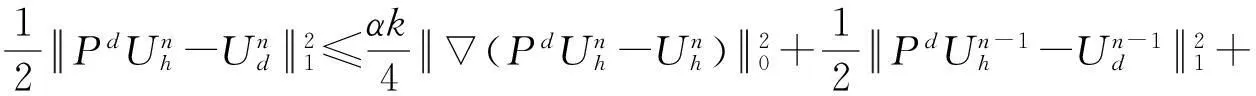
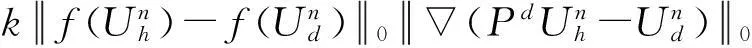
(29)

上式对n从1到J(≤N)累加，即得(为了书写方便用n代替J)

选取充分小的k， 使得当(1-Ck)≥0时，有

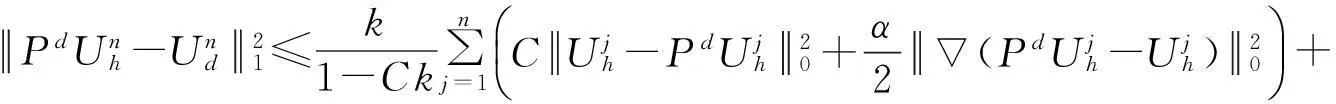
再由引理1和引理2，得

(30)

根据Sobolve嵌入定理、三角不等式、引理1和式(30)可得到式(27),定理2得证.

参考文献：

[1]HolmesP,LumleyJL,BerkoozG.Turbulence,CoherentStructures,DynamicalSystemsandSymmetry[M].Cambridge:CambridgeUnivPress, 1996.

[2]BerkoozG,HolmesP,LumleyJ.Theproperorthogonaldecompositionintheanalysisofturbulentflows[J].AnnRevFluidMech, 1993,25:539-575.

[3]BerkoozG,TitiE.Galerkinprojectionsandtheproperorthogonaldecompositionforequivariantequations[J].PhysLett, 1993,A174:94-102.

[4]BurkardtJ,GunzburgerM,LeeHC.PODandCVT-basedreduced-ordermodelingofNavier-Stokesflows[J].CompMethApplMechEngrg, 2006,196:337-355.

[5]ChristensenE,BronsM,SorensenJ.Evaluationofproperorthogonaldecompositionbaseddecompositiontechniquesappliedtoparameter-dependentnonturbulentflows[J].SIAMJSciComp, 2000,21:1419-1434.

[6]DeaneA,KeverkidisI,KarniadakisG,etal.Low-dimensionalmodelsforcomplexgeometryflows:applicationtogroovedchannelsandcircularcylinders[J].PhysFluidsA, 1991,3:2337-2354.

[7]KunischK,VolkweinS.ControloftheBurgersequationbyareduced-orderapproachusingproperorthogonaldecomposition[J].JOptimTheoryAppl, 1999,102:345-371.

[8]LeeHC,PiaoGR.BoundaryfeedbackcontroloftheBurgersequationsbyareduced-orderapproachusingcentroidalVoronoitessellations[J].JSciComp, 2010,43:369-387.

[9]LyHV,TranHT.Modelingandcontrolofphysicalprocessesusingproperorthogonaldecomposition[J].CompMathAppl, 2001,33:223-236.

[10]ParkH,LeeJ.Solutionofaninverseheattransferproblembymeansofempiricalreductionofmodes[J].ZAngewMathPhys, 2000,51:17-38.

[11]ParkH,LeeW.AnefficientmethodofsolvingtheNavier-Stokesequationsforflowcontrol[J].IntJNumerMechEng, 1998,41:1133-1151.

[12]PiaoGR,LeeHC,LeeJY.DistributedfeedbackcontroloftheBugersequationbyareduced-orderapproachusingweightedcentroidalVoronoitessellation[J].JKSIAM, 2009,13:293-305.

[13]BenjaminTB,BonaJL,MahonyJJ.Modelequationsforlongwavesinnonlineardispersivesystems[J].PhiTransRoySocLondon:SeriesA, 1972,272:47-78.

[14]BonaJL,DougalisVA.Aninitialandboundaryvalueproblemforamodelequationforpropagationoflongwaves[J].JMathAnalAppl, 1980,75:503-522.

[15]MeiM.Large-TimebehaviorofsolutionsforBenjamin-Bona-Mahony-Burgersequations[J].NonlinearAnalysis,1998,33:699-714.

[16]ZhangH,WeiGM,GaoYT.OnthegeneralformoftheBenjamin-Bona-Mahonyequationinfluidmechanics[J].CzechJPhys, 2002,52:344-373.

[17]ChenY,LiB,ZhangH.Exactsolutionsoftwononlinearwaveequationswithsimulationtermsofanyorder[J].CommNonlinearSciNumerSimulation, 2005,10:133-138.

[18]OmraniK,AyadiM.FinitedifferencediscretizationoftheBenjamin-Bona-Mahony-Burgers(BBMB)equation[J].NumerMethPartialDiffEq, 2008,24:239-248.

[19]OmraniK.TheconvergenceofthefullydiscreteGalerkinapproximationsfortheBenjamin-Bona-Mahony(BBM)equation[J].ApplMathComput, 2006,180:614-621.

[20]Al-KhaledK,MomaniS,AlawnehA.ApproximatewavesolutionsforgeneralizedBenjamin-Bona-Mahony-Burgersequations[J].ApplMathComp, 2005,171:281-292.

[21]KadriT,KhiariN,AbidiF,etal.MethodsforthenumericalsolutionoftheBenjamin-Bona-Mahony-Burgersequation[J].NumericalMethodsforPartialDifferentialEquations, 2008,24:1501-1516.

[22]PiaoGR,LeeHC.DistributedfeedbackcontroloftheBenjamin-Bona-Mahony-Burgersequationbyareduced-ordermodel[J].EastAsianJournalAppliedMathematics， 2015,5(1):61-74.

[23]LuoZhendong,ZhouYanjie,YangXiaozhong.AreducedfiniteelementformulationbasedonproperorthogonaldecompositionforBurgerequation[J].ApplNumerMath, 2009,59:1933-1946.

[24]罗振东，陈静，谢正辉，等.抛物型方程基于POD方法的时间二阶精度CN有限元降维格式 [J].中国科学:数学，2011,41(5):447-460.

[25]AdamsRA.SobolevSpace[M].NewYork:AcademicPress, 1975.

[26]ThoméeV.GalerkinFiniteElementMethodsforParabolicProblems[M].Berlin:Springer-Verlag, 1984.

[27]CiarletPG.TheFiniteElementMethodforEllipticProblems[M].Amsterdam:North-Holland, 1978.

[28]AtouaniN,OmraniK.GalerkinfiniteelementmethodfortheRosenau-RLWequation[J].CompuMathAppl, 2013,66:289-303.

A reduced-order backward Eular finite element scheme for the BBM-Burgers equation based on POD

JIANG Meiyan,PIAO Guangri*

(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)

Abstract：In this paper, we study reduced-order modeling for the BBM-Burgers equation by using proper orthogonal decomposition (POD) method. First of all, brief review of the POD method are provided; secondly, the POD method is applied to a usual backward Euler finite element (BEFE) scheme such that it is reduced into a BEFE scheme with fewer degrees of freedom, and the errors of reduced-order BEFE solution are analyzed.

Keywords：reduced-order modeling； backward Euler finite element method； proper orthogonal decomposition； error analysis； BBM-Burgers equation

文章编号：1004-4353(2015)04-0267-08

*通信作者：朴光日(1968—)，男，博士，副教授，研究方向为数值计算.

收稿日期：2015-11-03