锈蚀后钢材弹性模量与屈服强度的计算模型

徐善华，任松波

(西安建筑科技大学土木工程学院， 西安 710055)



锈蚀后钢材弹性模量与屈服强度的计算模型

徐善华，任松波

(西安建筑科技大学土木工程学院， 西安 710055)

摘要：根据点蚀坑的特点，将锈蚀钢材表面点蚀坑简化为半椭球形，引入锈蚀损失率作为锈蚀损伤参量，并利用细观损伤力学和自洽方法建立锈蚀后钢材的锈蚀损伤弹性理论模型；再对Q235钢进行室内盐雾加速试验和单向拉伸试验，得到不同锈蚀时间试样的锈蚀损失率、弹性模量和屈服强度，并将单向拉伸试验结果与模型计算结果进行了对比验证。结果表明：使锈蚀速率临界点提前可显著降低锈蚀对钢结构材料造成的损伤;模型计算值与试验值吻合较好，验证了所建立计算模型的可行性和正确性。

关键词：点蚀坑；细化损伤力学；钢；弹性性能

0引言

建筑结构用钢作为主要承重构件不可避免地受到环境因素作用而发生锈蚀，导致其力学性能降低。锈蚀造成的钢材性能下降是一个微观损伤的过程，应该从微观角度去分析。

近年来，众多学者已经开始从微观角度对锈蚀钢材进行研究，Gurson[1]通过对含有锈蚀孔试样的试验研究，提出了适用于延性多孔材料的细观损伤本构模型，该模型可以描述由初始微孔洞增长、成核和最后聚合而导致的宏观材料受力破坏现象;Tvergaard[2-3]和Needleman[4-5]通过引入由试验推导得到的附加拟合参数qi分别对Gurson模型进行了修正，并用试验验证了修正模型能够很好地反映表面微孔材料宏观塑性的流动影响;Laycock[6]通过分析大量不同锈蚀时间钢材表面的锈蚀坑信息，建立了一个基于广义极值分布的四参数锈蚀形貌模型，利用该模型可对特定条件下钢材表面锈蚀坑数量、大小及其分布方差等数理参数进行预测;陈小平等[7]通过扫描电镜等方法对腐蚀钢的锈层形貌和结构进行分析，发现锈蚀初期耐候钢和碳钢锈层组织的主要成分分别为α-FeOOH和Fe2O3，同时还发现枝晶尺寸纤细的α-FeOOH对未锈蚀基体具有保护作用，而枝晶粗大的Fe2O3疏松多孔，对基体不具备保护性;Fuente等[8]采用XRD和SEM / EDS对大量既有自然锈蚀试样的微观结构进行观察，归纳了锈蚀各阶段的产物主要有: γ-FeOOH、α-FeOOH、β-FeOOH、Fe3O4/γ-Fe2O3、Fe5HO8·4H2O和α-Fe2O3，且农村地区的锈蚀产物γ-FeOOH含量可达60%以上，工业区及城市次之,同时发现α-FeOOH对锈蚀发展有一定的抑制作用。

这些研究大多从各自领域对材料表面锈蚀特征和微孔效应进行分析，而锈蚀材料的性能改变需要从锈蚀损伤方面来研究。为此，作者将细观力学的概念引入到了对锈蚀钢弹性性能的预测中，建立了表面锈蚀坑损伤钢材弹性性能的计算模型；通过对Q235钢进行室内盐雾加速连续腐蚀试验测定锈蚀损失率，通过建立的腐蚀损伤模型计算锈蚀试样的弹性模量；利用静力拉伸试验对锈蚀试样的弹性模量及屈服强度进行测试，然后将试验结果与计算结果进行对比分析，以验证所建立的计算模型的可行性和正确性，为钢结构材料力学性能的预测提供参考。

1锈蚀损伤模型

点蚀又称孔蚀，是钢铁表面电化学反应后形成的[9]。通常，钢铁在一定环境条件下，表面会发生一系列电化学反应，形成大量肉眼可见的微孔。这些微孔体积不断增长[10]，从金属表面逐渐深入到金属内部，形成与外界连通的单独或联合点蚀群，进而引起金属性能降低。Mattsson[11]通过大量试验发现点蚀坑的深度与锈蚀时间的立方根成正比：

(1)

式中：a为点蚀坑深度；C为环境参数；t为锈蚀时间。

由于金属点蚀坑的扩展是由表面电化学反应引起的，因此点蚀坑的形状可以近似认为是半椭球形的[12]，结合电化学反应和法拉第定律，将点蚀坑深度的增长速度表达为下式:

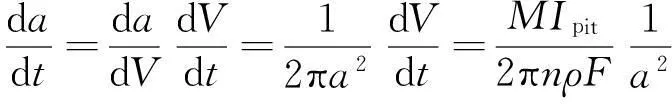
(2)

式中：V为点蚀坑体积；M为金属相对原子质量；n为腐蚀过程中金属原子价；F为法拉第常数；Ipit为点蚀坑腐蚀电流强度；ρ为金属密度。

将式(2)整理，两边积分得：

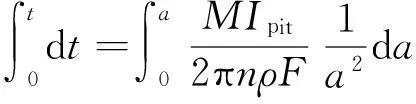
(3)

整理式(3)，可得半椭球点蚀坑深度与锈蚀时间的关系：

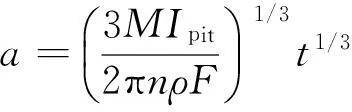
(4)

根据文献[11]，金属表面点蚀坑为电化学类锈蚀产生的半椭球形微孔洞损伤，存在于锈蚀金属表面的大量孔洞多以孔隙率表示。在细化损伤力学中，孔隙率被定义为材料中所含孔隙体积与材料体积之比，可作为材料损伤的评价因子。假设材料在未锈蚀前不含孔隙，且锈蚀前后的密度不变，则可以得到孔隙率与锈蚀损失率之间的关系:

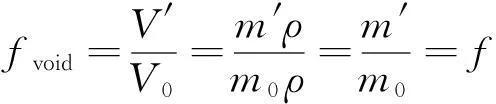
(5)

式中：fvoid为孔隙率；V′为微孔洞体积；V0为未锈蚀前材料体积；m′为锈蚀造成的材料质量损失；m0为未锈蚀前材料质量；ρ为材料密度；f为锈蚀损失率，即为锈蚀材料除锈后剩余质量与未锈蚀前质量之比。

由此可见，当微孔表示锈蚀损伤时，微孔孔隙率则可由锈蚀损失率代替。因此，作者认为,锈蚀钢材的弹性性能细观劣化程度可由锈蚀损失率来表征。

另外，分布于锈蚀界面的大量锈蚀微孔彼此相互作用，形成点蚀群，它们对材料的损伤作用异于单孔损伤。因此作者采用量子力学自洽方法，将每个微孔损伤置于具有自洽等效模量的材料上，充分考虑微孔损伤之间的相互影响[12]。这个方法的要点在于将一种介质受到熵域范围内介质的作用以平均场当量来代替，并将多体之间的相互作用转换为单体准粒子系统，在一级近似下得到正确结果[13]。

因着海兰抱病，今日并未去大殿行哭礼，青樱见她立在门外，便道：“这样夜了怎么还来？着了风寒更不好了，快进来罢。”

Budiansky[14]提出材料等效体积模量与各相体积模量之间存在如下关系：

(6)

(7)

式中：K为表面含锈坑材料的等效体积模量；K0为材料初始体积模量；Ki为材料中各相的体积模量；Ci为常数； G0为材料初始剪切模量；N为损伤点个数。

在静力载荷作用下，沿载荷方向材料的等效体积弹性模量由式(6)推导可得：

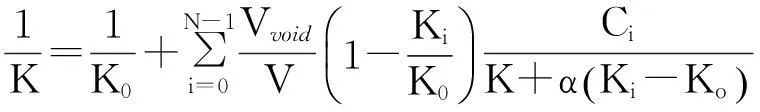
(8)

将式(5)，(6)，(8)进行整理，可得含有表面锈坑损伤的材料等效体积模量：

(9)

由材料力学[15]可知:

(10)

式中：E为表面含锈坑材料的等效弹性模量；ν为泊松比。

将式(9)，(10)整理得到含有表面锈坑损伤的材料等效体积模量：

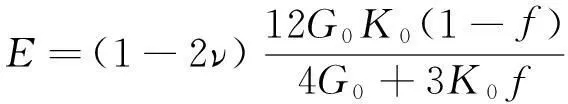
(11)

将未锈蚀Q235钢的物理参数(ν为0.25，K0为120 GPa，G0为72 GPa)代入式(11)，得到表面含锈蚀坑的Q235钢等效弹性模量表达式：

(12)

利用Tvergaard模型[2]对含有表面锈蚀坑群损伤的钢材屈服强度进行评估，该模型利用幂函数基体硬化关系对Gurson模型[1]进行了修正，充分考虑了锈蚀钢材表面锈蚀坑群之间相互作用的屈服条件：

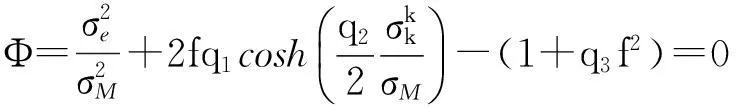
(13)

2试样制备与试验方法

为验证模型计算结果的可行性和正确性，采用Q235钢进行室内盐雾加速腐蚀试验，其化学成分见表1。所加工试样的尺寸为280 mm×50 mm×8 mm。腐蚀试验后，对不同锈蚀时间的试样进行静力拉伸试验。

表1　Q235钢的化学成分(质量分数)

腐蚀试验前，对试样进行分组编号，并分别测其质量(m0)。室内加速腐蚀试验采用YMX/Q-020型盐雾箱，腐蚀溶液为5%(质量分数)氯化钠溶液，溶剂为蒸馏水。试验时，将20组试样同批置于盐雾箱内，设置箱内温度为35 ℃，饱和器温度为37 ℃，相对湿度大于95%，进气压力0.2～0.3 MPa，压缩空气压力0.07～0.17 MPa，喷雾量80 cm3·h-1，pH为6.5～7.2。采用间隙喷雾，周期为12 h，单周期内连续喷雾6 h，停喷6 h，停喷不加热，箱体密封。锈蚀时间分别为14，28，42，56，70，84，98，118，138，178 d。

室内盐雾加速腐蚀试验完成后，将试样从盐雾箱内取出并进行机械除锈(勿损基质)，然后浸入12%(体积分数)的稀盐酸溶液中浸泡20～30 min，用钢刷清洗表面腐蚀产物，再用氢氧化钠溶液中和，轻轻敲击并反复清洗至锈蚀孔洞内锈蚀产物被彻底清除，最后用清水对试样进行冲洗，置于干燥箱内烘干，测其除锈后残余质量(m′)，根据式(5)计算锈蚀损失率(f)。

锈蚀试样按照GB/T 228.1-2010的规定加工成静力拉伸试样，并确保不破坏试样的原始腐蚀形貌，不产生残余应力，没有对表面造成损伤和变形。拉伸试样的侧面采取抛光方式处理，表面粗糙度小于0.01 mm，加持区和试验工作区采用圆弧过渡，试样尺寸见图1。

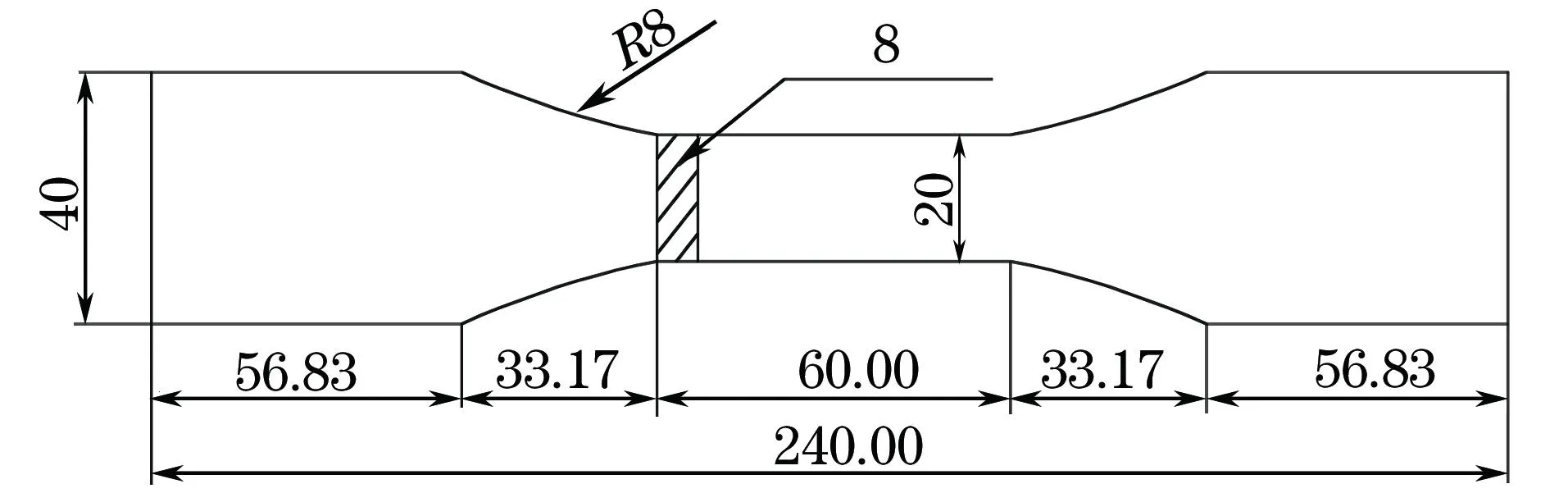
图1　静力拉伸试样尺寸Fig.1　Shape and size of tensile specimen

静力拉伸试验在CSS-WAW300DL型电液伺服万能试验机上完成。试验开始前先预加载荷并观察仪表是否正常，若不正常应该及时进行调整，待检查无问题后，卸载到零，再开始正式加载。试验过程中数据采集系统自动采集数据，将引伸计夹在试样中间部位，其标距为50 mm，当载荷有下降趋势时，为防止引伸计被拉坏，故将其取下，待试样被拉断后，用游标卡尺在其标距范围内测量其延伸量，精确到0.02 mm，并计算其极限伸长率。锈蚀试样拉断后形态见图2。

图2　锈蚀试样拉断后形态Fig.2　Fracture shapes of tensile corrosion specimens

3试验结果与讨论

由表2可知，随着锈蚀天数的增加，试样的锈蚀损失率增加，力学性能降低。当锈蚀时间为178 d时，锈蚀损失率最大,可达11%左右，弹性模量最大下降13.9%，屈服强度最大下降14.5%；当锈蚀时间超过56 d，试样的弹性模量和屈服强度下降速率均明显放缓。主要原因分析如下：

(1) 随着锈蚀时间的增加，试样表面锈蚀坑逐渐增大变深，表面损伤加重，点蚀坑之间相互影响更加显著；同时，锈蚀坑内的锈蚀产物体积增大，膨胀应力促使试样的损伤积累更甚，因此力学性能降低。

(2) 参考文献[7-8]，在盐雾环境中，锈蚀初期锈蚀产物主要成分为Fe2O3，约占80%以上，该物质可大大降低被腐蚀钢材的力学性能；而在锈蚀中期(相当于56 d锈蚀期)，锈蚀产物中会逐渐出现α-FeOOH，该物质枝晶纤细，晶体形貌呈致密团状，力学性能优良，对锈蚀损伤具有一定弥补效果，故而会出现力学性能劣化速率临界区。但由于锈蚀产物组织中较稳定的羟基氧化铁含量较少，因此在理论上认为α-FeOOH对计算模型的影响可忽略不计。

根据表2中锈蚀损失率和锈蚀时间的试验数据，采用最小二乘法对锈蚀损失率进行线性回归分析得到Q235钢的f-t关系曲线(R2=0.96)。由图3可知，锈蚀损失率随锈蚀时间的延长而增加，且增加速率逐渐减小。由于钢材在锈蚀过程中，当锈蚀产物积累到一定量时可对锈蚀的继续扩展起阻碍作用[7]，因此随着锈蚀时间的延长，锈蚀损失率的增长幅度逐渐减缓，即锈蚀损失速率随锈蚀时间的增加而降低。此外，由于锈蚀产物对锈蚀发展的抑制作用，锈蚀损失速率在整个锈蚀时间内存在一个分界点，该分界点可将锈蚀损失速率在整个材料锈蚀过程中分为两部分：前一部分为锈蚀产物积累期，由于锈蚀产物的大量累积，材料锈蚀损失速率被抑制，衰减显著；后一部分随着锈蚀产物的积累，材料锈蚀损失速率将逐渐趋于稳定。将该分界点称为锈蚀损失速率临界点。由图3可知，Q235钢的锈蚀损失速率临界点大致位于56 d。基于此，提前锈蚀损失速率临界点的方法可有效减缓锈蚀损伤对钢材造成的损伤，例如涂刷类α-FeOOH物质层。

将表2中锈蚀损失率分别代入式(12)和(13)，计算得到锈蚀试样弹性模量和屈服强度随锈蚀损失率变化的曲线，见图4。由图4可知，Q235钢的弹性模量与屈服强度试验值虽分散于模型计算结果两侧，但均随锈蚀损失率的增加而减小。该离散结果可如下分析：由于在损伤模型推导过程中，将点蚀坑

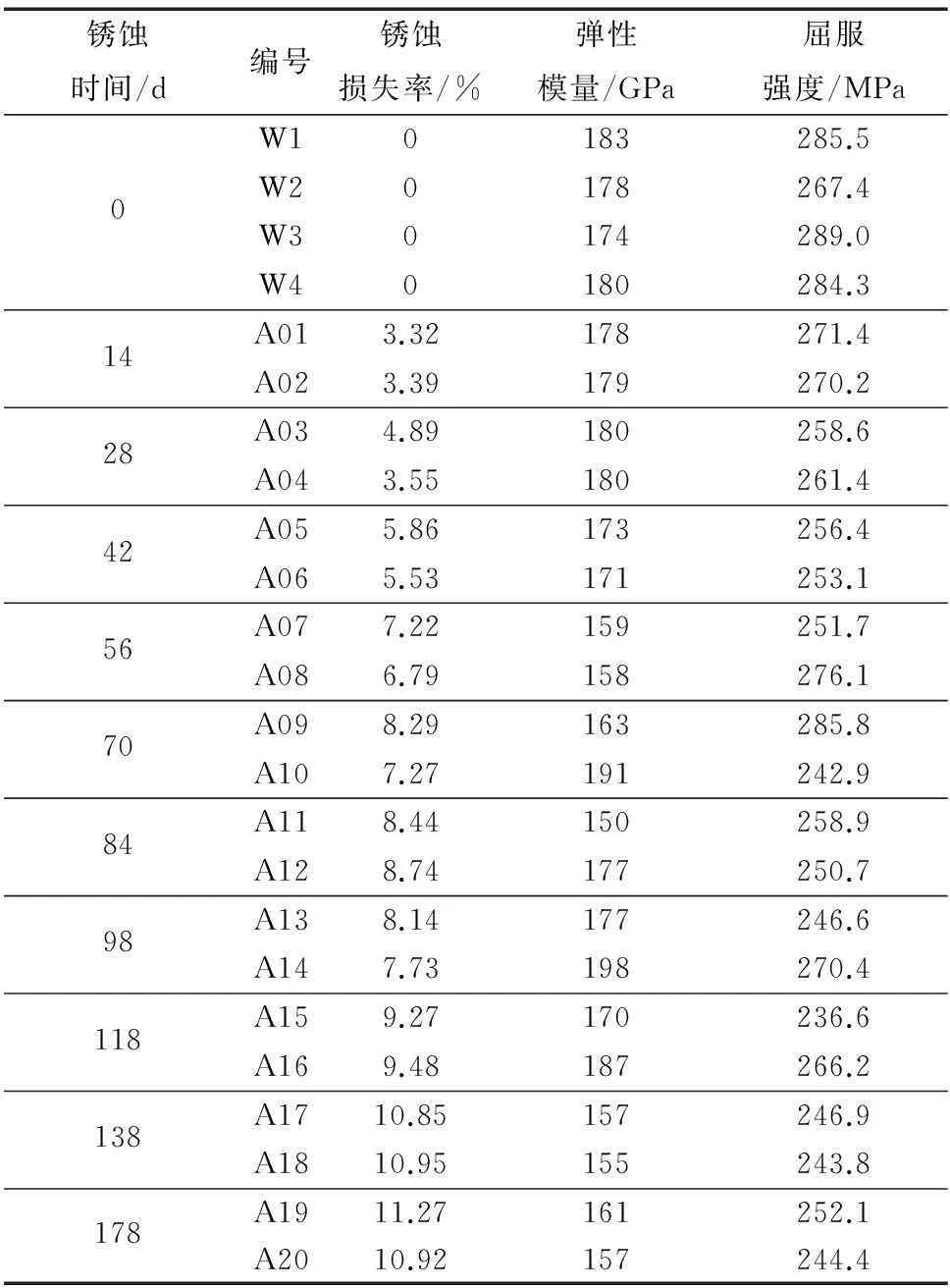
表2　室内盐雾加速腐蚀试验和拉伸试验结果

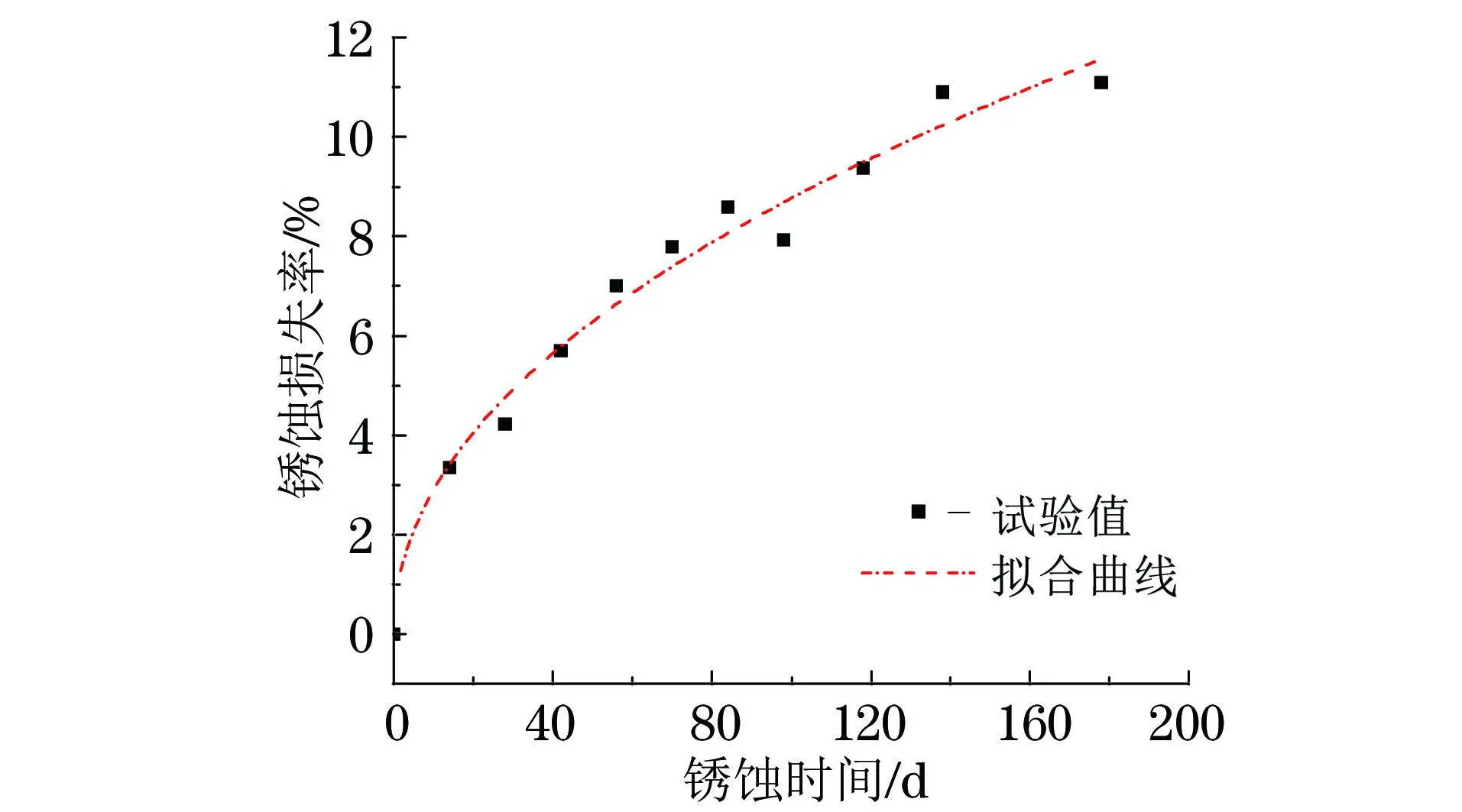
图3　锈蚀Q235钢的f-t关系曲线Fig.3　Relationship between corrosion time and corrosionloss rate of corrosion Q235 steel

形状等效为半椭球形，该等效在一定程度上可降低锈蚀试样表面的应力集中效应，因此模型所计算的弹性模量和屈服强度与其试验值存在一定偏差，相对偏差分别为9.71%和4.33%。锈蚀损伤使得金属表面晶格产生畸变，势能增加，体系混乱度增大，自由能升高，稳定性降低，低应力条件下可发生高应变，加之损伤模型等效方法对试样表面应力集中效应的降低作用，最终导致锈蚀试样弹性模量的计算值较其试验值低。屈服强度为金属抵抗微量塑性变形对应的应力，而点蚀坑等效简化对锈蚀试样塑性变形的产生及发展无显著影响，故锈蚀试样屈服强度的计算值与其试验值偏差甚微。

此外，由于试验过程中存在仪器误差和测量误差，锈蚀试样的弹性模量和屈服强度试验值均随锈蚀损失率的增加呈离散型下降趋势，且波动较为明显。

综上所述，计算结果和试验结果具有很好的一致性，这也说明锈蚀钢弹性性能预测模型的准确性。

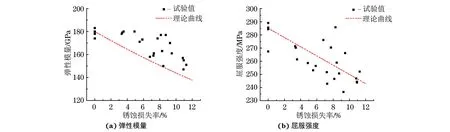
图4　不同锈蚀损失率Q235钢的弹性模量和屈服强度Fig.4　Elastic modulus(a) and yield stress(b) of Q235 steel at different corrosion loss rates

4结论

(1) 按照锈蚀坑扩展规律，引入锈蚀损失率来表征钢材锈蚀损伤程度，将其作为锈蚀损伤参数；从锈蚀损伤机理出发，建立锈蚀损伤钢材弹性性能理论模型，该模型能够很好地反映锈蚀损失率对钢材弹性性能的影响。

(2) 随着锈蚀天数的增加，锈蚀损失率增大，钢材弹性模量和屈服强度下降；锈蚀损失率增长速率和力学性能下降速率逐渐减弱；当锈蚀时间超过56 d，锈蚀损失率增长速率和力学性能下降速率明显低于锈蚀前期的，因此提前锈蚀损失速率临界点可显著降低锈蚀对钢材造成的损伤;与此同时，该锈蚀损失速率临界区的存在对计算模型的量化评估影响微弱，可忽略不计。

(3) 锈蚀Q235钢的弹性模量与屈服强度的计算值与试验值相对误差分别为9.71%和4.33%，该锈蚀损伤模型可用于量化预测不同锈蚀时间下钢材的弹性模量和屈服强度。

参考文献:

[1]GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I. Yield criteria and flow rules for porous ductile media[J]. Journal of Engineering and Technology, 1977, 99(1):2-5.

[2]TVERGAARD V. Influence of voids on shear band instabilities under plane strain conditions[J]. International Journal of Fracture, 1981, 17(4): 389-407.

[3]TVERGAARD V. On localization in ductile materials containing spherical voids[J].International Journal of Fracture,1982,18(4): 237-252.

[4]NEEDLEMAN A, TVERGAARD V. An analysis of ductile rupture in notched bars[J]. Journal of the Mechanics and Physics of Solids, 1984, 32(6): 461-490.

[5]TVERGAARD V, NEEDLEMAN A. Analysis of the cup-cone fracture in a round tensile bar[J]. Acta Metallurgica, 1984, 32(1): 157-169.

[6]LAYCOCK P J, COTTIS R A, SCARF P A. Extrapolation of extreme pit depths in space and time[J]. Journal of the Electrochemical Society, 1990, 137(1): 64-69.

[7]陈小平, 王向东, 刘清友, 等. 耐候锈层的耐腐蚀机理研究[J]. 腐蚀与防护, 2009, 30(4): 241-243.

[9]曹楚南.中国材料的自然环境腐蚀[M]. 北京：化学工业出版社，2005.

[10]SHI P, MAHADEVAN S. Damage tolerance approach for probabilistic pitting corrosion fatigue life prediction[J]. Engineering Fracture Mechanics, 2001, 68(13): 1493-1507.

[11]MATTSSON E. Basic corrosion technology for scientists and engineers[M]. Chichester: Ellis Horwood, 1989.

[12]ILEVINE I N. Quantum Chemistry[M]. Upper Saddle River, NJ: Pearson Prentice Hall, 2009.

[13]DIRAC P A M. The Principles of Quantum Mechanics[M]. London: Oxford University Press, 1982:2-2.

[14]BUDIANSKY B.On the elastic moduli of some heterogeneous material[J]. J Mech Phys Solids, 1965,13(4):223-227.

[15]孙训方.材料力学[M].北京：北京教育出版社，2002.

The Calculation Model of Elastic Modulus and Yield Strength

for Corroded Steel

XU Shan-hua，REN Song-bo

(School of Civil Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China)

Abstract:The corrosion pit on the steel surface was considered as the semi-ellipsoid based on its characteristics, and the corrosion loss rate was introduced as a damage parameter, then the elastic model of the steel corrosion damage was established by using the damage micromechanics and self-consistent method. The corrosion loss rate, elastic modulus and yield strength of Q235 steel for various corrosion periods was obtained by the indoor salt spray accelerated test and uniaxial tensile test and compared with the simulation values from the elastic model. The results show that early critical point of corrosion rate reduced the damage of corrosion on structural steel significantly; the experiment value was consistent with the theoretical calculation value, indicating the excellent feasibility and accuracy of the established theoretical model.

Key words:corrosion pit; damage micromechanics; steel; elastic property

中图分类号：TU501;TG171

文献标志码：A

文章编号：1000-3738(2015)10-0074-05

作者简介：徐善华(1963-)，男，江苏南通人，教授，博士。

基金项目：国家自然科学基金资助项目(50778151,51078307)；陕西省教育厅科研计划资助项目(07JK300)

收稿日期:2014-09-05；

修订日期:2015-07-21

DOI:10.11973/jxgccl201510017