基于马达代数的交会对接相对位姿测量算法

陈伟 陈志明 王惠南

(南京航空航天大学航天学院，南京 210016)



基于马达代数的交会对接相对位姿测量算法

陈伟 陈志明 王惠南

(南京航空航天大学航天学院，南京 210016)

精确测量追踪航天器与目标航天器之间的相对位姿关系是成功完成航天器交会对接任务的关键。传统的位姿测量算法将旋转和平移分而视之，破坏了三维运动的统一性，同时增加了算法的复杂性和计算难度。针对这个问题，采用双目视觉测量方法，在马达代数框架内，以两个特征光点确定的特征直线为变换基元，统一描述并设计算法测量追踪与目标航天器之间的位姿关系，最终将两航天器之间的相对位姿解算问题简化为求解两个线性方程组。该方法在计算形式上更为简洁，且测量受特征光点的安装位置限制较小。仿真结果表明，算法具有较高的精度和稳定性，可以满足航天器交会对接任务的要求。

马达代数；交会对接；相对位姿；双目视觉；航天器

1 引言

在航天器交会对接的最终逼近段，追踪航天器必须自主精确测定与目标航天器的相对姿态和相对位移，并通过控制使其相对状态满足最终逼近段准直线运动、逼近速度、安全性及软对接等多项技术要求[1-2]。目前普遍的测量方法是在目标航天器上设置光学特征点，利用特征点在CCD相机视觉系统中的成像位置来确定相对位姿，该方法具有体积小、质量小、功耗低、可靠性高等优点。传统单目视觉算法通过迭代法来求解二次非线性方程[3-4]，测量结果受收敛性和求解速度影响较大。而文献[5]和文献[6]分别采用双目视觉和三目视觉算法，测量基本方程为线性方程组，存在解析解，大大提高了求解位姿的速度和精度以及系统的可靠性。另外，大多数位姿测量算法中均采用基于向量代数的描述方法，通常将刚体运动拆分为平移和旋转两部分，需要分别设计算法来计算两部分操作结果，不仅破坏了运动学的完整性，也增加了算法的复杂度。而几何代数中的马达代数(Motor Algebra)可以很好地解决这个问题。马达代数是对偶四元数的扩充，它将Grassmann扩张代数、Hamilton四元数和复数等统一起来，避免了计算时各种代数语言之间的转换，可以直观地表示几何体的空间运动[7]。因此，马达代数在涉及运动目标位姿处理的相关问题中得到了越来越广泛的应用[7-9]。文献[10]提出了一种基于普吕克直线的交会对接相对位姿确定算法，并通过奇异值分解的方法统一解算出相对位姿值，求解过程复杂，同时对于特征线的安装也要求较高，而且普吕克直线方程的确定仍然需要识别该直线上两个特征点，实际操作难度较大。文献[11]利用对偶四元数描述坐标系间的相对位姿，并设计算法解算出位置和姿态信息，但计算中涉及复杂的矩阵乘法运算，较为繁琐。

基于以上几种方法的研究，本文采用马达代数这一新型数学工具，以两个特征光点确立一条线实体并作为变换基元，统一描述追踪航天器和目标航天器之间的相对位姿，通过马达代数实部和对偶的求解来完成位姿解算。该方法比传统的欧拉角和四元数方法更为简洁有效，且精度较高，具有一定的计算优势和可研究性。

2 测量原理

2.1 坐标系

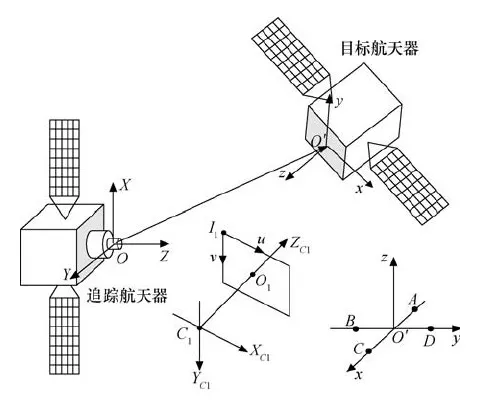
图1 各坐标系的定义 Fig.1 Definition of all coordinate systems

本文通过在目标航天器上设置特征光点，并使用双目视觉测量的方法进行位姿测量。为了便于分析计算，建立的坐标系如图1所示。

1)目标航天器坐标系O′(x,y,z)，简称O′系。该坐标系根据特征光点的位置来定义。设置4个位于x-y平面内且构成正方形的特征光点A、B、C、D，坐标系原点可设置为正方形的中点，x轴沿O′C方向,y轴沿O′D方向，z轴按右手法则确定。

2)追踪航天器坐标系O(X,Y,Z)，简称O系。该坐标系定义在追踪航天器上，其原点定义为追踪航天器的质心，X轴、Y轴、Z轴由追踪器的形状来规定。

4)摄像机坐标系C1(XC1,YC1,ZC1)和C2(XC2,YC2,ZC2)，简称C1系和C2系。摄像机C1和C2与追踪航天器固连，因此两坐标系相对于O系的位姿是已知的。原点C1、C2位于摄像机光心，XC轴和YC轴分别与像素坐标系中u轴和v轴平行，ZC轴沿主光轴方向并垂直于图像平面，光心与图像中心点之间的距离即为摄像机的焦距。

2.2 双目视觉测量原理

双目视觉测量原理如图2所示[12]。追踪坐标系与两摄像机坐标系固连。测量目的是通过空间中一点P在两摄像机图像平面中成像点PC1和PC2的像素坐标，推算出该点在摄像机坐标系和追踪坐标系中的坐标值。

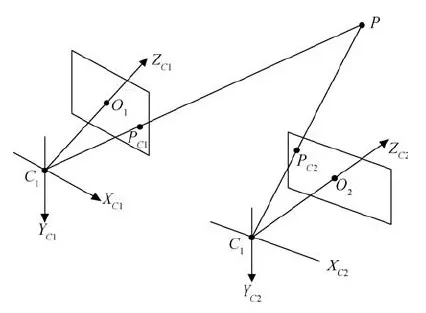
图2 双目视觉测量原理 Fig.2 Principle of binocular vision measurement

P点在追踪坐标系中的坐标为(X,Y,Z)，PC1和PC2的像素坐标分别为(u1,v1)和(u2,v2)。已知两个摄像机的投影矩阵分别为M1和M2，其可由相机的内、外参数决定，不妨假设：

(X,Y,Z)的值可采用文献[5-6]中的最小二乘法来获得，该方法可以避免测量噪声和匹配误差的影响。具体计算形式为

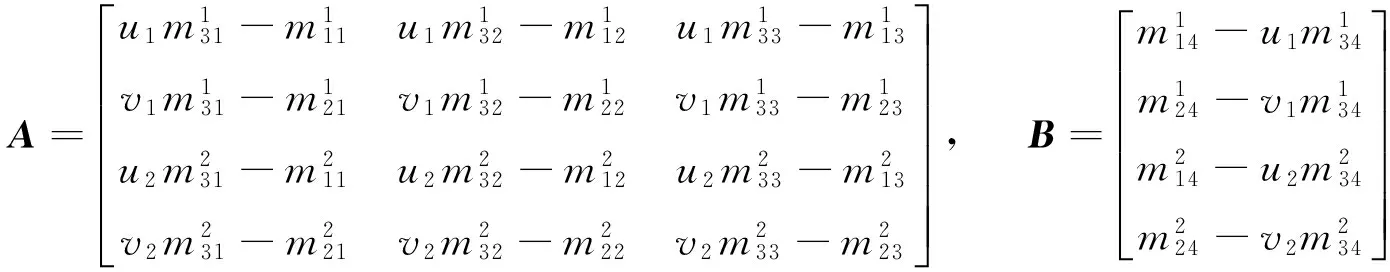
3 位姿解算

若已知特征光点分别在追踪坐标系和目标坐标系中的坐标值，便可以解算出两坐标系间的相对位姿。在传统的基于向量代数的位姿解算方法中，需要求出目标坐标系相对于追踪坐标系的正交余弦矩阵(即旋转矩阵)R3×3和位移向量t3×1。

假设空间一点在目标坐标系和追踪坐标系中的坐标分别为(x,y,z)和(X,Y,Z)，且目标坐标系原点在追踪坐标系中坐标为(tx,ty,tz)，则有

对于方程(2)中R3×3和t3×1的求解，目前有两种方法——解析法和正交法。解析法的主要思想是，分别将4个特征点在目标和追踪坐标系中的坐标代入公式(2)中，得到4组不同的R3×3和t3×1值，再求其平均值。这种方法不仅误差较大，而且不能满足所得旋转矩阵R3×3的正交性。为了解决这个问题，文献[5]提出了正交法，即在4个特征点中任选3个点(A、B、C)构造3个线性无关的向量，如向量dAB，dAC和它们的向量积dAB×dAC，并通过目标和追踪坐标系中向量坐标的对应关系求解旋转矩阵R3×3，最后再对4种情况求取均值。该方法显然可以满足旋转矩阵的正交性，但是在相对位置的求解过程中必须假定4个特征点是对称的，且目标坐标系原点位于它们的中心，要求相对严格。下面介绍一种新的基于马达代数的求解相对位姿的算法。

马达代数空间可由如下所示的基张成：

限于篇幅，作者对于马达代数的具体运算法不再赘述，读者可以参阅文献[7]。

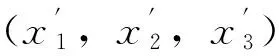
LAB=nAB+ImAB= (xB1-xA1)e2e3+(xB2-xA2)e3e1+(xB3-xA3)e1e2+

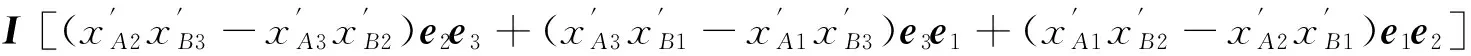
(5)

式中n和n′表示直线AB的方向向量；m和m′为点A和B的外积。

追踪航天器相对于目标航天器的旋量R和平移量t可表示为：

则两坐标系间的相对位姿可统一用如下马达代数描述：

并且有

根据式(9)中直线的运动变化方程，可以列出

式中n和m已知，n′和m′由视觉测量计算得到。不妨假设：

将式(6)、(11)和(12)代入式(10)中第一式，根据马达代数运算法则和等式两边实部、对偶部分别相等的原则，可以写出一组关于未知数r0、r1、r2、r3的线性方程组，用矩阵乘法的形式可表示为

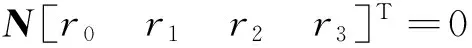
求得旋量R后便可以进一步得到旋转运动所对应的旋转轴和旋转角度。旋量R中r0、r1、r2、r3与旋转轴方向向量nR以及旋转角度θR的对应关系为：

接下来求取目标航天器和追踪航天器之间的相对位移t。将式(10)中第1式代入第2式中可得

式(15)右边值可由计算得知，不妨假设

将式(7)、(12)和(16)代入式(15)，同理根据等式两边实部和对偶部分别相等的原则，可得到关于未知数t1、t2、t3的方程组：

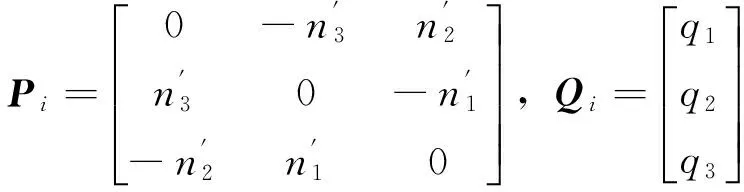
同样地，对于3条直线AB、BC、CD分别可以写出矩阵Pi、Qi(i=1,2,3)，令P=[P1P2P3]T,Q=[Q1Q2Q3]T,则有

式中P为9×3的矩阵；Q为9×1的矩阵。采用最小二乘法求解该方程组，得：

至此，追踪航天器与目标航天器之间的相对位姿M的实部和对偶部便求解完毕。

由上述算法可知，基于马达代数的位姿解算算法将相对位姿中的旋量和平移量有效地统一起来，并将问题简化为两个线性方程组的求解。同时也可以看出，该算法以特征直线为变换基元，既可以满足所得姿态矩阵的正交性，同时对特征点位置是否对称等也并无要求。

4 数值仿真

本节使用Matlab进行数值仿真。已知摄像机镜头焦距为35mm，最高分辨率为4 256×2 832，传感器尺寸为36.0mm×23.9mm，则根据上述参数可以得到摄像机的内部参数矩阵为

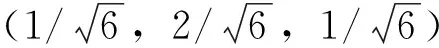
图3显示追踪航天器相对于目标航天器的位姿测量误差均随像素坐标测量误差的增大而增大，与实际情况相符。在像素误差为1像素时，马达代数算法中俯仰角、偏航角、滚动角以及相对位置的测量绝对误差分别为0.09°、0.45°、0.07°和0.003 5m。

图3 情况a仿真结果Fig.3 Simulation under scenario a

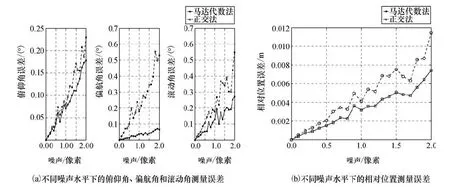
图4 情况b仿真结果Fig.4 Simulation under scenario b

结合两组仿真结果，可知基于马达代数的位姿测量方法的测量误差在航天器交会对接测量精度要求范围之内，因此本文中所提的位姿测量算法是有效的。另外，在同一噪声水平下，马达代数算法相对于向量代数方法具有更高的测量精度，欧拉角测量误差减少了50%左右,且该测量误差受像素误差的影响较小，结果更为稳定。

5 结束语

本文使用马达代数这一新型数学工具，描述了交会对接任务中目标航天器与追踪航天器之间的相对位姿，相对于传统的向量代数描述方法，计算更为简洁。另外，在目标航天器上设置特征光点，并采用双目视觉测量方法，设计并验证了基于马达代数的位姿参数解算算法，最后与正交法的测量误差进行比较。仿真结果表明该方法有效，3个方向上欧拉角的测量误差均在0.5%以内，能够满足航天器对接任务的测量精度要求。同时，该马达代数算法具有更高的精度和稳定性。

[1] 朱仁璋,尹艳. 论空间交会最终平移段制导设计[J]. 中国空间科学技术,2004,24(5):1-8.

ZHU RENZHANG,YIN YAN.Guidance Strategy design for the final translation of space rendezvous[J].Chinese Space Science and Technology,2014,24(5):1-8.

[2] 朱仁璋,汤溢,尹艳.空间交会最终平移轨迹安全模式设计[J]. 宇航学报,2004,25(4):443-448.

ZHU RENZHANG,YANG YI,YIN YAN.Safety mode design of final translation trajectories of space rendezvous[J].Journal of Astronautics,2004,25(4):443-448.

[3] JOHN L J, DECLAR C H, KARIM P W,et al. Vision-based navigation for rendezvous, docking and proximity operations[C]. 4th International Conference on Dynamics and Control of Space Structure，Cranfield University,May 24-28,1999.

[4] 林来兴,李灿. 交会对接最后逼近阶段 CCD 相机的测量方法[J]. 宇航学报, 1994,15(2):24-34.

LIN LAIXING,LI CAN.Method of measurement in the stage of final approaching for rendezvous and docking in space[J].Journal of Astronautics,1994,15(2):24-34.

[5] 张庆君,胡修林,叶斌,等.基于双目视觉测量的航天器相对位置和姿态的测量方法[J]. 宇航学报, 2008,29(1):156-161 .

ZHANG QINGJUN,HU XIULIN,YE BIN,et al.Binocular vision-based relative position and attitude determination between spacecrafts[J].Journal of Astronautics,2008,29(1):156-161.

[6] 钱萍,王惠南. 基于三目视觉测量的航天器交会对接相对位姿确定算法[J]. 宇航学报, 2010,31(6):1575-1581.

QIAN PING,WANG HUINAN.A trinocular vision measurement based relative attitude and position determination algorithm for RVD between spacecrafts[J].Journal of Astronautics,2010,31(6):1575-1581.

[7] EDUARDO BAYRO-CORROCHANO, KOSTAS DANIILIDIS, GERALD SOMMER. Motor algebra for 3D kinematics: the case of the hand-eye calibration [J]. Journal of Mathematical Imaging and Vision,2000,13(2):79-100.

[8] 袁建平,李克昭,岳晓奎. 基于马达代数的航天器视觉相对导航算法研究[OL].[2006-12-25].http:∥www.paper.edu.cn/release-paper/content/200612-371.

[9] 张广军.机器视觉[M].北京:科学出版社,2005:14-32.

ZHANG GUANGJUN.Machine vision[M].Beijing:Science Press of China,2005:14-32.

[10] 李静,王惠南,刘海颖.基于普吕克直线的交会对接相对位姿确定算法[J]. 中国空间科学技术,2013,33(1):69-74.

LI JING,WANG HUINAN,LIU HAIYING.Plucker linear based relative position and attitude determination for RVD[J].Chinese Space Science and Technology ,2013,33(1):69-74.

[11] 钱萍,王惠南. 基于对偶四元数的航天器交会对接位姿双目视觉测量算法[J].宇航学报, 2013,34(1):32-38.

QIAN PING,WANGHUINAN.A binocular vision algorithm based on dual quaternion for relative position and attitude determination of RVD spacecrafts[J].Journal of Astronautics,2013,34(1):32-38.

陈 伟 1992年生，2013年毕业于南京航空航天大学通信工程专业，现为南京航空航天大学导航、制导与控制专业硕士研究生。研究方向为交会对接视觉导航。

(编辑：高珍)

Measurement Algorithm Based on Motor Algebra for Relative Position and Attitude Determination of RVD Spacecraft

CHEN Wei CHEN Zhiming WANG Huinan

(College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016)

Accurate measurement of the relative position and attitude between the active spacecraft and the target spacecraft is the key to the successful completion of rendezvous and docking (RVD) mission. In the traditional vector measurement methods, the position and attitude are usually treated separately, which led to the difficulty of algorithm design and computational complexity.A new binocular vision measurement algorithm based on motor algebra was proposed to uniformly describe the relative position and the attitude of the two RVD spacecraft. This new algorithm has a more concise form and some computational advantages compared to the traditional methods. The relative position and attitude determination problem was simplified to solving two linear equations. Simulation results show that the algorithm can meet the measurement accuracy requirements of RVD missions.

Motor algebra; Rendezvous and docking; Relative position and attitude; Binocular vision;Spacecraft

2014-12-31。收修改稿日期：2015-03-02

10.3780/j.issn.1000-758X.2015.04.011