数值延拓算法应用于直升机配平计算的研究
万绍峰,曹 龙,黄俊森,曹义华
(北京航空航天大学 航空科学与工程学院,北京 100191)
数值延拓算法应用于直升机配平计算的研究
万绍峰,曹 龙,黄俊森,曹义华
(北京航空航天大学 航空科学与工程学院,北京 100191)
直升机配平,本质上为非线性方程组的求解。以UH-60为例,建立直升机非线性飞行动力学模型;通过设置主旋翼轴前倾角为零简化模型,数值延拓得到悬停状态平衡解;以前飞速度为延拓参数,数值延拓完成定直平飞状态的配平计算。使用MATLAB计算平台,配平结果与参考数据吻合较好。结果表明:数值延拓方法简单有效,其结果具有连续性和全面性,易于观察解曲线走向。作为一类计算方法,数值延拓适用于直升机配平计算。
数值延拓;直升机;配平计算;非线性方程组
0 引言
配平计算,是一切飞行器建模分析的基础,也是极其重要的一步。与固定翼飞行器相比,直升机由于存在旋翼气动力,物理模型通常较为复杂;表现在数学中,为强非线性方程组,各个状态变量之间耦合强烈,一般不易求解。
求解非线性方程组,传统的数值方法是牛顿迭代法[1]。因为牛顿迭代法是局部收敛的,所以对于一般的直升机配平问题[2-3],往往给不出合适的初值估计,导致迭代无法收敛。
本文采用动力系统理论[4]中的数值延拓[5-6]方法,以简化模型为基础,数值延拓得到直升机配平结果。
1 理论背景
1.1 动力系统理论
描述一个动力系统通常需要具备两个要素:一是描述系统状态的参量X∈Rn(称为状态点),另一个是给出从一状态点到另一个状态点的对应法则F。具备以上两个要素的系统被称为动力系统。根据对应法则形式的不同,动力系统可分为连续动力系统和离散动力系统。
连续动力系统通常用一个常微分方程组的形式来描述:
式中,X∈Rn,为n维状态向量;Fa(X)∈Rn,为n维向量函数;a∈Rk,为k维参数向量;X′为X的一阶时间导数。
动力系统理论中,分析系统的第一步,是计算动力系统的平衡解。令状态变量导数X′为0,即可得到平衡解,本质上为非线性代数方程组的求解。
1.2 数值延拓算法
k=1时计算系统平衡解。此时,需要求解方程组:
式中,a∈R,为标量参数。注意到方程组包含n+1个未知数,却只有n个方程,此时它的解空间呈现为一条解曲线。
假设已经获得了解曲线上的某一点(X1,a1),并能从该点出发,顺序解出曲线上的其他点(X2,a2)、(X3,a3)、…,那么所有点的集合就是我们需要的解曲线。这一类思想诞生出的算法被人们称为数值延拓。
大部分数值延拓采用预报-校正。为了说明点集合是如何生成的,假设在解曲线上找到一个点(Xi,ai),并且还有点(Xi,ai)处的归一化切向量Vi。那么下一点(Xi+1,ai+1)的计算包含下面两步,见图1。
1) 预测一个新点;
2) 对预测点的校正。
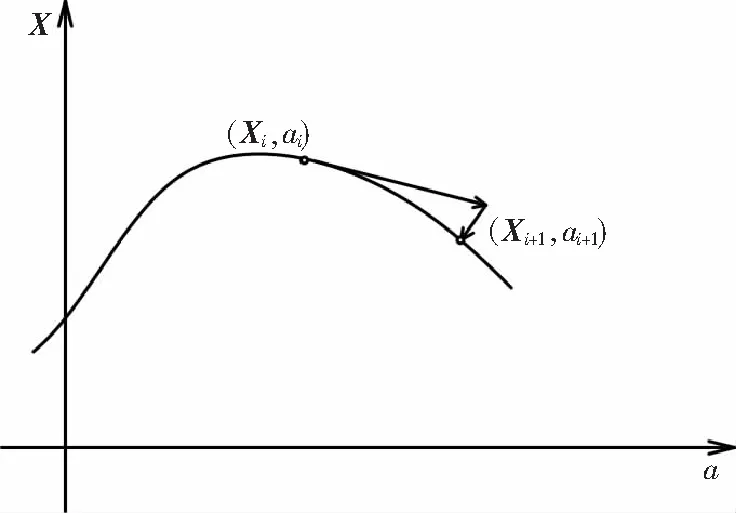
图1 预报-校正法
2 动力学模型
本文选取UH-60直升机建模。
文献[7]详细介绍了一类适用于飞行仿真的单旋翼直升机模型,其中最重要的是旋翼模型。
旋翼作为直升机升力最重要的来源,因为挥舞、摆振等运动存在,推导其气动方程前需要以下假设:
1) 桨叶剖面安装角沿径向线性变化;
2) 不考虑反流区和失速的影响;
3) 桨尖损失系数为1;
4)β(t)=a0(t)-a1(t)cosψ-b1(t)sinψ,挥舞角写成福氏级数时只取到一阶。
文献[7]同时提及了,对于前进比小于0.3的情况,所建模型精度满足后续研究的要求。
为了使该模型同时适用于UH-60直升机,需要对文献[7]中的模型做如下修改[8]:
1) 机身模型
UH-60机身气动力模型使用文献[9]中的风洞数据,通过回归算法得到力和力矩的方程。机体力和力矩均为侧滑角和仰角的函数。
2) 尾桨模型
UH-60尾桨向上斜置20°,不同于常规直升机。为了计算尾桨处的力和力矩,需要引入两个坐标系:斜置尾桨轴系和斜置尾桨风轴系。
尾桨气动力在斜置尾桨风轴系中的表达式和常规尾桨相似,只需替换对应项就能得到尾桨处产生的力和力矩。
3) 水平安定面模型
水平安定面带可变入流角,这有两个目的:一是消除低速时安定面处下洗冲击引起的抬头力矩;二是优化爬升、巡航和自旋下降时的俯仰角。
4) 控制系统模型
UH-60控制系统包括了一个俯仰角偏斜舵机,它改变了纵向周期控制和桨盘倾斜角之间的关系,目的是为了提升飞行器的纵向静稳定性。
将所有力和力矩投影到体轴系,得到飞行器六自由度刚体运动方程。
式中,CB/E为地轴系到体轴系的转换矩阵;X、Y、Z为合力在体轴系的分量;L、M、N为合力矩在体轴系的分量;uB、vB、wB为空速在体轴系下的分量;pB、qB、rB为角速度在体轴系下的分量;IB为直升机转动惯量矩阵;下标B代表体轴系。
3 直升机配平
3.1 悬停状态配平
悬停状态平衡解是所有平衡解中最易求也是最重要的。求解悬停平衡解时,偏航角ψ置为0;空速分量uB、vB和wB,角速度分量pB、qB和rB均为0。将上述条件带入式(3)、(4)中,得到:
式中,X、Y、Z、L、M和N均为四个操纵量δe、δa、δc、δp的函数。
式(5)、(6)联立,六个方程求解六个未知数,包括操纵量δe、δa、δc、δp加两个姿态角θ、φ。求解该问题,可选择牛顿迭代法,但迭代需要给出良好的初值估计,一般情况下很难实现。
本文作者在大量尝试不同初值发现迭代均无法收敛后,改变思路,选择简化物理模型,从简化模型的解出发,得到真实情况下的配平解。
3.1.1 简化模型求解
一般而言,机身、水平安定面和垂直安定面贡献的力和力矩值相对较小,模型简化时可考虑置为0。另外,观察旋翼方程发现,如果将旋翼轴前倾角is置为O,能大大简化方程形式。利用上述条件后,式(5)、(6)可简化为:
上式中,HW、YW、TMR是旋翼气动力分量,均为δe、δa和δc的函数;TTRCW是尾桨升力,仅为δp的函数;K是尾桨斜置角;下标MR代表旋翼,下标TR代表尾桨。
选取δe、δa和δc作为未知数,通过式(7)可依次得到θ、φ和δp的表达式,再带入式(8)中。此时,问题简化为三个方程求解三个未知数,求解难度大大降低。另外,当未知数个数降至3个时,可直接作图观察解的大致范围,给出合理的初值估计,运用牛顿迭代轻松求解,结果见表1。
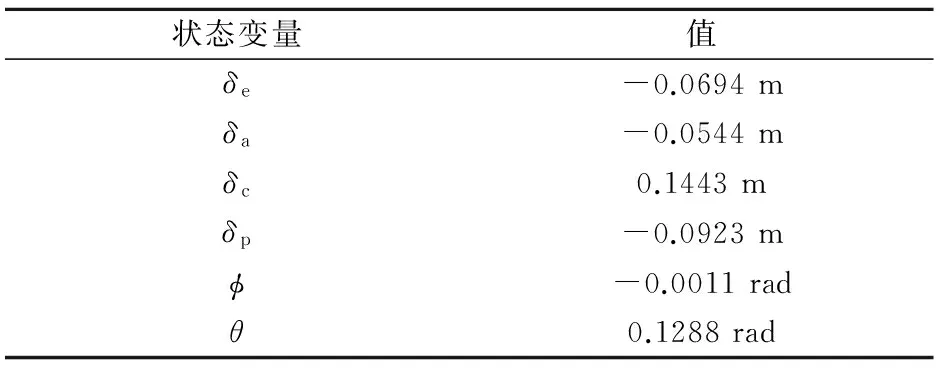
表1 is=0°状态下的解
3.1.2 以is为参数延拓
实际模型中,旋翼轴前倾角值为3°。以表1中is=0°状态下的解为起始点,选择is增大方向为延拓方向,数值延拓,延拓得到的解曲线见图2。
全部的延拓曲线应该有6条,即δe、δa、δc、δp、θ、φ随is变化的曲线,这里只给出了一条。图2中每一个点都对应一个平衡状态,只是旋翼前倾角is不同。如果沿反方向延拓,我们就能得到旋翼后倾时对应的平衡状态。如果减小步长,理论上我们能精确得到任意is时对应的平衡状态。需要注意的是:图2中每一个点都是以前一个点为基础而得到的,整条曲线的得到只需要知道起始点的值(即表1的值)。
从图2中可以看出,以is为延拓参数,总距操纵解曲线先上升后下降,直接得到is=3°状态下的解,见表2。
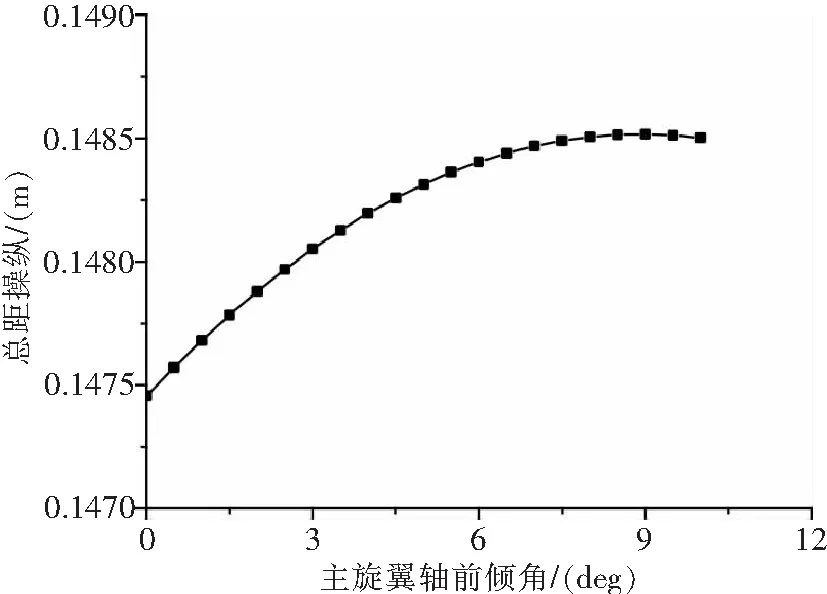
图2 以is为参数延拓

状态变量值δe-0.0443mδa-0.0404mδc0.1449mδp-0.0742mϕ-0.0168radθ0.1349rad
回过来考察式(5)、(6),表2中is=3°状态下的解已非常接近实际悬停配平解,以其为初值估计,运用牛顿迭代轻松求解,得到真实情况下悬停配平解,见表3。

表3 悬停配平解
3.2 前飞状态配平
前飞配平时以前飞地速uE为延拓参数,故需补充相应方程,体现速度在体轴系和地轴系间的转换:
此时,以表3悬停配平解为起始点,选择uE增大方向为延拓方向,数值延拓,延拓得到的解曲线见图3-8,图中提及的参考数据来自文献[8]。
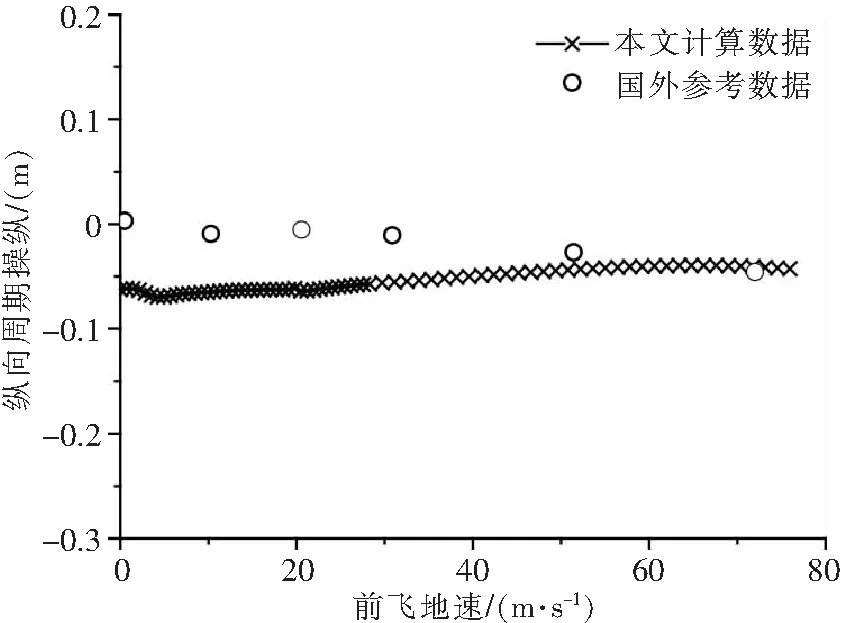
图3 定直平飞纵向周期操纵配平曲线
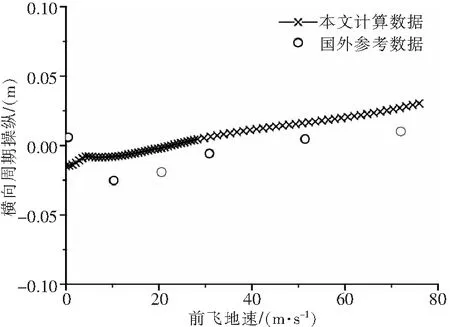
图4 定直平飞横向周期操纵配平曲线
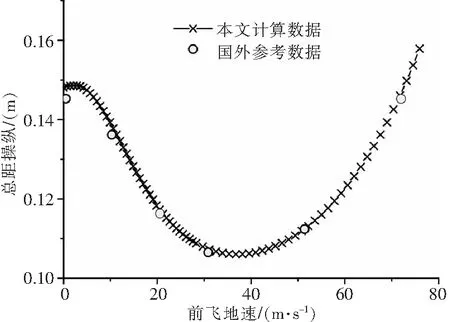
图5 定直平飞总距操纵配平曲线
图3-8中,数值延拓每进行一次预报-校正,就得到解曲线上的一个点,以符号“×”显示。前飞速度0~30m/s阶段步长小,曲线显得密集。由图3-8可以得到各操纵量和姿态角随前飞速度增长的变化趋势,以及各个速度下的配平解。
另外,起始点也可以不选择悬停状态。假设我们知道30m/s时直升机的配平解,只需要沿两个方向数值延拓,也能得到整条解曲线。
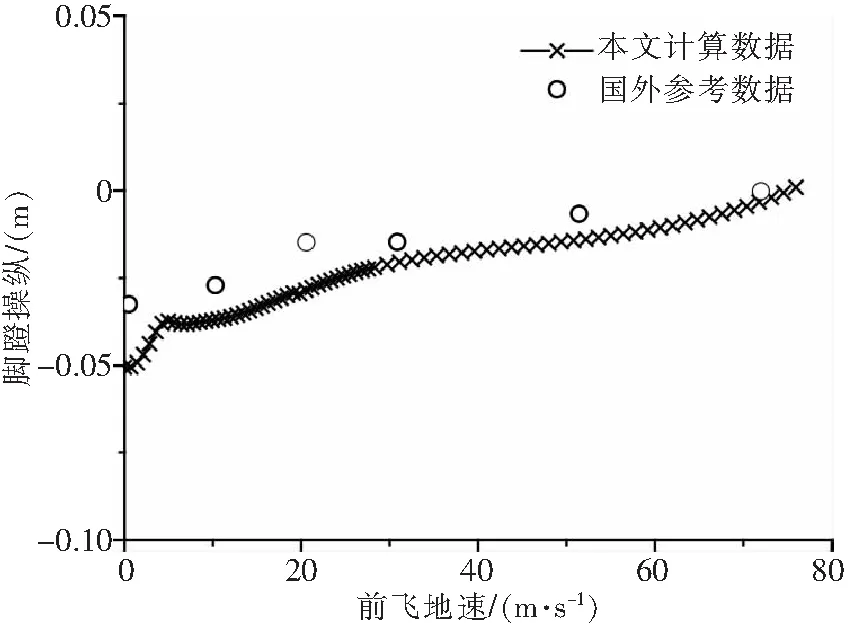
图6 定直平飞脚蹬操纵配平曲线
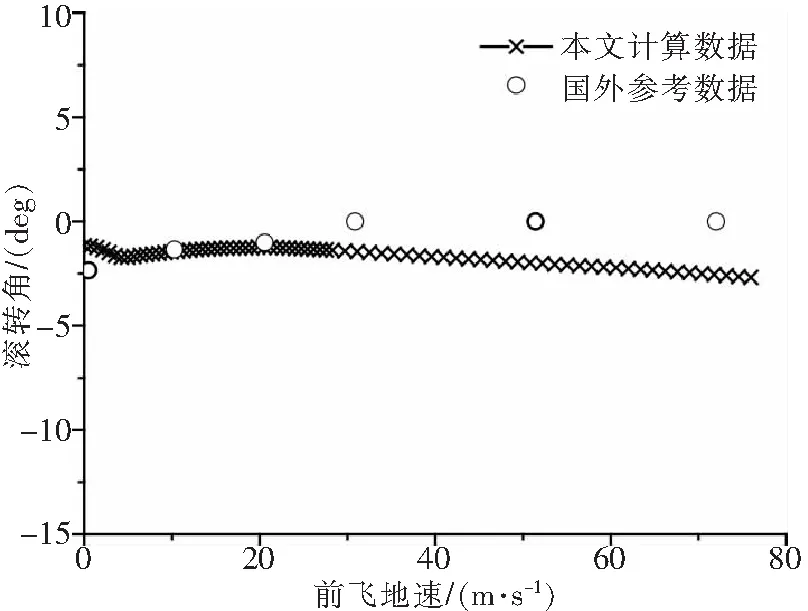
图7 定直平飞滚转角φ配平曲线
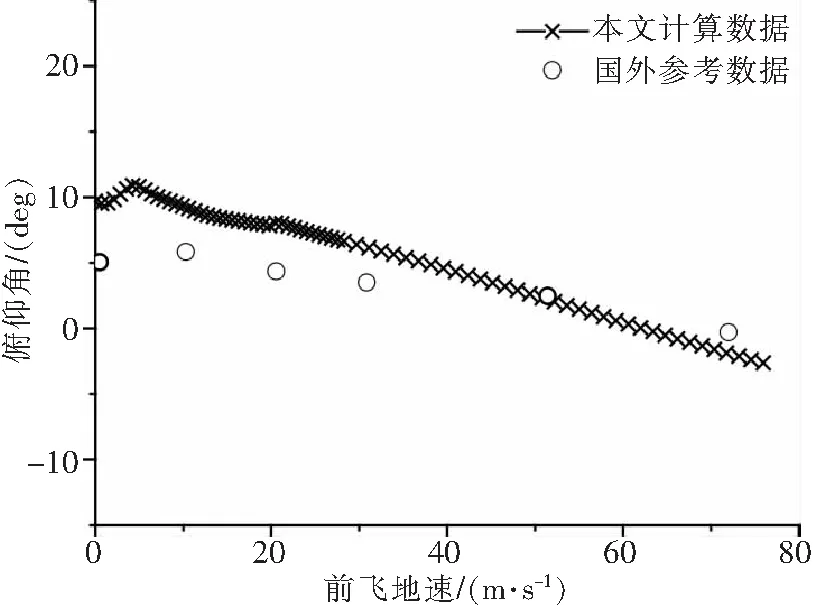
图8 定直平飞俯仰角θ配平曲线
4 结论
本文采用数值延拓方法,完成UH-60直升机配平。从简化状态解出发,数值延拓得到悬停配平解;从悬停配平解出发,数值延拓得到任意前飞速度下的配平解。计算结果与参考数据吻合较好,数值延拓适用于直升机配平计算,得到的配平解连续、全面,计算效率高。
另外,因为数值延拓解的全面性,对于飞行器飞行包线、参数优化等研究也有一定的借鉴意义。
[1] Achar N S, Gaonkar G H. Helicopter Trim Analysis by Shooting and Finite Methods with Optimally Damped Newton Iterations[J]. AIAA Journal, 1993, 31(2):225-234.
[2] McVicar J S G, Bradleyt R. Robust and Efficient Trimming Algorithm for Application to Advanced Mathematical Models of Rotorcraft[J]. Journal of Aircraft, 1995, 32(2):439-442.
[3] Chen F, Omri R. A Highly Robust Trim Procedure for Rotorcraft Simulations[C].AIAA Modeling and Simulation Technologies Conference and Exhibit, 2008.
[4] 张锦炎, 冯贝叶. 常微分方程几何理论与分支问题[M]. 2版. 北京: 北京大学出版社, 2000:105-109.
Zhang Jinyan, Feng Beiye. Geometric theory of differential equations and bifurcation problems[M]. 2nded. Beijing: Peking University Press, 2000:105-109(in Chinese).
[5] Krauskopf B, Osinga H M, Galan-Vioque J. Numerical Continuation Methods for Dynamical Systems[M]. A A Dordrecht, The Netherlands: Springer, 2007:77-95.
[6] Chow C C, Villac B F. Mapping Autonomous Constellation Design Spaces Using Numerical Continuation[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(5):1426-1434.
[7] Talbot P D, Tinling B E, Decker W A. A Mathematical Model of a Single Main Rotor Helicopter for Polited Simulation[R]. NASA TM-84281,1982.
[8] Kathryn B H. A Mathematical Model of the UH-60 Helicopter[R]. NASA TM-85890,1984.
[9] Holett J J. UH-60A Black Hawk Engineering Simulation Program, Volumes I[R]. NASA CR-166309,1981.
Helicopter Trim Calculation by Numerical Continuation Method
WAN Shaofeng,CAO Long,HUANG Junsen,CAO Yihua
(School of Aeronautic Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Helicopter trim calculation is essentially to solve nonlinear equations. The UH-60 helicopter nonlinear flight dynamics model was built. The model was simplified by setting the main rotor shaft forward tilt angle to zero and equilibrium solutions were found by numerical continuation method in hover state. With the forward velocity as a continuation parameter, trim calculation was accomplished by numerical continuation method at the hover in the forward. The whole process was conducted through using the MATLAB software as the computational platform and trim solutions agree well with the referenced data. The results show that, numerical continuation is simple and effective, the results are continuous and full-scale, and it’s easy to watch the trend of the solution curve. As a computational method, numerical continuation is suitable for helicopter trim calculation.
numerical continuation;helicopter;trim;nonlinear equations
2014-09-15
万绍峰(1991-),男,江西南昌县人,硕士生。
1673-1220(2015)02-011-05
V212.4
A

