大型海上风电场中压集电系统拓扑结构的优化方法

魏书荣，符 杨，黄玲玲

(上海电力学院电气工程学院，上海 200090)

大型海上风电场中压集电系统拓扑结构的优化方法

魏书荣，符 杨，黄玲玲

(上海电力学院电气工程学院，上海 200090)

构建了反映海上风电场电气系统成本构成多样、约束条件复杂的优化模型.针对环形结构的中压集电系统优化问题，提出了单亲遗传算法的优化设计方法，并通过实例验证了该优化方法的可行性.

大型海上风电场;集电系统;环形结构;拓扑优化

近年来，环境问题日益严重，清洁能源备受关注.《国家第4阶段机动车污染物排放标准》提前置换、《国家第5阶段机动车污染物排放标准》发布，新能源产业在扶持与规范中并进，其中风力发电已经成为除火电和水电之外的第3大电源，特别是大规模海上风电，在综合节能、环保和减排等因素以及世界各国政府有力的财政政策支持下，已经成为未来风能利用的必然趋势.我国的海上风电虽然起步较晚，但近几年发展迅速，已逐渐在海上风电领域占有一席之地.［1］

大型海上风电场的集电系统贯穿风力发电的始终，包含有大量的电气设备，在发电成本中占有很大的比重.但正因其电气设备繁多，连接方式各异，故存在很大的优化空间，即可以从设备选型、连接拓扑设计、电压等级选择等方面入手进行系统的优化设计.集电系统主要有备用和无备用两大连接方式.目前无备用的放射形连接方式应用较多，有不少学者进行了相关研究.文献［2］采用标准遗传算法对海上风电电气系统进行了优化设计，从风机类型选择、电压等级选择、电缆选型、构成串的方法等方面入手，得出了几套风电场电气系统整体配置的优化方案，并在文献［3］中对算法特性进行了分析.文献［4］以成本最低为目标，利用不同的算法对风电场内部电气连接进行了优化.文献［5］利用FCM及图论技术，对集电系统放射形结构进行了拓扑设计，并通过蒙特卡洛方法评估了设计方案的可靠性.

而有备用的环形网络由于经济成本较高，在之前的海上风电场集电网络规划中使用较少，但对于离岸距离远、容量大的大型海上风电场，由于其可进入性差，采用高可靠性的环形连接方式很有必要.例如，目前英国的大型海上风电场London array海上风电场离岸距离20 km，一期装机容量已达630 MW，其集电网络采用的就是环形网络连接结构.

城市的供水供气管道的拓扑设计原则与海上风电场环形结构集电系统中压电缆拓扑设计原则有相似之处，如不能交叉，力求总长度最短以达到经济最优等.周荣敏等人使用单亲遗传算法解决了树状管网和环形管网优化设计的问题，对集电系统环形结构的拓扑优化设计有一定的参考意义.［6］

本文主要围绕环形结构进行集电系统的优化设计，将管网优化设计思想应用于环形拓扑结构设计中，并在上述两种拓扑结构设计的基础上分别进行设备选型、经济优化和可靠性评估.最后，通过实际海上风电案例对优化设计方法进行了验证.

1 优化模型

本文主要针对环形结构的大型海上风电场集电系统进行优化设计，旨在找到满足可靠性指标的经济最优设计方案.海上风电场电气网络的年投资成本为中压电缆的投资成本(CCB)与变电站投资成本(CSS)之和，即:

优化问题可以描述为:［7］

SS表示变电站.

式中:NSS——变电站数量;

NFi——第s个变电站的馈线数(风机串数);

C(Fs，i)——第s个变电站上第i条馈线的总成本;

C( SSs)——第s个变电站的总成本，本文假设放射形和环形集电系统中变电站成本相等;

ILm——馈线Fs，i上第m段的额定电流;

Irated(cm)——cm类导线的额定电流.

集电系统中第i个馈线上所连的风机个数取决于海底电缆的最大传输功率，同时还要满足电能质量的约束.在开环运行时，环形结构电缆要承担其下游所有风机的出力，因此靠近汇流母线的电缆截面都较大，成本也就有所增加.

在第i个馈线的结构上，每个风机的注入电流为IWTm，第m段电缆的型号为cm，载流量为ILm，所有电流汇入第s个海上变电站的第i个公共连接点Psi，电缆型号cm由以下几个基准确定:负载电流;允许最大电压降落(与第m段电缆的长度Lm相关);最大短路电流.

第s个海上变电站的第i个馈线的造价为:

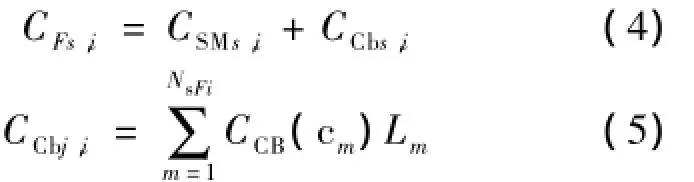
式中:CSMj，i——海底电缆的运输安装费用;

CCbj，i——中压电缆的造价;

CCB(cm)——第m段型号为cm的电缆的单价;

Lm——第m段电缆的长度;

NsFi——第i个馈线上电缆的段数.

集电系统中压电缆的成本是其额定功率的函数［8］:

式中:Irated，m(cm)——型号为cm的电缆的额定电流;

α1，α2，β1——常数，其取值与额定电压Urated，m相关;

Srated，m——第m段电缆的额定功率.

2 优化方法

海上风电场的风机排列布置一般由海面环境、风能特性、海底地质特点等确定，而连接风机的中压电缆的排列布置方式多种多样，风电场采用不同的连接方案，其发电成本、可靠性、系统效率也有很大差异.对于集电系统的拓扑结构而言，风机的集群个数(串数)、集群内风机个数、集群拓扑结构都是影响整个集电系统拓扑结构，进而影响集电系统成本尤其是中压电缆投资成本的关键因素.由此可见，集电系统拓扑结构优化问题是一个多变量非线性组合优化问题.有研究表明，遗传算法对组合优化问题的求解非常有效，能够在较短时间内，以较高概率获得一批最优或接近最优的方案.［8］

本文的优化设计方法流程如图1所示.

图1 集电系统优化设计流程

在基本遗传算法中，交叉点是随机选择的，两个父代进行基因交叉后得到的子代极有可能出现某些节点重复、另外一些节点丢失的情况，这样就违背了每个节点只能通过一次的原则，并且这种病态个体不仅不是可行解，而且还有可能通过恶性竞争淘汰正常个体，使遗传算法最终得到错误解.［9］此外，在实际应用中，个体基因链较长，通过交叉算子产生可行个体的概率很小.而单亲遗传算法中父代只有一个个体，该个体经过一定的遗传操作产生新个体，并且保证新个体是可行解.因此，根据集电系统优化设计的具体特点，本文放弃了传统的双亲遗传算法而采用了单亲遗传算法.现就遗传算法的具体操作过程描述如下.

2.1 编码

海上风电场集电系统拓扑优化设计实质上是风机节点的组合优化问题.考虑到风机数量可能较大，二进制编码位数较多，整数编码对于节点组合优化问题简单明了，因此本文采用了整数编码方式;采用环形结构时，风机串一般都有多个，所以需要将风机进行分组.综上所述，本文针对集电系统拓扑结构优化问题采用了染色体对并行遗传的方式，一个染色体携带路径信息(即路径染色体)，另外一个携带分组信息(即断点染色体)，两个染色体都采用简单直观的整数编码:对风机进行编号，风机编号按一定顺序组合起来就是路径染色体的基因组;断点染色体中的整数组用于表示断点在路径染色体中的位置，若分组数为n，则断点染色体只需n-1位.假设20台风机分成3组，3组风机个数分别为7，7，6，染色体对的编码方式如图2所示.

根据风机分组的要求，断点染色体可以有不同的设置.如果要求每组内的风机数相当，即断点位置固定，此时断点染色体中的整数是固定的;如果要求每组风机数在大于最小风机数的情况下寻优，则断点染色体中的整数是变化的.

图2 染色体对的编码方式

2.2 适应度函数设计

在寻优过程中，表征电缆路径的生成树或旅行商路径确定后，每段电缆所带风机数和流经的最大短路电流也随之确定，从而可以求出每段电缆的载流量，并使用最大短路电流进行校验.电缆型号确定后，根据选定的电缆型号、电缆单价及其长度，即可算出电缆的造价，以此作为适应度值.

考虑到连接电缆不能有交叉这一实际问题，本文在适应度函数中加入了与交叉次数正相关的惩罚函数.通过设置相应的参数值，得到的优化设计中必然不会出现电缆交叉.

2.3 遗传算子设计

本文采用单亲遗传算法以解决风机优化组合问题，染色体数组中任何一个数值都不能改变，对其的遗传操作只能改变数组的组合排序.因此，针对这一特殊要求，本文采用了如下3个算子.

(1)换位算子对所选择的个体基因组上的任意一对基因进行交换，如图3所示.被交换的基因随机产生.

图3 换位算子的基因换位示意

(2)逆转算子将所选择的个体基因组上的任意一段基因进行逆转，一次性地完成从一个母体突变为一个新子体，如图4所示.

图4 逆转算子的基因换位示意

(3)平滑算子将所选择的个体基因组上的任意一段基因的最后一位移至该段基因第一位，其他基因向后平移一位，如图5所示.该基因段是随机选择的.

图5 平滑算子的基因平移示意

与传统的遗传算法相比，单亲遗传算法的特点在于:在子代群体产生的过程中，每个子体都只有一个母体，通过对母体执行如上所述的遗传操作，产生出一个具有不同性状的新个体.这些遗传操作不仅可以保证新一代个体具有成为可行解的基本特性，而且还能提高对解空间的搜索能力.

2.4 进化策略设计

(1)初始化策略根据风电场风机及海上变电站的排布特点，先对风机进行横坐标方向上的硬划分，即按横坐标分为M组，然后再以组为单位进行路径染色体的基因组合，其中每组内的风机顺序是随机的.另外在环形结构设计中，对个别路径染色体中每组内的风机进行了近似最优Hamilton圈的计算，按一定顺序排布了基因组中的编号.通过验证相对于随机生成的初始群体，初始化后的群体收敛速度明显提升.

(2)代间竞争策略在遗传进化过程中，为保证群体性能的优越性，采用了代间竞争的竞争机制，即在保持群体规模不变的情况下，亲代和子代一起进行生存竞争，选择最优的若干个体作为新一代群体的一部分.

(3)混合选择机制既保留了优先选择机制又包含了平等随机选择机制，这样既保证了种群的优良性又不丢失多样性.本研究的具体实施方式为，每8个个体为一组，从中选择最优个体，并随机抽选另外一个个体，最优个体直接保留进入下一代，此外最优个体和随机个体分别进行换位、逆转、平滑等遗传操作，产生新个体.这种混合选择机制有利于扩大搜索空间，提供单亲遗传算法的全局搜索能力.

(4)进化终止策略遗传算法是一种反复迭代的搜索方法，它通过多代进化逐渐接近最优解，但不一定是最优解，因而必须事先给定进化终止条件.在遗传算法中一般采用最大遗传代数作为进化终止条件，以免陷入无限循环.本文考虑电缆排布不交叉的实际问题，在给出最大遗传代数的同时，将是否添加与交叉次数相关的惩罚项的两个代价的差值是否为零作为辅助终止条件，当两者差为零，即没有交叉时终止遗传.

3 案例分析

为证明所提的集电系统优化设计方法的可行性，对海上风电场进行了实例分析.

3.1 风电场描述

该海上风电场含56台风机，风机的具体参数见表1.风机坐标及海上变电站坐标已确定，风电场排列布置如图6所示.

表1 单台海上风电机组参数

图6 该海上风电场风力发电机组排列布置

集电系统中的连接电缆采用35 kV海底中压电缆，电缆数据见表2.

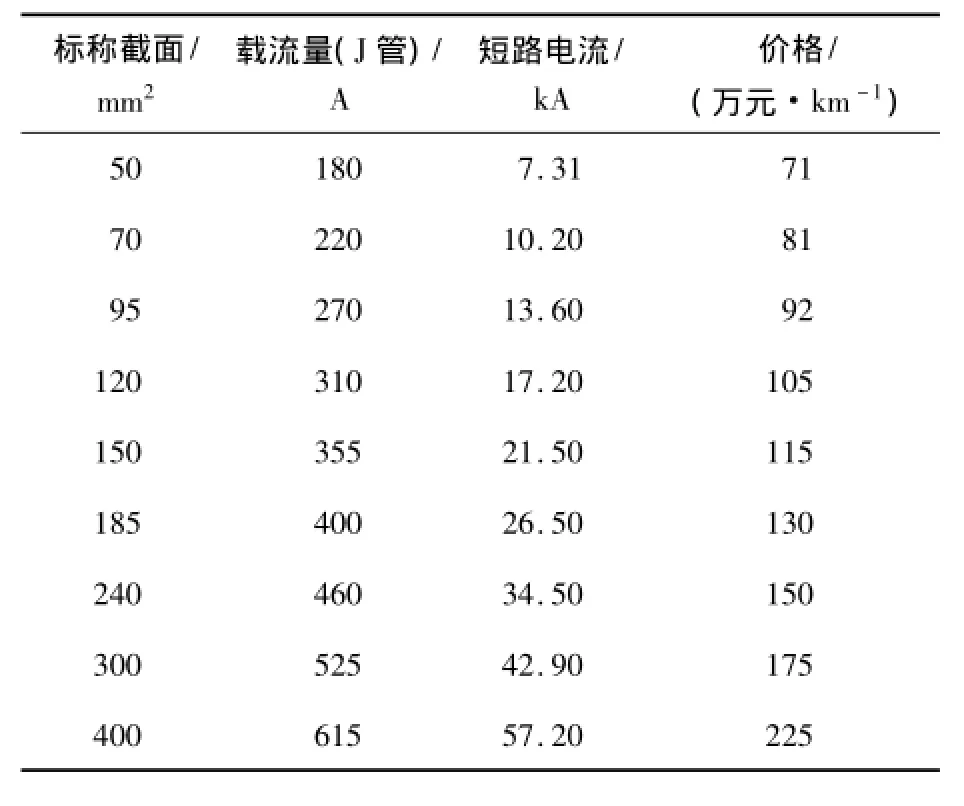
表2 电缆参考数据

3.2 优化设计结果

利用如上所述的优化设计方法对该海上风电场进行了优化设计，考虑风机间连接方式(环形)、风机串数目、设备型号等几个影响集电系统成本的关键要素，最终得到了以环形结构为基础的分为5串和6串的两种集电系统拓扑结构，如图7所示.两种方案的经济性及可靠性数据如表3所示.

由表3可知，环形结构为5串的风机的经济性和可靠性都较好.相比于放射形结构，环形结构虽然经济成本较大，但其对可靠性的提升也是显而易见的.由此可知，对于可靠性要求严格的风电场，环形结构应是有利选择.

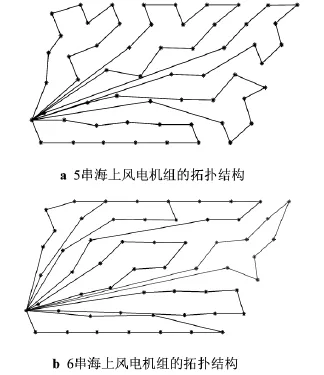
图7 两种拓扑结构

表3 两种方案的经济性及可靠性分析结果

4 结论

(1)建立了优化模型，以反映海上风电场电气系统成本构成多样、约束条件复杂的特性.

(2)提出了解决拓扑结构设计、设备选型与校验及经济成本优化等问题的具体方法，并采用单亲遗传算法对优化模型进行了求解.

(3)通过实例对该优化设计方法进行验证，结果表明，本文提出的集电系统拓扑结构优化设计方案的经济性、可靠性数据详尽明确，可以作为海上风电场规划优化的参考.

［1］全球风能理事会.全球风电市场发展报告2012［J］.风能，2013(4):32-36.

［2］ZHAO M，CHEN Z，BLAABJERG F.Optimisation of electrical system for offshore wind farms via genetic algorithm［J］.IET Renewable Power Generation，2009，3(2):205-216.

［3］ZHAO M，CHEN Z，HJERRILD J.Analysis of the behavior of genetic algorithm applied in optimization of electrical system design for offshore wind farms［C］.Proc.32nd Annu IEEE IECON，2006:2 335-2 340.

［4］HUANG L，FUY，GUOX.Optimizationofelectrical connection scheme for large offshore wind farm with genetic algorithm［C］.Proc.Int.Conf.Sustainable Power Generation Supply(SUPERGEN)，Apr.2009:1-4.

［5］陈宁.大型海上风电场集电系统优化研究［D］.上海:上海电力学院，2011.

［6］周荣敏，雷延峰.管网最优化理论与技术——遗传算法与神经网络［M］.郑州:黄河水利出版社，2002:53-105.

［7］符杨，吴靖，魏书荣.大型海上风电场集电系统拓扑结构优化与规划［J］.电网技术，2013，37(9):2 553-2 559.

［8］FRANCISCO M，GONZ＇alez-Longatt，PETER Wall，et al.Optimal electric network design for a large offshore wind farm based on a modified genetic algorithm approach［J］.IEEE Systems Journal，2012，6(1):164-172.

［9］李茂军.单亲遗传算法理论及应用［D］.湖南:湖南大学，2002.

(编辑 胡小萍)

Topological Optimization Method of the Electric Power Collection System for an Offshore Wind Farm

WEI Shurong，FU Yang，HUANG Lingling
(School of Electrical Engineering，Shanghai University of Electric Power，Shanghai200090，China)

The complex optimization model is established，in which the electrical system cost of offshore wind farm is diversity，and constraint condition is complex.Single Parent Genetic Algorithm (SPGA)method is used to solve the ring structure optimization problems of the electric power collection system.Then the feasibility of the optimization method is verified by examples.

offshore wind farm;collection system;ring structure;topological optimization

TM614

A

1006-4729(2015)03-0201-05

10.3969/j.issn.1006-4729.2015.03.001

2015-05-18

魏书荣(1980-)，女，副教授，湖北钟祥人.主要研究方向为海上风电场规划设计及运行维护.E-mail:wsrmail@163.com.

国家自然科学基金(51177098);上海绿色能源并网工程技术研究中心资助项目(13DZ2251900);上海市重点支撑攻关计划项目(13160500800).