若干关于调和数的等式

申玲玲，郜静霞

(重庆师范大学 数学科学学院，重庆 401331)



若干关于调和数的等式

申玲玲，郜静霞

(重庆师范大学 数学科学学院，重庆 401331)

摘要本文利用发生函数理论的方法得到一个新的关于调和数的等式，此等式还包含贝尔多项式，其中定义的Hspan(m)是关于m和n的调和数，利用这个等式并用自然的方法可以得到一系列等式。

关键词调和数；贝尔多项式；等式

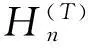
关于贝尔多项式Yn=Yn(x1,x2,…,xn)有：

(1)

在Riordan[1]中就给出了一些相反的数对，本文就用到其中一个：

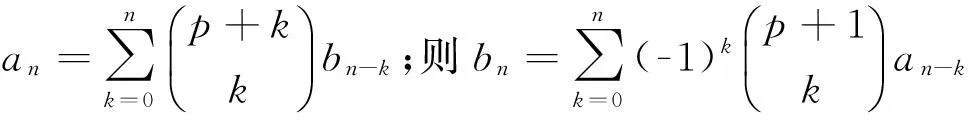
1一个新等式

在文献[2]中Zave给了一个等式及证明，参照该方法将m的范围扩大得到了一个新的等式。

定理1.1若m∈R且m∉{1,2,3,…}，r∈N,那么

(2)

证明利用发生函数理论和泰勒展开式有：

当m=(0, -1, -2, -3, …)可以得到定理1.1[3]。

其中

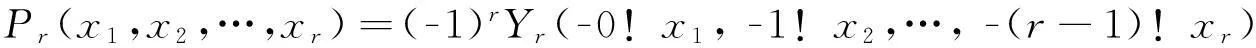
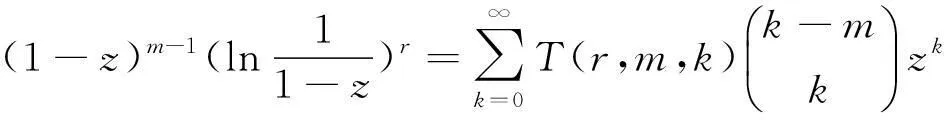
(3)

2应用

定理2.1若n,u,v∈N,p,q∈R且p,q∉{1,2,…},则

证明明显地，可以得到：

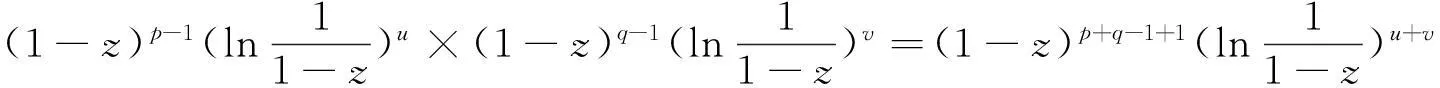
将式(3)代入左右两边，对比两边的系数便可得到。

为了更好的展示定理2.1，给出一个特殊的例子：

当u=v=0，有：

如果只分解一个因数(1-z)m-1可以得到另外的一个定理：

定理2.2若m,p∈R且m,p∉{1,2,…}，则

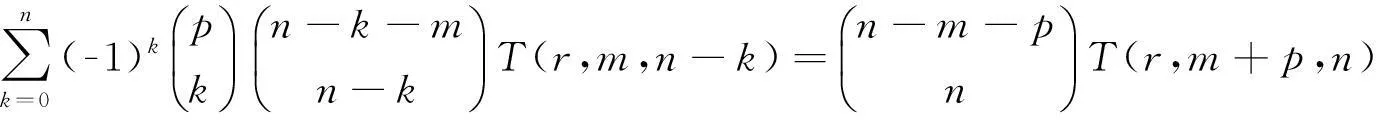
证明由式(3)可得：

同理可得：

交换和的顺序并对比系数便可得。

当r=0,有：

定理2.3若r,k∈N,m∈R且m∉{1,2,…}，n≥1,r≥1则

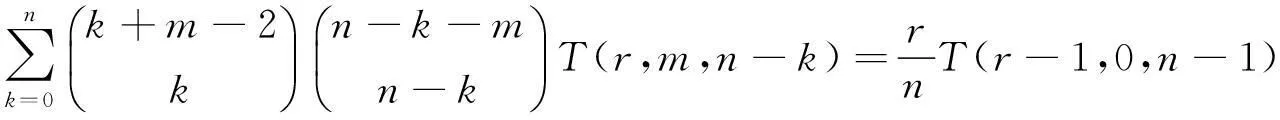
证明明显地有

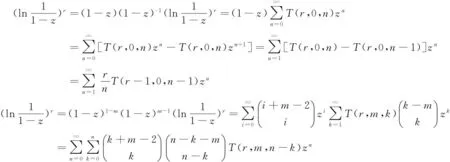
对比这两个等式的系数即可。

特别地，当r=1有

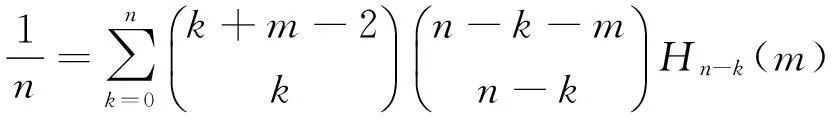
定理2.4若m∈R且m∉{1,2,…}，r,s∈N,s≥1,则

证明将式(3)和定理2.4证明过程中的一个等式代入下面等式：

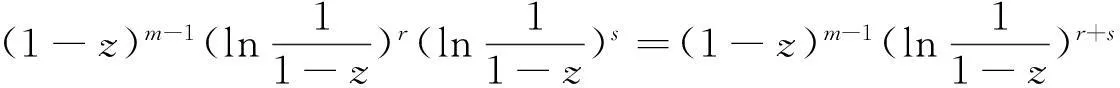
对比两个等式的系数即得。

特别地，当r=0,s=1有

利用数对(1)可得

以上定理是由分解因数得到的，在定理1.1的证明过程中，有一个特殊的等式，利用这个等式可以得到定理2.5。

定理2.5若r,k∈N,m∈R且m∉{1,2,…}，r≥1,k≥1,则

(4)

证明在定理1.1的证明过程中有这样一个结果

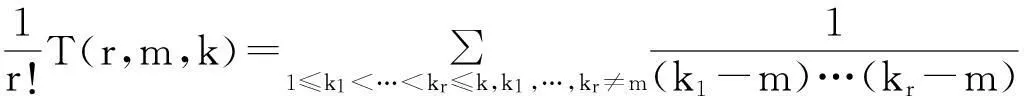
分解定理2.1中组合等式左边的因数可以得到新的定理，在它的左边添加一个特殊的因数也可以得到一个新的定理。

3结论

通过以上的方法得到了新的定理，但可以发现这些定理的限制条件太多，应用也不够广泛。希望以后可以有一些新的方法来将这些限制条件去掉来使这些定理的应用更加地广泛。

参考文献:

[1]Riordan J. Combinatorial identities[J]. R E Krieger Pub Co,1979.

[2]Zave D A. A series expansion involving the harmonic numbers[J]. Information Processing Letters,1976,5(3):75-77.

[3]Spieβ J. Some identities involving harmonic numbers[J]. Mathematics of Computation, 1990,192:839-863.

编辑王菊平

Some equations involving harmonic numbers

SHEN Ling-ling, GAO Jing-xia

(School of Mathematics Sciences, Chongqing Normal University, Chongqing 401331, China)

AbstractIn this paper we get a new identity involving harmonic numbers by means of occurring functions, this equation includes Bell polynomial. LetHspan(m) denote them,nharmonic number. These identities are generalized in a natural way by means of generalized functions.

Key wordsharmonic numbers; Bell polynomial; equations

作者简介申玲玲，女，河南安阳人，在读硕士研究生，主要研究方向为基础数学。

收稿日期2014-12-28

doi10.3969/j.issn.1003-8078.2015.06.05

中图分类号O1

文献标志码A

文章编号1003-8078(2015)06-0019-04