基于PSO-LR的多输入多输出系统预编码方案
张春凯
(江苏食品药品职业技术学院 计算机应用技术系,江苏 淮安223003)
基于PSO-LR的多输入多输出系统预编码方案
张春凯
(江苏食品药品职业技术学院 计算机应用技术系,江苏 淮安223003)
为了提高多输入多输出系统的通信质量、降低误码率,针对格基约减(Lattice Reduction,LR)算法格基优化的难题,提出一种粒子群算法优化格基约减的多输入多输出系统预编码方案(Particle Swarm Optimization-LR,PSO-LR)。该方案将初始格基置乱产生粒子群算法的初始粒子群,然后采用粒子之间的信息共享和交流操作产生性能最优的新格基,最后对算法的性能进行理论分析,并通过仿真实验测试其性能。结果表明,相对于同类其它方法,PSO-LR算法有效地降低多输入多输出系统通信的误码率,提高了通信质量。
多输入多输出;预编码;粒子群算法;格基约减
0 引言
随着无线通信技术的发展,宽带数据业务量急增,用户对数据传输率和通信容量要求越来越高,然而无线通信系统的频谱和发射功率十分有限,如何充分利用有限的资源来满足用户成为当前一个重要研究课题[1]。多输入多输出(Multiple Input Multiple Output,MIMO)可以在不损伤频带和不增加发射功率条件下,成倍提高系统的通信容量,较好地解决了频带资源紧缺难题,因此多输入多输出技术成为当前无线通信领域的研究热点,受到人们越来越多的关注[2]。
在多输入多输出系统通信过程中,由于受到多用户、多天线造成的信道干扰,严重影响了通信质量,成为多输入多输出系统应用中的瓶颈问题[3]。为了解决该难题,需要采用一定的技术对接收机和发射机两端信号进行处理,预编码技术在这种背景下应运而生[4]。预编码的基本思想为:首先采集发射端的信道状态信息,然后采用预编码矩阵对信号进行预处理,消除用户之间的干扰,提高系统吞吐率,降低系统误码率。预编码算法分为两类:线性和非线性预编码,其中线性预编码算法主要有基于迫零(zero forcing,ZF)和最小均方误差(minimum mean square error,MMSE)两种准则[5,6],它们具有成本低、复杂度低等优点,在理想条件下可以降低用户干扰,但是通信性能比较差;非线性的预编码算法主要有模代数预编码 THP(Tomlinson-Harashima Precoding)等,THP算法融合了取模操作和串行干扰消除技术,可以更好地抑制噪声、误码率。然而,当信道状态矩阵发生根本性变化,THP算法的误码率急剧上升,为此有学者提出了基于格基约减算法(Lattice Reduction,LR),利用减格技术改良发射端信道状态矩阵,可以有效抑制噪声,提高统性能[7]。LR算法是从一组给定的基出发,对其进行不断变换,然后找到一组长度更短的向量,由于初始基不同,LR算法得到新基长度也不同,因此LR算法的效率和输出基质量与初始基选择密切相关[8]。粒子群算法(Particle Swarm Optimization,PSO)是一种模拟鸟群觅食行为的群智能算法,其将问题的可行解看作粒子群索,然后每一个粒子根据自身和群全的飞行经验在解的空间飞行,找到最优解,为LR算法初始基的确定提供了一种新的研究思路[9]。
通过上面的分析,为了提高多输入多输出系统的通信质量,降低数据传输的误码率,本文提出一种粒子群算法优化LR的MIMO系统预编码方案(PSO-LR),最后通过仿真实验验证了其有效性和优越性。
1 MIMO系统预编码模型
多输入多输出通信系统的发送端和接收端包含多个天线,其工作原理为:首先信号数据流通过发送端输入到处理模块中,进行编码、调制和加权,然后将处理后的数据送到发射天线,天线对信号进行解调、匹配滤波、译码等处理,最后接收端输出信号。设多输入多输出通信系统的接收端有K个移动用户,每个移动用户拥有Nrk根天线,预编码技术是对多输入多输出通信系统发射端的信号进行预处理,使发射信号更好的适应信道状况,提升系统性能,预编模型结构具体如图 1所示[10]。
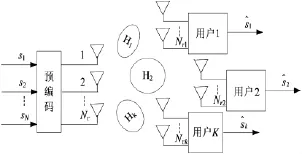
图1 多用户MIMO系统的预编码模型
设wk表示用户k的预编码矩阵,那么用户k接收到的信号向量可以表示为:
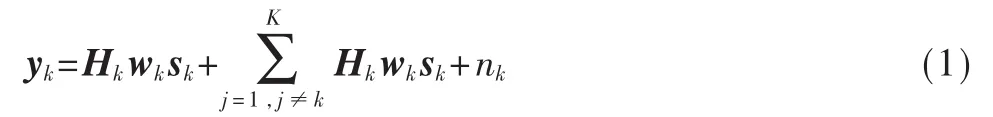
其中,Hk表示用户k的信道矩阵,sk表示发射信号的矢量,nk表示高斯噪声。
式(1)可以简化为:

其中,W=[w1,w2,…,wK],S=[s1,s2,…,SK]T。
预编码技术主要是消除多用户之间干扰,预编码矩阵可以采用如下公式计算得到。

式中,α是功率控制因子。
LR算法的核心是将H进行分解,得到正交性更强的矩阵 Hreal和一个幺模交换模矩阵 U,可以表示为:

LR算法的关键点是找到最优的矩阵 Hreal,其与 H可构成相同的格空间,因此本文将搜索能力强的粒子群算法引入到LR算法中找到得更优的矩阵H,以提高多输入多输出系统的通信质量[11]。
2 MIMO系统预编码方案
2.1 THP预编码方案
THP预编码是一种性能较优的非线性预编码方案,融合了算术取模和串行干扰消除技术,在判决反馈均衡器端进行取模操作,取输入信号在星座图上的边界作为模,然后把均衡器的输出映射到输入端信号的星座图上,有效降低信号发射功率,抑制传输过程中噪声增强,其系统框架如图2所示,其中,Mod表示取模操作,n表示加性噪声,B为对角线元素为1的上三角矩阵,G是补偿矩阵,主要用于消除取模操作的影响[12]。

图2 THP预编码系统框架
由于当信道状态矩阵发生根本性变化,THP预编码算法的误码率将急剧上升,为此有学者将LR算法与THP预编码算法结合,产生LR-THP预编码算法。采用LR算法将信道状态矩阵H转换成为更好的新基,然后据QR分解理论产生两个矩阵,这样低级的子信道就会对高一级的子信道造成干扰。因此,可以通过串行干扰消除技术消除子信道间干扰,并采用THP取模操作将发射信号重新限制在输入信号的范围之内。
LR算法只能在多项式时间内找到一个长度不超过格中最短向量长度 2(n-1)/2倍的向量,为了获得更优的格基,所以本文提出采用粒子群算法对LR算法的格基进行优化,以获得更加理想的传输信息。
2.2 LR算法
2004年,LENSTRA A K等提出了一种性能优异的格基约减算法(LR),设存在一个矩阵B,对B做QR分解得到B+QR,如果三角矩阵R满足下列条件:

则可称B是格基约减的。
经过LR算法约减之后能得到近似于最短向量的短向量,而且经过LR算法约减之后得到的新基的正交偏离度得到了极大的改善,即正交性更强[13]。
2.3 粒子群算法
在标准粒子群算法中,每个粒子均具有自己的位置和速度,n维解空间中每个粒子的位置代表优化问题的一个可能解。每个粒子根据自身的经验和群体的经验调整速度和位置,具体如下:
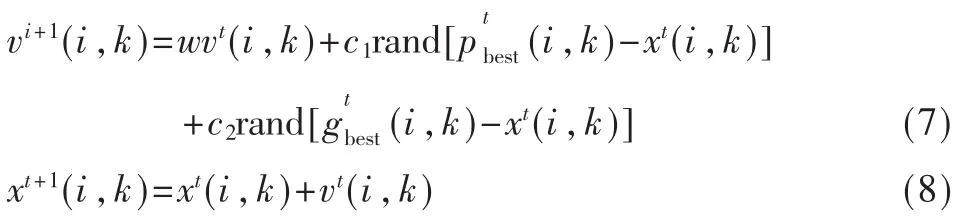
式中,ω称为惯性权重,c1、c2为学习因子,pbest表示粒子本身经历过的最好位置,gbest表示种群经历过的历史最好位置。
2.4 PSO-LR预编码方案流程
初始格基的排列顺序不同,LR算法找到的新格基也不相同,因此,可以通过置乱初始格基,得到多组新的格基,以这些格基作为候选解,然后采用粒子群算法找到最优的格基。
(1)粒子群的初始化。对于格基约减算法而言,初始格基只有一个,即只有一个初始解,只有通过对这一组格基进行变换来生成其它的候选格基,构成初始粒子群,具体方式为。
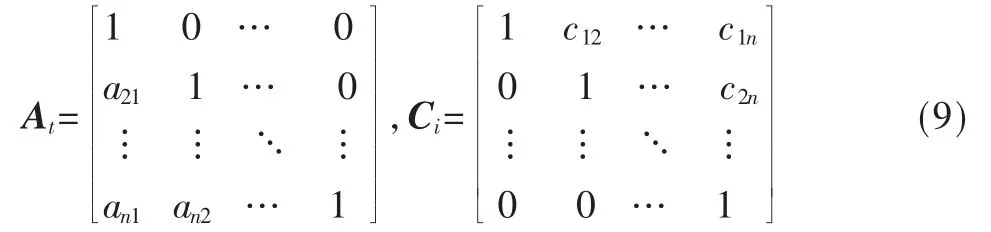
根据Bi=UiB就产生了m组基,便完成初始种群产生。
(2)适应度函数设计。适应度值越差表示该个体的生存能力越弱,越易被淘汰;反之表示该个体的生存能力很强。个体适应能力优劣通常采用适应度函数进行描述,因此,在粒子飞行过程中,适应度函数指导种群进化的方向,也是指引最优解的搜索空间。设基格L的其中一组约减基b,其约减基首向量长度为 y1(b),约减基的平均向量长度为 y2(b),那么适应度函数定义为:
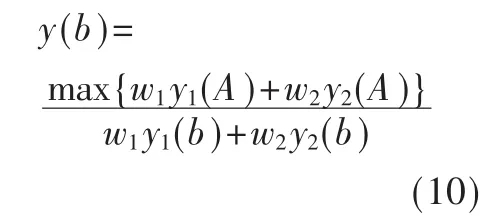
式中,w1、w2表示权值,A表示种群的集合。
本文的粒子群算法优化LR算法的流程如图3所示,工作步骤如下:
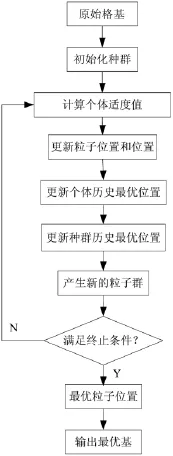
图3 PSO-LR的工作流程
步骤1:将一组格基b1,b2,…,bn进行置乱,产生包含m个体的初始粒子群。
步骤2:将每一个粒子的适应度值与个体历史最优值进行比较,如果更优,则用当前粒子位置替换自身历史最优位置。
步骤3:将每一个粒子的适应度值与群体历史最优值进行比较,如果更优,则用当前粒子位置替换种群历史最优位置。
步骤4:根据式(4)和式(6)更新粒子的速度、位置。
步骤5:如果满足算法终止要求,则输出适应度最高的一组格基,否则返回步骤2继续进行优化。
3 仿真实验
3.1 仿真环境
为了测试本文预编码算法的性能,在 AMD Athlon (tm)II X2 250 3.00 GHz CPU、4G RAM的 Windows XP系统平台上,采用 MATLAB 2009b进行仿真实验,以测试算法在4×4多输入多输出系统,4QAM和16QAM调制方式下的性能。信道模型采用静态瑞利平坦衰落信道,每个用户的发射功率相等,仿真次数为2 000,在相同配置条件下,与采用LR-THP、MMSE-THP算法进行对比实验。
3.2 结果与分析
LR-THP、MMSE-THP以及PSO-LR算法的仿真结果如图4、图5所示。

图4 三种算法的性能比较(4QAM)
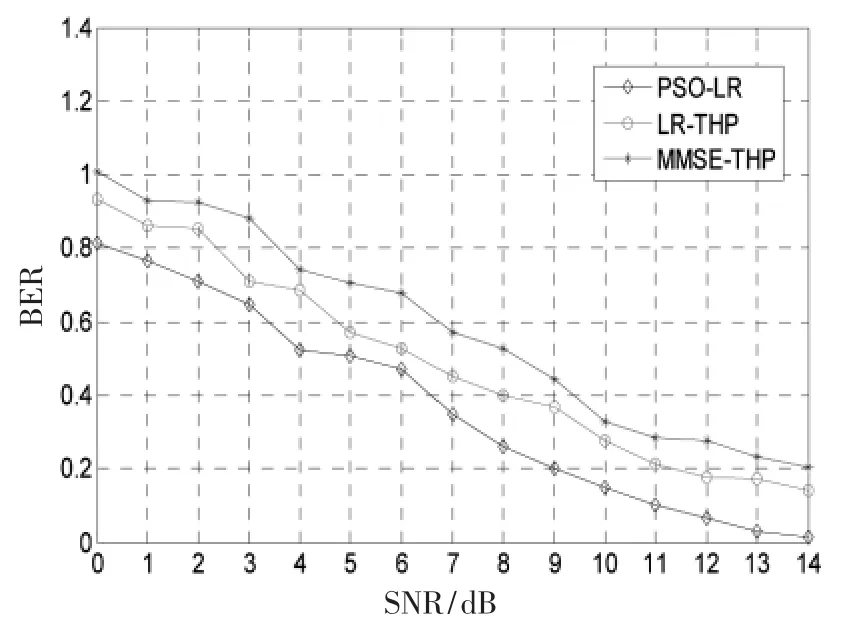
图5 三种算法的性能比较(16QAM)
对图4、图5进行对比和分析,可以得到如下结论:
(1)当信噪比较小时,LR-THP、MMSE-THP以及PSO-LR算法的性能相差不大,随着信噪比增加,3种算法的误码率(BER)不断下降,相对于MMSE-THP算法,LR-THP、PSO-LR算法的性能具有明显的优势,这主要是由于LR-THP、PSO-LR算法采用了基于格基约减的 THP预编码方案,通信质量得以明显改善,对比结果验证了采用基于格基约减预编码方案的有效性和优越性。
(2)相对于 LR-THP算法,PSO-LR算法的误码率更低,这主要是因为采用粒子群算法对初始格基进行优化和选择,可以得到长度更短的向量和质量更高的一组新基,从而提高了格基约减算法的运行效率,一定程度保证了传输数据的可靠性。
4 结束语
本文针对当前格基约减算法存在的不足,充分利用粒子群算法的优点,提出了一种基于粒子群算法优化格基约减的预编码机制,并通过仿真实验测试算法的性能。仿真结果表明相对于传统预编码方案,在相同条件下,PSO-LR预编码机制有效降低了误码率,提高了通信质量。然而在现代移动通信中,不仅要考虑通信质量,同时还考虑算法的复杂度,因此如何更好的平衡性能和复杂度之间的关系是我们将来研究的重点。
[1]范文兵,赵龙贺,王绿静.单环模型下三维多极化天线MIMO信道建模[J].电视技术,2013,37(23):179-182.
[2]周围,吴敏子.基于分组的 ML-SIC的 MIMO联合检测算法[J].电视技术,2013,37(15):16-128.
[3]GAN Y H,LING C.Complex lattice reduction algorithm for low-complexity full diversity MIMO detection[C].IEEE Transactions on signal processing,2009,57(7):2701-2710.
[4]WESEL R D,CIOFFI J M.Precoding and the MMSE-DFE. Signals[J].Systems and Computers,2013(2):1144-1148.
[5]MA G D,WU M Q,XU C X,et al.Lattice-reductionaided Tomlinson-Harashima precoding based on MMSE criteria in multi-user MIMO downlink system[J].Communication Technology and Application,2011,12:98-102.
[6]WINDPASSINGER C,FISCHER R,HUBER J B.Lattice-reduction-aided broadcast precoding[J].Communications[J]. IEEE Transactions,2004,52(12):2057-2060.
[7]DAMEN M O,CAIRE G.On Maximum likelihood detection and the Search for the closest Lattice Point[J].IEEE Transactions on information theory,2003,49(10):2389-2402.
[8]刘向辉,韩文报,权建校.基于遗传策略的格基约化算法[J].电子与信息学报,2013,35(8):1940-1945.
[9]方旺盛,曾苑,岳崇伦.基于粒子群优化和小波变换的视频水印算法[J].电视技术,2013,37(1):122-125.
[10]张庆荣,王刚.LR算法在MIMO_LAS_CDMA系统中的应用[J].吉林大学学报:信息科学版,2006(1):12-17.
[11]赵晓群,章惜珍,屈非,等.MIMO系统LLL格基约减检测技术研究[J].大连民族学院学报,2011,13(1):19-23.
[12]ARBERO Lg,RATNARAJAH T,COWAN C.A comparison of complex lattice reduction algorithms for MIMO detection[J]. IEEE International conferences on Acoustics,2008,4(1):2705-2708.
[13]ZHANG W,QIAO S Z,WEI Y M.HKZ and Minkowski reduction algorithms for lattice-reduction-aided MIMO detection[J].Signal Processing,IEEE,2012,60(11):5963-5976.

图4 算法运算时间仿真图
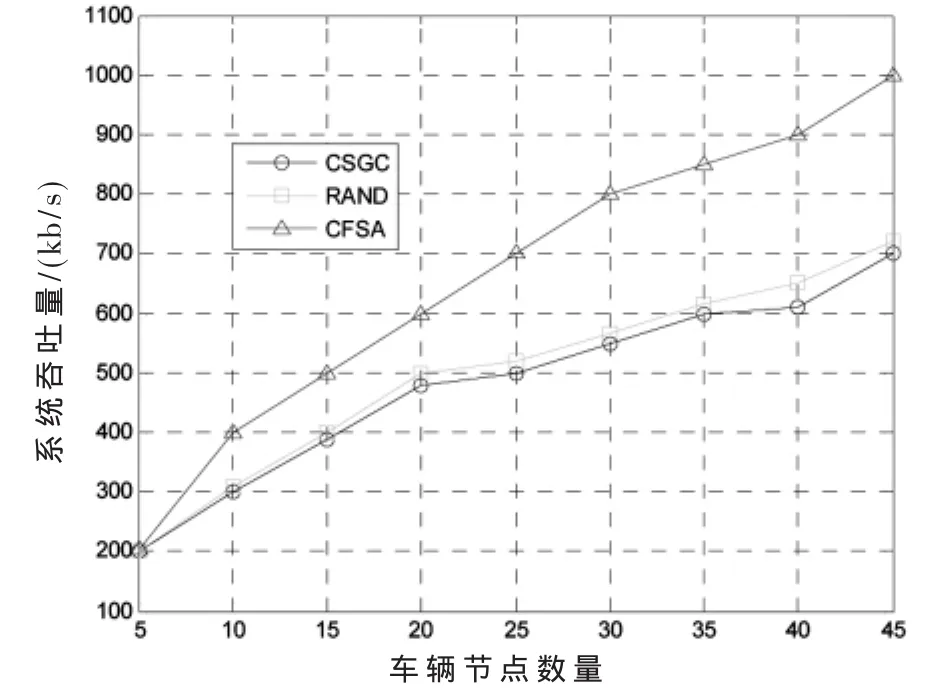
图5 系统最大化吞吐量
参考文献
[1]罗涛,王昊.车载无线通信网络及其应用[J].中兴通讯技术,2011,17(3):1-7.
[2]KAKARLA J,SATHYA S S.A survey and qualitative analysis of multi-channel MAC protocols for VANET[J].International Journal of Computer Applications,2012,38(6):38-42.
[3]SUBRAMANIAN A P,GUPTA H,DAS S.Minimum interference channel assignment in multi-radio wireless mesh netwoks[EB/OL].(2008-06-18)[2013-06-12].http://www.cs. sunysb.edu/~hgupta/ps/channel.pdf.
[4]Zheng Haitao,Peng Chunyi.Utilization and fairness in opportunistic spectrum access[C].IEEE International Conference on Communications(ICC),2006,11:555-576.
[5]WANG W,LIU X.List-Coloring based channel allocation for open-spectrum wireless networks[C].IEEE Communications Society Press,2005:690-694.
[6]ZHENG H,PENG C.Collaboration and fairness in oppor tunistic spectrum access[C].IEEE Communications Society Press,2005:3132-3136.
[7]陈劼,李少谦,廖楚林.认知无线电网络中基于需求的频谱资源分配算法研究[J].计算机应用,2008,28(9):2188-2191.
(收稿日期:2014-08-02)
作者简介:
孙智乐(1990-),男,硕士研究生,主要研究方向:移动自组网及其算法。
李德敏(1963-),男,博导,教授,主要研究方向:移动计算理论及其应用。
陶冰(1991-),男,硕士研究生,主要研究方向:移动自组网及其路由算法。
Preceding technique for MIMO based on PSO-LR
Zhang Chunkai
(Department of Computer Applications,Jiangsu Food and Pharmaceutical Science College,Huai′an 223003,China)
In order to obtain better communication results and reduce error rate of multi input multi output wireless system,a novel preceding technique for multi input multi output based on particle swarm algorithm optimizing lattice reduction algorithm was proposed to solve the problem of lattice reduction algorithm(PSO-LR).In our approach,the initial lattice was scrambled to get a set of lattice,and taken as initial particle,and then the optimal lattice was obtained by particle swarm optimization algorithm.Finally,the performance of the algorithm was tested by simulation experiments.The results show that compared with other methods,our method can effectively reduce the error rate of multi input multi output communication.
multi input multi output;pre-coding;genetic algorithm;lattice reduction
TP391
:A
:0258-7998(2015)03-0093-04
10.16157/j.issn.0258-7998.2015.03.024
2014-08-23)
张春凯(1976-),男,硕士,副教授,主要研究方向:计算机网络、网络安全。

