防发散无迹卡尔曼滤波自适应网格交互式多模型算法*

张园，董受全，钟志通，刘淑波，初俊博

（海军大连舰艇学院，辽宁大连116018）

防发散无迹卡尔曼滤波自适应网格交互式多模型算法*

张园，董受全，钟志通，刘淑波，初俊博

（海军大连舰艇学院，辽宁大连116018）

针对非线性观测条件下的机动目标跟踪问题，基于机动目标的协同转弯模型，采用防发散无迹卡尔曼滤波方法和自适应网格的模型集自适应策略，研究了一种变结构交互式多模型算法。对二维机动目标跟踪的仿真结果表明，该算法与相应的固定结构交互式多模型算法相比，可以解决固定结构多模型算法存在的问题，有效提高多模型算法的精度和费效比，缩短计算时间，且适合工程应用。

无迹卡尔曼滤波（UKF），自适应网格（AG），交互式多模型（IMM），机动目标跟踪，变结构多模型（VSMM）

0 引言

目标跟踪是军事和民用领域中的一个基本问题。在机动目标跟踪中，目标的动态模型通常是在笛卡尔坐标系下进行建模，而雷达量测都是以极坐标形式表示，包括目标与雷达的距离、方位角和俯仰角，这样目标跟踪就变为一个非线性估计问题［1］。在处理非线性估计问题中应用最广泛的方法是扩展卡尔滤波器（Extented Kalman Filtering，EKF），这种方法存在线性化误差大、雅可比矩阵难于计算等明显的缺陷，在高度非线性情况下，滤波不稳定，误差会很大甚至发散。针对这些问题，近年来，出现了用于非线性系统、基于无迹变换（Unscented Transform，UT）滤波新思想的无迹卡尔曼滤波器（Unscented Kalman Filtering，UKF），可以有效改善滤波效果。由于采用无迹变换对非线性概率密度分布进行近似，具有不需要求导、估计精度高等优点，已经取代EKF成为非线性滤波的主要算法，并被应用于导航定位、信号处理、目标跟踪等领域中。

机动目标跟踪算法可以分为单模型算法和多模型算法两种。目标在机动时，其运动特征（速度、加速度、运动方向等）时常变化，使用单一模型很难准确描述目标的运动状态，因此，出现同时使用多个模型来描述机动目标运动状态的算法。多模型算法首先由Magill提出［2］，其发展经历了3代［3-4］。第1代多模型算法的特点是模型个数固定，各滤波器单独运行，最后对其输出进行融合。第2代多模型算法，以交互式多模型（Interacting Multiple Model，IMM）算法为典型代表，仍然使用固定的模型个数，但各个模型之间存在交互［5］。前两代均属于固定结构多模型（Fixed Structure Multiple Model，FSMM）算法。然而在现实中，目标机动模式仅用少数几个模型描述很可能是不够的，多维系统更为如此。但是增加模型数目，不仅会增加计算量而且并非一定能够改善跟踪性能，过于细化的模型空间也可能破坏贝叶斯推理所要求的模型间独立的要求。基于FSMM算法存在的上述问题，出现了第3代多模型算法：具有可变模型集的变结构多模型（Variable Structure Multiple Model，VSMM）算法［6-7］。VSMM算法有3种基于图论的实用方法［8］：活跃的有向图（Adaptive Digraph，AD），有向图切换（Digraph Switching，DS）和自适应网格（Adaptive Grid，AG）方法。

针对非线性观测条件下的机动目标跟踪问题，本文借鉴线性滤波中卡尔曼滤波器的S修正防发散思想［9］，对基本的无迹卡尔曼滤波算法进行防发散改进，得到一种防发散无迹卡尔曼滤波器（ADUKF）。然后采用这种防发散无迹卡尔曼滤波方法，结合自适应网格（AG）的模型集自适应策略，研究了一种变结构交互式多模型算法，即：基于防发散无迹卡尔曼滤波的自适应网格交互式多模型（Adaptive Grid Interacting Multiple Model Algorithm Based on Anti-divergent Unscented Kalman Filtering，ADUKF-AGIMM）算法。最后，应用该算法对二维仿真环境下的机动目标进行跟踪，证明了算法的有效性和优越性。

1 数学模型

系统的状态方程和观测方程如式（1）和式（2）所示。

2 ADUKF-AGIMM算法设计

2.1 算法步骤

ADUKF-AGIMM算法的计算步骤有如下5步：

第1步，输入交互。

假设子模型集包含r个模型。

计算混合概率：

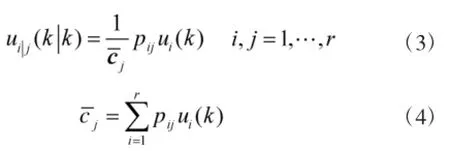
状态估计初值的输入交互：

第2步，防发散无迹滤波。

借鉴线性滤波中卡尔曼滤波器的S修正防发散思想［9］，对基本的无迹卡尔曼滤波算法进行防发散改进，以减少估计误差。

对j=1，…，r。

式中i=1，2，…，2n，其中n为状态向量维数；λ=α2（n+k）-n，α决定了σ点的散布程度，通常取一较小正值，如0.01；k这里取0。

（2）计算西格马点通过状态方程的传播。

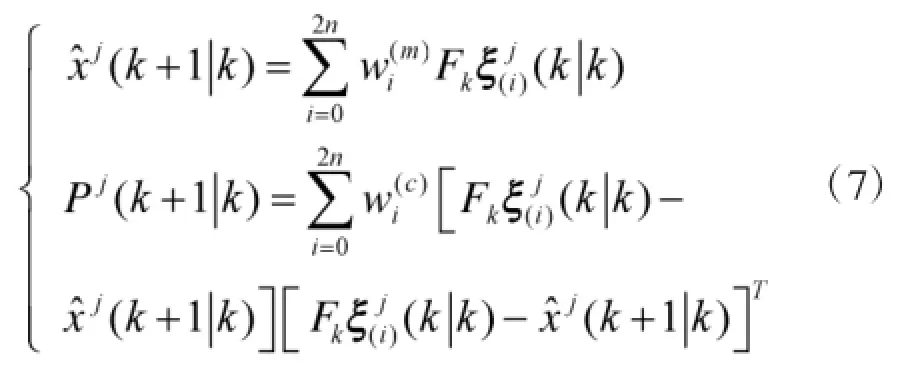
式中，

这里，β=2。

（3）防发散修正。

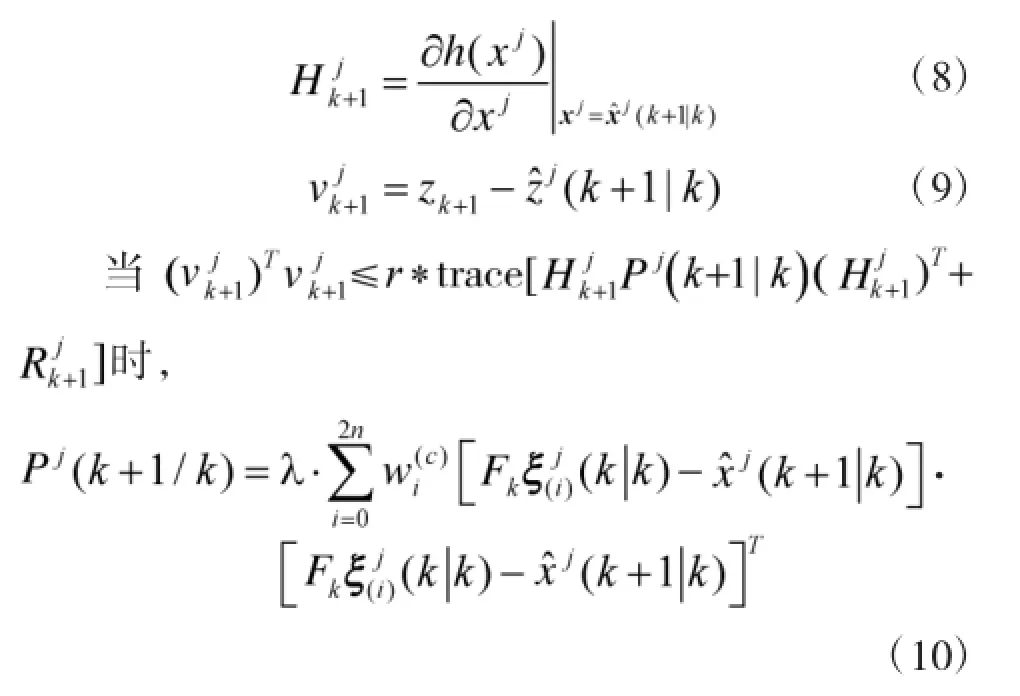
其中，λ为一标量常数，可根据经验选取，一般取λ>1。

（4）计算西格马点通过量测方程的传播。

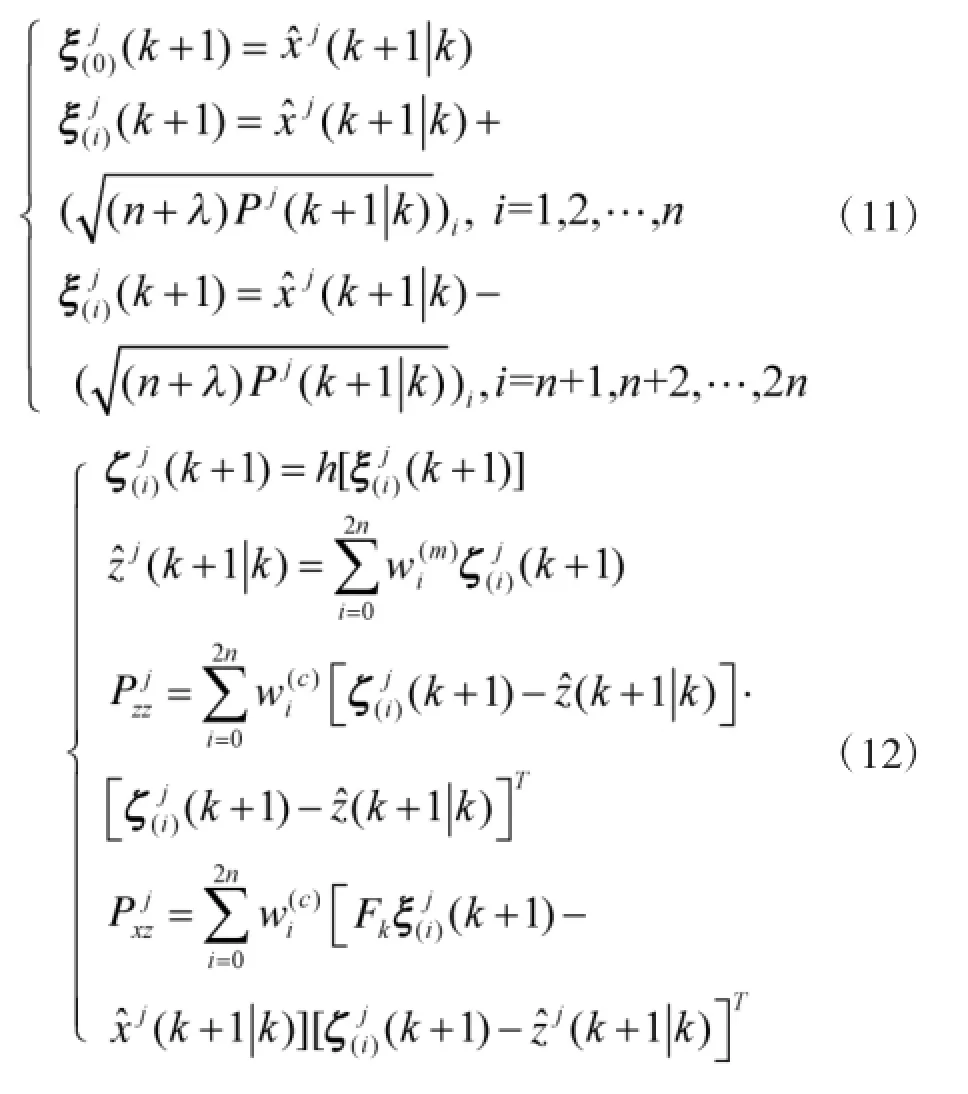
（5）在新的量测值zk+1到达后进行滤波更新。

第3步，模型概率更新。

似然函数：

模型概率更新：

第4步，输出交互。

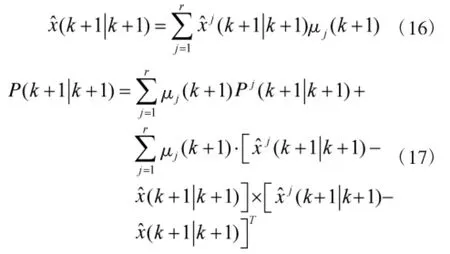
第5步，模型集自适应网格调整。具体算法见2.2。

2.2 自适应网格调整算法

基于协同转弯机动模型，以转弯速率的连续间隔作为模型集的网格，自适应网格调整算法设计如下。假设机动目标当前转弯速率是在连续范围内，但真实值未知。构建一个具有时变的3个模型的IMM算法，k时刻模型集为。

第1步，网格中心调整。

网格中心调整如式（18）所示。

第2步，网格距离调整。

网格距离调整分为无跳变、向左跳变、向右跳变3种情况。

2.2.1 无跳变

2.2.2 向左跳变

式中，t2为重要模型概率门限。

2.2.3 向右跳变

3 仿真结果与分析

为了验证ADUKF-AGIMM算法性能，将其与IMM3和IMM7进行比较，这里IMMn（n=3，7）表示IMM算法中模型集分别由3个和7个固定模型组成。滤波算法采用基本UKF算法。

假设目标在x-y平面运动，仿真场景如下［10-11］：初始位置为（3 000 m，-1 000 m），初始速度为600 m/s（与x轴的夹角为35°），仿真时间为200 s。仿真轨迹共5段，目标在0≤t≤30 s内做匀速直线运动，在31 s≤t≤90 s内做角速度为ω=-0.02 rad/s的匀速转弯运动，在141 s≤t≤170 s内做匀速直线运动，在期间做角速度为ω=0.1 rad/s的匀速转弯运动，在171 s≤t≤200 s期间做匀速直线运动。

仿真时，IMM3使用的模型集为{ω=-6°/s，ω=0 °/s，ω=6°/s}，IMM7使用的模型集为{ω=-6°/s，ω=-4 °/s，ω=-2°/s，ω=0°/s，ω=2°/s，ω=4°/s，ω=6°/s}。

设IMM3算法中IMM的模型转移概率均为p=［0.7，0.2，0.1；0.2，0.7，0.1；0.1，0.2，0.7］。IMM7算法中IMM的模型转移概率为{pij}ni，j=1。pii=0.9，i=1，7；pi－i=0.8，i=2，6；pii-1=0.1，i=2，…，7；pii+1=0.1，i=1，…，6。设量测噪声为零均值的高斯噪声，其标准差为diag［150 0.3］。

ADUKF-AGIMM算法中每个时刻的模型集由3个模型组成，模型集中各模型交互概率同IMM3算法。不可能模型概率门限取为t1=0.05，重要模型概率门限取为t2=0.92，最小网格间隔取为δω=0.5°。

取采样周期为T=1 s，分别对各算法进行100次Monte Carlo仿真，IMM3和ADUKF-AGIMM算法的位置均方根误差（Root Mean Squared Error，RMSE）和速度RMSE的仿真曲线分别如图1～图4所示。ADUKF-AGIMM、IMM3和IMM7算法的位置RMSE和速度RMSE的仿真结果如表1所示，3种算法的平均计算时间如表2所示。

图1 x方向位置RMSE曲线

图2 y方向位置RMSE曲线

图3 x方向速度RMSE曲线

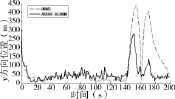
图4 y方向速度RMSE曲线

表1 100次蒙特卡罗仿真结果

表2 100次蒙特卡罗仿真平均计算时间

由图1～图4和表1、表2可以看出，

（1）ADUKF-AGIMM和IMM3算法同样使用了由3个模型组成的模型集，但是ADUKF-AGIMM算法的跟踪精度相对于IMM3算法有了明显提高，并且目标的机动性愈强，ADUKF-AGIMM算法的优势愈明显；

（2）ADUKF-AGIMM和IMM7算法跟踪精度相当（前者比后者跟踪精度略有提高），但是ADUKF-AGIMM算法使用了由3个模型组成的模型集，IMM7算法使用了由7个模型组成的模型集，ADUKF-AGIMM算法比IMM7算法的计算复杂度和计算时间大幅降低，其平均计算时间只有IMM7算法的45%。

综上，相对于FSMM算法，当使用相同的模型数时，ADUKF-AGIMM算法能大幅度提高跟踪精度，而FSMM算法要达到ADUKF-AGIMM算法的跟踪精度必须使用2倍以上的模型数，相应的计算时间增加了1.2倍。总之，ADUKF-AGIMM算法所需的模型少，计算简单，计算时间短，提高了多模型算法的费效比。

4 结论

本文研究了一种基于防发散无迹卡尔曼滤波和自适应网格的机动目标跟踪变结构交互多模型算法。该算法解决了FSMM算法存在的问题：当模型集中的模型个数较少时，由于模型集不能完全覆盖目标的各种机动模式而引起精度下降；当模型集中的模型个数较多时，会使计算量激增，并且带来各模型间不必要的竞争，从而降低算法的费效比。蒙特卡罗仿真结果表明，ADUKF-AGIMM算法能够大幅减少模型数量，缩短计算时间，却能更好地匹配目标运动规律，提高了跟踪精度（目标的机动性愈强，优势愈明显），且适合于工程实用。

［1］朱安福，景占荣，高田，等.基于UKF的交互多模型算法［J］.系统仿真学报，2009，21（3）:655-657.

［2］尹海斌.雷达机动目标跟踪滤波算法的研究［D］.大连：大连海事大学，2008.

［3］张敏.基于粒子滤波的可变结构多模型估计［D］.合肥：中国科学技术大学，2010.

［4］刘高峰，顾雪峰，王华楠.强机动目标跟踪的两种MM算法设计与比较［J］.系统仿真学报，2009，21（4）:965-968.

［5］Gao L，Xing J P，Ma Z L，et al.Improved IMM Algorithm for Nonlinear Maneuvering Target Tracking［C］//2012 International Workshop on Information and Electronics Engineering，2012.

［6］黄翔宇，彭冬亮.基于无味有向图切换的机动目标跟踪VSMM算法［J］.光电工程，2011，37（12）:30-34.

［7］雷世文，吴慈伶，孙伟.一种基于VSMM的自适应高机动目标跟踪方法［J］.现代雷达，2010，32（6）:54-58.

［8］Li X R，Jilkov V P.A Survey of Maneuvering Target Tracking–Part V:Multiple-Model Methods［C］//IEEE Transactions onAerospaceandElectronicSystems，2005，41（4）: 1297-1298.

［9］张园.卡尔曼滤波及其军事应用［M］.大连：海军大连舰艇学院出版社，2010.

［10］郭云飞，张幸，林岳松.基于DS_VSMM的声网络低空机动目标跟踪［J］.光电工程，2011，38（8）:1-7.

［11］张安清，王为颂，郑润高，等.舰载雷达目标跟踪的非线性滤波仿真［J］.舰船科学技术，2011，33（4）:98-101.

Adaptive Grid Interacting Multiple Model Algorithm Based on Anti-divergent UKF

ZHANG Yuan，DONG Shou-quan，LIU Shu-bo，CHU Jun-bo
（Dalian Naval Academy，Dalian 116018，China）

Devoted to the problem of maneuvering target tracking under nonlinear observation，an Anti-Divergent Unscented Kalman Filtering（ADUKF）is developed in this paper，which uses the ideas for reference of S-amended anti-divergent method for Kalman filter in linear filtering and improves the performance of unscented Kalman filtering algorithm.Based on the Coordinated Turn（CT）models，a Variable Structure Multiple Model（VSMM）algorithm named adaptive grid interacting multiple model algorithm based on Anti-Divergent Unscented Kalman Filtering（ADUKF-AGIMM）is researched with the anti-divergentunscented Kalman filtering method mentioned above and adaptive strategy of Adaptive Grid（AG）.Simulation results show that this algorithm can solve the problems of Fixed Structure Multiple Model（FSMM）algorithm，effectively improve the accuracy and cost-efficiency ratio of the multiple model algorithm，reduce the computation time in contrast to corresponding fixed structure algorithm，and is suitable for engineering applications.

Unscented Kalman Filter（UKF），Adaptive Grid（AG），Interacting Multiple Model（IMM），maneuvering target tracking，Variable Structure Multiple Model（VSMM）

TP713

A

1002-0640（2015）02-0040-05

2013-12-14

2014-01-17

国家自然科学基金（61074053，61374114）；交通部应用基础基金资助项目（2011-329-225-390）

张园（1972-），女，山东青岛人，副教授，博士。研究方向：机动目标跟踪、智能控制。