按最小传动角设计曲柄摇杆机构的图解方法*



按最小传动角设计曲柄摇杆机构的图解方法*

刘争利

(南京电子技术研究所，江苏 南京210039)

摘要：根据曲柄摇杆机构设计的图解方法和最小传动角的要求，借助Solidworks中的约束功能使绘制出的机构草图处于完全定义状态，快速定位出曲柄转动中心的位置，从而求出其余杆件的长度。该方法操作简单并且设计精度高，在机械设计方面有较好的应用价值。

关键词：曲柄摇杆机构；最小传动角；约束；图解法；Solidworks

0引言

曲柄摇杆机构具有结构简单、制造容易、工作可靠的特点，在众多机械中得到了广泛的应用。在目前的设计方法中，传统的图解法简单易行，尤其在阐述原理和构型分析等方面发挥出无可替代的作用，但该方法最大的缺点在于必须用反复试凑的手段来寻求符合传动角要求的机构尺寸，因此设计精度低；解析法借助计算机以及数值计算等方法，设计精度高，能满足工程实际需要，但计算公式多，过程复杂，需编制程序求解非线性方程组，从而影响了设计效率[1-3]。

因此，若能发挥图解法和解析法各自的优势，方便快捷地得到精确的机构设计结果是工程人员所期望的最终目标。笔者将介绍借助Solidworks的约束功能去完成以最小传动角设计曲柄摇杆机构的图解方法，从而实现机构图解法的精确设计。

1传动角对机构的影响和其最小值的确定

考虑到度量方便，通常用压力角α的余角γ(即曲柄AB通过连杆BC作用在摇杆CD上的力F与F沿摇杆方向的分力Fn所夹的锐角)来判断机构传力的性能，γ称为传动角，由图1可知，γ越大，则机构的传动性能就越强。在机构运动过程中，传动角的大小是变化的，为了保证机构具有良好的传动性能，必须对最小传动角γmin提出要求：对于一般的机构通常取γmin≥40°，而对于高速和大功率的传动机械，应使γmin≥50°。

如果用δ表示连杆BC与摇杆CD的夹角，当δ为锐角时，则γ=δ；当δ为钝角时，则γ=180°-δ。δ随曲柄AB与机架AD之间的转角φ的变化而变化。

由图1可推出：

(1)

由公式(1)可知，在δ=δmin或δ=δmax时，该机构出现最小传动角γmin，即：

(2)

(3)

故可得：

γmin={δmin(锐角)，δmax(锐角)，[180°-δmin(钝角)]，[180°-δmax(钝角)]}

(4)

图1　曲柄摇杆机构的传动角

由文献[4]可知，对于图1所示的所有曲柄摇杆机构(曲柄转动中心A和摇杆摆动中心D位于C′C″连线同侧)，其最小传动角γmin在φ=0°的位置上出现，即γmin=δmin；对于曲柄转动中心A和摇杆摆动中心D位于C′C″连线异侧的所有曲柄摇杆机构，其最小传动角γmin在φ=180°的位置上出现，即γmin=δmax。

2曲柄摇杆机构的图解设计

具有急回特性的曲柄摇杆机构，其设计的已知条件为：摇杆长度CD和其摆角ψ以及行程速比系数K。多数参考资料的图解设计过程如下。

首先，计算出极位夹角θ，即：

(5)

其次，任选一点D作为固定铰链，如图2所示，并以此点为顶点作等腰三角形DC2C1。使两腰之长等于摇杆长度CD，∠C1DC2=ψ。然后过C1点作C1M⊥C1C2，再过C2点作∠C1C2N=90°-θ，线段C1M和C2N的交点为P。

图2　图解法设计曲柄摇杆机构

最后，以线段C2P为直径作圆，则此圆周上任一点与C1，C2连线所夹之角度均为θ。曲柄转动中心A应在圆弧C1PF或C2G上任取，不能在FG劣弧上取，否则机构将不能满足运动的连续性[5]。由图2可知，曲柄AB与连杆BC重叠共线和拉直共线的两个位置为AC1和AC2，则：

AC1=B1C1-AB1

(6)

AC2=B2C2+AB2

(7)

由式(6)和式(7)两式可解得曲柄AB长度和连杆BC长度

AB=(AC2-AC1)/2=EC2/2

BC=AC2-AB2

线段EC2可由以A为圆心、AC1为半径作圆弧与AC2的交点E来求得，也可以认为线段EC2的长度就是曲柄AB长度的两倍，即：

EC2=2×AB

(8)

由图2可知，当曲柄转动中心A点取在不同的位置时，满足上述设计条件的曲柄摇杆机构会有无穷多个，同时所对应的最小传动角也不相同。因此，设计时若能给出其他附加条件(如最小传动角的要求)，则能确定出曲柄转动中心A的位置。

3约束对草图自由度的限制

在Solidworks软件中，草图一般是指在面上的二维几何图形，是特征造型的基础；约束是对草图中的图元形状、大小和位置所施加的各种控制条件，这些控制条件可以在草图绘制过程中由系统自动添加或由设计者自行添加。约束可分为几何约束和尺寸约束两大类[6]，例如，通过几何约束可定义草图中某一图元的方向(如固定、水平、竖直)或某两个图元间的关系(如共线、垂直、平行、相等、同心、重合、相切等)；通过尺寸约束(包括线性尺寸、角度尺寸和圆弧尺寸等)可确定草图中图元的大小和位置。

定义1 草图自由度是指构成草图中的各个基本图元自由程度的总和。用Sf代表草图自由度，则：

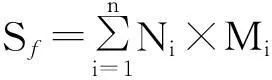
(9)

式中：Ni是第i种基本图元的数量；Mi是第i种基本图元的自由程度；n为基本图元的种类。

定义2 约束度是指添加约束后，对草图自由度的限制。用Cf表示约束度，则：

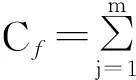
(10)

式中：Aj是第j种约束的数量；Bj是第j种约束所限制自由的程度；m为约束的种类。

在上述定义中，关于基本图元的种类与自由程度、不同约束所限制自由的程度这两方面的说明，可以参考文献[7]，本文不再详述。

当SfCf时，表示草图欠定义，其实体可能在某个方向进行移动或转动，欠定义的草图实体颜色系统显示为蓝色，如图2所示的线段AD、AC2和B1C1等；当Sf=Cf时，代表草图完全定义，其实体的位置、形状和大小是唯一的，完全定义的草图实体颜色系统显示为黑色，如图2所示的线段C1D和C2D等。

4按最小传动角图解设计的步骤

由以上分析可知，在Solidworks环境下若能够使绘制出的曲柄摇杆机构草图处于完全定义状态，那么按最小传动角的要求就能确定出曲柄转动中心的具体位置[8]。

图解设计的过程如图3所示，首先，根据工程实际设置尺寸的精度；再依据已知条件(摇杆长度和其摆角ψ以及行程速比系数K)，绘制出一个大致的机构草图，其中图元间的几何约束是系统根据图元间的位置自动判断并添加的，以绿色图标标识，如图2所示；然后添加必要的几何约束(如连杆在不同位置时的杆长关系，图2中的线段EC2与曲柄AB的长度关系)和尺寸约束(按最小传动角的附加条件设置连杆和摇杆之间的角度)使草图成为完全定义状态；最后，根据确定出的曲柄转动中心位置，测量出其余的杆件长度。

图3　图解设计流程

5应用实例

设计一曲柄摇杆机构，已知摇杆的长度LCD=100 mm，摇杆摆角ψ=32°，行程速比系数K=1. 25，最小传动角γmin=40°，试确定出曲柄LAB、连杆LBC和机架LAD的尺寸。

(1) 设置尺寸精度

由于已知条件中没有明确的精度要求，考虑到有不可避免的制造误差，所以在SolidWorks中将尺寸精度设置为小数点后3位，这对于尺寸单位为毫米来讲，设计出的结果完全满足于工程实际要求。若有明确的精度要求，则按需要设置即可，精度最高可设置为小数点后8位。

(2) 绘制草图

通过公式(5)计算出极位夹角θ=20°，首先按图解法步骤大致绘出如图2所示的曲柄摇杆机构草图，在圆弧C1PF上任取一点为A点，连接AD；然后以图4所示的A点为圆心，以适当半径为大小做圆①交AD连线于B点，连接C1A并延长交圆①于B1点，连接C2A交圆①于B2点；接着自B点作连线BC交C1C2劣弧于C点(此劣弧是以D为圆心，以摇杆的长度LCD为半径所得的圆弧)，连接CD；最后再以A点为圆心，以AC1为半径画弧交AC2于E点，以C2E为直径作圆②。

(3) 添加约束

在上述草图绘制过程中，所有草图实体的几何关系是系统自动添加的，我们无需再进行设置。现在需要为连杆在两个不同位置处的长度设置“相等”的几何约束，即线段BC和线段B1C1；根据式(8)所描述的含义，为图4中的圆①和圆②添加“相等”的几何约束。根据最小传动角的要求，为线段BC和线段CD添加“角度”约束关系，即通过“标注尺寸”命令来实现，使∠BCD=40°，此时图中的所有线条颜色全部成为黑色，表明草图处于完全定义状态，即A点的位置唯一确定。

(4) 测量尺寸

执行“标注尺寸”的命令，选择线段B1C1，此时系统会提示“增加这个尺寸将导致草图过定义”的提示，这表明尺寸已定义，可将尺寸设为从动，标出的尺寸会以灰度状态显示出来，如图4所示。这时标注尺寸的意义只相当于测量出设计结果的功能，以同样的方式，将线段AD和AB1的长度测量出来。

设计结果为：曲柄长度LAB=22.651 mm，连杆长度LBC=94.243 mm，机架长度LAD=89.048 mm。

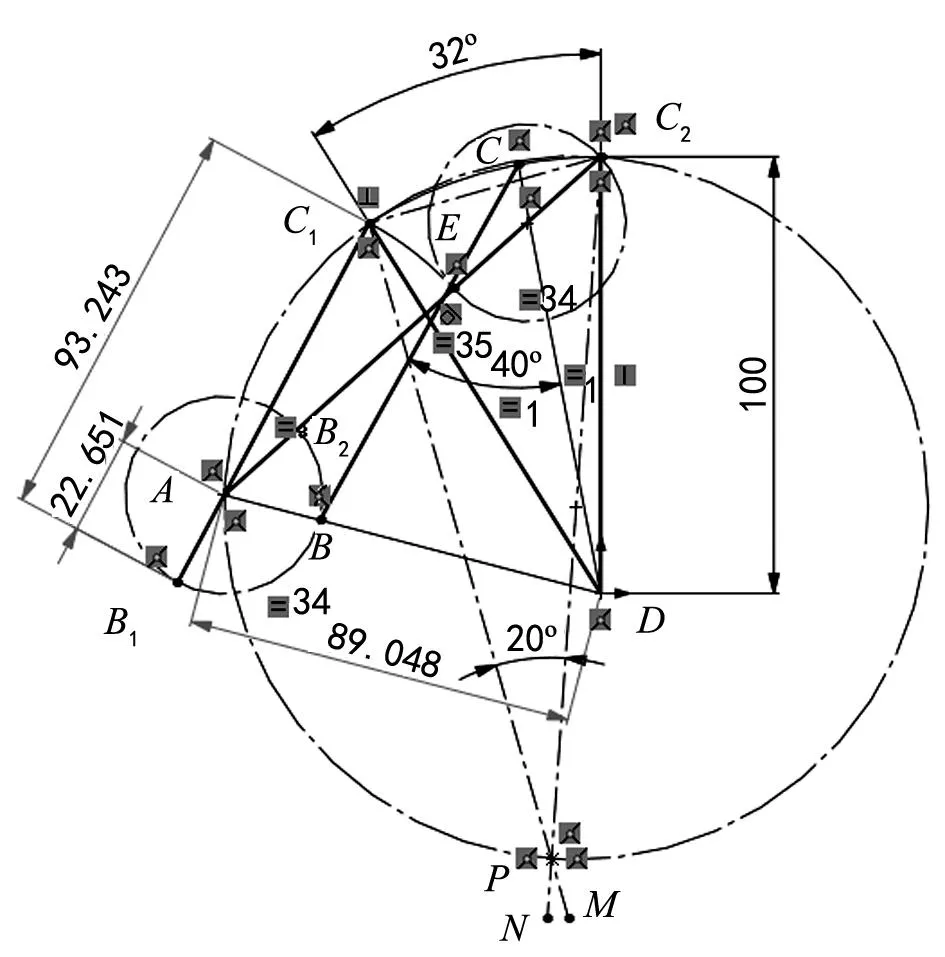
图4曲柄摇杆机构的设计结果

5结论

由于该方法不涉及机构设计的数学建模和计算编程，所以易被普通机械设计者所接受，另外也可作为专业设计研究人员用于与解析法相互验证的一种相辅相成的有效手段[9]。总而言之，使用SolidWorks进行曲柄摇杆机构的图解法设计，既有传统图解法简便直观的特点，又有解析法精确程度高的优点，这不仅在设计效率方面有了很大的提高，同时在设计思想和方法上有了新的飞跃，值得大力推广和应用。

参考文献：

[1]张静,王占英,刘春东,等. 按最小传动角设计曲柄摇杆机构的解析方法[J].机械设计,2008(10):64.

[2]孟维云.鹿晓阳.曲柄摇杆机构的综合优化设计[J].机械研究与应用,2008(6):87-89.

[3]王勇. 宋德朝.基于MATLAB/Simulink的四杆机构连杆点轨迹仿真, 机械研究与应用,2007(3):98-100.

[4]李均益. 也谈判定曲柄摇杆机构γmin三命题的证明[J].机械设计,1996(6):37-38.

[5]申永胜. 机械原理教程[M ].北京:清华大学出版社,2005.

[6]湛迪强. Solidworks2008宝典[M].北京:电子工业出版社,2008.

[7]饶刚. Solidworks约束与草图自由度的关系[J].湖北工业大学学报,2005(6):40.

[8]杨晓龙,史丽晨.曲柄摇杆机构图解法的参数化设计[J].煤矿机械,2015(2):55-57.

[9]陈辽军,郑晓虎,张强. 利用SolidWorks约束功能实现机构图解法的参数化设计[J].轻工机械,2004(3):59.

Graphic Method for Designing Crank-Rocker Mechanism According to Minimum Transmission Angle

LIU Zheng-li

(NanjingResearchInstituteofElectronicsTechnology,NanjingJiangsu210039,China)

Abstract:According to the graphic method of crank-rocker mechanism design and the requires of minimum transmission angle, the sketch is drawed out in fully defined situation by using the constraint functions of Solidworks, thus the position of rotation center of the crank could be quickly located so as to obtain the length of the rest rods. This method is simple and has high design accuracy, and could possesse a good application value in mechanism design.

Key words:crank-rocker mechanism; minimum transmission angle; constraints; graphic method; Solidworks

中图分类号:TH123

文献标志码：A

文章编号：1007-4414(2015)03-0157-003

作者简介：刘争利(1975-)，男，陕西西安人，工程师，硕士，研究方向：天线结构设计。

*收稿日期：2015-05-27
基金资助：国家自然科学基金重大项目(编号：51490664)