基于改进傅里叶算法的工频电气量的提取方法

季　亮, 姜恩宇

(上海电力学院 电气工程学院, 上海　200090)



基于改进傅里叶算法的工频电气量的提取方法

季亮, 姜恩宇

(上海电力学院 电气工程学院, 上海200090)

摘要:提出了一种能滤除衰减直流分量影响的改进傅里叶算法.该算法利用正弦函数相隔半个周期的采样数据相加为零的原理,得到一个关于衰减直流分量的数学表达式,进而计算衰减直流分量的数值.仿真结果显示,该算法具有较好的精确性,其输出结果能够准确反应短路电流中的工频值.

关键词：傅里叶算法; 工频量; 微机保护; 衰减直流分量

现代电力系统是一个巨大的统一的整体,系统中的装置以及所接的用电设备都是开放性设备,受周围环境的影响而发生故障的可能性很大.而继电保护装置是电力系统中不可缺少的一部分.通过继电保护装置的正确动作,可在系统发生故障时迅速切断电源,保护电力设备不被损坏.现代计算机技术影响着电力系统继电保护技术的发展.[1-2]现代的保护装置大部分由微机保护组成,微机保护中实现功能和继电保护基本任务的模块是各种各样的保护算法.[3]

文献[1]至文献[5]从电压电流为纯正弦变化的情况出发,提出了在半个周期内找最大值的算法、导数算法、采样值积的算法和解方程组的算法等.由于这些算法都是基于被采样的电压和电流是纯正弦变化的,而实际上在电力系统发生故障时,往往是在基波的基础上叠加有衰减的非周期分量和各种高频分量,因此计算机保护装置对输入的电流电压信号必须进行预处理,尽可能地过滤掉非周期分量和高频分量,否则将会出现较大误差.

针对上述情况,文献[6]至文献[14]假设电流是由非周期分量、基频和倍频分量所组成,提出了一些基于较复杂的数学模型的算法.傅里叶算法由两个全周波的正弦滤波器和余弦滤波器构成,算法的数据窗为每周波的全部采样点,可以很好地滤除信号中的恒定直流分量和高次谐波分量,并且计算快速、简单,是电力系统使用最多的算法,但算法本身不能滤除衰减的非周期分量.在超高压电力系统中,为了克服随机噪声的影响,除了采用较完善的滤波措施外,还提出了一些减少误差的算法.例如对计算结果采取平滑措施,[15]采用最小二乘曲线拟合算法[16-17]等.

本文介绍了一种改进的傅里叶算法,可以大幅减少衰减直流分量对传统傅里叶算法的影响.该算法利用正弦函数相隔半个周期的采样值相加为零的原理,得到计算衰减直流分量的数学表达式,并计算出衰减直流分量的数值,最终可在算法的输出结果中消去衰减直流分量.

1傅里叶算法的基本原理

傅里叶算法的基本思想源于傅里叶级数.假设被采样的模拟量信号是一个周期性的时间函数,可以是正弦函数,也可以是含有多种谐波成分的非正弦函数,根据傅氏级数的概念,可将此周期函数分解为恒定的直流分量和各种高次谐波分量.

以电流为例,假设有一原始信号为：

式中:n——谐波次数,n=0,1,2,3,…;

an,bn——各次谐波的余弦项和正弦项的振幅,即经傅氏变换后所得向量的实部和虚部.

根据傅氏级数的原理,可以求出an和bn分别为:

(2)

(3)

据an和bn可计算出n次谐波的幅值和相角分别为:

(4)

(5)

2改进的傅里叶算法

任何电力系统中的故障或扰动都会产生衰减直流分量,其衰减率取决于系统的时间常数,即X/R(电感与电阻的比值).X/R的值越大,直流分量就衰减得越慢.作为一种非周期信号,衰减直流分量具有相对较宽的频率范围,这一频率范围会影响傅里叶算法结果的精确度.

本文提出的算法以傅里叶变换为基础,首先对原始波形中的某一采样点开始的半个周期进行傅里叶变换,接着在与此点相隔半个周期的采样点再进行一次傅里叶变换.两次变换所得的结果中,既有衰减直流分量的相量,也有工频50 Hz的相量.而对于50 Hz的正弦波来说,相隔半个周期进行傅里叶变换所得的两个相量大小相等,方向相反,相加为零.因此,在原始波形中,将前后相隔半个周期进行傅里叶变换所得的相量相加.由于工频分量的相量相加为零,式中只剩下了衰减直流分量的相量.

以电流为例,设输入保护装置的原始电流为:

(6)

式中:A0——衰减直流分量的幅值;

τ——衰减直流分量的时间常数;

Ak——k次谐波的幅值;

ω1——基波角速度;

θk——k次谐波的相角;

p——信号中的最高次谐波.

假设次数高于p次的谐波已经被低通滤波器消除.将原始信号输入模数转换系统,可得到离散化的采样数据为:

式中：Δt——采样间隔;

n——采样点数,即第n次采样.

对离散化的波形进行离散傅里叶变换,所得的结果为:

(8)

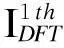
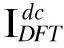
E=eΔt/π.

在某一时刻t=nΔt进行傅里叶变换,所得结果为:

(9)

式中:r——采样点数.

将求和式展开,正弦函数写成复指数相量形式,可得到：

(10)

(11)

同理,将求和式展开,正弦函数写成复指数相量形式,可得到:

(12)

式(10)和式(12)相加可以消去基波分量A1ejφ1:

(13)

式(13)所得的结果为一个复数,它可以分解为实数部分KRe和虚数部分KIm,分别为:

(14)

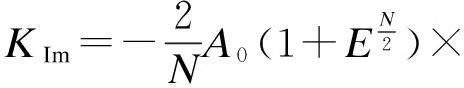
(15)

式(14)除以(15)可得到一个系数KDIV:

(16)

反解方程(16),可得E,即eΔt/τ:

(17)

由式(13)可知,衰减直流分量的相量为:

(18)

(19)

由式(19)所得的相量就是电流波形中工频量的值.

整个算法的流程如图1所示.

图1　改进算法的流程

3仿真实验及分析

运用Matlab编写特定的测试信号对改进算法进行验证,并利用电力系统仿真模型对改进算法进行验证.每个实验内容分别设置3组实验,用图形显示实验结果,并将改进算法与传统算法相比较,以验证改进算法对于消除衰减直流分量的能力.

3.1　信号1

第1个模拟电流信号由工频分量、高次谐波分量和1个衰减直流分量组成,原始信号的表达式为:

10cos(3ωt)+2cos(4ωt)

(20)

式(20)中,衰减直流分量的时间常数τ=0.1 s,ω=2πf=100π,工频为50 Hz,各谐波分量相角均为零.先后采用传统算法和改进算法对i1进行处理,得到的结果如图2所示.

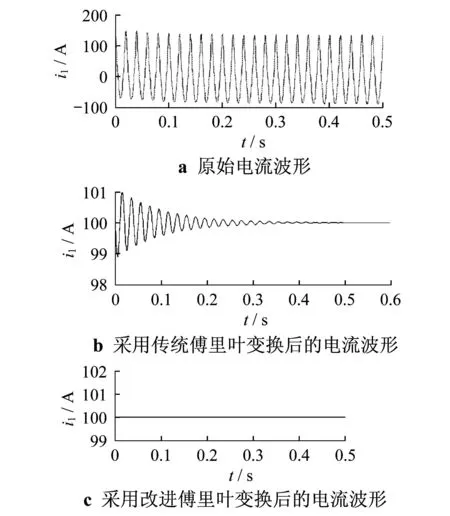
图2　不同情况下i1的仿真波形

3.2　信号2

第2个模拟电流信号由工频分量、高次谐波分量和2个衰减直流分量组成.2个衰减直流分量中,一个是模拟电力系统故障引起的非周期电流,另一个是由电流互感器产生的衰减直流分量,其时间常数τs=0.4 s,即20个工频周期.原始信号的表达式为:

(21)

式(21)中，除了τs的值外，其他值均与信号1中的相同.先后使用传统算法和改进算法对i2进行处理,得到的结果如图3所示.

图3　不同情况下i2的仿真波形

从3组对照实验可以看出，改进傅里叶算法的优势非常明显,它能很好地抑制衰减直流分量的影响.从图3中可以看出,没有经过改进的傅里叶算法不可避免地在含有衰减直流分量的情况下产生震荡,震荡的幅度在稳定值的1%左右.而改进的傅里叶算法处理电流数据的结果显示,它不经震荡地收敛于稳定值，精确地反应了测试电流的真实值.由于测试波形是已知的,因此改进算法给出的结果基本可以算是零误差.只是在第3组实验中加入干扰的情况下有微小的波动,但与传统的傅里叶算法相比，这种波动可以忽略不计.

因此,可以得出结论：改进的傅里叶算法在理论上可以完全除去衰减直流分量引起的误差,达到零误差地提取工频的电流值和电压值.

3.3　线路仿真

在Simulink中搭建一个简单的电力系统模型,如图4所示.

仿真使用了单相接地故障,故障电阻的大小为0.1 Ω,过渡电阻的大小为0.001~2 Ω,短路时间为0.3 s,仿真时间为0.8 s.保存电流数据,再分别使用传统算法和改进算法对i2进行处理,得到的结果如图5所示.

经传统傅里叶算法处理得到的工频电流的幅值，其波形必须要经过一个震荡过程才会收敛于稳定值,震荡的时间和幅值会随着衰减直流分量的改变而改变.可以大致估算出,震荡较剧烈的时间约为2 000个采样点,即0.1 s左右.由此可见,传统的傅里叶算法不能在结果中完全地滤除非周期直流量的影响.而经过改进傅里叶算法处理后得到的波形,可以明显观察到震荡的减少,并且振幅可以忽略不计.在短路发生后的很短时间内,波形就已经达到稳定值,且具有很高的精确性,可以如实地反应短路全电流中包含的工频电流值.

图4　仿真电力系统模型

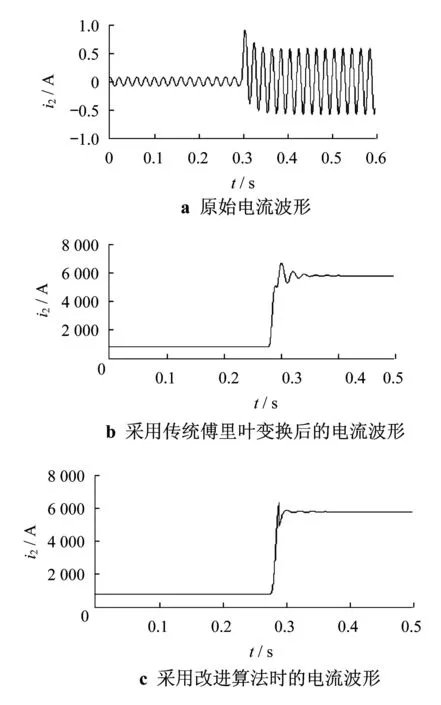
图5　采用改进算法的结果

4结语

本文通过理论验证和仿真验证,对改进算法消除衰减直流分量的能力进行了评估,并与传统傅里叶算法的计算结果进行了比较.仿真结果表明,改进的傅里叶算法可以有效地消除衰减直流分量的影响,其幅值响应的结果不含震荡,图形快速地收敛于稳定值.这个稳定值就是包含衰减直流分量的短路全电流中的工频值.另外,改进算法的计算精确度很高,完全可以满足应用要求.

参考文献：

[1]贺家李,宋从钜.电力系统继电保护原理[M].北京:中国电力出版社,1994:20-35.

[2]杨奇逊.微型机继电保护原理[M].北京:中国电力出版社,1997:40-45.

[3]陈德树,尹项根.计算机继电保护原理与技术[M].北京:水利电力出版社:55-57.

[4]MANN B J,MORRISON I F.Digital calculation of impedance for transmission line protection[J].IEEE Trans,1971,90(1):234-244.

[5]MELNNES A D,MORRISON I F.Real time of calculation of resistance and reactance of transmission line[J].Digital Computer E.E.Trans.(I.E.Aust),1970,7(1):134-144.

[6]刘军,慕晓静,谭港.基于误差补偿傅里叶算法的微机继电保护[J].青岛科技大学学报:自然科学版,2013,34(4):431-435.

[7]周美兰,王一磊,王健.改进傅氏算法在输电线路微机保护中的应用研究[J].黑龙江大学学报:自然科学,2010,27(6):783-788.

[8]郭浩.微机保护中的改进递推傅氏算法[J].农村电气化,2006(2):59-61.

[9]李晨,张杭,张爱民,等.一种能滤除衰减直流分量的新递推离散傅氏算法[J].继电器,2005,33(17):17-20.

[10]熊岗,陈陈.一种能滤除衰减直流分量的交流采样新算法[J].电力系统自动化,1997,21(2):24-26.

[11]苏文辉,李钢.一种能滤去衰减直流分量的改进全波傅氏算法[J].电力系统自动化,2002,26(23):42-44.

[12]RAMMAMOORTY M.APPlication of digital computer to power system protection[J].Journal of Inst.Eng.(India),1972,52(10):10-22.

[13]张举.距离保护中若干问题的研究[D].北京:华北电力大学,2003.

[14]刘毅华.电力系统故障检测新方法研究[D].杭州:浙江大学,2002.

[15]钱可弭,李常青.电力系统微机保护算法综合性能研究[J].电力自动化设备,2005,25(5):43-45.

[16]STRINGER N T.The effect of DC offset on current-operated relays[J].IEEE Transactions on Industry Applications,1998,34(1):30-34.

[17]黄纯,潘华,江亚群.一种消除非周期分量的交流采样数据修正法[J].继电器,2001,29(8):10-12.

(编辑白林雪)

Methods of Extracting Fundamental Component inShort-circuit Voltage and Current

JI Liang, JIANG Enyu

(School of Electrical Engineering,Shanghai University of Electrical Power, Shanghai200090, China)

Abstract:An algorithm which can eliminate the effect of decaying direct current (DC) component on DFT based phasor estimation is proposed.The proposed technique is based on the elimination of the phasor of a sinusoidal wave corrupted by a DC component.The results of simulation show the proposed algorithm has a great accuracy in fundamental frequency component extraction.

Key words:Fourier transform; fundamental component extracting; microprocessor-based protection; decaying DC component

中图分类号：TM771; O174.2

文献标志码：A

文章编号：1006-4729(2015)06-0519-06

通讯作者简介：季亮(1985-),男,博士,讲师,江苏南通人.主要研究方向为继电保护、故障测距、信号处理与电力系统通信.E-mail: jihome2002@sina.cn.

收稿日期：2014-09-24

基金项目：上海绿色能源并网工程技术研究中心资助项目(13DZ2251900).

DOI：10.3969/j.issn.1006-4729.2015.06.004