基于CAR模型的短期光伏发电量预测
李 芬, 钱加林, 杨兴武, 赵晋斌, 刘建锋
(上海电力学院 电气工程学院, 上海 200090)

基于CAR模型的短期光伏发电量预测
李芬, 钱加林, 杨兴武, 赵晋斌, 刘建锋
(上海电力学院 电气工程学院, 上海200090)
摘要:利用灰色关联度分析影响光伏发电量的关键气象环境因子,结合光伏电站历史数据,基于CAR模型建立了短期光伏发电量预测模型.以华中科技大学电力电子研究中心18 kW并网光伏电站资料进行预测试验,并通过调整模型参数获得了适合的模型,结果验证了该方法的有效性.应用结果表明,天气良好时,预测精度较高.
关键词:灰色关联度; 多变量时间序列; 预测; 光伏发电量
随着世界人口的不断增长,以及经济的持续发展,对于能源的需求量日益增加,煤炭、石油等化石燃料在能源消费结构中仍占较大比例.[1]如何更加有效地应用新能源渐渐成为人们关注的焦点,发展风能太阳能等清洁可再生能源将是人类社会减少温室气体排放、应对和减缓气候变化的重要手段,清洁可再生能源也将成为世界可再生能源体系的重要支柱.如今,风能的利用技术已较为成熟,并逐渐走上发展的快车道.[2]但对于太阳能光伏发电功率预测方面仍然缺乏深入的研究.
对于光伏发电系统来说,太阳能光伏发电量预测是不可缺少的一部分.[3]国内外光伏发电量预测现有方法主要分为统计法与物理法.统计法主要有:时间序列法,如自回归滑动平均法,其特点为模型简单、运算量小、实现容易、预测精度低、无法适应天气非线性变化;时间趋势外推法,如灰色预测法,其特点为模型简单、运算量小,预测精度随天气状况起伏大、不稳定;点预测法,如支持向量机法,[4]其特点为算法简单、实现容易、需要参数少、预测运算量小,在简单天气状况下的预测精度较高,但总体上预测精度不高;概率预测法,如分位数回归森林法,其特点为算法复杂、输入变量多、不易实现,预测精度较高;智能预测法,如神经网络法,[5-7]其特点为预测模型算法复杂、运算量大、学习能力强、能够适合复杂天气,在简单和复杂天气状况下的预测精度都比较高.
物理法主要有电子元件模型法、简单物理模型法和复杂物理模型法.[4]目前,时间序列法在负荷预测中应用较多,而在光伏发电预测的应用较少.[8-12]多变量时间序列模型的应用已经很广泛,例如在水文领域和生态领域等都取得了良好的应用效果,然而应用在光伏发电预测方面尚属少见.
本文利用时间序列多变量自回归,从多变量时间序列中提取了有用的信息,描绘复杂系统的动态特性,从而建立了光伏发电预测模型.以华中科技大学电力电子研究中心18 kW并网光伏电站为例,分析了夏季发电量随水平总辐射量、日照时数、平均温度等的变化规律,运用多变量时间序列分析技术建立了光伏发电量预测的动态模型,以期为光伏发电的预测提供参考.
1多变量时间序列CAR模型
CAR模型主要有两种建模方法:一是混合回归建模方法,应用了最小二乘法;二是递推最小二乘法,这是进行模型参数估计的方法.本文采用第2种方法建立CAR模型.
为了不失一般性,假定用m个变量的时间序列组n阶CAR模型,其形式为:
(1)
对该模型采用递推最小二乘法进行参数估计,由如下3个步骤组成.
1.1 递推最小二乘法参数估计方法
令
那么,CAR模型的一般形式可以写为:
(2)

(3)
式中:α——遗忘因子,一般取0.9~1.0.
如果要求遗忘历史数据的速度更快些,则α应趋于0.9;反之,α应趋于1.0;显然,若α=1,历史数据就永远不会被遗忘.为了避免在zt中yt-1和xj,t(j=1,2,3,…,m)出现负下标,不妨假设从时刻t=n开始递推,并令初值均为零.参数yt-1的初值为λΙ,其中λ取104,Ι为单位矩阵.

(4)
1.2 最高阶n的F判决器

(5)
式中:V1——低阶模型的残差平方和;
V2——高阶模型的残差平方和;
n1——低阶模型的参数个数;
n2——高阶模型的参数个数;
N——观察数据组个数.
对于相邻的两个模型CAR(n)和CAR(n-1),其统计量为:
(6)
在式(5)和式(6)中,S(n)相当于V1,S(n+1)相当于V2.分析时,取置信度α=0.05,大均方自由度为m,小均方自由度为N-mn-(m+1),求出相应的临界值Fα.根据计算所得的F值和相应的临界值Fα进行判断:若F 可依据模型的白噪声εt以及参数估计值的误差协方差阵,进行模型真实阶和时滞的F统计检验.模型白噪声εt的标准差的无偏估计为: (7) (8) (9) 由此可得模型真实阶和时滞的F判决器如下: (2) 在删除部分检验不显著的参数后,反复利用递推最小二乘法,进一步建立较为合适的CAR(n)模型. (3) 利用F检验方法对建立的模型进行显著性检验,若显著,则CAR(n)模型是真实模型;否则,参数相对较少的CAR(n)模型为最终模型. 经过以上3个步骤后,可建立较为理想的预测模型,且该模型只考虑了对系统影响较大的系数CAR(n). 2CAR模型在武汉地区光伏发电预测中的应用 本文利用华中科技大学电力电子研究中心18 kW并网光伏电站夏季(2010年7月)逐日的发电量资料,以及武汉市东西湖慈惠农场的国家一级辐射观测站武汉站(E114.03°,N30.36°)逐日的水平面太阳总辐射(MJ/m2)、日照时数(h)等同期辐射观测数据,以及武汉站常规气象要素资料,应用DPS统计软件进行灰色关联度分析和数据标准化处理,分辨系数ρ取0.5. 影响光伏上网发电量的8个因子分别为:平均气温(℃)、气温日较差(℃)、平均水汽压(hPa)、平均相对湿度(%)、平均风速(m/s)、日照时数(h)、能见度(km)、水平面总辐射(MJ/m2).各影响因子与交流发电量之间的关联系数,见表1.其中,水平面总辐射量、日照时数、平均气温、气温日较差、能见度与交流发电量间的关联系数均大于0.7. 表1 各因子与交流发电量关联系数 从物理意义上分析,在相同状况下,日照时数越长,到达地面的太阳总辐射越大,光伏组件的发电量必然越多.气温是表征太阳辐射的一个间接参数,气温与太阳总辐射存在较为明显的正相关关系.一天之中,气温最高值与最低值之差即为气温日较差,由于晴天时,大气对太阳辐射的削弱作用和保温作用更弱,因此晴天的日较差比阴雨天大.能见度是反映大气透明度的一个指标,与天气情况密切相关,阴雨天必然比晴天的能见度要低,能够穿透大气层的辐射量也较小. 根据华中科技大学电力电子研究中心18 kW并网光伏电站2010年7月的资料,以交流发电量为输出变量,以水平面总辐射、日照时数、平均温度、日较差、能见度为输入变量,建立CAR模型.采用DPS数据处理系统进行数据分析. 该模型的最高阶及时滞F测验的显著水平取0.05,递归最小二乘遗忘因子值取1.经分析,模型定阶检验结果为:CAR(n)残差平方和S(n)=0.217 9,CAR(n-1)残差平方和S(n-1)=0.279 2,模型定阶的F检验值为0.220 8.对模型真实阶进行判定,由分析结果可以得到,F检验值可判断是否剔除不显著因子,该模型中,F=0.077 3,F(α=0.05)=3.098 4,设定S=0.272 9为阶次模型全参数时的残差平方和,选定阶次、剔除不显著因素后建模的残差平方和S=0.276 1. 将不显著项剔除后,可以得到光伏发电量的CAR预测模型为: y(t)=-0.144 263y(t-1)+0.375 603x(1,t)+ 0.620 383x(2,t)+0.584 041x(2,t-1)+ 0.794 289x(3,t)-1.042 251x(3,t-1)+ 0.288 214x(4,t-1)+0.389 418x(5,t) (10) 式中:t——时间序列编号,t>1. CAR模型的预测结果如表2所示. 表2 2010年7月CAR模型的预测结果 注:天气状况空白处表示晴或多云. 从表2可以看出,在建模拟合期间,有6天相对误差低于5%,其中有两天雷暴天气,发电量大于15 kW,且误差小于2%,由此可见短暂雷暴天气对日发电量的影响不一定大;11天的相对误差在5%~15%,其中仅有1天的发电量低于10 kW;10天的相对误差超过30%,阴雨天发电量偏小,均低于5 kW,可为实际应用提供参考;还有2天的相对误差在30%左右,而这2天的能见度相对较低,均为7 km,由此可以看出能见度对发电量的影响很大.此外,表2中最后一组数据是利用该模型对2010年8月1日发电量进行预测检验,其相对误差为7.7%,预测效果较为精确. 为验证模型的预测效果,对比2010年7月份电站日发电量的观测值与上述模型的拟合值,所得曲线如图1所示. 从图1可以看出,预测曲线较好地跟踪了观测曲线的变化趋势.当然中间仍然有误差较大的预测点,较大的误差均是由恶劣天气造成的,有待于进一步深入分析. 图1 2010年7月电站日发电量拟合值与观测值对比 为进一步验证该模型的有效性,利用SPSS统计软件建立多元线性回归模型,对华中科技大学并网光伏电站发电量进行了拟合.图2为CAR模型的拟合值与观测值的对比图.图3为多元线性回归模型的对比图.比较图2和图3可以看出CAR模型的拟合精度较高. 图2 CAR模型拟合值与观测值对比 图3 多元线性回归模型拟合值与观测值对比 3结论 (1) 灰色关联方法是一种较好的选择预测因子的方法,其8个影响因子中的气温日较差对光伏发电量的影响较大. (2) 在天气状况较好的情况下,CAR模型的预测精度较高.模型预测值与实测值的相关系数较高,证明了预测结果较为可靠. (3) 考虑到恶劣天气状况对预测结果的影响较大,在后续工作中,可以将该模型与其他模型相结合进行组合预测. 参考文献: [1]杨金焕,于化丛,葛亮. 太阳能光伏发电应用技术[M]. 北京: 电子工业出版社,2009:32-33. [2]申彦波,程兴红,赵东. 气象与太阳能生态城[M]. 北京: 中国建筑工业出版社,2013.150-151 [3]李芬,陈正洪,成驰,等. 太阳能光伏发电量预报方法的发展[J]. 气候变化研究进展,2011,7(2): 136-142. [4]栗然,李广敏. 基于支持向量机回归的光伏发电出力预测[J]. 中国电力,2008,41 (2): 74-78. [5]陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9):153-158. [6]代倩,段善旭,蔡涛,等. 基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J]. 中国电机工程学报,2011,31(34): 28-30. [7]袁晓玲,施俊华,徐杰彦. 计及天气类型指数的光伏发电短期出力预测[J]. 中国电机工程学报,2013,33(34): 57-64. [8]崔洋,孙银川,常倬林. 短期太阳能光伏发电预测方法研究进展[J]. 资源科学,2013,35(7): 1 474-1 481. [9]马金玉,罗勇,申彦波,等. 太阳能预报方法及其应用和问题[J]. 资源科学,2011,33(5): 829-837. [10]姜创业,王娟敏,孙娴,等. 太阳能光伏发电量动力统计预报模式研究[J]. 水电能源科学,2012,30(6): 205-208. [11]HAN M,FAN M,XI J. Study of nonlinear multivariate time series prediction based on neural networks[M]//Advances in Neural Networks-ISNN 2005. Springer Berlin Heidelberg,2005: 618-623. [12]袁捷,仵彦卿,覃荣高. 影响 “怪潮” 发生的海洋要素多变量自回归相关分析[J]. 海洋环境科学,2013,32(5): 707-710. (编辑白林雪) LI Fen, QIAN Jialin, YANG Xingwu, ZHAO Jinbin, LIU Jianfeng (School of Electrical Engineering, Shanghai University of Electric Power, Shanghai200090, China) Abstract:The grey relational analysis is conducted to determine the meteorological environment factors with the highest impact on photovoltaic power generation. Then the key factors to construct a model of forecasting short-term photovoltaic power generation with the multi-variable time series CAR (Controlled Auto-regression) model based on the historical daily data. Finally,the output of photovoltaic power station is predicted. The prediction experiment is conducted based on the operational data of 18 kW grid-connected PV plant in the Power Electronics Research Center of Huazhong University of Science and Technology. An appropriate model is obtained by adjusting model parameters. The experiment results verify the validity of this method,and indicate that the precision of the prediction is relatively high in a good weather condition. Key words:grey relational; multi-variable time series; forecast; photovoltaic power generation 中图分类号:TM615.2 文献标志码:A 文章编号:1006-4729(2015)06-0514-05 基金项目:国家自然科学基金青年项目(51307105);上海市高校青年教师培养资助计划(ZZsd113016);上海电力学院人才基金项目(K2013-010). 通讯作者简介:钱加林(1986-),男,在读硕士,江苏淮安人.主要研究方向为太阳能光伏发电并网控制及功率预报技术研究.E-mail:brookianafly@163.com. 收稿日期:2015-04-06 DOI:10.3969/j.issn.1006-4729.2015.06.0031.3 真实阶及其时滞的F检验判决器
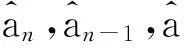



2.1 变量选取与数据预处理

2.2 模型建立
2.3 结果分析


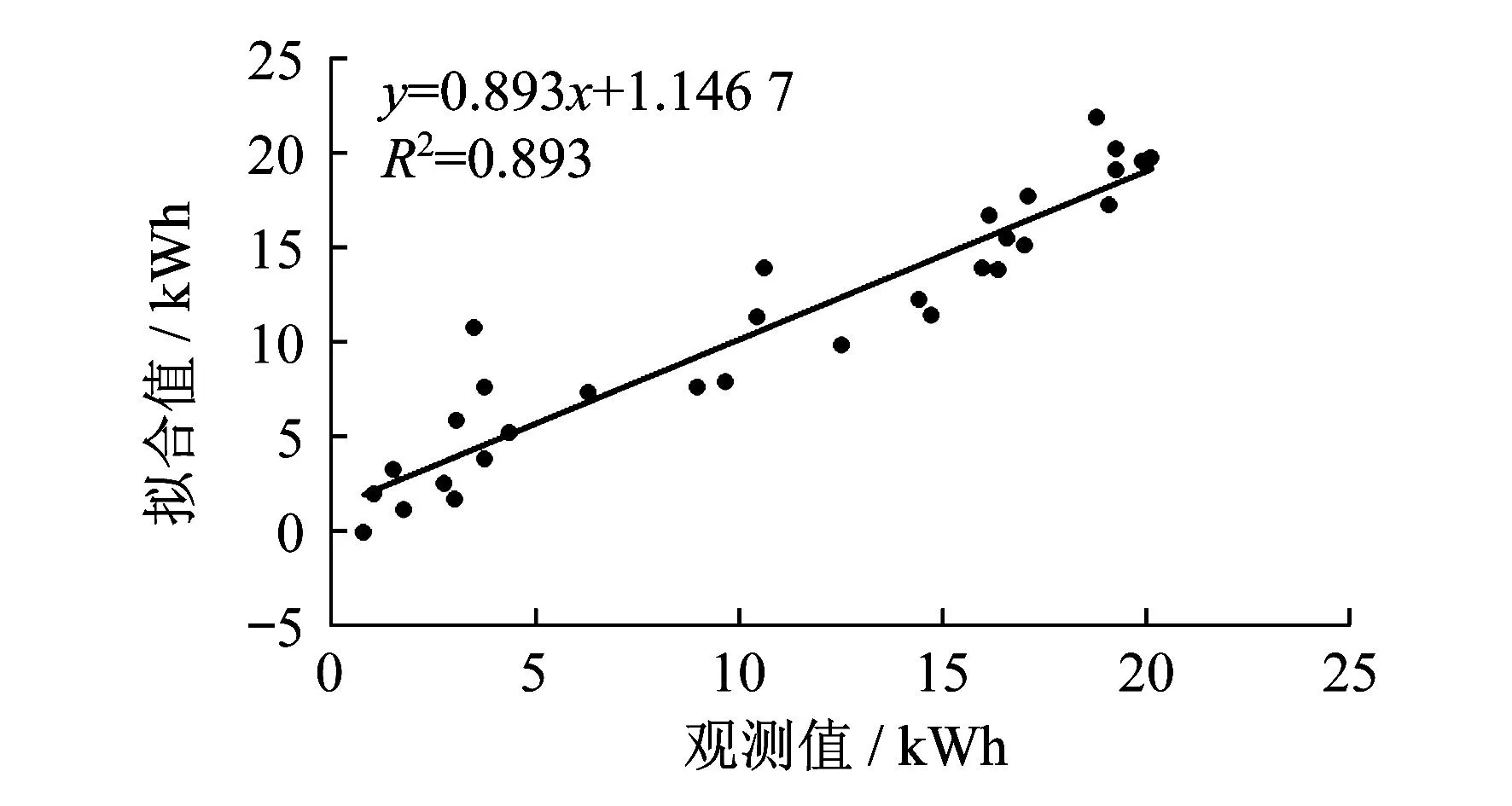
2.4 模型比较

Forecasting Short-term Photovoltaic Power Generationon CAR Model Basis

