测量放线技术中的要点和创新运用解析

■邹兵

（重庆市勘测院 重庆 400020）

测量放线技术中的要点和创新运用解析

■邹兵

（重庆市勘测院 重庆 400020）

建筑工程中的测量放线技术是建设过程中各工种、各阶段施工的基本依据，是建筑物的机构尺寸各方面符合设计要求的重要保障。建筑工程施工测量放线技术是一项复杂的系统性工作，技术要求比较高。建筑工程施工测量放线是在施工控制网的建立基础上对建筑物进行放线工作，按照建筑工程设计图纸的具体要求和施工过程中的相关规定，将设计图纸中的图形展现到实际施工现场平面上，并且进行指导和施工。建筑工程的测量放线工作贯穿于工程施工的整个过程中，对于建筑工程建设具有重要意义。本文从测量放线技术的主要内容入手，分析了测量放线工作的主要技术和创新应用。[关键词]测量放线技术内容技术应用

建筑工程测量放线技术是建筑工程项目施工人员必备的一项基本技能。做好测量放线工作，可以确保建筑工程建设的顺利施工。近年来，建筑工程测量放线工作施工过程中，出现越来越多的放线错误问题，建筑工程中放线错误会造成房屋错位，不能充分发挥其基础的设施功能。提高建筑工程测量放线工作的质量能够大大提高建筑工程的施工质量。在建筑工程施工过程中，测量放线工作主要指的是按照设计图纸要求根据具体的施工进度测量出地平面的位置和标高。建筑工程放线工作是建设施工的首道工序，因此做好测量放线工作具有重要意义。

1 测量放线工作的主要内容

1.1 前期准备阶段

在工程施工的前期准备阶段，测量放线相关工作人员需要认真阅读工程设计图纸，全面掌握工程建设施工中的工作要点，例如技术要求、工程规模和建筑物之间的联系等。同时也需要对设计院移交的高程点和坐标点数据进行准确复核，在满足精度要求的基础上，需要对高程点进行加密工作，对坐标点进行栓桩工作，避免施工过程中破坏基础点，从而影响施工进度。测量放线人员需要根据建筑工程施工要求制定出科学合理的施工测量方案，确保建筑工程施工的顺利开展。

1.2 施工阶段

施工过程中，测量放线工作人员需要根据施工进度的具体要求进行施工放线工作，需要在施工现场对建筑物的角点、高程点、轴线和竖向控制线的引入进行标注，从而确保建筑物的建设施工符合工程设计要求和标准规范。对于已经完成的工序必须进行严格的检查，避免出现放线错误，影响正常工程施工。在建筑施工过程中，必须对部分特殊位置进行水平位移观测和沉降观测，全面掌握施工的整体情况，避免出现重大施工事故，确保安全施工[1]。

1.3 竣工阶段

建筑工程施工完成后，需要进行相应的竣工验收工作，主要针对建筑物的垂直度、平面位置和其他部位的尺寸等进行检验核对，检查其是否符合工程设计要求，为工程质量的评定工作提供依据。建筑工程竣工后，需要根据竣工验收材料和工程设计资料绘制相应的竣工图纸，主要用于后期对建筑工程的维护和使用。

2 测量放线技术的特点

建筑工程前期勘察设计阶段的测量工作指的是实际的地形特征按照一定比例绘制成设计图纸，工程施工过程中的测量放线工作指的是将设计图纸中的图形位置、图形尺寸和高程等因素体现在具体的施工现场中，为接下来的施工工作提供依据。因此测量放线工作必须要认真仔细，防止出现放线错误，影响建筑工程的施工进度和施工质量。

测量放线工作贯穿于整个建筑工程施工过程中，特别是大型建筑工程，建筑物相对比较复杂，对测量放线工作的准确性要求更高，为了避免在测量放线过程中受到工程施工的影响，测量放线工作人员必须严格按照规定程序进行放线。必须坚持先整体后局部的基本原则：首先确定出建筑物的主轴线所在的位置，进而确定出其他各部位辅助轴线的位置，利用尺寸和形状对建筑物进行设计。在建筑工程施工测量放线时，首先通过设计图纸中的点坐标和高程数据布设相应的控制网，再利用控制网确立出主轴线的位置，并随即确定出其他辅助轴线的位置，然后依据尺寸和形状将建筑物反应到实际的施工现场中。通过这种测量放线方法能够确保各元素之间的几何关系，有利于对工程施工进行指导[2]。

3 测量放线技术的创新应用

3.1 经纬仪放样法

3.1.1 圆曲线主点放样

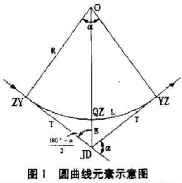
如图1所示，已知圆曲线的半径是R，线路转向角为α。根据公式求圆曲线的切线长T、外矢矩E、切曲差q和圆曲线长L。

T=R·tgα/2，L=π/180·α·R E=R·（secα}/2-1），q=2T-L

圆曲线的主点放样过程主要是：将经纬仪放到焦点JD处，用线路方向进行定向。从JD开始沿着两个切线方向分别测量出其切线长度T，从而得到圆曲线的起点ZY和终点YZ。在交点JD处后视ZY,然后拨（180°-α）/2的角，得到其分角线的方向，沿着分角线的方向从JD处量出外矢矩E，从而得到圆曲线的中点QZ。

3.1.2 圆曲线细部点放样

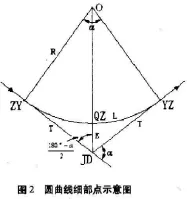
最常见的方法就是偏角法。如图2，要想对圆曲线上2点进行放样，应该在ZY处放置镜子，再后视JD点，从而拨出偏角δ2，再从1点和拨出的视线方向做定长为c的交会，从而得到2点[3]。

偏角值的计算。偏角δì在几何学中指的是弦切角。根据弦切角=圆曲线弧长所对的圆心角的一半，可得：

δ=Φ/2=c/2R·180°/π

3.2 极坐标放样法

3.2.1 计算圆曲线的主点和细部点坐标

已知各个交点JDi的坐标、圆曲线的半径为R、圆心角为α，并且圆心角=偏角α。

3.2.1.1 计算圆曲线的主点坐标

根据公式T=R·tgα/2，可得切线长T；

根据JD2与JD1的坐标反算出αJD2-JD1；

根据JD2的坐标、切线长度T和αJD2-JD1正算出圆曲线的起点ZY的坐标；

根据JD2的坐标、切线长度T和αJD2-JD3正算出圆曲线的终点YZ的坐标；

根据αJD2-JD1、β角=90°推算出αZY-O；

根据ZY的坐标、圆曲线的半径为R和αZY-O正算出圆心O点处的坐标；

根据αZY-O、水平夹角为α/2推算出αO-QZ；

根据圆心O点的坐标、圆曲线半径R和αO-QZ推算出圆曲线中点QZ的坐标。

3.2.1.2 计算圆曲线的细部点坐标

根据加密桩1,2,3,……，i之间的弧长c计算出圆曲线弧长所对圆心角Φi

P2[文献码]B

1000-405X（2015）-11-185-2