海上弱固结砂岩储层膨胀注水工艺研究

彭成勇　(中海油研究总院，北京 100027)

徐康泰（石油工程教育部重点实验室（中国石油大学（北京））中国石油大学（北京）石油工程学院，北京102249）

于继飞，曹砚锋　(中海油研究总院，北京 100027)

王雷，崔楠（石油工程教育部重点实验室（中国石油大学（北京））中国石油大学（北京）石油工程学院，北京102249）

海上弱固结砂岩储层膨胀注水工艺研究

彭成勇(中海油研究总院，北京 100027)

徐康泰（石油工程教育部重点实验室（中国石油大学（北京））中国石油大学（北京）石油工程学院，北京102249）

于继飞，曹砚锋(中海油研究总院，北京 100027)

王雷，崔楠（石油工程教育部重点实验室（中国石油大学（北京））中国石油大学（北京）石油工程学院，北京102249）

[摘要]针对我国渤海弱固结砂岩油田注水井近井污染问题,提出膨胀注水解堵工艺技术,考虑随距井筒距离变化的污染程度,结合流固耦合效应,编写ABAQUS子程序,建立有限元分析模型,模拟渤海油田某注水井膨胀注水解堵效果。结果表明,在一定污染程度下,存在一个可达到解堵目的的最小注入速度,并在此基础上,建立渤海弱固结砂岩储层膨胀注水图版。结合实际,提出配套阶梯式膨胀注水工艺,增强现场运用的安全性和灵活性。

[关键词]弱固结砂岩;膨胀注水;污染程度;注水图版;阶梯式注水

海上弱固结砂岩高渗油田注水开发，由于注水水质、颗粒沉积等原因，注水井污染堵塞现象严重，注入压力上升明显[1，2]。针对我国渤海弱固结砂岩油田注水污染井问题，采用膨胀注水技术进行解堵[3]，即高于储层破裂压力注水，使地层产生穿透污染带区域的短裂缝，从而达到解堵目的。该工艺难点在于控制排量，即合理的注入速度；在达到解堵目的的同时，能够降低实施风险。考虑随距井筒距离变化的污染程度[4~6]，结合流固耦合效应，针对该区块某口具体注水井，采取该工艺进行解堵，模拟膨胀注水效果，给出最优注入速度。设置不同随距离变化的污染程度，建立适用于弱固结高渗砂岩储层注水井解堵的一般适用性注水图版，实现快速判断可穿透污染带的最小注入速度。根据工艺现场施工特点，提出阶梯式膨胀注水概念。

1膨胀注水模型建立

弱固结砂岩储层注水过程，受注入流体影响，岩土微观几何形状较常规储层更易发生改变，影响储层孔渗特征[7]。

岩石骨架的变形可表征为：

(1)

式中：Δe为孔隙比变化量，1；ΔVp为孔隙体积变化量，m3；Vs为固相体积，m3。

体积应变为：

(2)

式中：εv为体积应变，1；ΔV为岩石体积变化量，m3；V0为原始体积，m3；e为孔隙比，1;e0为初始孔隙比，1。

即：

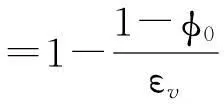
(3)

式中：φ为孔隙度，1；φ0为初始孔隙度，1。

结合渗透系数和孔隙度间的关系，得到考虑渗流-应力耦合数学公式[7,8]：

(4)

式中：K0为初始渗透系数，cm/s；K为渗透系数，cm/s。

污染程度由弱固结砂岩储层注水井近井地带污染情况测定结果[4~6]确定，可采取“三段直线型”污染模式表征近井污染情况，设定了4种不同污染程度，从小到大分别为：情况①——0~1m，井筒储层污染程度最为严重，渗透率损失率为95%，且为常数，也是影响注入效果的主要因素；1~7m内，7m时渗透率损失率下降为20%，为线性变化；7~11m内，11m时渗透率损失率为0%，即恢复原始渗透率，为线性变化；11m外渗透率无损失。情况② ——0~1m，渗透率损失率为97%，且为常数；1~9m内，9m时渗透率损失率为20%，为线性变化；9~13m内，13m时渗透率损失率为0%，为线性变化；13m外渗透率无损失。情况③ ——0~1m，渗透率损失率为99%，且为常数；1~10m内，10m时渗透率损失率为20%，为线性变化；10~15m内，15m时渗透率损失率为0%，为线性变化；15m外渗透率无损失。情况④——0~1m，渗透率损失率为99.5%，且为常数；1~11m内，11m时渗透率损失率为20%，为线性变化；11~15m内，15m时渗透率损失率为0%，为线性变化；15m外渗透率无损失。

利用ABAQUS有限元软件，建立有限元分析模型[8~12]：采用线性二维CPE4RP单元对模型进行网格划分。考虑近井区域压力变化明显，对模型进行二次加密，即图1加密区1与加密区2。利用用户子程序USDFLD、UFLUIDLEAKOFF实现随距离变化的渗透率，即污染程度，利用用户子程序GETVRM实现弱固结砂岩储层流固耦合特征，即式(4)。

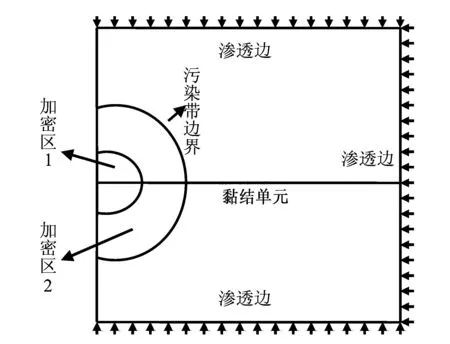
图1　计算模型示意图

2膨胀注水工艺运用

渤海某油田注水井，采用“一投三分”分层注水技术[13]，取各段参数平均值，代入所建立的有限元分析模型中。其中污染模式根据储层原始渗透率按照“三段式”的污染模式赋值，其余参数见表1。

表1　模型中基础参数

采取膨胀注水工艺进行解堵，在604、864、1296、1728、2160m3/d注入速度下施工25min，观察井底压力变化趋势，并在施工25min后，继续以200m3/d的原配注量注水，分析解堵后效果，结果见图2。由图2可知，当注入速度大于864m3/d，恢复常规注水，井底压力几乎一致，表明膨胀注水注入速度大于864m3/d ，均能达到解堵效果。864m3/d为该井施工优选值，即在这种情况下能够达到解堵目的的最小施工排量。

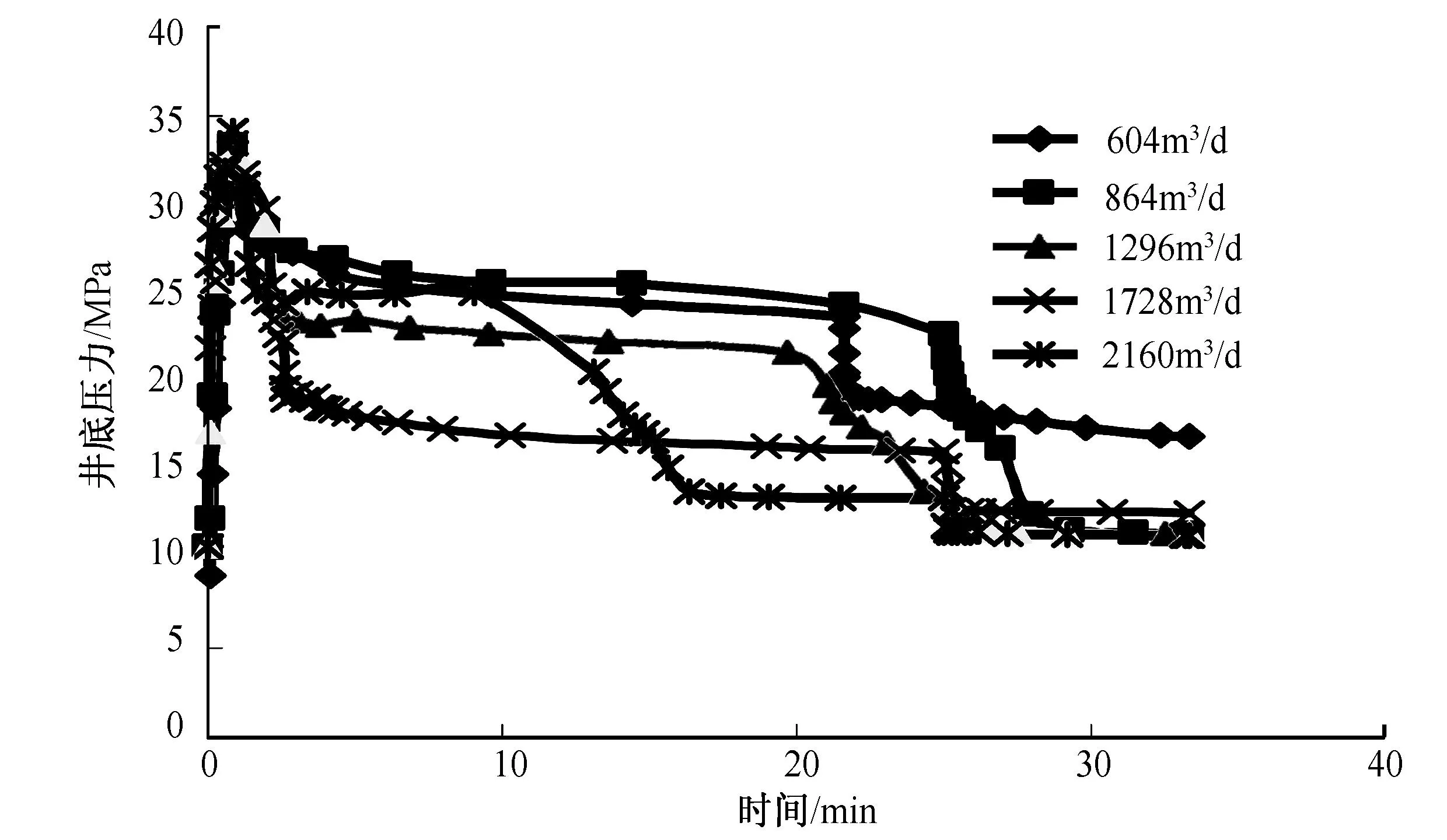
图2　注入井底压力模拟

3膨胀注水图版建立

采取所示 “三段式”污染模式，根据渤海弱固结砂岩储层基本物性，建立有限元分析模型，分析不同储层厚度、不同污染情况下，能够突破污染带，达到解堵目的的最小注入速度。根据储层特点，模板采取储层厚度为10、20、30、40、50m；上述4种不同污染程度情况如图3所示。

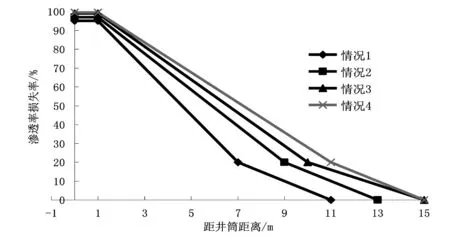
图3　污染程度情况

模型其他基本参数包括：①原始地层压力13MPa，水平最大主应力为27MPa，最小主应力为22MPa；②初始渗透率为1000mD，初始孔隙度为0.3；③弹性模量为1.8 GPa，泊松比为2.64。如图4所示，得到适合于分析我国渤海弱固结砂岩储层注水井污染膨胀解堵注水图版。运用该图版：假设一污染井，污染程度类似图3中的情况2，作用储层厚度约为30m，则达到解堵目的的最小注入速度约为2000m3/d。

图4　最小注入速度图版

4阶梯式膨胀注水工艺提出

结合现场运用，提出阶梯式膨胀注水概念，即逐步提高排量技术。如图5所示，分5个阶段升排量注入，每阶段施工25min，即300m3/d(25min) +518m3/d(25min)+864m3/d(25min)+1296m3/d(25min)+1728m3/d(25min)；与常规膨胀注水(1728m3/d(25min))对比，可知阶梯式注水工艺技术优势如下：①井底最大压力降低，达到6.30MPa，较大幅度降低了施工所需最大压力，即降低了对设备性能的要求和施工难度；②有利于现场施工调整；③整体施工趋势更平稳，降低了施工带来的风险。

图5　注入井底压力模拟(阶梯式膨胀注水)

5结论

1)考虑流固耦合效应，结合随距井筒

距离变化的渗透率特征，即“三段式”污染形式，建立有限元分析模型，该模型适合于分析渤海疏松砂岩油藏注水井膨胀注水解堵过程。

2)以渤海疏松砂岩油藏某口污染注水井为例，采用膨胀注水技术，模拟注水过程井底压力变化情况，得到可达到解堵目的的最小注入速度。

3)考虑“三段式”污染形式，建立膨胀注水图版，该图版能够根据不同储层厚度、不同污染情况，快速确定达到解堵目的的最小注入速度。

4)提出阶梯式膨胀注水工艺，较之于常规膨胀注水，该工艺具有逐步增大注入量、施工所需最大压力小、持续作业压力平稳的特征，从而具备降低设备性能要求、便于调整施工方案、降低施工带来的风险等优势。

[参考文献]

[1]沈燕来, 刘德华. 渤海绥中36-1油田注水井堵塞原因分析及解堵增注试验[J]. 油气采收率技术, 1999, 6(4): 57~61.

[2]Chin L Y, Montgomery C T. A numerical model for simulating solid waste injection in soft rock reservoirs[J].SPE90507, 2004.

[3] Xu B, Yuan Y, Wong R C K. Modeling of the hydraulic fractures in Unconsolidated Oil Sands Reservoir[A]. American Rock Mechanics Association. 44thUS Rock Mechanics Symposium and 5thUS-Canada Rock Mechanics Symposium[C].Salt Lake City, Utah, 2010-06-27.

[4] Total Fina Elf. Butiaba Conceptual Studies [Z]. Paris:Workshop PWRI, 2011-08-02.

[5] Al-Abduwani F A H, Shirzadi A, van den Brock W, et al. Formation damage vs. solid particles deposition profile during laboratory simulated PWRI[J]. SPE Journal, 2005, 10(2): 138~151.

[6] Bedrikovetski P, Furtado C, de Souza A, et al. In-situ erosion of damaged formation during injectivity decline (PWRI & seawater flood)[A].7thEuropean Formation Damage Conference[C].Scheveningen, the Netherlands,2007-05-01.

[7] 陈卫忠, 伍国军, 贾善坡. ABAQUS 在隧道及地下工程中的应用[M]. 北京：中国水利水电出版社, 2010:235~236.

[8]Hibbitt, Karlsson, Sorensen. ABAQUS/Standard user's manual[Z]. Hibbitt, Karlsson & Sorensen, 2001.

[9]Lian Z L, Wang X X, Wu H A, et al. Modeling and simulation of hydraulic fracturing propagation in permeable reservoirs[M]. Switzerland: Trans Tech Publications Ltd, 2006: 383~386.

[10] Huang Y. A user-material subroutine incroporating single crystal plasticity in the ABAQUS finite element program[M]. Cambridge: Harvard Univ, 1991.

[11] Abou-Sayed A S, Zaki K S. A mechanistic model for formation damage and fracture propagation during water injection[J]. SPE94606-MS,2005.

[12]Souza A L S, Fernandes P D. The impact of injection with fracture propagation during waterflooding process[J]. SPE94704-MS,2005.

[13]刘义刚. 渤海油田控水工艺技术新进展[M]. 北京：化学工业出版社,2012.

[编辑]黄鹂

[引著格式]彭成勇，徐康泰，于继飞，等.海上弱固结砂岩储层膨胀注水工艺研究[J].长江大学学报(自科版) ,2015,12(26):77~80.

[中图分类号]TE53

[文献标志码]A

[文章编号]1673-1409(2015)26-0077-04

[作者简介]彭成勇(1981-)，男，硕士，工程师，主要从事非常规油气开发增产工作， pengchy@cnooc.com.cn。

[基金项目]中海石油(中国)有限公司科研项目(CCL2012RCPS0259RSN)。

[收稿日期]2015-04-20