基于三孔隙度复合变量的地层岩性模糊模式识别研究

范翔宇

杨杨　(中石油青海油田分公司勘探开发研究院，甘肃 敦煌 736202)

段美恒，赵鹏斐，刘璐，徐烽林　(西南石油大学石油与天然气工程学院，四川 成都 601500)

基于三孔隙度复合变量的地层岩性模糊模式识别研究

杨杨(中石油青海油田分公司勘探开发研究院，甘肃 敦煌 736202)

段美恒，赵鹏斐，刘璐，徐烽林(西南石油大学石油与天然气工程学院，四川 成都 601500)

[摘要]由于非试验手段的传统岩性识别方法往往具有一定的模糊性和多解性,故利用岩心观察和薄片分析难以对全井眼地层剖面岩性进行描述。然而最及时的岩屑录井资料携带信息量又有限,且受人为因素影响较大,因此地层岩性仍然是一个值得探讨的研究对象。模糊模式岩性识别具有信息容量大、易进行程序化快速实现及同时充分利用自然伽马、中子、声波时差、密度和电阻率等测井数据蕴涵的岩性信息,在不提供取心样本的情况下,自动对原始测井数据进行分析分类,并对全井段岩性进行连续划分等优势。为了能够充分利用地层测井信息提高岩性识别精度,其构建了同时考虑声波时差、中子、密度、自然伽马和电阻率信息在内的新的三孔隙度复合变量,并将该复合变量作为模糊模式岩性识别的输入参数;同时基于模糊理论编制了岩性快速识别软件,该软件采用多种贴近度计算模型来开展岩性分析,可以录入多条测井曲线对大量井剖面岩性进行连续判别,能够适用于不同复杂地层的岩性识别需求。基于三孔隙度复合变量的地层岩性模糊模式在普光气田的应用结果表明,该方法识别精度高,应用前景广阔。

[关键词]岩性识别;模糊模式;孔隙度复合变量;软件

目前，多途径、多手段、多学科交叉融合成为油气勘探开发技术的发展趋势，岩性识别已经逐步进入到人工智能阶段。近年来，模糊集合理论有了很大发展，引起了控制论、图像识别、计算机等科学工作者的极大关注。鉴于岩性判别中存在的模糊性和多解性，笔者提出了基于模糊模式识别理论的测井识别方法。实践证明，模糊数学理论能有效地解决、处理对象的模糊性问题，从而得到较精确的结论。

测井曲线对岩性的敏感差异主要取决于组成岩石矿物成分的种类不同，模糊模式识别选择的测井参数合适与否对岩性识别结果影响很大，而声波时差、中子孔隙度、密度孔隙度的三孔隙度曲线以及自然伽马、电阻率曲线对地层岩性有很好的反映。该次研究选取声波时差、中子孔隙度、密度孔隙度测井信息构建得到的3个新的复合变量(M、N、P)，并将新复合变量和自然伽马、电阻率曲线相结合作为模糊模式岩性识别的输入参数；同时根据模糊模式识别理论编制了岩性识别软件，软件采用标准差变换和极差变换消除数据量纲，并对多种贴近度计算模型进行优选，很好地解决了由于各类信息源量纲不同而不能直接归一化处理和岩性解释的困扰，保证了基于三孔隙度复合变量的岩性模糊模式识别软件能够很好地适应不同地层岩性判别的需要。

1模糊模式识别原理及数据预处理

模糊模式识别问题中的被识别对象一般不是论域中确定的元素，而是论域的一个子集，或是普通子集，或是模糊子集。当识别对象为集合时，所涉及到的不是元素与集合的隶属关系，而是模糊子集之间的贴近程度。贴近度是描述模糊集合之间接近程度的一种衡量方法，隶属集合应用范畴。测井参数集合可以看作是无确定边界的模糊集合，对于模糊的待识别对象，更加适用模糊贴近度方法来进行处理[1~4]。

1.1　模糊模式识别原理及方法

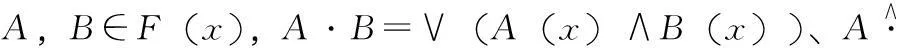
1)格贴近度设A,B∈F(x)，令：

N(A，B)g=(A·B)∧(A·B)c

(1)

式中：N(A,B)g为模糊集合A与B的格贴近度；(A·B)c为A与B内积的余集。

2)海明贴近度若论域X={x1,x2,…,xn}，则：

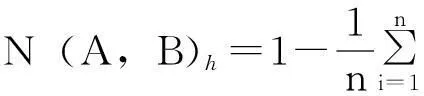
(2)

若论域X=[a,b]⊆R，则：

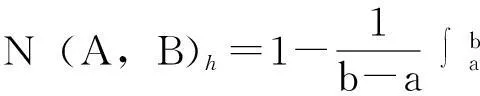
(3)

式中：N(A,B)h为模糊集合A与B的海明贴近度；x1,x2,…,xn为集合元素；a、b为实数。

3)欧式贴近度若论域X={x1,x2,…,xn}，则：

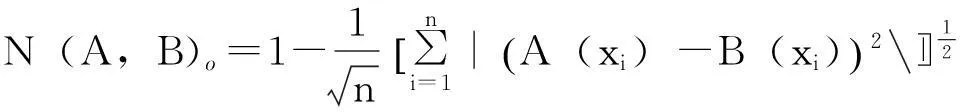
(4)

若论域X=[a,b]⊆R，则：

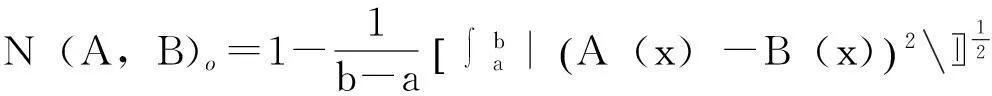
(5)

式中：N(A,B)o为模糊集合A与B的欧式贴近度。

4)最大最小贴近度若论域X={x1,x2,…,xn}，则：

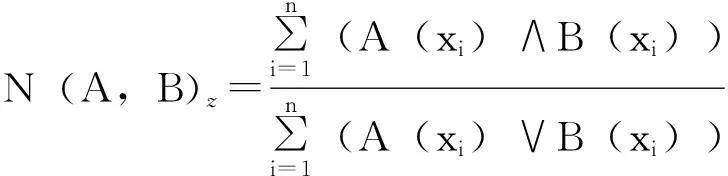
(6)

式中：N(A,B)z为模糊集合A与B的最大最小贴近度。

5)算数平均贴近度

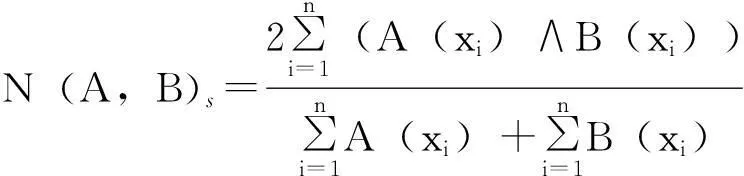
(7)

式中：N(A,B)s为模糊集合A与B的算数平均贴近度。

6)测度贴近度设A(x)，B(x)是测度空间(X,σ(X),μ)上的函数，则可定义：

(8)

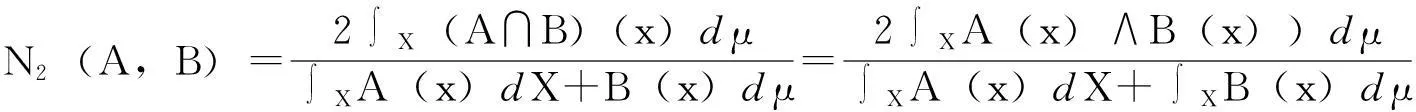
(9)

式中：N1(A，B)、N2(A，B)为测度贴近度；σ(X)为模糊代数；μ为σ(X)上的模糊测度。

1.2　模糊模式识别数据预处理

为了解决测井数据单位不统一而不能直接汇总的问题，笔者引用标准化方法对测井数据进行无量纲化处理。标准化处理方法是一种常用的消除量纲影响的方法，该方法是在假定变量服从正态分布的前提下，将变量值转化为数学期望为0、方差为1的标准化数值，从而达到同度量的效果。标准化处理方法分为极差变换和标准样本变换[11~17]。

1)极差变换极差是用来衡量数据变化波动范围大小的指标，对极端值较为敏感。设有n个决策指标和m个待评价方案ai(1≤j≤m)，由m个待评价方案和n个决策指标值构成的矩阵K=(kij)m×n称为决策矩阵。在K=(kij)m×n中，对于正向指标：

(10)

(11)

式中：矩阵Yj=(yij,j)m×n为极差变换标准化矩阵；kij为实际值。

极差变换无论K中的指标值是正数还是负数，经过极差变换后标准化指标满足0≤yij≤1，逆指标均化为正向指标，最优值为1，最劣值为0。

2)标准样本变换标准样本变换中的标准差是反映数据的整体波动变化大小的指标，表示数据中各元素与该组数据的均值的情况。在决策矩阵P=(pij)m×n中，令：

(12)

经标准样本变换之后，标准化矩阵的样本均值为0，方差为1。若pij比样本均值大，经过标准化处理后，yij>0；若pij比样本均值小，经过标准化处理后，yij<0。

标准化处理不像函数化处理那样，人为地凭经验选择临界值；也不像相对化处理一样评价结构单一。目前，极差变换和标准化变换统计分析程序应用广泛，资源利用方便，发展成熟，能够很好地实现指标的标准化。

2基于三孔隙度复合变量的模糊识别模型建立

2.1　三孔隙度复合变量的构建

中子孔隙度、密度孔隙度、声波时差的三孔隙度测井曲线能够很好地反映地层岩性特征，为了充分利用三孔隙度曲线中所蕴含的岩性信息，构建了3个同时包含三孔隙度信息的、与岩石骨架性质密切相关的、新的复合变量M、N、P(其中，M是由密度孔隙度和声波孔隙度复合而成的变量；N是由密度孔隙度和中子孔隙度复合而成的变量；P是由声波孔隙度和中子孔隙度复合而成的变量)，M和N分别表示声波时差-密度孔隙度、中子孔隙度-密度孔隙度交会图上的某一岩性线的斜率；P与自然伽马的交会图能够很好地识别岩性。新的复合变量M、N、P的具体定义如下：

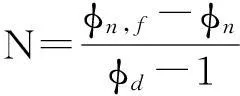
(13)

(14)

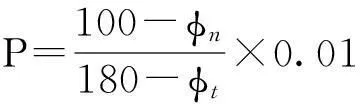
(15)

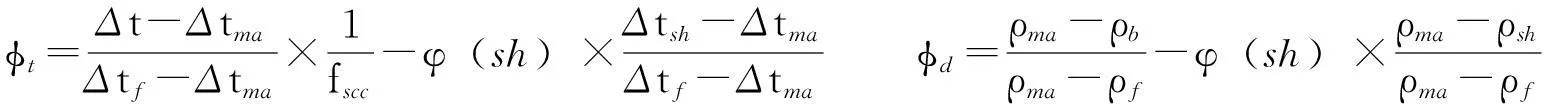
式中：Δtf为孔隙流体声波时差，μs/ft；Δtma为岩石骨架声波时差，μs/ft；Δt为井周地层任意点的声波时差，μs/ft；ρma为岩石骨架密度，g/cm3；ρf为孔隙流体密度，g/cm3；φn为地层中子孔隙度，%；φd为密度孔隙度，%；φt为声波时差孔隙度，%；φn,ma为岩石骨架中子孔隙度，%；φn,f为孔隙流体中子孔隙度，%；φ(sh)为地层泥质体积分数，1；fscc为声波压实校正因数，1；ρsh为泥岩密度，g/cm3；φnc,l为目的层补偿中子测井值，%；φn,ma,l为岩石骨架中子测井值，%；φn,sh,l为泥岩中子测井值，%;ρb为地层密度，g/cm3。

2.2　基于复合变量的模糊识别标准模型

根据普光气田岩心精细描述、录井资料以及研究区部分井的测井系列统计和测井岩性分析结果得出，普光工区研究井段岩性主要以云质灰岩、灰质白云岩、灰岩、白云岩、泥质灰岩、硬石膏、膏质白云岩、膏质灰岩为主，所以建立的标准识别模型可分为8类，由于岩性测井参数响应范围不同，每种岩性可能存在多种模型数据，分类见表1。根据标准模型计算得出的M、N、P见表2。

表1　普光气田岩性类型标准模型

注：1p.u.表示孔隙度为1%。

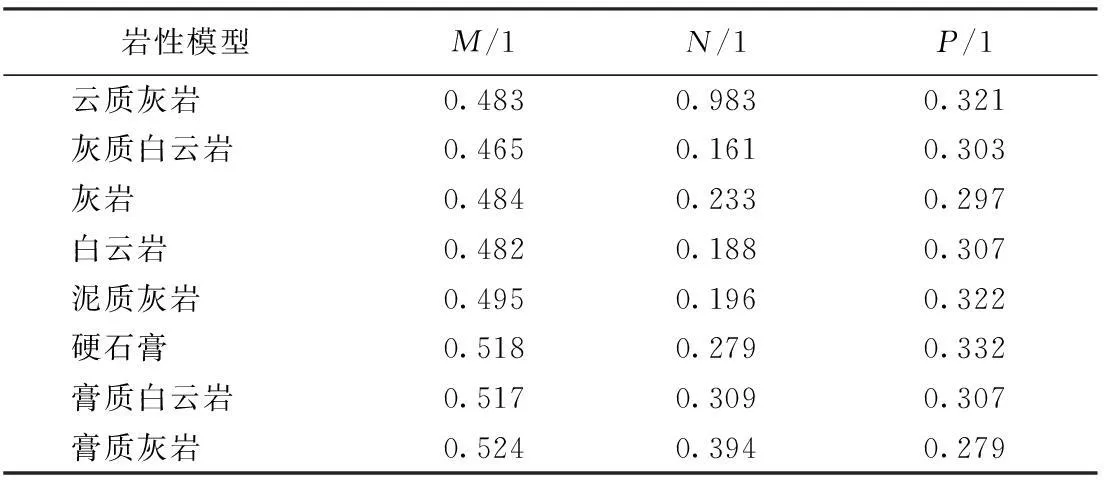
表2　岩性识别标准模型对应的M、N、P参数集

3应用实例分析

基于上述相关理论，笔者采用VB6.0语言编制了模糊模式岩性自动识别程序，并对普光气田多口井进行岩性识别分析，分析的思路流程见图1。具体岩性识别中，在数据预处理的基础上，通过极差变换、标准差变换以及贴近度方法优选等一系列运算，得出岩性识别结果，并可绘制出岩性比例图和岩性分布图(图2、3)。

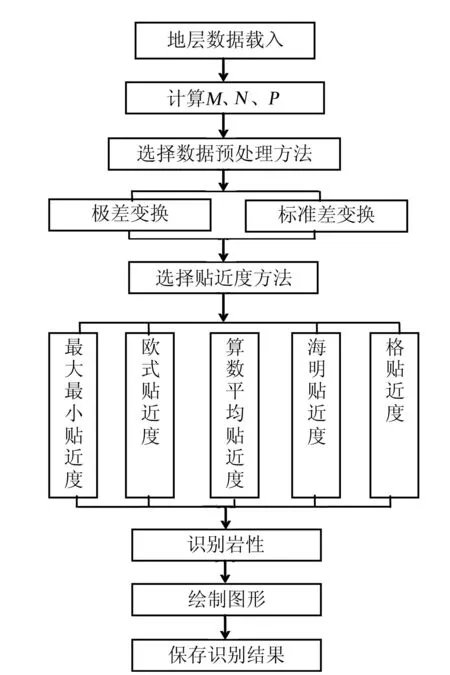
图1　模糊模式岩性识别处理流

图2　模糊模式识别岩性处理

图3　模糊模式识别岩性分布图

在研究过程中，笔者对普光气田的普光4-F1井、普光6-J2井、普光4-F3井、普光4-J2井等井的80多个层位进行了岩性识别。以普光4-F1井为例(见表3)，采用识别模式1进行岩性识别时， 20个样本中存在2个样本识别误差，符合率为90%；采用识别模式2进行岩性识别时， 20个样本中存在3个样本识别误差，符合率为85%。通过对这些井的岩性识别发现，识别模式1的符合率明显高于识别模式2。

应用结果表明，在模糊模式识别岩性时，选择不同的贴近度会得到不同的处理结果，根据研究工区地层性质及多次试算得出，普光4-F1井选择格贴近度法和最大最小贴近度法的识别结果更准确；普光4-F3井选择最大最小贴近度法的识别结果较准确；普光6-J2井选择海明贴近度和最大最大最小贴近度法的识别结果较准确；普光4-J2井选择最大最小贴近度法和格贴近度法的识别结果更准确。由此可见，最大最小贴近度法更适合研究区的实际情况，识别结果更稳定(图4)。

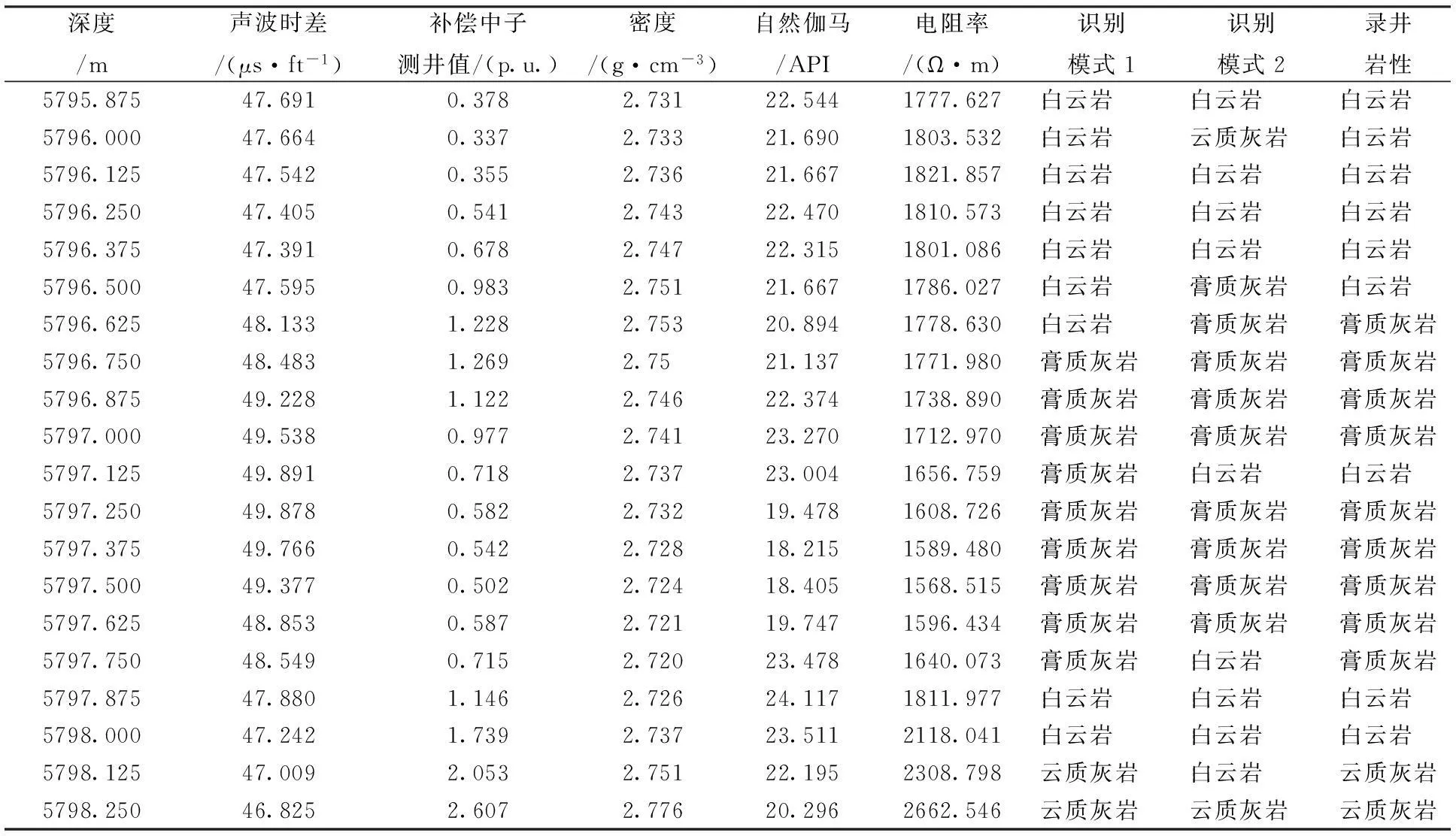
表3　普光4-F1井模糊模式识别结果

注：识别模式1为基于三孔隙度复合变量模糊模式识别；识别模式2为基于三孔隙度原始测井曲线的模糊模式识别。

图4　不同贴近度方法模型岩性识别结果对比

4结论

1)M、N、P充分利用了测井数据中的三孔隙度信息，能够综合反映岩石骨架的性质。以三孔隙度复合变量并结合自然伽马和电阻率曲线作为输入变量，与三孔隙度原始曲线作为输入变量的识别结果对比表明，基于三孔隙度复合变量的模糊模式岩性识别准确率有明显提高，为更加精确地识别岩性提供理论支持。

2)模糊模式岩性识别提供的多种贴近度模型能够适应不同地层的研究需要，根据地层性质选择不同的贴近度方法有利于提高岩性识别精度，该次研究选取的最大最小贴近度法更加符合研究区的实际情况，识别准确率较高。为了更加宏观地了解研究工区岩性信息，软件提供了岩性比例图和岩性分布图的绘制功能，同时岩性识别结果还能够保存为含有岩性标准符号的数据文件，方便快捷。根据上述研究可以得出，基于三孔隙度复合变量的模糊模式岩性识别方法准确率高，为实际应用提供理论支持，有很好的应用和推广前景，为多角度识别岩性提供了新途径。

[参考文献]

[1]范翔宇，夏宏泉，郑雷清，等.基于模糊理论的复杂岩相测井识别研究[J].钻采工艺，2007，33(2)：53～55，154.

[2]李保霖.基于测井数据的岩性识别方法研究[D].西安：西安科技大学，2012.

[3]徐海波，李瑞，邹炜，等.模糊聚类实现岩性自动划分[J].物探化探计算技术，2006， 28(4)：319～321 ，284.

[4]连增增，谭志祥，邓喀中.基于模糊模式识别的贴近度法判别煤田测井岩性[J].测井技术，2013，37(3)：285～288.

[5]张涛，莫修文.基于交会图与模糊聚类算法的复杂岩性识别[J].吉林大学学报(地球科学版)，2007，37(S1)：109～113.

[6]刘为付.模糊数学识别深层潜山碳酸盐岩岩性[J].新疆石油学院学报，2003，15(3)：35～39，85.

[7]廖太平，张福荣，张志坚. 基于模糊聚类算法的复杂岩性识别[J].大庆石油学院学报，2004 ，28(6)：58～60，113.

[8]刘明军.测井数据岩性识别软件系统的开发与应用[J].地球物理学进展，2013，28(2)：908～913.

[9]刘为付，朱筱敏. 利用模糊数学识别鄂尔多斯盆地气藏岩性[J].断块油气田，2005，12(5)：7～9，89.

[10]刘为付，孙立新，刘双龙，等. 模糊数学识别火山岩岩性[J].特种油气藏，2002，9(1)：14～17，80～81.

[11]居培，翟应虎. 基于正态分布理论的模糊综合评判法识别岩性[J].科学技术与工程，2012，12(21)：5253～5256.

[12]张晓平.基于贴近度的模糊综合评判结果的集化[J]. 山东大学学报(理学版)，2004，39(2)：25～29.

[13]刘法贵，赵娟.模糊贴近度及应用[J]. 华北水利水电学院学报，2006，27(3)：104～106.

[14]王学斌，朱满红，滕涛. 复杂岩性测井识别方法及应用分析[J]. 内蒙古石油化工，2010，17(17)：41～42.

[15]刘秀娟，陈超，曾冲，等.利用测井数据进行岩性识别的多元统计方法[J].地质科技情报，2007，26(3)：109～112.

[16]冯源. 基于模糊相似矩阵的分类方法[J].太原师范学院学报(自然科学版)，2005，4(3)：12～15

[17]安中华，安琼. 优化模糊聚类的一种方法[J].数量经济技术经济研究，2004，10(10)：77～82.

[编辑]龚丹

[引著格式]范翔宇，杨杨，段美恒，等.基于三孔隙度复合变量的地层岩性模糊模式识别研究[J].长江大学学报(自科版) ,2015,12(26):27~32.

[中图分类号]P631.84

[文献标志码]A

[文章编号]1673-1409(2015)26-0027-06

[作者简介]范翔宇(1974-)，男，博士(后)，教授，主要从事油气井岩石力学、钻井地质环境描述及灾害防治技术、测井技术在石油工程中的应用等方面的研究工作；通信作者：杨杨，568343517@qq.com。

[收稿日期]2014-11-17