应用虚拟结构的卫星编队飞行自适应协同控制

黄勇李小将杨业伟李志亮（装备学院研究生管理大队，北京 046）（2装备学院航天装备系，北京 046）（3装备学院激光推进及其应用国家重点实验室，北京 046）

应用虚拟结构的卫星编队飞行自适应协同控制

黄勇1李小将2，3杨业伟1李志亮1
（1装备学院研究生管理大队，北京 101416）
（2装备学院航天装备系，北京 101416）
（3装备学院激光推进及其应用国家重点实验室，北京 101416）

针对卫星编队飞行协同控制存在质量、转动惯量不确定性及外部扰动的问题，提出了一种应用虚拟结构的卫星编队飞行自适应协同控制方法。首先，通过对虚拟结构模型的描述，建立了虚拟结构状态变量与编队卫星期望状态之间的表达式；其次，设计了编队卫星和虚拟结构的位置、姿态自适应协同控制器，通过在虚拟结构控制器中引入编队卫星的状态误差，实现了编队信息至虚拟结构的反馈，并采用Barbalat引理证明了闭环系统的稳定性和对有界扰动的抑制；最后，以三星编队协同轨道机动和空间指向性偏转为例对所设计的控制器进行了仿真验证。仿真结果表明：设计的控制器能够实现对编队卫星质量和转动惯量的自适应估计，使得编队卫星位置和姿态控制误差最终趋近于零，验证了所提方法的有效性。

协同控制；自适应；虚拟结构；不确定性；有界扰动；卫星编队

1 引言

目前，卫星编队飞行协同控制策略主要以主从结构、行为结构和虚拟结构协同控制为主［1］，每种控制策略各有特点。其中，主从结构和行为结构编队飞行协同控制策略在星间的相对运动控制方面优势明显，但却不利于对编队整体行为的控制。而虚拟结构编队飞行协同控制策略仅需要通过控制虚拟结构即可实现对整个编队控制的目的，易于对编队整体行为进行描述和控制［2－5］。文献［3－5］引入编队信息到虚拟结构的反馈提升了编队飞行的稳定性和鲁棒性。文献［4］中引入的多级虚拟结构分布式控制思想，使得每个虚拟结构中又包含有多个虚拟结构，有利于编队卫星的在轨扩充和撤离。然而，上述文献研究对象均集中于深空环境中的编队飞行，采用的卫星动力学模型为简单的二阶积分模型。而针对深空环境中编队卫星设计的控制器并不可简单地用于近地轨道编队卫星，需考虑地球引力、外界干扰甚至质量和转动惯量的不确定性对卫星位置和姿态的综合作用。因此，近地轨道空间中的虚拟结构编队飞行协同控制问题还有待于探讨和研究。

本文针对近地轨道编队飞行，考虑卫星质量和转动惯量的不确定性，分别对编队卫星和虚拟结构设计位置、姿态自适应协同控制器，同时证明了系统的稳定性和对有界扰动的抑制。最后，以编队整体平移和空间指向性偏转为例仿真验证了方法的有效性。

2 问题描述

2.1 轨道动力学模型

近地轨道卫星在地心惯性坐标系下的轨道动力学方程可以表示为［6］

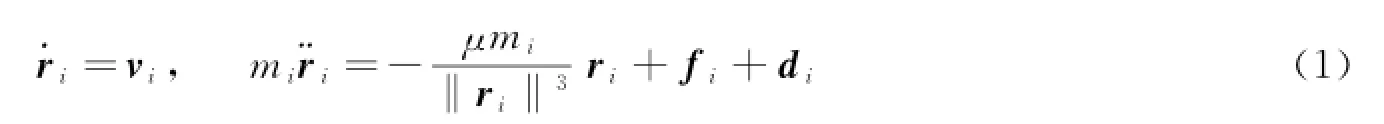
式中 mi为卫星i的质量；ri和vi为卫星i在地惯系中的位置；fi和di分别为卫星i所受的控制力和空间摄动力；μ为地球引力常数；‖ri‖表示向量ri的欧式范数。

2.2 姿态动力学模型

刚体卫星姿态动力学方程［6］为

式中 Ji为卫星i的转动惯量；ωi为卫星i相对于地惯系的角速度；τi和ti为卫星i所受的控制力矩和干扰力矩。

由单位四元数表示的卫星姿态运动学方程［7］为

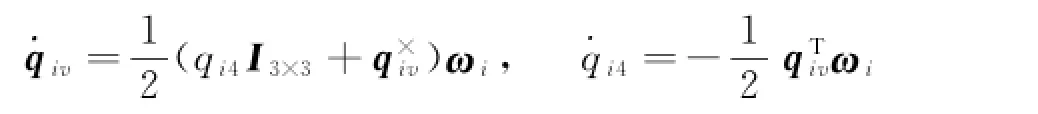
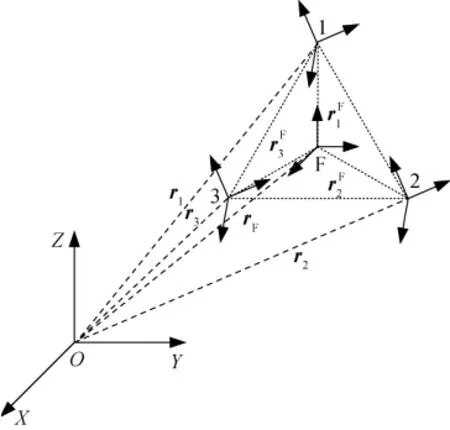
图1 虚拟结构模型示意Fig.1 Schematic diagram of virtual structure

2.3 虚拟结构模型

若将一颗卫星视为在惯性系中运动的刚体，则该刚体中各点的绝对位置会发生变化，但同一刚体中不同点之间的相对位置是一定的。若将该刚体中的某些点以卫星取代，且将刚体虚拟化后，则这些相对位置彼此固定的卫星便会组成一个形似刚体的卫星编队。如上所述，虚拟结构模型如图1所示：坐标系（O－XYZ）为地惯系；三角形的顶点代表三个编队成员，各成员本体系固联于成员质心；若将三星编队整体等同于一个虚拟刚体，并在虚拟质心处建立一个参考系F，F运动，则整个编队随之而动。

根据上述对虚拟结构模型的描述，结合科里奥利相对运动理论［8］，可得到由虚拟结构状态变量表示的编队成员期望状态表达式：

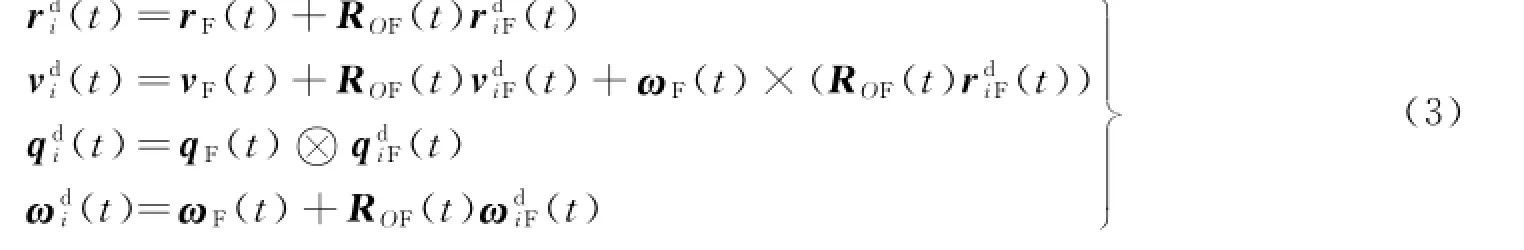
2.4 控制目标

假设卫星编队中各成员均可获取期望状态信息，定义卫星i的状态误差：位置误差速度误差，姿态四元数误差，角速度误差。其中，为四元数qi的逆，定义为；表示四元数乘法。控制目标为：在卫星质量和转动惯量不确定的条件下，对虚拟结构和卫星分别设计位置、姿态自适应协同控制器，控制虚拟结构状态向期望状态运动的同时，编队成员状态向期望状态运动，最终实现编队的整体控制。即t→∞时，

3 自适应协同控制器设计

在卫星编队飞行任务中，编队成员多为小卫星，其在轨运行过程中由于燃料消耗、弹性结构和太阳翼等造成的卫星质量和转动惯量不确定性不容忽视。因此，有必要设计自适应的协同控制器以使被控系统达到控制目标。

3.1 编队卫星位置和姿态自适应控制器设计

为便于控制器设计及后续定理的证明，定义位置和速度误差辅助变量（α为正常数）：

设计由PD控制律加上前馈自适应补偿环节组成的位置协同控制律如下：

式中 γi为正常数。定义卫星i的质量估计误差为，则有

暂不考虑卫星i所受的空间摄动力，系统状态误差动力学模型的闭环形式为

定理1 考虑被控系统动力学模型式（1），假设卫星i所受的空间摄动力di＝0，在卫星质量不确定的条件下，采用控制律式（6）和式（7），有及全局一致有界，且当t→∞时，满足→0，→0。

证明 选取如下Lyapunov函数：

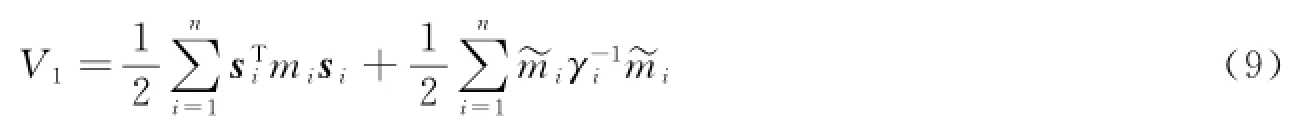
将式（9）沿被控系统式（1）对时间t求导，得

同样，引入有关姿态四元数和角速度误差的辅助变量β为正常数：

联立式（2）和式（11）可得：

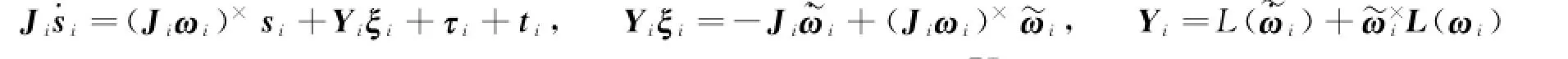
设计由PD控制律加上前馈自适应补偿环节组成的姿态协同控制律如下：

式中 ηi为正常数。定义ξi的估计误差为，则有

暂不考虑卫星i所受的干扰力矩，系统状态误差动力学模型的闭环形式为

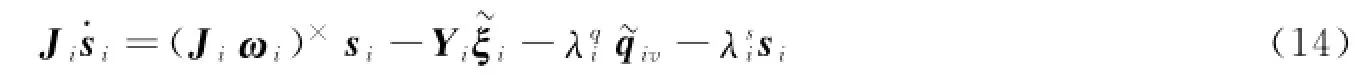
定理2 考虑被控系统动力学模型式（2），假设卫星i所受的干扰力矩ti＝0，在卫星转动惯量不确定的条件下，采用控制律式（12）和式（14），有，及全局一致有界，且当t→∞时，满足→0→0。

证明 选取如下Lyapunov函数［12］：

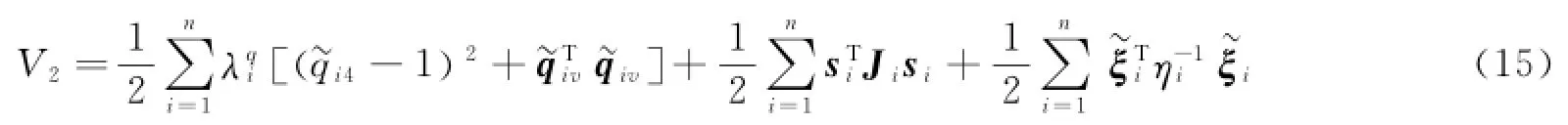
将式（15）沿被控系统式（2）对时间t求导，得：

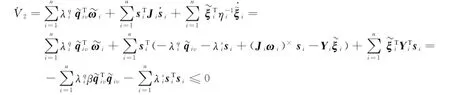
由于V1＞0，≤0，则（si，）∈L∞；结合式（11）和＝－，可得，及全局一致有界。另外根据式（12）～（14）可得∈L∞。由Barbalat引理可知，当t→∞时，si→0；而式（8）可视输入为si的一阶线性系统，则该系统是渐近稳定的，即，）∈L2∩L∞，因此，当t→∞时，有→0，→0。证毕。

3.2 有界扰动稳定性分析

下面对被控系统含有外部干扰的情况进行讨论。这里假设卫星i所受的空间摄动力Di和干扰力矩ti有界，即‖di‖≤Di，‖ti‖≤Ti，此假设合理且不失一般性。选取与式（9）和式（15）同样的Lyapunov函数，分别对时间t求导，得

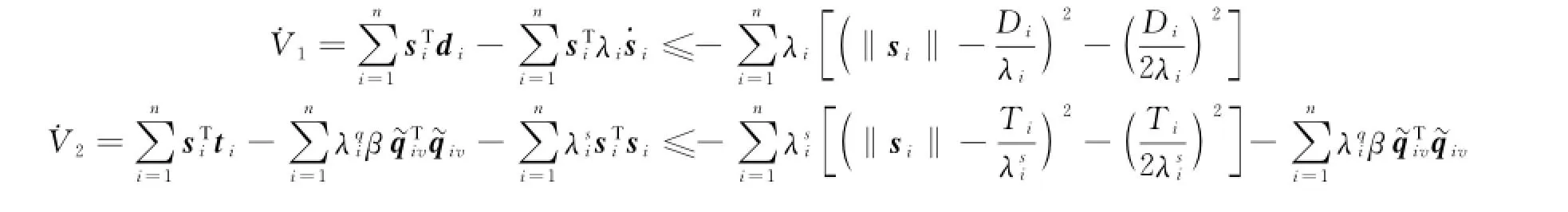
对于V1，对于V2，当时，有可见系统属于有界条件下的稳定，通过调节控制参数和，可使系统从任意初始状态收敛到平衡点的δi和εi邻域内。

3.3 虚拟结构位置和姿态控制器设计

在设计虚拟结构位置和姿态控制器时，须考虑编队信息至虚拟结构的反馈，以免虚拟结构运动过快导致编队卫星跟踪困难。定义编队信息变量：

将E1和E2分别引入虚拟结构的位置和姿态控制器中，设计位置和姿态控制律如下：

式中 λF、σF、、、ζF为正常数；其余参数的定义类似于卫星i，且不确定参数和的自适应更新律不变。当虚拟结构控制器中包含编队信息反馈时，卫星偏离期望状态，E1和E2增大，则控制器对虚拟结构的控制作用增强，从而实现对编队整体运动速度的控制。

系统的稳定性证明同上。

4 算例仿真与分析

下面以三星编队为例，对编队整体平移和空间指向性偏转控制进行仿真，验证本文控制方法的可行性和有效性。

4.1 编队整体平移控制仿真

仿真场景设定如下：假设虚拟结构初始状态为r（0）＝［0 10 0］Tm，q（0）＝［0 0 0 1］T，

FF现要求虚拟结构沿着空间直线x＝0.6t，y＝0.5t＋10，z＝0.3t运动，同时达到期望姿态四元数。要求编队卫星从具有一定误差的初始状态开始，跟踪虚拟结构，在参考系F中形成稳定的等边三角形，并在后续的运动中保持编队构型不变。

卫星在参考系F中的初始和期望位置：

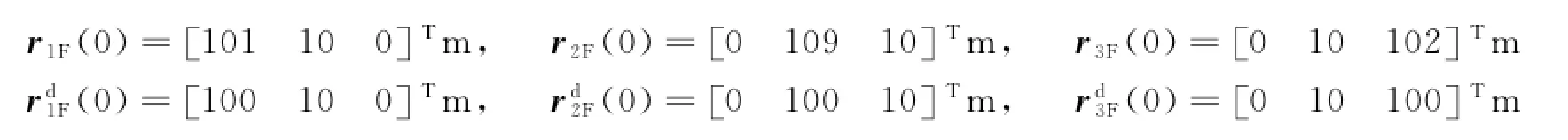
卫星在参考系F中的初始和期望姿态：

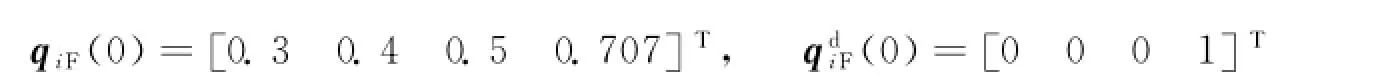
编队卫星整体平移协同控制的仿真曲线见图2～图5。从图2虚拟结构和编队卫星的位置跟踪误差曲线可以看出，虚拟结构位置跟踪误差收敛较快（约为10s），在其达到对期望轨迹的稳态跟踪后，各编队卫星才逐渐实现对各自期望轨迹的稳态跟踪。仿真结束时，编队卫星各方向位置跟踪误差可维持在较好的精度范围内。编队卫星在地惯系中的运动轨迹如图3所示，其中，A0，B0，C0分别为三颗卫星的初始位置，在仿真至70s时，三颗卫星建立起稳定的三角形构型△A1B1C1，并在后续的运动中维持构型不变直至仿真结束时的最终构型△A2B2C2。虚拟结构控制器中含编队信息反馈（σF＝1）和无编队信息反馈（σF＝0）时的位置跟踪误差对比如图4所示，其衡量指标δ为

可见，含编队信息反馈时，编队卫星具有更低的跟踪误差和更快的误差收敛速度。编队运动过程中虚拟结构和编队卫星姿态四元数矢量部分误差曲线如图5所示。类似于位置跟踪误差曲线，虚拟结构姿态四元数误差同样先于编队卫星收敛到零值附近，二者均具有较高的收敛精度。

图2 虚拟结构和卫星位置跟踪误差Fig.2 Position track errors of virtual structure and satellites

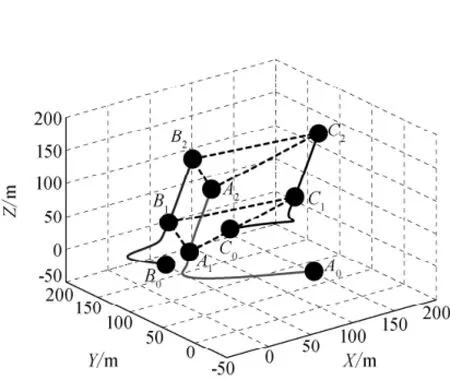
图3 编队整体平移运动轨迹Fig.3 Motion trajectories of formation satellites

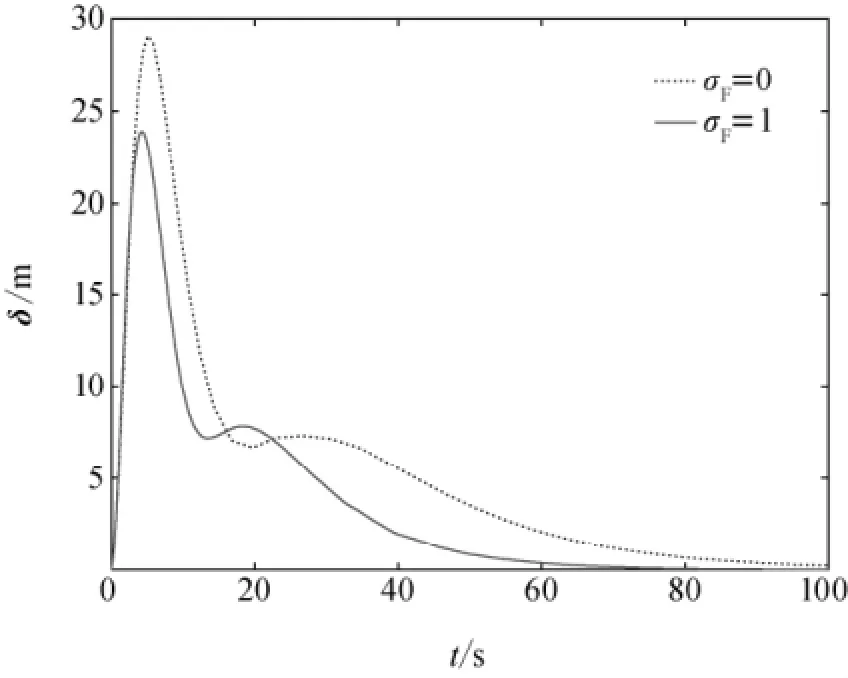
图4 σF＝1和σF＝0时位置跟踪误差对比Fig.4 Position track error when σF＝1andσF＝0

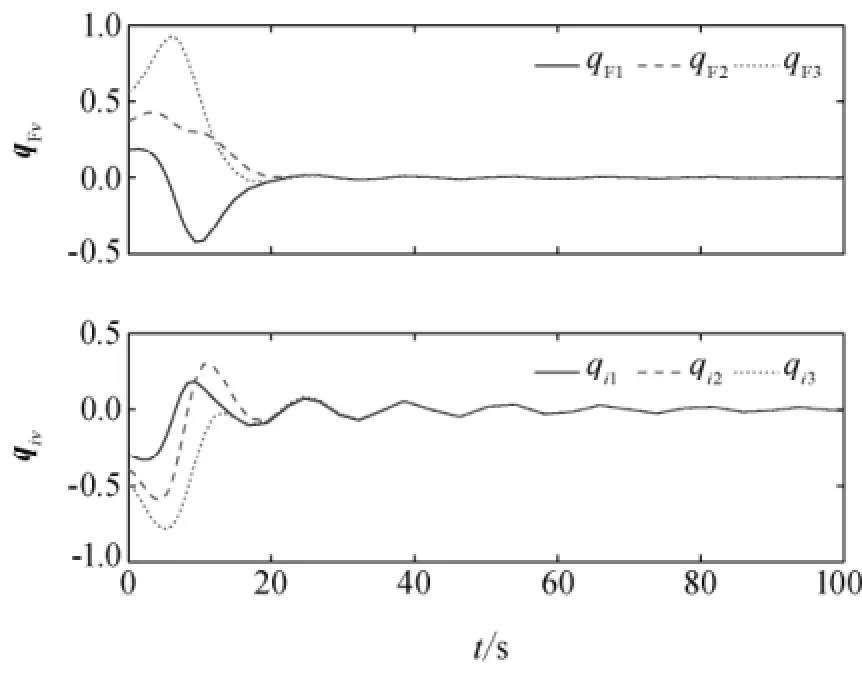
图5 虚拟结构和卫星姿态跟踪误差Fig.5 Attitude track errors of virtual structure and satellites attitude errors

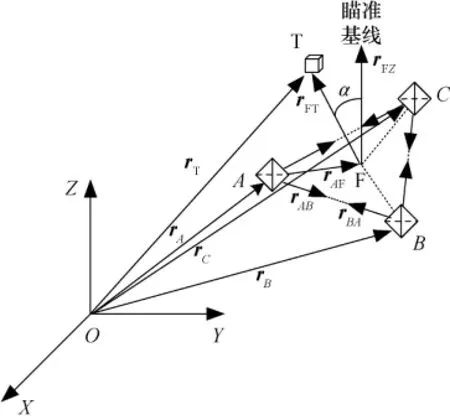
图6 编队空间指向性偏转示意Fig.6 Schematic diagram of formation directive declination

4.2 编队空间指向性偏转控制仿真

下面对编队在空间中的指向性偏转进行控制仿真，该技术主要用于实现对空间目标的跟踪和观测。仿真场景设定如下：如图6所示，锥体A、B和C分别代表三颗卫星，立方体T代表空间目标。初始时刻，三颗卫星组成一个平行于XOY平面的等边三角形，且具有相同的Z方向姿态指向。以△ABC的形心F为原点建立参考系F，垂直于三角形平面的向量rFZ为整个编队的瞄准基线。现要求整个编队在空间发生偏转，使得瞄准基线在一定时间t内转过α角最终指向空间目标T，正三角形构型保持不变，且实现各卫星姿态与瞄准基线的同步偏转。

若已知虚拟结构在地惯系中的初始状态变量、三颗卫星在参考系F中的初始状态变量及空间目标T在地惯系中的位置。要想实现编队整体对空间目标的指向，首先应确定编队瞄准基线rFZ从初始指向到最终指向空间目标T需要转过的α角。由三颗卫星在地惯系中的位置矢量（可通过上述两类初始状态变量计算得到），计算可得形心F在地惯系中的矢量：

进一步计算，可得编队瞄准基线rFZ在地惯系中的矢量：

式中 矢量rAF＝rF－rA；矢量rBF＝rF－rB。

由于空间目标T在地惯系中的位置已知，则有矢量rFT＝rT－rF，从而最终计算得到瞄准基线rFZ所需转过的α角：

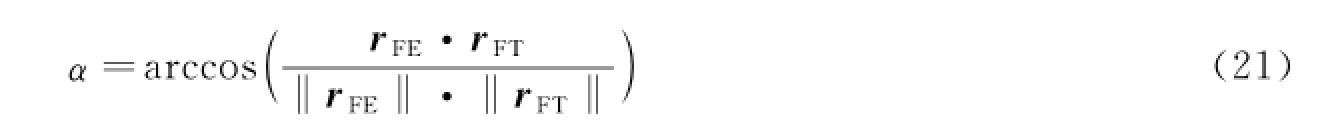
设置虚拟结构初始状态为rF（0）＝［8×106，8×106，8×106］Tm，qF（0）＝［0，0，0，1］Tm；三颗卫星在参考系F中的初始位置分别为r1F（0）＝［57.73，0，0］Tm，r2F（0）＝［－28.87，－50，0］Tm，r3F（0）＝［－28.87，50，0］Tm，即三颗卫星在参考系F中组成一个边长为100m的等边三角形，初始姿态均为qiF（0）＝［0，0，0，1］T；空间目标T在地惯系中的位置为rT＝［8×106－25，8×106＋20，8×106＋40］Tm。于是，由式（19）～式（21）计算可得编队瞄准基线rFZ所需转过的角α＝0.674 9rad。设定仿真时间t＝200s，编队卫星参数和控制器参数的取值同上。

编队在空间中针对目标T进行指向性偏转的三维仿真曲线如图7所示，可以看出，编队整体类似于一个刚体在空间发生偏转，并将瞄准基线rFZ最终指向空间目标T。三颗卫星的相对距离随时间t变化的曲线如图8所示，可见，整个偏转过程中三颗卫星可较好地保持相对距离，误差精度保持在0.006m范围内。三颗卫星的控制力和控制力矩变化曲线分别如图9和图10所示。由于卫星A和C在空间中的位置改变较大，故所需的控制力较大。而三颗卫星在空间中的姿态偏转一致，故所需的控制力矩相同。

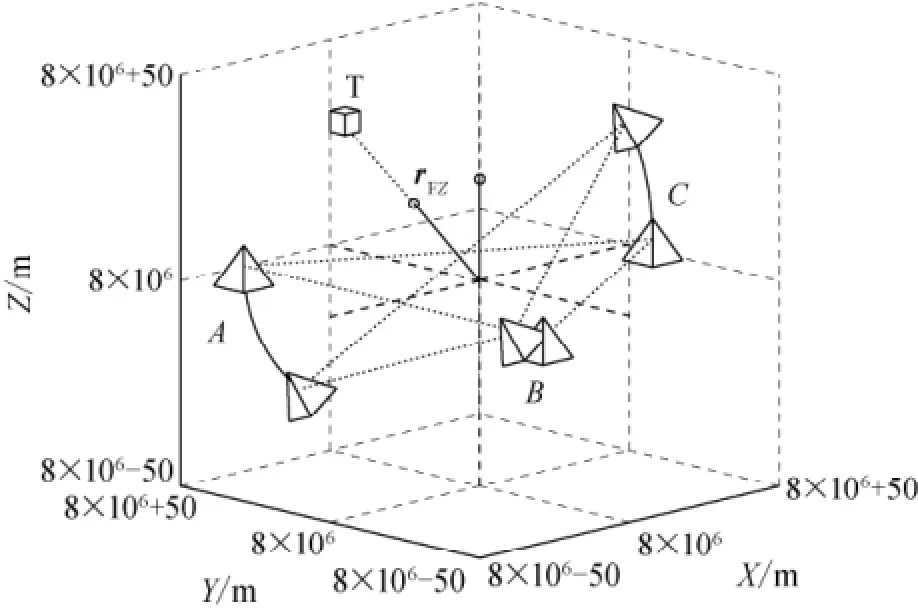
图7 编队空间指向性偏转三维仿真Fig.7 Simulation of formation directive declination

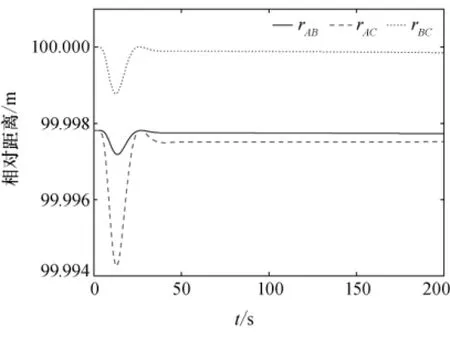
图8 编队卫星相对距离变化Fig.8 Relative distance between formation satellites

图9 编队卫星控制力变化Fig.9 Control force of formation satellites

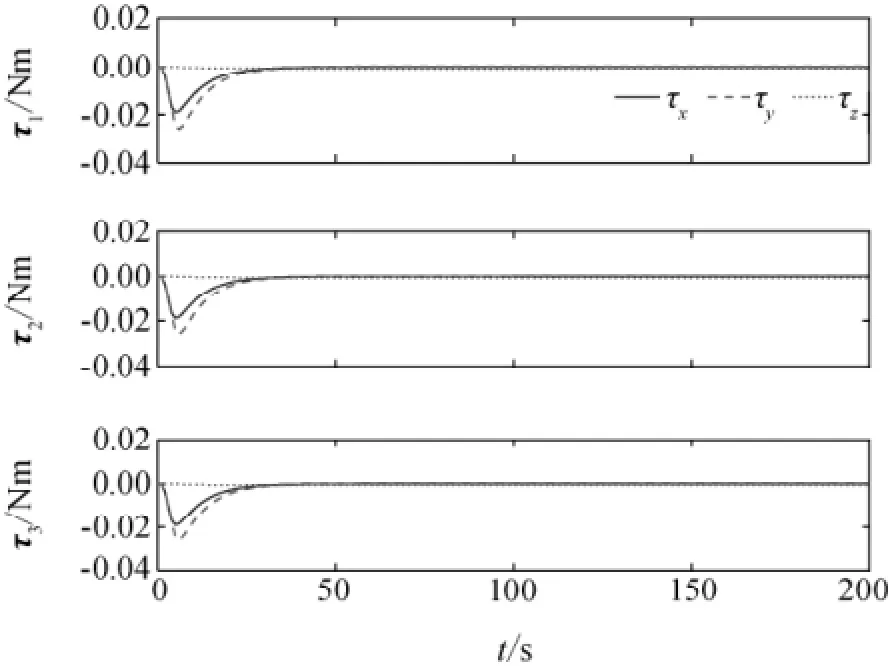
图10 编队卫星控制力矩变化Fig.10 Control torque of formation satellites

5 结束语

本文将虚拟结构引入近地轨道编队飞行的协同控制中，提出了一种基于虚拟结构的编队飞行自适应协同控制方法。考虑卫星质量和转动惯量的不确定性，分别对编队卫星和虚拟结构设计了一种独立的位置和姿态自适应协同控制器，且实现了编队信息至虚拟结构的反馈。最后，以编队整体平移和空间指向性偏转控制为例进行了仿真验证，可以得出以下结论：

1）设计的位置和姿态协同控制器可使编队在整体平移和空间指向性偏转过程中维持编队构型不变，验证了文中方法的有效性。

2）将编队信息引入到虚拟结构协同控制器，可有效改善编队卫星控制误差的收敛性能，并实现对编队整体运动速度的控制。

［1］ SCHARF D，HADAEGH F，PLOEN S.A survey of spacecraft formation flying guidance and control （part II）：control［C］∥Proceedings of the 2004 American Control Conference，Boston，June 30－July 2，2004，New Jersey：IEEE Press，2004.

［2］ BEARD R W，LAWTON J，HADAEGH F Y.A coordination architecture for spacecraft formation control［J］.IEEE Transactions on Control Systems Technology，2001，9（6）：777－790.

［3］ WEI R，BEARD R W.Virtual structure based spacecraft formation control with formation feedback［C］∥Proceedings of AIAA Guidance，Navigation，and Control Conference and Exhibit，Monterey，August 5－8，2002，Reston：AIAA Inc.，2002.

［4］ WEI R，BEARD R W.Decentralized scheme for spacecraft formation flying via the virtual structure approach［J］.Journal of Guidance，Control，and Dynamics，2004，27（1）：73－82.

［5］ 冯成涛，王惠南，刘海颖.基于虚拟结构的卫星编队机动控制 ［J］.系统工程与电子技术，2011，33（1）：143－145，156.

FENG CHENGTAO，WANG HUINAN，LIU HAIYING.Maneuver control of satellite formation based on virtual structure［J］.Systems Engineering and Electronics，2011，33（1）：143－145，156.

［6］ HOWARD D C.Orbital mechanics for engineering students［M］.London：Butterworth－Heinemann，2010：753－620.

［7］ 蒋锋，王惠南，皇超颂.基于对偶四元数的编队飞行卫星相对位姿描述［J］.中国空间科学技术，2012，32（3）：20－26，34.

JIANG FENG，WANG HUINAN，HUANG CHAOSONG.Algorithm for relative position and attitude of formation flying satellites based on dual quaternion［J］.Chinese Space Science and Technology，2012，32（3）：20－26，34.

［8］ 刘清华.科里奥利加速度的推导及物理分析［J］.邢台师范高专学报，2002，17（2）：39－41.

LIU QINGHUA.Deduction of Coriolis acceleration and its physical analysis［J］.Journal of Xingtai Senior Teachers College，2002，17（2）：39－41.

［9］ KHALIL H K.Nonlinear systems［M］.New Jersey：Prentice Hall，2002：323－329.

［10］ 张海博，胡庆雷，马广富.基于有向图的航天器编队鲁棒自适应姿态协同跟踪控制 ［J］.宇航学报，2012，33（8）：1072－1079.

ZHANG HAIBO，HU QINGLEI，MA GUANGFU.Robust adaptive cooperative tracking control for multi－spacecraft formation flying based on directed graph［J］.Journal of Astronautics，2012，33（8）：1072－1079.

［11］ VANDYKE M C，HALL C D.Decentralized coordinated attitude control within a formation of spacecraft［J］.Journal of Guidance，Control，and Dynamics，2006，29（5）：1101－1109.

［12］ 张保群，宋申民，陈兴林.输入受限的编队卫星分布式姿态协同控制 ［J］.中国空间科学技术，2011，31（1）：16－24，41.

ZHANG BAOQUN，SONG SHENMIN，CHEN XINGLIN.Decentralized attitude coordination control of satellites within formation under input constraints［J］.Chinese Space Science and Technology，2011，31（1）：16－24，41.

Adaptive Cooperative Control for Satellites Formation Flying Using Virtual Structure

HUANG Yong1LI Xiaojiang2，3YANG Yewei1LI Zhiliang1
（1 Department of Graduate Management，Equipment Academy of PLA，Beijing 101416）
（2 Department of Space Equipment，Equipment Academy of PLA，Beijing 101416）
（3State Key Laboratory of Laser Propulsion ＆Application，Equipment Academy of PLA，Beijing 101416）

Aiming at the cooperative control problem of satellites formation flying with mass，inertia uncertainties and external disturbances，an adaptive cooperative control method using virtual structure was proposed.Firstly，through the description of the virtual structure mode，the expressions between the virtual structure state variables and the desired states of the formation satellites were built.Secondly，the position and attitude adaptive cooperative controllers of the formation satellites and the virtual structure were designed.By introducing the state errors of the formation satellites to the virtual structure controllers，the feedback from the formation satellites to the virtual structure was realized.Besides，the closed－loop system stability and the controllers′bounded disturbances suppression were proved by using Barbalat lemma.Finally，the three－satellite formation cooperative maneuver and directive declination were simulated with the designed controllers.The results show that the designed controllers can adaptively estimate the satellite mass and inertial，and drive the control errors of the position and attitude to zero，which verify the method′s effectiveness.

Cooperative control；Adaptive；Virtual structure；Uncertainty；External disturbances；Satellites formation

10.3780／j.issn.1000－758X.2015.03.010

（编辑：车晓玲）

黄 勇 1986年生，2011年获空军航空大学军事装备学专业硕士学位，现为装备学院兵器科学与技术专业博士研究生。研究方向为分布式航天器协同控制。

2014－07－30。收修改稿日期：2014－10－07