考虑肋骨偏心的环肋圆柱壳弹性稳定性研究

邱昌贤，万正权

(中国船舶科学研究中心，江苏无锡214082)

考虑肋骨偏心的环肋圆柱壳弹性稳定性研究

邱昌贤，万正权

(中国船舶科学研究中心，江苏无锡214082)

摘要:采用2种满足简支边界条件的形函数，基于Ritz法建立环肋圆柱壳结构在静水外压下弹性失稳压力的直接计算方法，能区分肋骨的内外布置方式，且含有肋骨抗压刚度项，可推广至带有大肋骨的圆柱壳结构，或退化为无肋骨圆柱壳。分析表明，理论方法解和有限元结果较为一致，形式简单的3系数形函数具有较好的计算精度，内环肋圆柱壳的总体弹性稳定性比外环肋优越，大肋骨内置比外置更容易达到临界刚度，内、外肋骨圆柱壳的弹性局部失稳压力基本相当，忽略肋骨压缩应变能可使弹性总体失稳压力有所降低。

关键词:环肋圆柱壳;弹性稳定性;肋骨偏心;能量法

Elastic stability research of ring-stiffened cylindrical shell with rib eccentricity

QIU Chang-xian，WAN Zheng-quan
(China Ship Scientific Research Center，Wuxi 214082，China)

Abstract:Based on Ritz principle and 2 shape functions，a direct method has been built for calculating the critical elastic buckling of ring-stiffened cylindrical shell under external hydrostatic pressure．It could take the ring rib's radial eccentricity and compressive energy into account in buckling analysis，and be expanded for the calculating of cylindrical hull strengthened by heavy rib or without ribs．Theoretical solution agree with FEM results pretty well and the simpler function with 3 parameters has good precision．Calculation showed that cylindrical shell with internal ribs would have the advantage over externally ribbed ones in general elastic stability，and critical buckling stiffness of internal heavy rib is better than external ones．However，their local stability is almost the same．The general buckling pressure could be reduced as a result of the omission of ribs' compression．

Key words:ring-stiffened cylindrical shell; elastic stability，rib eccentricity;Rayleigh-Ritz

0　引言

环肋圆柱壳结构在外部静水压力下的稳定性问题一直得到国内外研究者的广泛关注，鉴于精确求解工作的难度和复杂性，工程上一般先求得弹性失稳压力，再对初始缺陷、几何非线性和材料塑性等影响因素进行半经验性修正［1－2］。但即使是理论模型较为简化的弹性稳定性，求解也很复杂，现有计算方法主要为基于能量原理的Rayleigh-Ritz法，用较容易求解的代数方程组代替微分方程，目前的规范公式是在此基础上略去能量式中的次要项，并进行简化而来。

现行规范不考虑环肋形心偏离圆柱壳中曲面的影响，弹性总体稳定性公式对内、外肋骨给出相同的计算结果［2］。对于带特大肋骨的舱段总体稳定性，由于理论基础相同，虽然大肋骨截面偏心距大得多，计算时也仅考虑了其计及带板的中和轴半径。对于通常被忽略的肋骨压缩应变能，戴自昶［3］导出了含肋骨抗压刚度项的环肋圆柱壳弹性总体稳定性方程，将肋骨面积平均分配到壳板上，以考虑肋骨

抗压刚度对临界压力的贡献，认为当总体失稳的周向整波数n≤5或mα1＞10时，肋骨压缩应变能的影响将不能忽略。本文由此出发，采用2种满足简支边界条件的形函数(3系数和5系数)，推导环肋圆柱壳结构的各能量表达式和水压做功计算式，最后建立一种通过求解系数矩阵特征值来获得结构在静水外压下的弹性失稳临界压力的直接计算方法。研究考虑肋骨偏心的弹性稳定性计算方法，计算无肋圆柱壳、内外T型环肋圆柱壳、采用大肋骨加强的圆柱壳长舱段结构的弹性失稳压力，并同规范解、有限元结果进行对比，分析肋骨内、外布置方式的影响，以及肋骨压缩应变能对总体失稳压力的影响。

1　考虑肋骨偏心的弹性稳定性计算方法

本文采用基于最小势能原理的Ritz法，借助2种不同的形函数并考虑肋骨偏心影响，对环肋圆柱壳结构能量表达式和水压做功进行推导，建立通过求解系数矩阵特征值来获得结构弹性失稳临界压力的计算方法和程序，并同有限元结果进行对比分析。

坐标原点取在舱壁或大肋骨处的圆柱壳中曲面上，x，y，z分别为纵向、周向和径向坐标，设u，v，w分别为纵向、周向和径向位移，径向坐标、挠度均以指向圆心为正。用能量法计算环肋圆柱壳的稳定性时，描述壳体失稳时的位移函数(屈曲波形)很重要，根据相关文献［2－4］，圆柱壳失稳时满足简支边界条件的第1种形函数取为:

式中: L为舱段计算长度; m为失稳时的纵向半波数; n为失稳的周向整波数，A，B，C为常系数。

圆柱壳简化为平面应力状态并仅考虑小挠度，由薄壳理论中的Kirchoff平断面和直法线假设得到γxz=γyz= 0;同时认为圆柱壳板处于平面应力状态，因此法向应力σz= 0，经代入化简得到:

式中: V1和V2分别为圆柱壳板的弯曲和中面应变能，积分后得到的具体形式与文献［2］相同，在此不赘述。

计算肋骨应变能时，引入以下基本假设: 1)环肋横截面形状在变形中保持不变; 2)环肋近似为单向应力状态; 3)环肋与壳板在连接处保持变形协调; 4)环肋的拉伸与弯曲变形符合叠加原理; 5)环肋的扭转和面外弯曲可忽略。

考虑肋骨偏心的影响，设环肋的横截面积为F，截面形心的径向坐标为ef(内肋骨ef＞0，外肋骨ef＜0)，则其中和轴半径为R－ef，近似认为肋骨处于单向应力状态，则σx=0，σz=0，γxz=γyz=0。将肋骨视为壳板的一部分，取其位移函数(形函数)与圆柱壳板相同，则肋骨截面任一点的周向应变为:

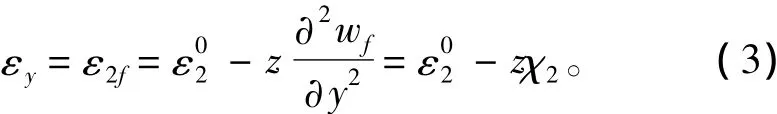
整个舱段内有nf= (L/l)－1根肋骨，对距离坐标原点x= i×l处的第i根肋骨，考虑肋骨截面偏心及扭转时其应变能Vfi可按下式计算:

式中: Hi(x)为第i根环肋的应变能环向密度，由于Hi(x)与径向坐标z无关，且当环向坐标y变化时保持不变，因此可证明积分时仅需取dy= (R－yci) dφ; yci为第i根环肋计及带板宽度为l的组合截面形心的径向坐标; Rfi为第i根环肋计及带板宽度为l的组合截面形心的半径，Rfi= R－yci。

对于被文献［2－4］等忽略的肋骨压缩应变能，本文引入系数k2=1或0以分析其对环肋圆柱壳弹性失稳压力的影响。肋骨截面的扭转、翘曲和面外弯曲的应变能则在计算中予以忽略。

式中: Ii为第i根环肋计及带板宽度为l的组合截面的惯性矩; I0i为第i根环肋自身惯性矩; Fi为肋骨横剖面面积; y0i为肋骨横剖面中和轴到壳板表面的距离，y0i+ 0.5t= efi。

假设失稳前环肋圆柱壳在静水外压作用下为无矩应力状态，忽略肋骨对周向中面应力的影响，则横剖面与纵剖面上的膜应力为: T1=－PR/2，T2=－PR，基于此简化分别计算纵向力与横向力做功，再结合前面求得的结构各部分能量，即可建立能量平衡方程，为简化表达式，式中引入参数α=πR/L。

根据能量原理，结构总能量П取极小值的条件是П对A，B，C的偏微分为0，对于同材料、等间距布置且截面相同的nf根肋骨，得到如下齐次线性方程:

此方程组存在非零解的充要条件是系数矩阵行列式为0，这个矩阵是对称的，cij= cji。

展开行列式并整理后得到一元一次方程，其根即为结构弹性失稳的临界压力值。

此外，本文计算时还采用Kendrick的5系数形函数［1，5］，A1，B1，C1所在项代表总体屈曲波形，B2，C2所在项代表肋间壳板局部屈曲波形。

在此基础上推导能量表达式的过程与3系数形函数类似，只是形式更为繁琐，当得到的5阶系数矩阵行列式为0时，线性齐次方程组存在非零解，此系数矩阵对称，aij= aji。

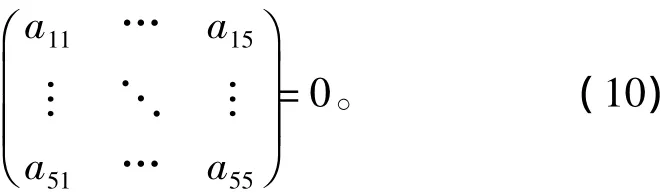
展开行列式并整理后得到一个一元二次方程，2个实根中的最小值即为和弹性失稳时各纵向半波数m和周向整波数n对应的临界压力。

2　计算结果对比分析

基于前述理论方法编制程序，对无肋骨圆柱壳、内外T型环肋圆柱壳、含大肋骨的环肋圆柱壳结构在静水外压下的弹性稳定性展开计算，并进行有限元分析和对比。

计算模型的主要结构参数为: u =1.15;β= 2.87;圆柱壳半径、厚度比R/t =107;长度、直径比L/D=1.38和2.77;大肋骨与普通肋骨惯性矩比Ihf/If=16，39.06和81。肋骨均为等间距布置，分为16跨和32跨。

有限元模型均采用4节点板壳单元shell181划分为映射网格，在两端边界按简支约束径向线位移，在中部的壳板对称面上约束纵向刚体位移。计算取材料的弹性模量E =1.96×105MPa;泊松比μ=0.3。

图1　无肋圆柱壳弹性失稳压力计算结果对比(m =1，2，3)Fig.1　Results comparison of different methods for elastic stability of cylindrical shell without ribs (m =1，2，3)

2.1无肋骨圆柱壳结构的弹性稳定性

对于无肋骨圆柱壳结构的弹性稳定性，理论方法得到的解与对应的有限元结果(m，n均相等)十分吻合，如图1所示，有限元分析得到的部分弹性失稳波

形如图2所示，采用不同形函数的2种理论方法所得结果差别很小，5系数形函数对应的临界压力略低。

图2　无肋圆柱壳结构弹性稳定性有限元计算结果(m=1，n =5)Fig.2　FEM results for elastic stability of cylindrical shell without ribs (m =1，n =5)

2.2内、外T型环肋圆柱壳结构的弹性稳定性

针对内肋骨和外肋骨2种形式，利用本文方法、规范方法和有限元法计算环肋圆柱壳总体和局部弹性稳定性，如表1所示。圆柱壳L/D = 1.38，内、外肋骨的截面参数完全一样。

本文方法与有限元结果比较一致，临界压力最低的总体弹性失稳形状都是纵向一个半波、周向三个整波，且计算均表明内肋骨圆柱壳的总体弹性稳定性高于外肋骨，增幅约20%。2种不同形函数的结果相比，形式简单的3系数形函数具有较好的计算精度，5系数形函数对应的临界压力较低一些。规范为提高实用性忽略了肋骨压缩应变能，算例表明，忽略肋骨压缩应变能后总体失稳压力有所降低。

由于局部失稳时肋骨按简支边界处理，不考虑肋骨的影响，因此本文方法的局部失稳压力计算值和规范结果相当一致，且不能区分内、外肋骨的影响。有限元结果比理论解高一些，周向波数n则略低，从失稳波形云图(图3～图4)可看出，肋骨也参与了壳板的局部失稳，有限元分析表明，内肋骨圆柱壳的局部弹性稳定性与外肋骨基本相当，在算例中，内肋骨圆柱壳的局部失稳压力比外肋骨仅提高1.9%。

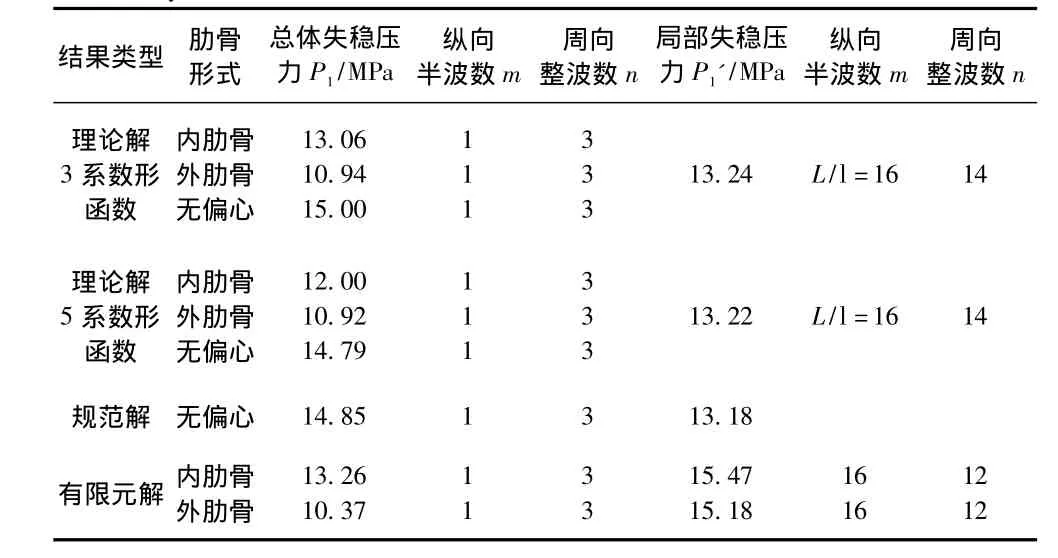
表1　静水外压下内、外肋骨环肋圆柱壳弹性稳定性计算结果对比Tab.1　Results comparison of different methods for elastic stability o cylindrical shell with internal or external ribs

表2　肋骨压缩应变能对环肋圆柱壳总体弹性失稳压力(MPa)的影响Tab.2　The influence of ribs' compression energy on general elastic stability (MPa) of cylindrical shell

图3　环肋圆柱壳结构(外肋骨)总体弹性失稳波形(m =1，n =3)Fig.3　FEM results for elastic general buckling shapes ofcylindrical shell with external ribs (m =1，n =3)

图4　环肋圆柱壳舱段结构(外肋骨)局部弹性失稳波形(m =16，n =12)Fig.4　FEM results for elastic local buckling shapes of cylindrical shell with external ribs (m =16，n =12)

2.3含大肋骨环肋圆柱壳结构的弹性稳定性

对于中部采用大肋骨加强的环肋圆柱壳长舱段结构，利用本文方法、规范方法和有限元法计算了总体弹性稳定性，如表3所示。圆柱壳L/D =2.77，大肋骨与普通肋骨惯性矩比Ihf/If=1，16，39.06和81。

无大肋骨时，圆柱壳加长后结构总体弹性稳定性迅速下降，长度增加1倍，临界压力下降近50%。为提高总体失稳压力，在中部设置大肋骨并逐步提高其惯性矩，发现内大肋骨圆柱壳的总体弹性稳定性比外大肋骨好，在截面尺寸相同的情况下，大肋骨内置比外置时先达到临界刚度:即大肋骨能保持正圆形，阻隔总体失稳波形沿纵向蔓延。当大肋骨低于临界刚度时，圆柱壳将连大肋骨在内发生失稳，临界状态的总体弹性失稳形状都是纵向一个半波、周向2个整波;当大肋骨高于临界刚度时，失稳发生在大肋骨之间的圆柱壳上，临界状态的总体弹性失稳形状都是纵向一个半波、周向3个整波。

规范方法得到的结果偏高，且内、外大肋骨的差异较小，在用于确定大肋骨临界刚度时可能偏危险。2种不同形函数的计算结果相比，5系数形函数对应的临界压力偏低一些，随着大肋骨腹板增高，尺寸加大，理论解与有限元结果的偏差有所提高。

表3　静水外压下带大肋骨的环肋圆柱壳总体弹性稳定性计算结果对比Tab.3　Results comparison of different methods for general elastic stability of cylindrical shell with heavy ribs

图5　带大肋骨的环肋圆柱壳结构(外肋骨)总体弹性失稳波形(m =1，n =2)Fig.5　FEM results for elastic general buckling shapes of cylindrical shell with external heavy ribs (m =1，n =2)

图6　带大肋骨的环肋圆柱壳结构(内肋骨)总体弹性失稳波形(m =1，n =3)Fig.6　FEM results for elastic general buckling shapes of cylindrical shell with internal heavy ribs (m =1，n =3)

3　结语

本文考虑肋骨偏心影响，采用了2种满足简支边界条件的形函数，基于Ritz法建立了一种通过求解矩阵特征值来获得环肋圆柱壳结构在静水外压下弹性失稳压力的计算方法，含有肋骨抗压刚度项，既能区分肋骨的内外布置方式，又可推广至带有大肋骨的圆柱壳结构，或退化为无肋骨的圆柱壳，方法的适应性较好。本文对无肋圆柱壳、环肋圆柱壳及带大肋骨的圆柱壳结构的弹性稳定性进行分析，并采用较为简洁的规范公式进行对比计算，同时也在Ansys中进行有限元弹性屈曲分析，直接获得失稳临界压力及波形特征，通过对比，分析了肋骨内、外布置方式和肋骨抗压刚度的影响。主要结论如下:

1)对于无肋骨圆柱壳结构的弹性稳定性，理论方法解与对应的有限元结果(m，n均相等)十分吻合，采用不同形函数的2种理论方法所得结果差别很小，5系数形函数对应的临界压力略低。

2)在考虑肋骨偏心计算环肋圆柱壳的弹性稳定性时，本文方法与有限元结果较一致，且内肋骨圆柱壳的总体弹性稳定性高于外肋骨，算例表明增幅约20%，且忽略肋骨压缩应变能后总体失稳压力有所降低。2种不同形函数的结果相比，形式简单的3系数形函数具有较好的计算精度，5系数形函数对应的临界压力更低一些。

3)本文给出的局部稳定性计算值和规范结果基本一致，且不能区分内、外肋骨的影响。有限元结果比理论解高一些，波形特征也略有差别，内、外肋骨圆柱壳的局部弹性失稳压力相当，内肋略高。

4)无大肋骨时，圆柱壳加长后结构总体弹性稳定性迅速下降，在中部设置大肋骨并逐步提高其惯性矩后发现，内大肋骨圆柱壳的总体弹性稳定性比外大肋骨好，在截面尺寸相同的情况下，大肋骨内置比外置时先达到临界刚度。当大肋骨低于临界刚度时，圆柱壳将连大肋骨在内发生失稳;当大肋骨高于临界刚度时，失稳发生在大肋骨之间的圆柱壳上。

5)对带大肋骨的圆柱壳，规范方法得到的结果偏高，且内、外大肋骨的差异较小，在用于确定大肋骨弹性临界刚度时的适应性欠佳。2种不同形函数的计算结果相比，5系数形函数对应的临界压力偏低一些，随着大肋骨腹板增高，尺寸加大，理论解与有限元结果的偏差有所提高。

参考文献:

［1］周承倜．薄壳弹塑性稳定性理论［M］．北京:国防工业出版社，1979．

［2］潜艇结构设计计算方法GJB/Z 21A－2001［S］．国防科学技术工业委员会，2001:5－13．Methods for design and calculation of submarine structure．GJB/Z 21A－2001［S］．National Defense Science＆Technology Industry Committee，2001:5－13．

［3］周承倜．弹性稳定理论［M］．成都:四川人民出版社，1981．

［4］许辑平．潜艇强度［M］．北京:国防工业出版社，1985．

［5］陈雅菊．环肋圆柱壳稳定性分析［J］．舰船科学技术，2000，22(4) :14－24．CHEN Ya-ju．Stability analysis for ring-stiffened cylindrical shell［J］．Ship Science and Technology，2000，22(4) : 14 －24．

［6］唐家祥，王仕统，裴若娟．结构稳定理论［M］．北京:中国铁道出版社，1989:47－54．

［7］戴自昶．环肋圆柱壳总稳定性探讨［J］．舰船科学技术，2000，22(4) :2－9．

［8］李国栋，尚新春．考虑剪切效应的环肋圆柱壳的稳定性［J］．工程力学，2007，24(9) :43－48．

［9］胡勇，马建军，张政，等．考虑筋/板相互作用的环肋圆柱壳屈曲强度分析［J］．船舶力学，2005，9(4)．

［10］周素莲，聂武，彭懿．单壳体潜艇结构损伤后的屈曲分析［J］．哈尔滨工程大学学报，2010，31(9)．

作者简介:邱昌贤(1981－)，男，高级工程师，研究方向为水下工程结构理论与试验。

收稿日期:2014－09－11;修回日期: 2014－11－13

文章编号:1672－7649(2015) 07－0014－06doi:10.3404/j.issn.1672－7649.2015.07.004

中图分类号:U674．76

文献标识码:A